1. Introduction
In the realm of modern physics and chemistry, there is a significant focus on comprehending and predicting the behavior of molecular systems. The study of interactions and motions among multiple particles, such as the three-body problem and more general N-body problems, has long captivated theoretical and computational physicists[1-7]. While traditional analytical methods are effective for two-particle interactions, they become less viable as the number of particles increases, often rendering analytical solutions difficult or impossible to obtain. In such scenarios, numerical simulation becomes essential for exploring complex system dynamics. Molecular dynamics (MD) simulation stands out due to its powerful computational capabilities and direct representation of physical processes; it has become an ideal choice for studying molecular motion[2]. By recording extensive data during simulations and utilizing statistical analysis techniques along with data visualization tools, key dynamic features and patterns can be extracted from molecular systems. Specifically using the Moldy program for MD simulations records information on molecules' position, velocity, and energy under various conditions which is then used to create graphical representations illustrating dynamic changes in the system[1]. Additionally enhancing our understanding of molecular motion involves converting simulation results into vivid 3D animations using visual molecular dynamics software (VMD), allowing an intuitive display of instantaneous characteristics of molecular trajectories and interactions[5]. The primary aim here is to demonstrate how Moldy and VMD software effectively solve complex multi-body problems while revealing intrinsic dynamic laws governing molecular systems. This work not only provides profound insights into molecular motion but also highlights the crucial role played by modern computational tools in advancing fundamental scientific research across fields like chemistry biophysics materials science.
2. Reasons why the three-body problem cannot be solved
The challenge posed by the three-body problem has persisted in physics since Newton's era, owing to its inherently non-linear dynamics[8]. This feature engenders a system that is both unpredictable and highly sensitive to initial conditions, embodying what we now recognize as chaotic behavior[9][10]. A minute alteration in the starting positions, velocities, or directions of the three interacting bodies can precipitate erratic outcomes, rendering the system's evolution chaotic. Contrary to the two-body scenario, where the principles of energy and angular momentum conservation yield exact analytical solutions, the simplicity of formulation does not translate into solvability for the three-body problem. This was acknowledged by the Swedish mathematician Gosta Mittag-Leffler in the latter part of the 19th century, who identified that a universal, closed-form resolution eludes us[11]. While an overarching analytical answer remains elusive, the advent of sophisticated numerical techniques coupled with computational simulations has enabled insights and predictive capabilities within certain constraints[12]. These methodologies, however, are typically confined to short-term predictions and the analysis of particular initial states, falling short when faced with the uncertainties inherent in long-term projections. In essence, the three-body problem highlights the limitations of deterministic physics when confronted with complex systems, demonstrating the boundaries of predictability and the onset of chaos. Numerical approaches and simulations provide a window into understanding specific instances, but they do not offer a panacea for the intrinsic unpredictability over extended periods[13][14].
3. Difficulty in predicting molecular motion
Forecasting the detailed paths and dynamic characteristics of molecular movements stands as a pivotal hurdle within the realms of chemistry, biophysical studies, and material sciences. This complexity arises fundamentally from the intricate web of interactions across multiple scales within molecular systems, entangled further by quantum phenomena[15]. Atoms, being the building blocks of molecules, engage in interactions governed by principles of both classical mechanics and quantum mechanics—especially critical when addressing electron dynamics and bond formations. The inherent uncertainty principle of quantum mechanics dictates that, at the microcosmic scale, it is impossible to simultaneously measure a particle's location and momentum with precision. This presents a significant obstacle to predicting molecular motion in scientific research.Moreover, the vast range of temporal and spatial scales involved in molecular dynamics—from electron vibrations occurring in femtoseconds 10^-15 seconds to the conformational shifts of biomacromolecules spanning micrometers—poses significant challenges. This multi-scale characteristic necessitates models capable of accurately depicting molecular behaviors across diverse dimensions, often transcending the capabilities of singular theoretical frameworks or computational strategies. The molecular landscape is characterized by multifaceted interactions encompassing van der Waals forces, hydrogen bonding, electrostatic interactions, and hydrophobic effects. These interactions demonstrate rapid changes in strength and orientation as intermolecular distances fluctuate, resulting in a system that exhibits pronounced nonlinearity.This sensitivity to initial conditions, manifesting as chaotic behavior, ensures that minute variances at the outset can precipitate dramatically divergent outcomes over extended durations, amplifying the intricacies associated with long-term predictions. Furthermore, computational resource constraints significantly impinge upon the ability to precisely forecast molecular motions. The computational demands of molecular dynamics simulations, involving extensive differential equation solving, require exceptional processing power and data storage capabilities. Despite notable advancements in high-performance computing and algorithmic enhancements in recent times, achieving comprehensive quantum mechanical-level simulations for sizable molecular ensembles, comprising thousands to millions of atoms, remains a formidable challenge. In essence, predicting molecular motion calls for a nuanced understanding of interactions across scales, a robust computational infrastructure, and innovative methodologies that can navigate the complexities inherent in molecular systems, all of which collectively define the frontiers of scientific inquiry in this domain.
4. Using a computer program to simulate molecule movement and draw experimental images
In our investigation, we employed the Moldy molecular dynamics software to explore the microscopic dynamics of argon molecules under specified environmental conditions. Moldy was chosen for its proficiency in managing complex dynamics and its reliability in simulating the interactions among a multitude of particles. Our simulation parameters were calibrated to a temperature of 84 Kelvin at average and standard atmospheric pressure, mirroring near-real-world molecular activity.
For a precise portrayal of intermolecular forces, we utilized the OPLS-AA force field[16]. The simulation was conducted within a cubic framework of 10 nanometers on each side, populated with over 100,000 particles, ensuring statistical relevance while keeping computational demands feasible. Periodic boundary conditions were applied to mitigate edge effects and procure more authentic molecular dynamics[17].
Data acquisition commenced during the initial equilibration phase and proceeded for a duration of 10 nanoseconds, with data snapshots taken every picosecond. This approach allowed for the capture of transient molecular positions and velocities. Using Moldy's integrated analysis tools, we were able to extract crucial metrics such as the mean free path and hydrogen bond formation rates.
Post-simulation, we harnessed various graphical representation techniques to translate the raw data into comprehensible visual formats. Utilizing Gnuplot, we plotted the temporal evolution of molecular energies, offering insights into the system’s stability and energy fluctuations. We verify the conservation of energy by simultaneously showing the various energy changes in the movement of argon molecules in Figure 1. By analyzing the data in Figure 2, we can conclude that the confidence interval of the mean kinetic energy of the water molecule does not exactly coincide with its overall fluctuation. According to Figure 3, we successfully verified that temperature is directly proportional to the kinetic energy of the molecules in motion.
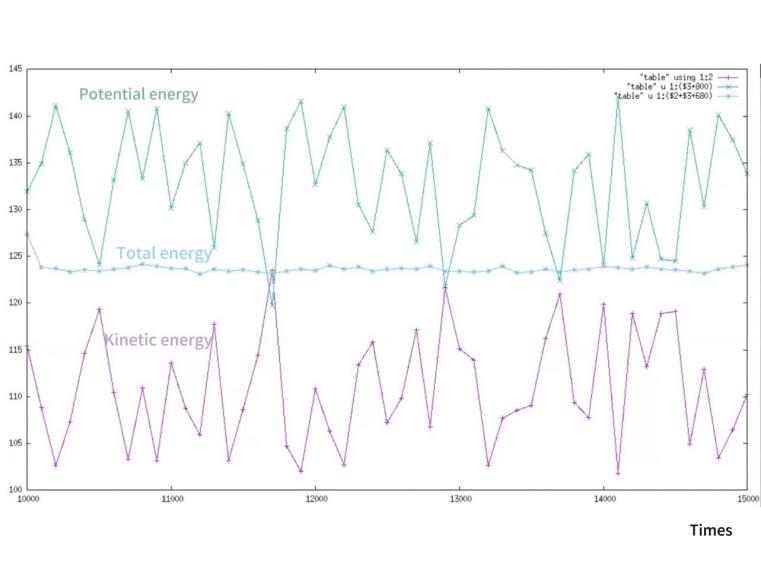
Figure 1. Changes in kinetic energy, potential energy, and total energy of argon molecules when they move
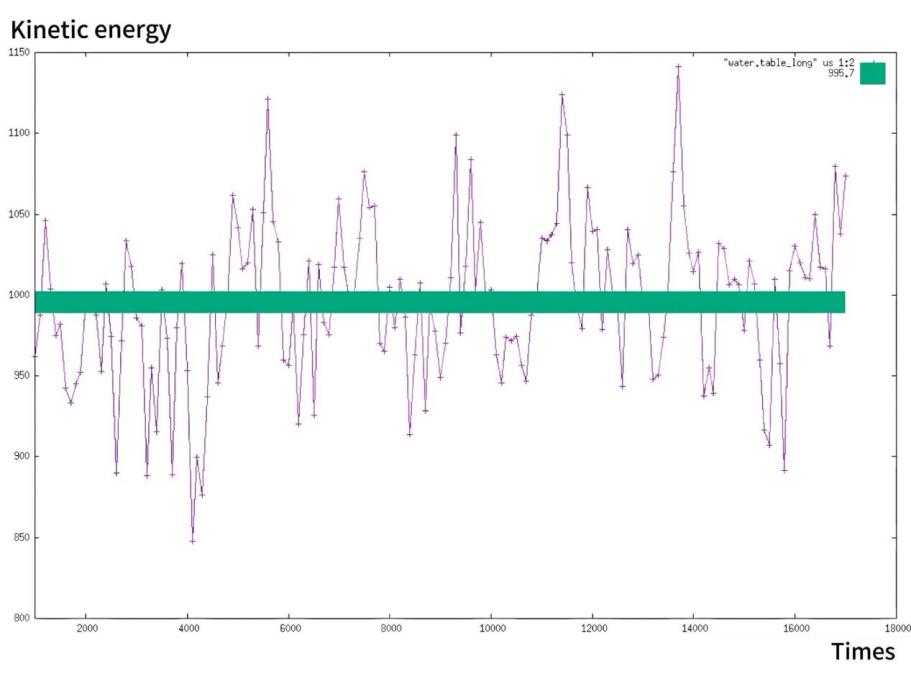
Figure 2. Fluctuation of the kinetic energy in water molecules when they move
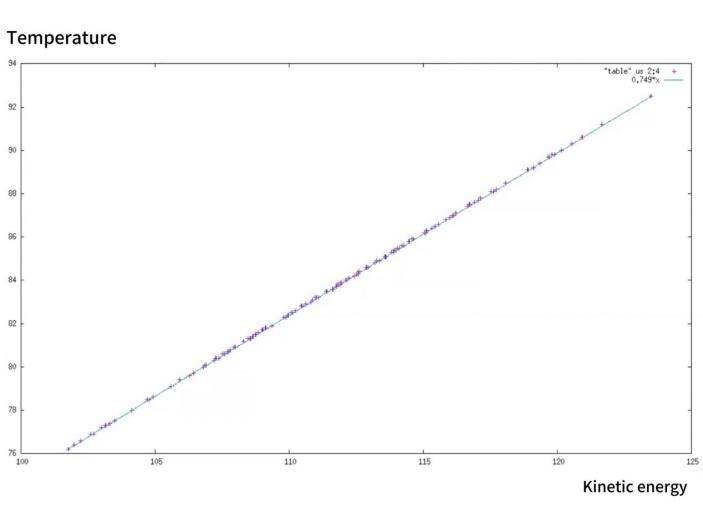
Figure 3. The graph showing the relationship between temperature and kinetic energy when argon molecules move
Significantly, we leveraged VMD (Visual Molecular Dynamics) software to animate the simulation trajectories, converting them into three-dimensional visualizations. These animations vividly depicted the molecular motions and interactions, providing a visual narrative of the simulation’s findings. Moreover, static images generated by VMD served as valuable aids in interpreting the simulation data. According to the two sets of pictures below, it is evident that the arrangement of molecules is progressively becoming disordered. In particular, through the analysis of Figure 4 to figure 7, We investigated the interaction of hydrogen bonds between water molecules during their motion, resulting in a significant reorganization of water molecules within the cube
.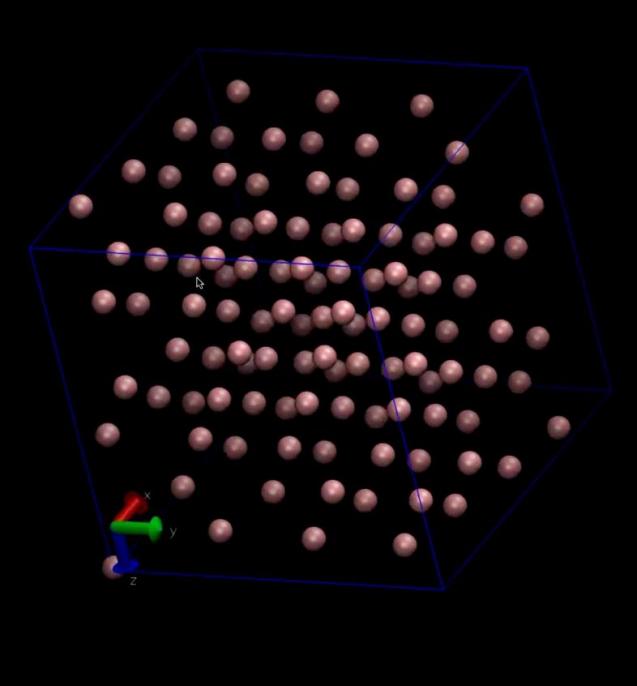
Figure 4. The image of argon molecules before the simulation
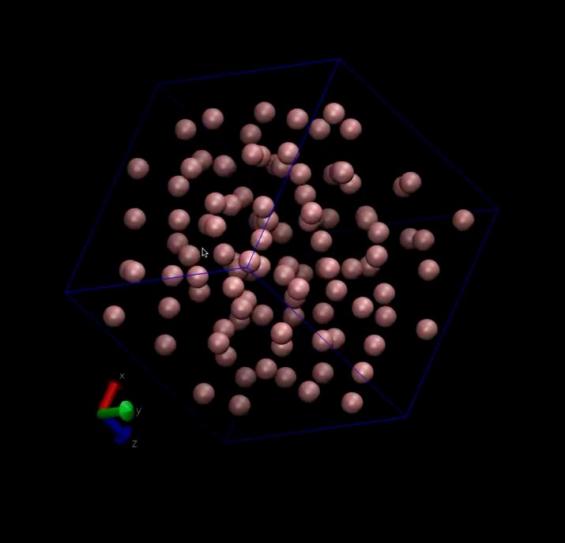
Figure 5. The image of argon molecules after simulation

Figure 6. The image of water molecules before simulation
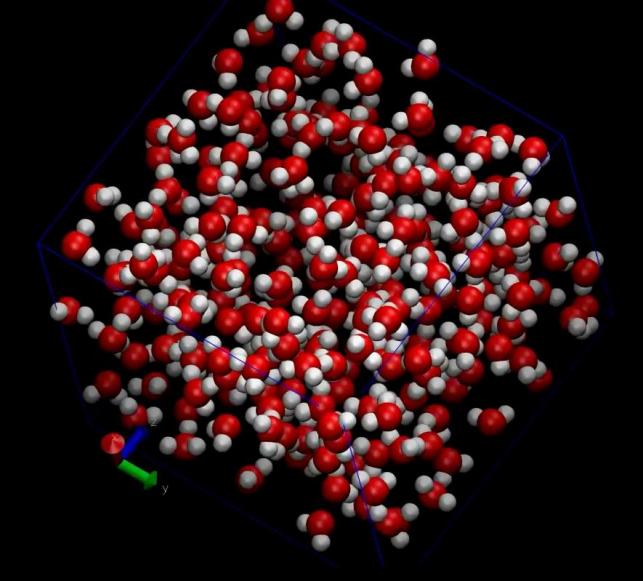
Figure 7. The image of water molecules after simulation
These visualizations and analyses not only underscored the validity of our simulation setup but also laid the groundwork for further theoretical exploration and hypothesis testing.
By employing a combination of advanced simulation software, rigorous data analysis, and powerful visualization tools, we were able to delve into the intricate dynamics, yielding insights that align with empirical observations and theoretical predictions.
5. Conclusion
Through leveraging the Moldy program to simulate the dynamics within intricate molecular constellations, this investigation has made significant strides in addressing the complexities inherent in multi-body dynamics, notably tackling the three-body dilemma and extending to broader N-body configurations. Our simulations have not only captured the ephemeral interactions between molecules but also illuminated the enduring patterns of stability they manifest under varied environmental conditions. By meticulously crafting our experimental methodology, we have amassed comprehensive datasets chronicling molecular trajectories, energy statuses, and the nuances of interaction intensities and frequencies, furnishing a robust foundation for exhaustive scrutiny. Harnessing the potent computational prowess of the Moldy program, we have simulated a spectrum of elaborate chemical reactions and physical phenomena at the subatomic and molecular scales. This has shed new light on foundational aspects within biological systems, materials science, and chemical engineering, offering fresh insights and perspectives. A standout feature of our study is the visualization of simulation outcomes. Employing VMD software, we have transmuted abstruse simulation data into captivating three-dimensional animations and interactive visual models. These visual representations not only augment the comprehensibility of the data but also afford lay readers an intuitive grasp of the convoluted nature of molecular motion and its repercussions on macroscopic attributes. Our findings affirm that the Moldy program, when synergized with VMD's visualization capabilities, constitutes an optimal toolkit for probing molecular motion within multibody settings. Via these methodologies, we have been privy to observations that had hitherto evaded detection, encompassing the collision frequencies between molecules, pathways of energy dissemination, and the intricate dynamics of structural metamorphoses. These revelations bear profound implications for the refinement of pharmaceutical design, enhancement of material characteristics, and an enriched comprehension of life's fundamental processes. Prospectively, we intend to escalate the scale of our simulations to probe molecular dynamics within expansive systems, concurrently integrating machine learning paradigms to forecast and dissect molecular conduct under a more extensive array of circumstances. We are confident that ongoing technological breakthroughs and cross-disciplinary partnerships will perpetually propel the discipline of molecular dynamics simulation forward, unveiling novel avenues to unravel the intricate puzzles in biology, chemistry, and physics.
References
[1]. Alder, B. J., & Wainwright, T. E. (1959). Studies in Molecular Dynamics. I. General Method. The Journal of Chemical Physics, 31(2), 459–466. https://doi.org/10.1063/1.1730376
[2]. Schlick, T. (2013). Molecular Modeling and Simulation. Springer Science & Business Media.
[3]. Refson, K. (2000). Moldy: a portable molecular dynamics simulation program for serial and parallel computers. Computer Physics Communications, 126(3), 310–329. https://doi.org/10.1016/s0010-4655(99)00496-8
[4]. Racine, J. (2006). gnuplot 4.0: a portable interactive plotting utility. Journal of Applied Econometrics, 21(1), 133–141. https://doi.org/10.1002/jae.885
[5]. Humphrey, W., Dalke, A., & Schulten, K. (1996). VMD: Visual molecular dynamics. Journal of Molecular Graphics, 14(1), 33–38. https://doi.org/10.1016/0263-7855(96)00018-5
[6]. Valtonen, M. J., & Hannu Karttunen. (2006). The three-body problem. Cambridge University Press.
[7]. Trenti, M., & Hut, P. (2008). N-body simulations (gravitational). Scholarpedia, 3(5), 3930. https://doi.org/10.4249/scholarpedia.3930
[8]. Goldberger, A. L. (1996). Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. The Lancet, 347(9011), 1312–1314. https://doi.org/10.1016/s0140-6736(96)90948-4
[9]. Rössler, O. E. (1976). Chaotic Behavior in Simple Reaction Systems. Zeitschrift Für Naturforschung A, 31(3-4), 259–264. https://doi.org/10.1515/zna-1976-3-408
[10]. P.C. Hohenberg, & Shraiman, B. I. (1989). Chaotic behavior of an extended system. Physica D Nonlinear Phenomena, 37(1-3), 109–115. https://doi.org/10.1016/0167-2789(89)90121-8
[11]. Barrow-Green, J. (1997). Poincaré and the three body problem. American Mathematical Society ; London.
[12]. van Gunsteren, W. F., & Berendsen, H. J. C. (1977). Algorithms for macromolecular dynamics and constraint dynamics. Molecular Physics, 34(5), 1311–1327. https://doi.org/10.1080/00268977700102571
[13]. Watson, C. (2023, September 23). We Just Got 12,000 New Solutions to The Infamous Three-Body Problem. ScienceAlert.
[14]. Breen, P. G., Foley, C. N., Boekholt, T., & Zwart, S. P. (2020). Newton versus the machine: solving the chaotic three-body problem using deep neural networks. Monthly Notices of the Royal Astronomical Society, 494(2), 2465–2470. https://doi.org/10.1093/mnras/staa713
[15]. Mendoza, M. L. Sanchez., Aguilar, M. A., & del Valle, F. J. Olivares. (1998). A mean field approach that combines quantum mechanics and molecular dynamics simulation: the water molecule in liquid water. Journal of Molecular Structure: THEOCHEM, 426(1-3), 181–190. https://doi.org/10.1016/s0166-1280(97)00319-9
[16]. Kaminski, G. A., Friesner, R. A., Tirado-Rives, J., & Jorgensen, W. L. (2001). Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. The Journal of Physical Chemistry B, 105(28), 6474–6487. https://doi.org/10.1021/jp003919d
[17]. Fujita, T., Nakano, T., & Tanaka, S. (2011). Fragment molecular orbital calculations under periodic boundary condition. Chemical Physics Letters, 506(1-3), 112–116. https://doi.org/10.1016/j.cplett.2011.02.055
Cite this article
Zhang,S. (2024). Physics Models and Machine Learning in Molecular Dynamics. Theoretical and Natural Science,55,34-40.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 2nd International Conference on Applied Physics and Mathematical Modeling
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Alder, B. J., & Wainwright, T. E. (1959). Studies in Molecular Dynamics. I. General Method. The Journal of Chemical Physics, 31(2), 459–466. https://doi.org/10.1063/1.1730376
[2]. Schlick, T. (2013). Molecular Modeling and Simulation. Springer Science & Business Media.
[3]. Refson, K. (2000). Moldy: a portable molecular dynamics simulation program for serial and parallel computers. Computer Physics Communications, 126(3), 310–329. https://doi.org/10.1016/s0010-4655(99)00496-8
[4]. Racine, J. (2006). gnuplot 4.0: a portable interactive plotting utility. Journal of Applied Econometrics, 21(1), 133–141. https://doi.org/10.1002/jae.885
[5]. Humphrey, W., Dalke, A., & Schulten, K. (1996). VMD: Visual molecular dynamics. Journal of Molecular Graphics, 14(1), 33–38. https://doi.org/10.1016/0263-7855(96)00018-5
[6]. Valtonen, M. J., & Hannu Karttunen. (2006). The three-body problem. Cambridge University Press.
[7]. Trenti, M., & Hut, P. (2008). N-body simulations (gravitational). Scholarpedia, 3(5), 3930. https://doi.org/10.4249/scholarpedia.3930
[8]. Goldberger, A. L. (1996). Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. The Lancet, 347(9011), 1312–1314. https://doi.org/10.1016/s0140-6736(96)90948-4
[9]. Rössler, O. E. (1976). Chaotic Behavior in Simple Reaction Systems. Zeitschrift Für Naturforschung A, 31(3-4), 259–264. https://doi.org/10.1515/zna-1976-3-408
[10]. P.C. Hohenberg, & Shraiman, B. I. (1989). Chaotic behavior of an extended system. Physica D Nonlinear Phenomena, 37(1-3), 109–115. https://doi.org/10.1016/0167-2789(89)90121-8
[11]. Barrow-Green, J. (1997). Poincaré and the three body problem. American Mathematical Society ; London.
[12]. van Gunsteren, W. F., & Berendsen, H. J. C. (1977). Algorithms for macromolecular dynamics and constraint dynamics. Molecular Physics, 34(5), 1311–1327. https://doi.org/10.1080/00268977700102571
[13]. Watson, C. (2023, September 23). We Just Got 12,000 New Solutions to The Infamous Three-Body Problem. ScienceAlert.
[14]. Breen, P. G., Foley, C. N., Boekholt, T., & Zwart, S. P. (2020). Newton versus the machine: solving the chaotic three-body problem using deep neural networks. Monthly Notices of the Royal Astronomical Society, 494(2), 2465–2470. https://doi.org/10.1093/mnras/staa713
[15]. Mendoza, M. L. Sanchez., Aguilar, M. A., & del Valle, F. J. Olivares. (1998). A mean field approach that combines quantum mechanics and molecular dynamics simulation: the water molecule in liquid water. Journal of Molecular Structure: THEOCHEM, 426(1-3), 181–190. https://doi.org/10.1016/s0166-1280(97)00319-9
[16]. Kaminski, G. A., Friesner, R. A., Tirado-Rives, J., & Jorgensen, W. L. (2001). Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. The Journal of Physical Chemistry B, 105(28), 6474–6487. https://doi.org/10.1021/jp003919d
[17]. Fujita, T., Nakano, T., & Tanaka, S. (2011). Fragment molecular orbital calculations under periodic boundary condition. Chemical Physics Letters, 506(1-3), 112–116. https://doi.org/10.1016/j.cplett.2011.02.055









