1. Theoretical preparation

1.1. Einstein's Special Theory of Relativity

In 1887, following Maxwell's suggestion[1], Michelson and Morley [2] conducted an experiment specifically designed to capture ether particles. Ultimately, they failed to find ether, and encountered a problem: the Galileo principle of velocity addition actually failed [3]. The Michelson-Morley experiment produced a result that the sum of the speed of light and the Earth's orbital speed was still the speed of light, which was obviously contrary to the Galileo principle of velocity addition.

To elucidate the phenomena observed in the Michelson-Morley experiment, FitzGerald proposed a hypothesis[4]: moving objects contract along their direction of motion, with the rate of contraction given by (1- \( \frac{{v^{2}}}{{c^{2}}} \) ). Building upon this foundation, Lorentz introduced an additional hypothesis[5][6][7]: moving objects undergo time dilation, quantified by 1/(1- \( \frac{{v^{2}}}{{c^{2}}} \) ). This led to the formulation of the Lorentz transformation. In 1905, Einstein revealed the fundamental insights from the Michelson-Morley experiment: light does not exhibit a velocity addition effect and maintains a constant speed for all observers, thereby establishing the principle of constancy of light's speed. Utilizing this principle, Einstein successfully derived the Lorentz transformation and formulated special relativity theory, which illuminated the relativity of space and time as well as their interrelation with matter's motion.

If it \( k \) is a -Galilean coordinate system, then every other coordinate system moving \( k \) with respect to a uniform translational motion \( {k^{ \prime }} \) is also a -Galilean coordinate system. \( {k^{ \prime }} \) With respect to, as with respect to, \( k \) the Galilean-Newtonian laws of mechanics hold. We shall take a step forward in our generalization if we state the above inference in the following terms: the \( {k^{ \prime }} \) actual evolution of natural phenomena with respect to a coordinate system in \( k \) constant motion without rotation will be governed by the \( {k^{ \prime }} \) same general laws as the actual evolution with respect to a coordinate system \( k \) , a statement called the principle of narrow relativity. The special theory of relativity presupposes that the speed of light is constant, that is to say, if there is a moving train, there are observers on the train and on the platform, and because of this premise, the speed of light measured by both is the same.

Einstein proposed[8] that the observer's state of motion would affect the observer's experience of space and time. The central idea of special relativity[9] can be expressed in a geometric form known as Minkowski spacetime. For Minkowski spacetime, when we introduce the imaginary number i into a four-dimensional Euclidean space, we can formally think of the Minkowski "world" as (with imaginary time coordinates), a four-dimensional Euclidean space. \( {x_{4}}=ict \) A thorough study of special relativity requires the introduction of the Lorentz transform, which has two important conclusions - time delay and length contraction, which explain the idea of why the observer's state of motion affects the observer's experience of space and time.

Special relativity also gave rise to one of the most famous equations in physics, Einstein's mass-energy relation

\( E=m{c^{2}}\ \ \ （1） \)

Not only did it theoretically prove the enormous amount of energy produced in a nuclear weapon explosion, it was also closely related to black hole physics.

1.2. General Relativity

General relativity adds the theory of gravity to special relativity, which is the theory we need to really understand black holes. In general relativity, space-time plays a major role in responding, or acting as, to the presence of massive objects

\( {G_{μν}}=\frac{8π{G_{N}}{T_{μν}}}{{c^{4}}}\ \ \ （2） \)

Governed by Einstein's equations, spacetime would become curved. When gravity is very weak, we can go back to Minkowski spacetime without curvature. That is, special relativity works. Gravity is very weak in most cases, so general relativity can be applied in many more cases.

To explain the curvature of spacetime, we must first introduce the concept of ordinary gravity. Ordinary gravity is what happens when all massive objects are moving relative to each other much slower than the speed of light and aren't dense enough to form a black hole. This is true in most places in the Milky Way, except near collapsing stars and the black hole at the center of the galaxy. Ordinary gravity is caused by gravitational redshift, which is why time slows down as you approach a massive object, and gravitational redshift is everywhere. The gravitational pull of a black hole is infinite, so space-time near the black hole is so curved that by the time the event horizon is reached, time in the usual sense comes to a complete stop.

The two pillars of general relativity are Einstein's equations and the principle of optimal proper time. In simple terms, matter tells space-time how to bend through Einstein's equations, and curved space-time tells matter how to move through the principle of optimal proper time.

2. Schwarzschild black holes

A Schwarzschild black hole describes the response of space-time to a mass point. This idea implies that matter tells spacetime how to bend, an idea that runs through Einstein's equations

\( {G_{μν}}=\frac{8π{G_{N}}{T_{μν}}}{{c^{4}}}\ \ \ （3） \)

The 10 functions of the metric tensor describe curved spacetime mathematically, and Einstein's equations show that the function must vary in just the right way throughout space and time to get a solution to the field equation, which was published by German astronomer Carl Schwasey in 1916.

2.1. Schwassy solution

Start by introducing the metric of the Hayward black hole

\( {ds^{2}}={-f(r)dt^{2}}+\frac{1}{f(r)}{dr^{2}}+{r^{2}}({dθ^{2}}+{sin^{2}}θ{dφ^{2}})\ \ \ （4） \)

Where: is the 00 component of the metric, M is the ADM mass of the black hole, and the variable is the four-dimensional coordinate variable. \( f(r)=1-\frac{{2Mr^{2}}}{{r^{3}}+{2l^{2}}M}t､r､θ､φ \)

When r goes to infinity, at this time, the black hole degenerates to the Schwarzschild metric: \( f(r)=1-\frac{2M}{r} \)

\( {ds^{2}}={-(1-\frac{2M}{r})dt^{2}}+\frac{1}{(1-\frac{2M}{r})}{dr^{2}}+{r^{2}}({dθ^{2}}+{sin^{2}}θ{dφ^{2}})\ \ \ （5） \)

If M=0, then overall spacetime degenerates to a flat Minkowski spacetime.

For a Schwarzschild black hole, its surface gravity is

\( κ({r_{+}})=\frac{1}{{2r_{g}}}\ \ \ (6) \)

Where, is the Schwarzschild radius, \( {r_{g}}=M \)

Similarly, the linear running potential V(r) is introduced, and the Lagrangian of this system is written using the metric formula (6)

\( L=\frac{1}{2}(-f(r)+\frac{{\dot{r}^{2}}}{f(r)}+{r^{2}}{\dot{φ}^{2}})+V(r)\ \ \ (7) \)

The effective potential is thus obtained

\( {V_{eff}}=-\frac{1}{2}(-{f_{1}}x+\frac{{L^{2}}}{x+{r_{+}}})-{V_{1}}x\ \ \ (8) \)

In order to study the instability maximum of the effective potential (8), different parameters are selected to study the behavior, as shown in Figure 1. Different lines in Figure 1 correspond to different L values. \( {V_{eff}} \) As can be seen from Figure 1, the value of the effective potential decreases with the increase of L, but the maximum value of instability also increases, indicating that the larger the angular momentum of the particle, the more distant the chaotic orbit is from the event horizon of the black hole. \( {V_{eff}}{x_{0}} \) However, when L=1, the effective potential does not have an instability maximum, which indicates that L must be large enough for the effective potential to have an instability maximum.

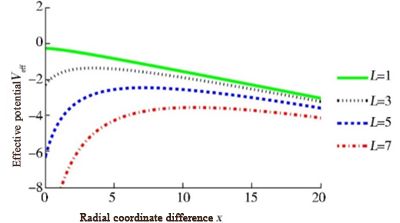
Figure 1. Image of the effective potential of a Schwarzschild black hole with different L corresponding to fixed parameters \( {V_{eff}}[10] \)

At the same time, the curve behavior of the Schwarzschild black hole under certain parameters is studied, taking the angular momentum L of the particle as the independent variable, combined with the Lyapunov exponential \( {λ^{2}}-{κ^{2}} \)

\( {λ^{2}}=-f(r)V_{eff}^{ \prime \prime }(r){|_{r={r_{0}}}}\ \ \ （9） \)

With the surface gravity of the Schwarzschild black hole equation (6), the curve under specific parameters can be obtained, as shown in Figure 2. \( {λ^{2}}={κ^{2}} \)

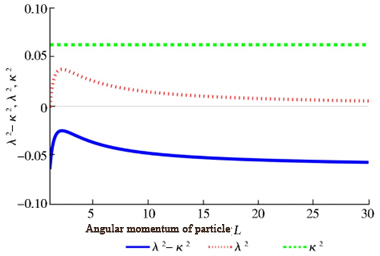
Figure 2. An image of a Schwarzschild black hole under certain parameters \( {λ^{2}}-{κ^{2}}[10] \)

It can be seen from Figure 2 that the curve increases first and then decreases, which also indicates that the chaos of the system increases with the increase of the angular momentum of the particles. However, if the angular momentum continues to increase, the influence of the black hole on the particles will become smaller and smaller, so the chaotic behavior will become smaller and smaller. \( {λ^{2}}-{κ^{2}} \)

2.2. Two characteristics of Schwarzschild black holes -- white holes and wormholes

The Schwarzschild metric has an opposite side to the black hole portion of spacetime, known as the "white hole." The white hole simply means that from the singularity, the flow of time drags all space away from the singularity, and everything passes through the one-way boundary to the outside. The proof that a white hole is part of the Schwarzschild solution is a paradox -- nothing can escape from a black hole, but a geodesic provides a possible escape route. The explanation for this paradox is that the geodesic comes not from the part of the Schwarzschild black hole, but from an entirely different part of spacetime -- the white hole, where spacetime flows in the exact opposite direction of the black hole, and its interior points to a place where the radial coordinates are less than the Schwarzschild radius. White holes appear in the past, or arbitrarily distant past, while black holes appear in the future, where they are part of the future.

Based on the expansion of our view of space-time on the noncausal path, another feature of the Schwarzschild solution, the wormhole or Einstein-Rosenbridge, is discovered, which connects one external world to another external world with the same geometry, and the only connection between the two is the noncausal path inside the black hole or white hole that neither massless nor massless particles can follow. In simple terms, the two are causally disconnected from each other, but overlap internally, and wormholes are thought to be a bridge between two extremely distant points in the universe.

3. Black holes spin on their axis

While the Schwarzschild solution, as articulated by the Einstein field equations, accurately characterizes a solitary, static, non-rotating black hole, such entities do not exist in our actual universe. Consequently, an extension of the Schwarzschild solution was necessitated to explore rotating black holes. In tribute to its discoverer, the eminent mathematician Roy Kerr, this extension is referred to as the Kerr black hole. Black holes in the cosmos are predominantly rotating or spinning; as they do so, they exert a drag on their surrounding spacetime—a phenomenon known as 'frame dragging'—which induces a novel precession in geodesics. For a Schwarzschild black hole, precession pertains solely to two-dimensional orbital rotation. Conversely, for a Kerr black hole, it encompasses the twisting of the orbit itself due to frame dragging—analogous to the rotation of the black hole about its own axis. As particles approach closer to the black hole's event horizon, frame dragging accelerates significantly; within regions of high energy levels, this effect becomes extreme and compels all nearby particles to rotate around the black hole.

An electrically charged black hole represents a solution to both Maxwell's equations of electromagnetism and Einstein's field equations. Nevertheless, it is generally accepted that black holes in the universe are electrically neutral, rendering the study of charged black holes seemingly less critical. However, certain phenomena associated with charged black holes remain significant for our understanding of these cosmic entities. For instance, when a black hole possesses sufficient charge, its event horizon ceases to exist; this observation clearly contradicts established reality, indicating that there must be an upper limit on the charge a black hole can possess. Similarly, while the angular momentum of a Kerr black hole cannot be infinite—despite the fact that charge or spin does not fundamentally alter spacetime outside the event horizon—it profoundly influences conditions within.

All celestial bodies in the universe possess angular momentum, albeit in varying magnitudes, resulting from the intricate dynamic interactions with surrounding matter during their formation and evolution. This phenomenon also implies that black holes within our universe exhibit certain common characteristics, leading to the conclusion that zero-angular-momentum Schwarzschild black holes cannot exist. The rotation of a black hole induces a distortion in the adjacent spacetime, causing its geometry to deviate from spherical symmetry. To address this issue, Kerr proposed an axially symmetric solution characterized by fewer constraints; it possesses a single axis of symmetry and maintains its geometric properties when rotated around this axis. Consequently, this simplification renders the field equations governing rotating black holes more tractable. Conversely, it indicates that field equations for black holes lacking an axis of symmetry become exceedingly complex. Nevertheless, the no-hair theorem asserts that any given black hole will rapidly shed any transient features it may possess and settle into a unique stable state. In essence, a black hole cannot sustain long-term asymmetric attributes; thus, solutions representing stable state black holes derived from the more intricate Einstein field equations are untenable.

Although the Schwarzschild solution characterizes a non-rotating black hole, which does not exist in reality, the investigation of Schwarzschild black holes remains significantly important because many characteristics of black holes are not qualitatively influenced by spin. For instance, the time dilation experienced by different observers approaches infinity as they near the event horizon; this horizon acts as a one-way boundary, and once an object crosses it, spacetime collapses inward. While these effects may vary in detail and can differ substantially, their fundamental nature remains unchanged.

Two significant ways in which the rotation of a black hole alters the geometry of spacetime are as follows: first, as one approaches the event horizon, the flat or bulging phenomenon becomes increasingly pronounced; moreover, this effect intensifies with greater rotational velocity of the black hole. Second, it induces a flow of spacetime around the black hole, with this flow accelerating as one nears the event horizon. In terms of spacetime dynamics, this phenomenon is referred to as frame dragging—an effect not exclusive to black holes. The Earth also produces this effect due to its rotation; however, when compared to that generated by black holes, it is exceedingly minor and thus often overlooked.

Black holes cannot rotate at arbitrary speeds; however, in mathematical terms, the spin of the Kerr solution can exceed the theoretical maximum, resulting in the disappearance of their event horizon—thus ceasing to be classified as black holes. In the absence of an event horizon, singularities within spacetime would become exposed to the external universe, and general relativity is unable to predict their future behavior. The implications of this exposure remain unclear, even within simulated universes where such scenarios have not been successfully realized. British physicist and mathematician Sir Roger Penrose proposed the cosmic censorship conjecture decades ago, asserting that all natural singularities in the universe will be 'covered' by event horizons. From a physicist's standpoint, if nature adheres to this principle, it would profoundly influence our understanding of physical reality. This is predicated on our belief that general relativity's predictions regarding spacetime singularities represent its limitations; should nature indeed operate under these rules, it would affirm their validity without necessitating conjectures based solely on general relativity.

In comparison to the Schwarzschild black hole, the Kerr black hole exhibits a more intricate geometry due to its rotation, introducing frame-dragging effects that influence the trajectories of particles approaching the event horizon. Let us consider a simplified scenario: if we were to deploy detectors equipped with flashlights from various directions into a Schwarzschild black hole, an external observer would never witness these detectors crossing the event horizon; instead, as they near this boundary, they appear to decelerate and enter a stable state characterized by an increasing redshift in the frequency of their emitted light [3]. A similar phenomenon is anticipated for a Kerr black hole, where this behavior will perpetually rotate in accordance with the rotational period of the black hole.

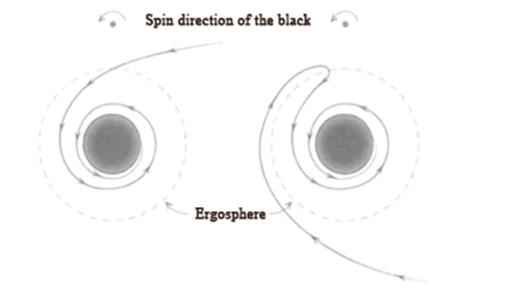
Figure 3. Effect of reference frame drag on geodesics falling into a Kerr black hole (rotating black hole)[11]

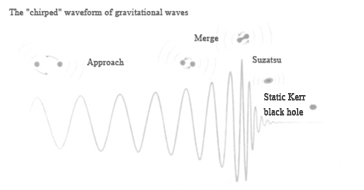
Figure 4. The "chirped" gravitational wave waveform produced by the collision of the two black holes[11]

4. Collision of black holes

The black holes previously discussed were all mutually isolated systems. However, it is evident that in nature, there are no completely isolated black holes; they always exert certain influences on one another. Einstein's field equations provide the mathematical form of how matter curves spacetime. When there is no matter, spacetime becomes non-curved, that is, it turns into a completely flat spacetime. Apparently, a completely flat spacetime is not the sole solution of the vacuum Einstein field equations. The spacetime of isolated black holes also complies with it, and the mutually orbiting black holes also offer a solution to the vacuum field equations. Moreover, a pair of mutually orbiting black holes will merge into a rapidly spinning Kerr black hole.

Collisions of black holes are the most violent events in the field of general relativity. When we think of colliding black holes, we naturally picture two approaching black holes hurtling towards each other and finally colliding. But black holes aren't widespread in the universe, and they're so far apart from each other that black hole collisions are highly unusual in random collisions.

More common are binary systems of stars, stars with enough mass that they collapse into black holes at the end of their lives, forming binary black hole systems that don't collide immediately but eventually do because they don't have enough velocity to escape each other's gravitational pull. Gravitational waves are generated throughout the evolution of the binary black hole, after a long, gradual phase of rotation, the event horizons of the two black holes merge, and then through the bell phase, finally forming a stable Kerr black hole.

In summary, gravitational waves are generated during the evolution of a binary black hole system, which experiences an extended and gradual inspiral phase prior to the merger of the two black holes. This is followed by a chirp phase that culminates in the formation of a stable Kerr black hole. However, the duration for gravitational wave production is exceedingly brief, posing significant challenges for detection. The chirp signal within LIGO's sensitivity range lasts less than one second; larger black holes produce lower-frequency chirps, while smaller black holes emit longer-duration chirp signals that conclude with a pronounced shout. The frequency of these chirp signals is intrinsically linked to the total mass of the merging black holes since gravitational wave chirps arise from multiple pre-merger orbits. The duration of these orbits correlates directly with the final event horizon radius, which itself is proportional to the total mass of the black hole.

The amplitude of a wave is directly proportional to the transmission distance; thus, the amplitude of the chirp signal emitted by gravitational waves in proximity to a black hole is greater than that from a more distant black hole. Consequently, by beginning with the resolution of Einstein's vacuum field equations to elucidate the strength and frequency characteristics of chirp signals produced during any binary black hole merger, we can deduce both the distance of the binary black hole system from Earth and its total mass through an analysis of these signal attributes.

The majority of black hole collisions are classified as 'spin-in' mergers, which can be effectively described through the numerical resolution of Einstein's equations. By simulating a range of initial conditions numerically, we can derive insights into the gravitational radiation emitted during black hole mergers, thereby enhancing our understanding of these cosmic events.

5. Black hole thermodynamics

Entropy is a concept in thermodynamics and also represents the degree of disorder. It is not difficult for people to understand the concept of entropy, as many things in life can help us understand it, such as the headphone wires in our pockets always getting tangled, and "wine is fragrant even in a narrow alley." These all convey the message that the entropy of an isolated system always spontaneously increases, or that the system always has a tendency to approach disorder spontaneously. This is what the second law of thermodynamics describes: the entropy of an isolated system can only increase and not decrease. Bekenstein [12] conducted a series of thought experiments to show that black holes should also have entropy, and the entropy carried by a black hole is proportional to the area of its event horizon. Later, Hawking [13] used quantum field theory techniques in curved spacetime to rigorously prove that black holes have thermal radiation, thus having thermodynamic properties such as temperature and entropy. This all proves that black holes are a thermodynamic system.

The expression for black hole entropy contains several fundamental constants of nature: the gravitational constant, the speed of light, Planck's constant, and Boltzmann's constant, all of which show that black hole thermodynamics is essentially an effect of quantum gravity[14].

5.1. The zeroth law of black hole thermodynamics

Traditional black holes are believed to possess a surface escape velocity that exceeds the speed of light, while Einstein's general theory of relativity delineates the motion of objects within a gravitational field, establishing the speed of light as an ultimate limit beyond which no object can travel. Consequently, in such stellar entities, no form of matter can be emitted, including photons. The event horizon surrounding a black hole is characterized as the demarcation between observable and unobservable events in spacetime[15]. Hawking investigated the quantum phenomena associated with black holes and posited that classical physics prohibits any matter from escaping the event horizon; however, when considering quantum tunneling effects, there exists a finite probability for matter entering a black hole to escape—this phenomenon is termed Hawking radiation. In 1975, Hawking employed quantum field theory in curved spacetime to derive the spectrum of Hawking radiation and discovered its remarkable similarity to that of blackbody radiation. A comparison between these two spectra revealed that black holes exhibit temperature.

\( T=\frac{κ}{2π}\ \ \ （10） \)

That is, the definition of temperature in black hole thermodynamics, that is, the zero law of black hole thermodynamics.

5.2. The first law of black hole thermodynamics

Similar to the traditional first law of thermodynamics, a thermodynamic system is satisfied when it goes through a quasi-static process and reaches a new static state

\( δE=TδS-PδV\ \ \ （11） \)

For a steady-state axisymmetric black hole that undergoes an infinitesimal physical process to become a steady-state axisymmetric black hole again, yes

\( δM=\frac{1}{8π}κδA+ΩδJ+ϕδQ\ \ \ （12） \)

This is the first law of thermodynamics for black holes.

5.3. Second Law of thermodynamics for black holes

Bekenstein states that black holes have entropy and defines it

\( S=\frac{A}{4}\ \ \ (13) \)

Where A is the area of the event surface, Hawking proved the area law of black holes under the condition of cosmic supervision principle and energy grab: that is, the surface area of black holes never decreases

\( δA≥0\ \ \ （14） \)

This is known as the second law of thermodynamics for black holes.

5.4. Third Law of Thermodynamics for black holes

In black hole physics, for a general Kerr black hole, the surface gravity of its event horizon takes

\( κ=\frac{({M^{2}}-{a^{2}}-{Q^{2}}{)^{\frac{1}{2}}}}{2M[M+({M^{2}}-{a^{2}}-{Q^{2}}{)^{\frac{1}{2}}}]-{Q^{2}}}\ \ \ （15） \)

The temperature of a black hole is zero, which means the surface gravity is satisfied \( κ=0 \)

\( {M^{2}}={a^{2}}+{Q^{2}}\ \ \ (16) \)

So it turns out that[16] the closer a black hole gets to an extreme black hole, the harder it is to make its surface gravity drop. So we can make it

"It is impossible to reduce the surface gravity of a black hole to zero by finite physical processes."

Called the third law of thermodynamics for black holes.

5.5. Recent Research on Black Hole Thermodynamics

One of the most significant studies in the realm of black hole thermodynamics in recent years is the extension of thermodynamics, often referred to as black hole thermodynamics within an extended phase space. The Smarr relation establishes connections among physical quantities such as black hole mass, temperature, entropy, and cosmological constant. However, the cosmological constant diverges from other physical quantities and does not appear directly in the conventional first law of black hole thermodynamics. Consequently, it becomes imperative to introduce the cosmological constant as an additional variable to bridge the Smarr relation with the first law of black hole thermodynamics. In addressing this issue, the Smarr relation offers pertinent insights for extending the first law of black hole thermodynamics and leads to a formulation of black hole thermodynamics within an extended phase space[17].

The extended black hole thermodynamics has rich physical theoretical application prospects. The extended thermodynamic form provides a basis for studying phase transitions in black holes and has generated a research direction called black hole chemistry [18]. The extended black hole thermodynamics contains many novel thermodynamic behaviors beyond ordinary matter systems [19]. Finally, the extended black hole thermodynamics has also been applied in research areas such as holographic complexity [20], weak cosmological censorship conjecture [21], and weak gravitational conjecture [22].

6. Conclusion

The exploration of black holes commenced in the 19th century, evolving from theoretical foundations rooted in Einstein's theory of relativity to the groundbreaking direct observation of black holes by the Event Horizon Telescope (EHT) on April 10, 2019. The investigation of black holes has constituted a pivotal focus within astrophysics for over a century. From Schwarzschild black holes to Kerr black holes, and from isolated static configurations to dynamic systems involving orbiting and colliding black holes, as well as advancements in black hole thermodynamics and extended phase space formulations, humanity's inquiry into these enigmatic entities has been relentless.

Black holes are mysterious objects in astronomical research. Their unique properties have led many teams to devote themselves to them. Some even believe that the study of black holes will be an effective way to achieve interstellar travel and time travel. The study of black holes has only discovered the tip of the iceberg, and the mystery of black holes remains to be explored.