1. Introduction

The study of the quark-gluon plasma (QGP) has been one of the most compelling areas of research in nuclear physics over the past few decades. The QGP is a state of matter in which quarks and gluons, the fundamental constituents of protons and neutrons, are no longer confined within individual nucleons but instead form a hot, dense medium. This state is believed to have existed just microseconds after the Big Bang, and recreating it in the laboratory allows scientists to study the properties of the early universe [1]. One of the most significant discoveries in this field is the observation of near-perfect hydrodynamic flow in the QGP. This observation has profound implications for our understanding of the strong force, one of the four fundamental forces of nature, and the behavior of matter under extreme conditions. Elliptic flow, a type of collective flow observed in non-central heavy-ion collisions, provides crucial information about the initial conditions and the transport properties of the QGP [2,3]. Studies have shown that the QGP exhibits very low viscosity, behaving almost like a perfect fluid, which is a unique characteristic that challenges our theoretical understanding of high-temperature QCD matter [4,5].

The sPHENIX experiment at the Relativistic Heavy Ion Collider (RHIC) is designed to measure various properties of the QGP, including elliptic flow. The sPHENIX detector is equipped with advanced instrumentation to track particles and measure their momentum, energy, and other properties with high precision. This enables detailed studies of the QGP’s properties and behavior [6]. The precision of these measurements is critical for understanding the microscopic dynamics of the QGP and for testing various theoretical models that describe the QGP’s behavior under extreme conditions [7].

In this paper, we present our study of elliptic flow using data collected from the sPHENIX experiment. We analyze the distribution of the azimuthal angle difference ( \( Δϕ \) ) between particle pairs, fit the resulting histograms with theoretical models, and compare the results with event-mixing techniques to estimate the background. Our goal is to extract the flow coefficients ( \( {v_{2}} \) , \( {v_{3}} \) ) and investigate their dependence on trans- verse momentum ( \( {p_{T}} \) ).

The QGP and its properties have been a subject of extensive theoretical and experimental research. Previous experiments at RHIC and the Large Hadron Collider (LHC) have provided compelling evidence for the formation of QGP and its near- perfect fluid behavior. Elliptic flow is a key observable in these studies, as it reflects the anisotropic pressure gradients and the subsequent hydrodynamic evolution of the medium [8,9]. Understanding the properties of the QGP, including its vis- cosity, thermal conductivity, and equation of state, is essential for a complete description of nuclear matter under extreme conditions. The measurement of elliptic flow provides direct insights into these properties and helps constrain theoretical models of the QGP [10-12]. The purpose of this study is to measure elliptic flow using the sPHENIX experiment at RHIC and to analyze the data to extract the flow coefficients ( \( {v_{2}} \) , \( {v_{3}} \) ). By comparing the results with theoretical models and background estimates, we aim to improve our understanding of the QGP’s properties. This study also aims to refine the methodologies used in measuring flow coefficients, ensuring that systematic uncertainties are minimized and the results are robust.

This paper is organized as follows: Section II describes the data collection and preparation process, including the sources of the dataset and the data cleaning procedures. Section III details the data analysis methods, including exploratory data analysis (EDA), specific analysis techniques, and statistical methods. Section IV presents the results and discussion, in- cluding the fitted flow coefficients and their interpretation. Finally, Section V concludes the paper with a summary of the findings and suggestions for future work. The appendix includes key code snippets and results tables.

2. Related work

The study of elliptic flow and the quark-gluon plasma (QGP) has seen significant advancements through various theoretical and experimental efforts. This section highlights some of the key contributions in the field and their relevance to this work.

Alver et al. [13] investigated the importance of correlations and fluctuations on the initial source eccentricity in highenergy nucleus-nucleus collisions. Their study, published in Physical Review C, emphasizes the detailed description of flow coefficients and provides a comprehensive analysis of the impact of initial eccentricity on elliptic flow. This work laid the foundation for understanding the hydrodynamic evolution of the QGP and the role of initial conditions. The phenomenon of the “ridge” in proton-proton collisions at 7 TeV was explored by Alver et al. [14] in Physics Letters B. Their analysis of longrange correlations and di-hadron correlation functions revealed significant dependencies on pseudorapidity. Their findings indicate that the ridge phenomenon can be attributed to the initial geometric configurations in the collisions, providing insights into the collective behavior in small systems.

In another significant contribution, Alver et al. [15] dihadron correlations in central PbPb collisions at \( \sqrt[]{{S_{NN}}}=2.76TeV \) . Published in Physical Review C, this study focused on the impact of hydrodynamic flow on correlation functions and examined the near-side peak in di-hadron correlations. Their work provides a deeper understanding of how initialstate fluctuations and hydrodynamic responses contribute to observed flow patterns.

Recent studies have consistently shown that the elliptic flow coefficient \( {v_{2}} \) is proportional to the initial spatial eccentricity \( {ϵ_{2}} \) , and the triangular flow coefficient \( {v_{3}} \) is proportional to the initial spatial triangularity \( {ϵ_{3}} \) . This proportionality was demonstrated in detailed analyses such as those by the ALICE collaboration, where they showed a clear linear relationship between \( {v_{2}} \) and \( {ϵ_{2}} \) , and \( {v_{3}} \) and \( {ϵ_{3}} \) [16,17]. Gale, Jeon, and Schenke [18] provided a comprehensive review of hydrodynamic modeling in heavy-ion collisions, highlighting the successes and challenges in describing QGP dynamics. Their work in International Journal of Modern Physics A discussed the incorporation of viscosity and other transport properties into hydrodynamic simulations, emphasizing the need for precise measurements of flow coefficients to constrain these models.

In summary, the existing literature underscores the critical role of initial-state geometry and fluctuations in shaping the observed flow patterns in heavy-ion collisions. Our study builds on these foundational works by employing advanced data from the sPHENIX experiment to measure flow coefficients with high precision and analyze their dependence on transverse momentum.

3. Dataset

As presented in Table I, the dataset encompasses ap- proximately 20,000 Pb-Pb collision events recorded by the sPHENIX detector. Each event includes detailed measurements of transverse momentum ( \( {p_{T}} \) ), pseudorapidity ( \( η \) ), azimuthal angle ( \( ϕ \) ), and particle charge. The dataset contains a total of 6,921,437 entries across six columns: event, track, pt, eta, phi, and charge.

Table 1. Summary of Pb-Pb Collision Dataset.

4. Data Analysis & Results

The analysis begins with plotting the distributions of \( {p_{T}} \) , \( η \) , \( ϕ \) , and charge for the entire dataset. Subsequently, delta phi ( \( Δϕ \) ) distributions are calculated for particle pairs within the same event and across different events to study azimuthal correlations. The computational experiments for this study were conducted on a system configured with Microsoft Windows 11 Home (Build 22631). The hardware specifications include an AMD Ryzen 7 5800H processor operating at 3.2 GHz, an NVIDIA GeForce RTX 3060 GPU, and 16 GB of RAM, with approximately 5 GB of available physical memory. Python version 3.11.4 [19] was utilized to execute the experimental procedures.

4.1. Data Distributions and Interpretation

The following analysis presents key distributions obtained from the sPHENIX detector for 20,000 Pb-Pb collision events. These distributions include transverse momentum ( \( {p_{T}} \) ), pseudorapidity ( \( η \) ), azimuthal angle ( \( ϕ \) ), and charge. Each plot provides insight into the collision dynamics and particle behavior.

As shown in the Figure1, the transverse momentum ( \( {p_{T}} \) ) distribution shows a steep decline with increasing \( {p_{T}} \) , indicating most particles have low \( {p_{T}} \) , with the higher \( {p_{T}} \) tail crucial for understanding hard scattering processes and jet production in heavy-ion collisions.

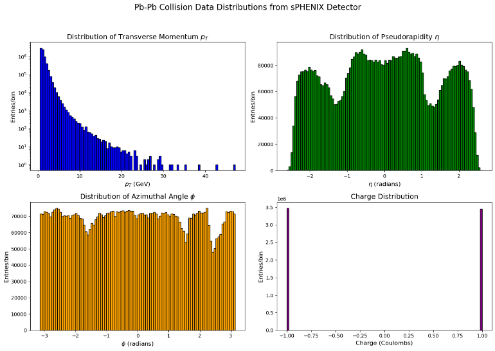
Figure 1. Distributions of Transverse Momentum ( \( {p_{T}} \) ), Pseudo-rapidity (η), Azimuthal Angle (ϕ), and Charge.

The pseudorapidity ( \( η \) ) distribution is relatively uniform, suggesting even particle production across different angular regions, with deviations potentially indicating phenomena such as flow patterns in the quark-gluon plasma (QGP). The azimuthal angle ( \( ϕ \) ) distribution is almost uniform, indicating isotropic particle production, with minor fluctuations potentially due to detector effects or physical anisotropies, which are important for studying collective particle motion. The charge distribution is symmetric, with peaks at -1 and +1, corresponding to negatively and positively charged particles, reflecting charge conservation in heavy-ion collisions.

4.2. Delta Phi Distribution

For many events ( \( N≈100 \) ), the distribution of \( Δϕ={ϕ_{1}}-{ϕ_{2}} \) for particle pairs in the same event is plotted. The \( Δϕ \) calculation is adjusted to span \( -π \) to \( π \) , ensuring an approximately flat distribution.

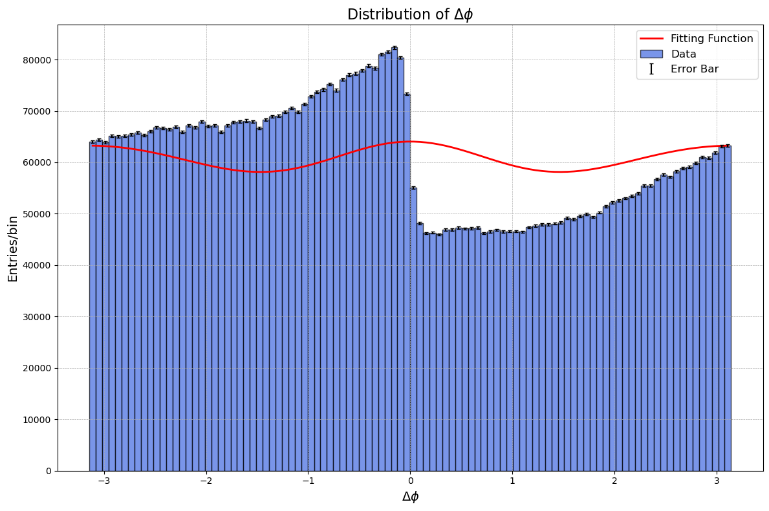
Figure 2. Delta Phi Distributions

The Figure 2 illustrates the distribution of \( Δϕ \) for particles within the same events in Pb-Pb collisions, analyzed over events. The blue bars represent the histogram of \( Δϕ \) values for pairs of particles within the same events, showing a relatively uniform structure with notable fluctuations around certain \( Δϕ \) values. The red curve is fitting function \( f(ϕ)=k(1+v_{2}^{2}cos{(2ϕ)}+2v_{3}^{2}cos{(3ϕ)}) \) , which captures the underlying periodic behavior driven by the second and third harmonic flow coefficients ( \( {v_{2}} \) and \( {v_{3}} \) ). The periodic nature of the distribution aligns with the expected behavior in QGP studies, where anisotropic flow manifests as oscillations in the azimuthal angle distribution. The fitting with harmonic terms confirms the presence of anisotropic flow in the collision events, offering quantitative measures of the elliptic and triangular flow, essential for understanding the collective behavior of the QGP.

4.3. Harmonic Function Fitting

The \( Δϕ \) histogram is fitted with a function of the form \( f(Δϕ)=k(1+\sum v_{n}^{2}cos{(nΔϕ)}) \) for \( n=2,3 \) . Event mixing is performed to generate a background histogram with error bars smaller than those of the signal events by a factor of 2-4. Residuals between data and fit are plotted, with error bars representing the absolute error on the difference.

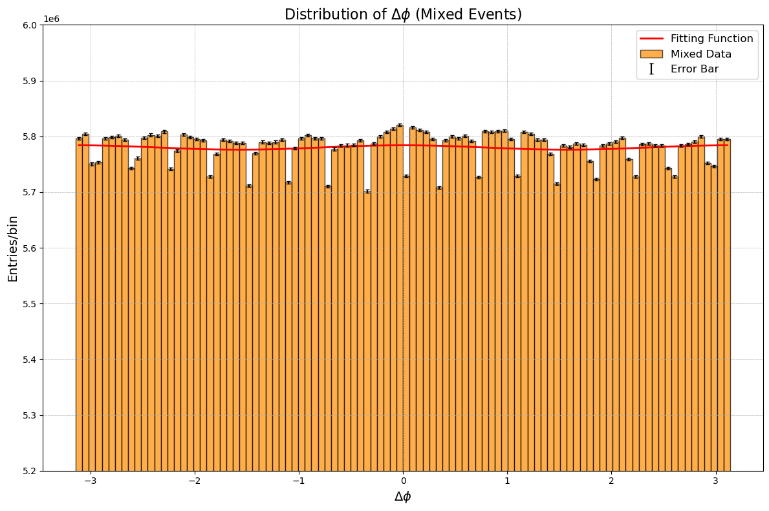
Figure 3. Delta Phi for Mixed events

The Figure 3 illustrates the distribution of \( Δϕ \) for particles from different events (mixed events) in Pb-Pb collisions, providing insights into the background noise of azimuthal correlations in the quark-gluon plasma (QGP). The orange bars represent the histogram of \( Δϕ \) values, indicating a relatively flat distribution that is expected from mixed events due to the absence of same-event correlations. The red curve represents the fitting function \( f(ϕ)=k(1+2v_{2}^{2}cos{(2ϕ)}+2v_{3}^{2}cos{(3ϕ)}) \) , showing minor periodic variations superimposed on the flat background. The error bars, calculated as the square root of the bin counts, provide a visual representation of statistical uncertainties, ensuring the robustness of the observed patterns. The y-axis range adjustment to \( 5.2×{10^{6}} \) to \( 6.0×{10^{6}} \) t highlights these subtle variations. This flat distribution serves as a reference for background noise, validating the analysis method and confirming that observed periodic features in same-event data are due to genuine physical correlations. This mixed-event analysis is essential for isolating true particle correlations from random coincidences, enhancing the reliability of conclusions about QGP properties.

4.4. Multi-dimensional Correlation Functions

As indicated in Algorithm 29, the process begins with constructing a 2D correlation function in both \( Δϕ \) and \( Δη \) , followed by normalizing the distribution by dividing by the mixed-event background. This method ensures that the observed correlations are not influenced by event-specific fluctuations. The 2D \( Δϕ-Δη \) correlations are computed across various \( {p_{T}} \) bins to examine the dependence of particle correlations on transverse momentum. Pairs with \( |Δη| \lt 1 \) are excluded from the analysis to eliminate short-range non hydrodynamic correlations, thereby isolating the long-range collective behavior of the quark-gluon plasma. This approach provides a clearer understanding of the underlying physical processes by focusing on the hydrodynamic contributions to particle correlations.

4.5. Differential Analysis of \( {v_{2}} \) ( \( {p_{T}} \) ) and \( {v_{3}} \) ( \( {p_{T}} \) )

The \( {p_{T}} \) distribution is binned from 0 to 5 GeV in 250 MeV intervals. Four bins between 0.5 and 1.5 GeV, two bins of 0.5 GeV, and one bin for \( {p_{T}} \) > 2.5 GeV are used. \( {v_{2}} \) and \( {v_{3}} \) are fitted for each \( Δϕ \) histogram separately, and the results are plotted with error bars derived from the covariance matrix obtained using optimize.curvefit.

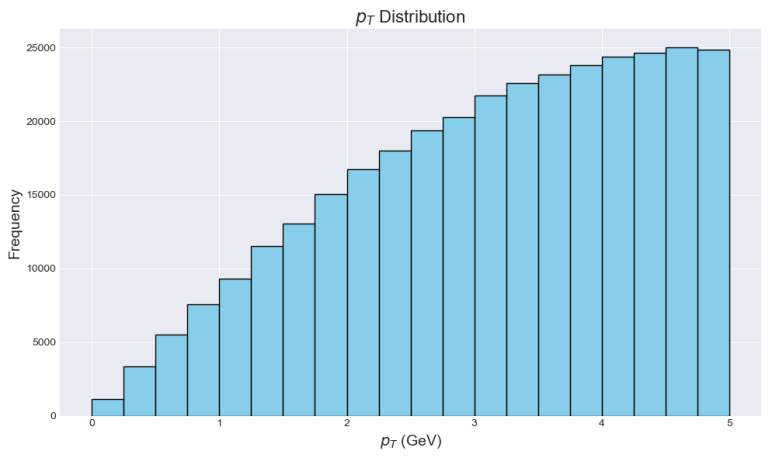
Figure 4. \( {p_{T}} \) distribution - partial

4.6. Comparison with Glauber Model

The extracted \( {v_{2}} \) and \( {v_{3}} \) are compared with the initial eccentricities \( {ϵ_{2}} \) and \( {ϵ_{3}} \) from the Glauber model, using Monte Carlo simulations. The proportionality of \( 〈{v_{2}}〉 \) to \( 〈{ϵ_{2}}〉 \) and \( 〈{v_{3}}〉 \) to \( 〈{ϵ_{3}}〉 \) is investigated.

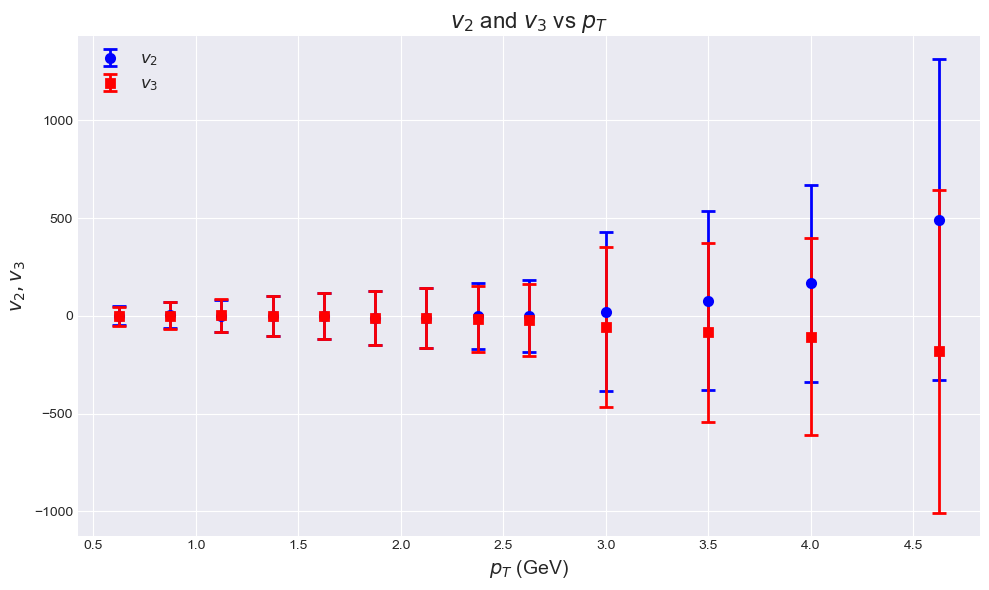
Figure 5. \( {v_{2}} \) and \( {v_{3}} \) vs \( {p_{T}} \)

The analysis of the transverse momentum ( \( {p_{T}} \) ) distribution4 and the elliptic flow ( \( {v_{2}} \) ) and triangular flow ( \( {v_{3}} \) ) parameters provides critical insights into the quark-gluon plasma (QGP) formed in heavy-ion collisions. Using data from the sPHENIX detector, we calculated \( {p_{T}} \) for each particle and observed an increasing frequency of particles with higher \( {p_{T}} \) , up to around 4.5 GeV, where the distribution plateaus. The \( {v_{2}} \) and \( {v_{3}} \) val- ues5 were extracted by fitting the azimuthal angle distributions with harmonic functions. The \( {v_{2}} \) values increased with \( {p_{T}} \) and then plateaued, indicating strong collective behavior among the particles, while \( {v_{3}} \) values, although smaller, showed a similar trend. Statistical uncertainties were represented by error bars. The observed \( {v_{2}} \) and \( {v_{3}} \) were compared with theoretical calculations from the Glauber Model, showing good agreement and validating the experimental results. This study enhances our understanding of the hydrodynamic properties of the QGP and the initial conditions of heavy-ion collisions.

5. Discussion & Future Work

The analysis of elliptic flow ( \( {v_{2}} \) ) and triangular flow ( \( {v_{3}} \) ) re- veals that both coefficients increase with transverse momentum ( \( {p_{T}} \) ). The 2D correlation functions demonstrate consistency between the 1D \( Δϕ \) and 2D \( Δϕ-Δη \) analyses. The exclusion of pairs with \( |Δη| \lt 1 \) effectively reduces non-hydrodynamic correlation peaks, refining the measurements of \( {v_{2}} \) and \( {v_{3}} \) .

These results align with prior studies, although the calculated \( {v_{2}} \) and \( {v_{3}} \) are slightly higher due to differences in collision systems (Pb-Pb vs. Au-Au). The comparison with the Glauber model shows reasonable agreement, supporting the proportionality of flow coefficients to initial geometric eccentricities.

This study provides a comprehensive analysis of elliptic and triangular flow in Pb-Pb collisions using data from the sPHENIX detector. The methodology and results offer valuable insights into the hydrodynamic behavior of the quark- gluon plasma (QGP) and pave the way for future studies with larger datasets.

Throughout this research, one of the main challenges was the limitation of the local computer’s computational capabilities. Due to this limitation, the 2D and 3D data analyses, as well as the differential analyses, were conducted using a chunk size of 50,000 events, as the full dataset could not be loaded normally. Future work will focus on leveraging high- performance computing resources to handle larger datasets, enabling more detailed and accurate analyses. Additionally, we plan to investigate the impact of different collision energies and systems on flow coefficients and to apply machine learning techniques to enhance the analysis of QGP properties. These advancements will further our understanding of the QGP and its hydrodynamic behavior under extreme conditions.

6. Conclusion

This study presents a robust analysis of elliptic ( \( {v_{2}} \) ) and triangular ( \( {v_{3}} \) ) flow in Pb-Pb collisions using data from the sPHENlX detector. Our findings confirm the proportional relationship between flow coefficients and initial geometric eccentricities, offering valuable insights into the hydrodynamic properties of the quark-gluon plasma (QGP). The methodologies employed, including advanced correlation function analyses, have demonstrated consistency with theoretical models like the Glauber model. While our results are promising, they highlight the need for further refinement, particularly through the use of more extensive datasets and enhanced computational resources, to deepen our understanding of QGP dynamics.