1. Introduction

Heat dissipation is a crucial part of machine design, especially for systems that continuously generate heat during operation. Effective heat dissipation measures are essential to prevent component from overheating and damage, and even system crashes. Usually, to conduct heat out of a designated area, materials with high thermal conductivity such as metals are used. However, in addition to the thermal conductivity of the material, adjusting the geometric shape and internal structure of the cooling system can also significantly improve the heat dissipation efficiency. One of the common approaches is introducing porous media.

Previous studies have delved into various aspects of heat conduction in porous media, particularly the relationship between pore shape and effective thermal conductivity. For example, Smith et al. found that pore shapes are relevant to overall thermal conductivity. Thus, through adjusting them, heat transfer performance can be optimized based on specific applications [1]. However, research on the impact of aperture, a key parameter involved, is still insufficient.

The pore size directly affects the balance between two distinct types of heat transfer which are solid-phase conduction and gas-phase conduction. Larger pores usually induce more gas-phase conduction, thus improving overall thermal conductivity in many cases. This phenomenon is especially important in applications involving radiators and heat exchangers. The Maxwell Eucken model provides a mathematical framework to help us understand how pore size and its distribution affect the effective thermal conductivity of mixtures that consists of multiple materials [2].

In recent years, research has further expanded our understanding of the factors affecting the thermal conductivity of porous media. For instance, through the method of numerical analysis, the effect of pore size distribution on overall thermal conductivity was investigated by Zhang, Huang and Liu. The results showed that under certain conditions, the increase of pore size would directly improve the thermal performance [3]. Similarly, Nguyen, Vo, and Pham pointed out that the connectivity of pores plays an important role in thermal conduction as well [4]. The porosity (i.e. pore volume fraction) of a material largely determines its thermal conductivity. Yang and Yu concluded that as the porosity increases, the effective thermal conductivity usually decreases because more air fills the pores, thus disrupting the solid's thermal conductivity path [5]. However, at a fixed porosity, the balance between solid-phase and gas-phase conduction can be optimized. Chen, Li, and Zhou found that adjusting pore size can adapt thermal conductivity to specific requirements [6].

In addition, the arrangement direction of pores in the material is also a factor affecting thermal conductivity. The study by Li, Sun, and Wang showed that arranging pores along the direction of heat flow can significantly improve thermal conductivity compared to randomly arranging them [7]. Finally, the type of material used is also crucial in porous media. Bianchi, Manzolini, and Silva discovered that even materials with extremely high intrinsic thermal conductivity will experience a significant decrease in overall thermal conductivity after the introduction of pores that interrupts the thermal conduction path [8]. Based on the research mentioned above, this study will quantify the effect of pore size on thermal conductivity through software simulations. Specifically, this study will simulate porous metal components with different pore sizes in Ansys to identify the optimal pore size that maximizes thermal conductivity efficiency. This study is of great significance for the design of cooling systems in various engineering applications, and can provide valuable insights for the development of more efficient heat dissipation technologies.

2. Methodology

2.1. Related Theory

The simulation involves some related theory, including the concept of heat flux. Heat flux refers to the rate of transfer of thermal energy across a given surface per unit time, measuring how much thermal energy moves through a particular area. Since this simulation deals mainly with conduction, the heat flux can be described by Fourier's Law (Eq1) [9]:

\( q=-k\frac{dT}{dx}\ \ \ (1) \)

where \( k \) is the conductivity of the material.

2.2. Model Construction

In the study, a piece of porous media is simplified into a cuboid with four cylindrical pores in fixed positions. The dimension of the cuboid is 1.4m*0.8m*1m. The diameters of the pores are then changed to different values during the process of simulation. Our final model is shown in Figure 1.

Figure 1. The geometry of model.

2.3. Material Settings

Structural steel, one of the most common ingredients in industries, is chosen to be the material of the porous media. Air is selected to be the fluid within the pores. Crucial thermal attributes of the two materials are listed in Table 1, including density, isotropic thermal conductivity and specific heat under constant pressure.

Table 1. Thermal attributes of the materials.

2.4. Boundary Conditions and Solution

Two essential boundary conditions (i.e. two different temperatures) are set on two opposite surfaces. The leftmost surface of the cuboid is set with a temperature of 300K, and its opposite surface is set with 500K as shown separately in Figure 2 and Figure 3. One of the edges between the surfaces is defined as the observed path as shown in Figure 4. The temperature and heat flux along the path can properly reflect the heat conduction situation inside the media. The model is solved to generate the temperature contour plot and the heat flux contour plot. The data of each node along the path is then accessible. A larger heat flux value can reflect a relatively better heat conduction efficiency. The process is repeated for four times with different pore diameter values of 0.05m, 0.15m, 0.3m and 0.4m to yield a trend.

Figure 2. The surface set with temperature of 300K.

Figure 3. The surface set with temperature of 500K.

Figure 4. The path defined in the simulation.

3. Results

For comparison, the temperature on each node is then put into Table 2 with separate columns for different pore diameters. Similarly, the data of heat flux on each node is put into another table, Table 3. To better contrast the results, line graphs for temperatures and heat flux are plotted separately with each colour indicating a different pore diameter using Python, as shown in Figure 5 and Figure 6. It can be noticed that the curvature of the temperature curve is prone to be more significant with the increase of pore diameter. The heat flux values tend to reach a peak when the nodes are around the location of the pores. It is worth to note that the value of the peak increases with pore diameter, indicating a better heat conduction efficiency. Figure 7 illustrates the 2D heat flux plots of one corner of the porous media in the four simulations.

Table 2. Node temperature values in the simulations.

Table 3. Node heat flux values in the simulations.

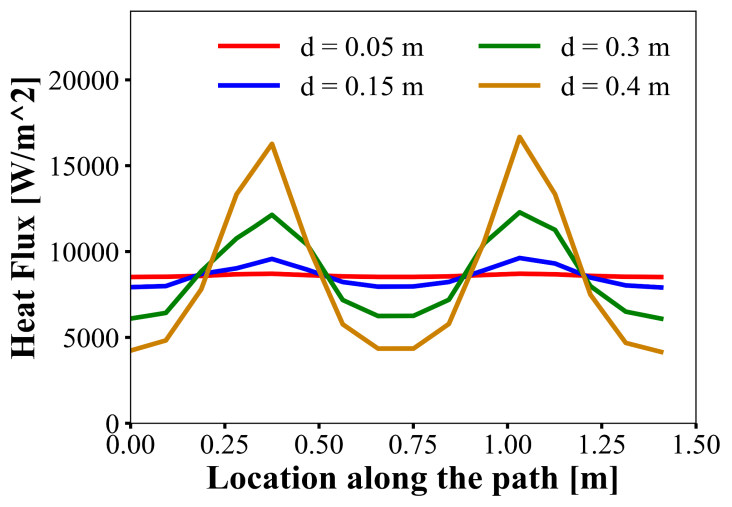
Figure 5. Heat flux vs Node location along the path.

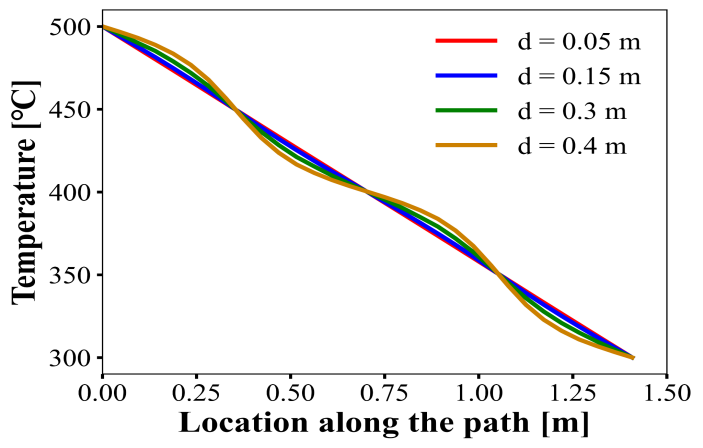
Figure 6. Temperature vs Node location along the path.

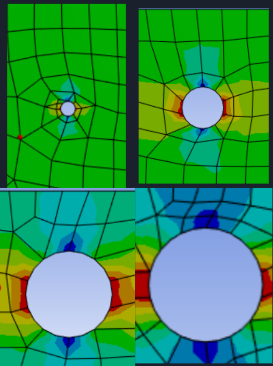
Figure 7. Four 2D temperature contour plots on the corners.

4. Discussions

The increase of temperature curve curvature with pore diameter can be explained by more significant heat flux fluctuation, given that the value of heat flux is proportional to the first derivative of temperature. Thus, when the overall slope of the heat flux curve increases, the rate of change of the temperature curve slope increases as well. The Maxwell-Eucken1 (ME1) Model [2] helps interpret better heat conduction efficiency with pore size. In ME1 Model, the effective thermal conductivity \( {K_{eff}} \) is given by the equation (Eq2):

\( {K_{eff}}= \frac{{k_{1}}{v_{1}}+{k_{2}}{v_{2}}\frac{3{k_{1}}}{2{k_{1}}+{k_{2}}}}{{v_{1}}+{v_{2}}\frac{3{k_{1}}}{2{k_{1}}+{k_{2}}}}\ \ \ (2) \)

In which \( {k_{1}} \) , \( {k_{2}} \) are the thermal conductivity of continuous phase and dispersed phase respectively and \( {v_{1}} \) , \( {v_{2}} \) are separately the volume of the two phases. In the data range of the simulation, the effective thermal conductivity \( {K_{eff}} \) tends to increase as the volume of continuous phase decreases and the volume of dispersed phase increases, resulting in higher heat conduction efficiency. An alternative interpretation is heating flux concentration, which can be concluded from the four 2D heat flux contour plots shown in Figure 7. Due to the increase of pore diameter, the edge of the porous media tends to be thinner, causing the heat flux to accumulate around that area. This study’s findings are further supported by recent research that emphasizes the critical role of pore scale in heat transfer within porous media. For instance, He et al. demonstrated that variations in pore size significantly impact thermal convection, suggesting that optimizing pore dimensions can enhance overall heat transfer efficiency within porous structures [10]. This aligns with the positive correlation observed in this study between pore diameter and thermal conductivity.

5. Conclusion

In this study, a porous model is set up, and the conduction is simulated using Ansys. Several conclusions can be made based on the results:

(1) Within the range involved in the simulation, as the diameter of the pores enlarges, the conductivity of the media increased.

(2) Considering the results and the interpretation of heat flux fluctuation and heat flux concentration, it can be anticipated that there is a positive correlation between the pore size and the thermal conductivity. Therefore, it can be further concluded that increasing the size of pores on certain cooling devices with porous plate do help transfer heat more efficiently.

(3) However, limitations of this investigation also exist, including overlooking the influence of porosity. This can be a focus for future studies in this field.