1.Introduction

Earthquake effects on arch bridges are profound, requiring in-depth examination to grasp and lessen possible harm. Present studies underscore the susceptibility of arc bridges to seismic events, though there are still voids in comprehensively grasping the dynamic interplay of earthquake dynamics with bridge constructs, particularly in the context of diverse soil conditions [1-4]. Even with progress in seismic engineering, the detailed impact of soil-structure dynamics on resonance events in arch bridges remains largely unexamined. This research fills this void by examining the oscillation properties of arch bridges when subjected to earthquakes, especially focusing on soil types [5]. The arched design of an arch bridge effectively converts upright loads into lateral push, rendering it naturally sturdy and apt for designs that resist seismic activity [6]. The resonance phenomenon, characterized by the alignment of earthquake wave frequency to the bridge's inherent frequency, may result in devastating collapses if not adequately comprehended and mitigated.

This document delves into the Bow Bridge in Central Park, using it as an example study. The design of the Bow Bridge's arch facilitates ideal movement of the load and enhances its structural firmness, rendering it a prime focus for research in vibrational impacts. Through thorough analysis of vibrations using computational models and real-world measurements, our goal is to identify areas susceptible and introduce specific design alterations to strengthen the bridge's earthquake resistance. This study is significant for its ability to enhance seismic design methods for arch bridges, guaranteeing their enduring stability, safety, and operational capability [7]. This research will enhance the understanding in the field of civil engineering, especially regarding seismic resilience, and offer actionable knowledge for the forthcoming design and upkeep of bridges.

2.Methodology

As a single-span arch bridge, the Bow Bridge has the longest span of 18 m and is 27 m in total length. The radius of the arch is 1.6 m. The main bridge structure is made up of cast iron, which was provided by the Bronx-based iron foundry Janes, Kirtland & Co. Material properties of components are given in Table 1. In the analysis of the bridge and its soil foundation, the obtaining of the soil beneath Central Park and the bridges’ cast iron material properties is complicated, so data was derived from an online database. Materials were defined using Engineering Data according to their corresponding densities, Young’s modulus, and Poisson’s ratios [8,9].

Table 1. Materials of the components.

The 3D models of the Bow Bridge with and without soil were constructed in Fig.1 and Fig.2 using SpaceClaim depending on the geometric and material properties obtained previously. Complex geometries like the classical Greek style decorations on the bridge deck were simplified to reduce computational cost while essential features like single span, the deck, and four bridge supports were retained.

Figure 1. The model of the Bow Bridge (without soil).

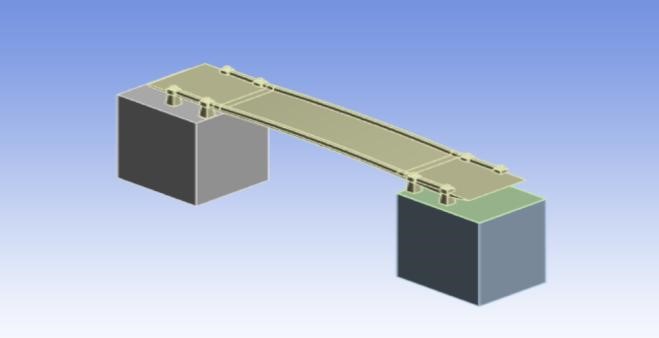
Figure 2. The model of the Bow Bridge (with soil).

In this analysis, the mechanical and meshing was used to obtain the corresponding natural frequencies and mode shapes under different vibration modes with and without the foundation of soil depending on the geometric and material properties of the bridge. Natural frequencies are the frequencies bridges or buildings can vibrate when subjected to certain external loads, while mode shapes suggest how structures respond when vibrating at corresponding natural frequencies.

2.1.Vibration of the Bow Bridge without soil

In the first group of analyses, the process chose the mesh size of 0.5m and the finite element shape of the tetrahedron. As for boundary conditions, all eight bridge supports and two shorter sides of the bow bridge are fixed. The finite element model of the Bow Bridge without soil is shown in Fig.3.

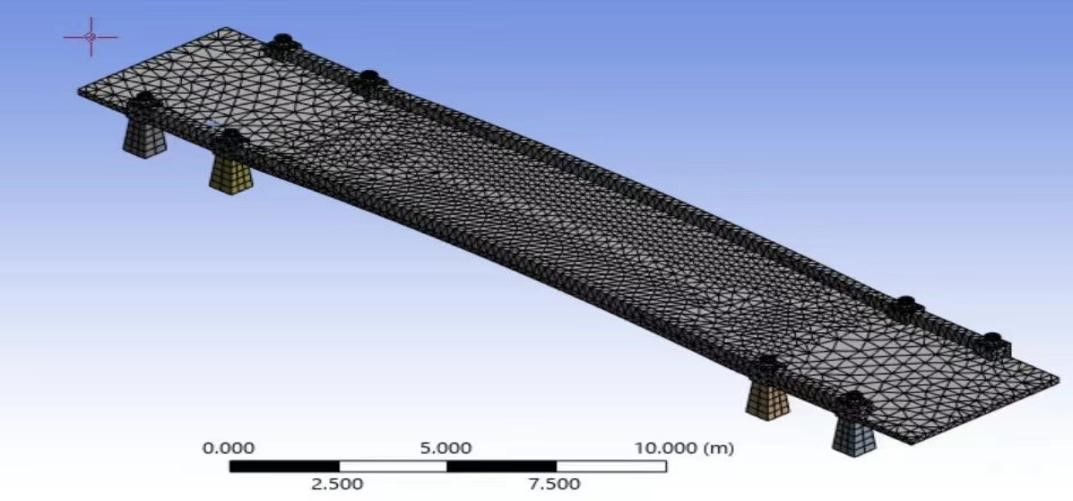
Figure 3. Finite element model of the bridge (without soil).

2.2.Vibration of the bridge with soil foundation

In the second group of simulation, the same mesh size and finite element shape as the first group were chosen. As for the boundary conditions, the bottom & 4 surrounding sides of each soil part are fixed to simulate real-world constraints. The finite element model of the Bow Bridge without soil is shown in Fig.4.

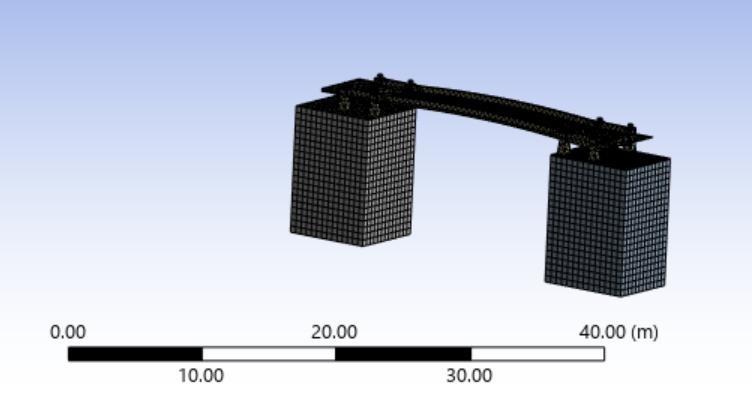
Figure 4. Finite element model of the bridge (with soil).

In the two groups of analysis, the vibrations are both simulated under 6 different vibration modes. The mode shapes and natural frequencies were then extracted for further comparison and analysis [10].

3.Results

The natural frequencies in the soil-less group and the soiled group were plotted as shown in Fig.5 and Fig.6. Comparison between the two types of natural frequencies and values calculated, the vibration frequency of the soil-less group is much higher than the soiled group.

Figure 5. The line chart of the natural frequencies (without soil).

Figure 6. The line chart of the natural frequencies (with soil).

The corresponding mode shapes in each group were obtained, as depicted in Fig.7 and Fig.8. The six modes of the seismic waves exhibit a gradual increase in frequency, reflecting the vibrational characteristics of the bridge. For the soil-less group, frequencies of 8.7491HZ, 18.195HZ, and 31,754HZ (modes 1,3,5) correspond to an up-and-down vibration direction; while frequencies of 38.342HZ and 12.96HZ (modes 2,6) indicate lateral extension and contraction vibration modes. Additionally, at a frequency of 28.315HZ, the bridge exhibits multiple directional extensions combining both types of vibration modes.

Figure 7. Vibration modes (without soil).

In Fig .8, vibration frequencies of 2.717Hz,3.4183 Hz, 4.4619Hz, and4 .951 HZ (modes1 ,2 ,4 ,5 ) result in an up-to-down mode shape; whereas frequencies of3 .4437 HZ and5 .2319 HZ lead to twisting mode shapes.

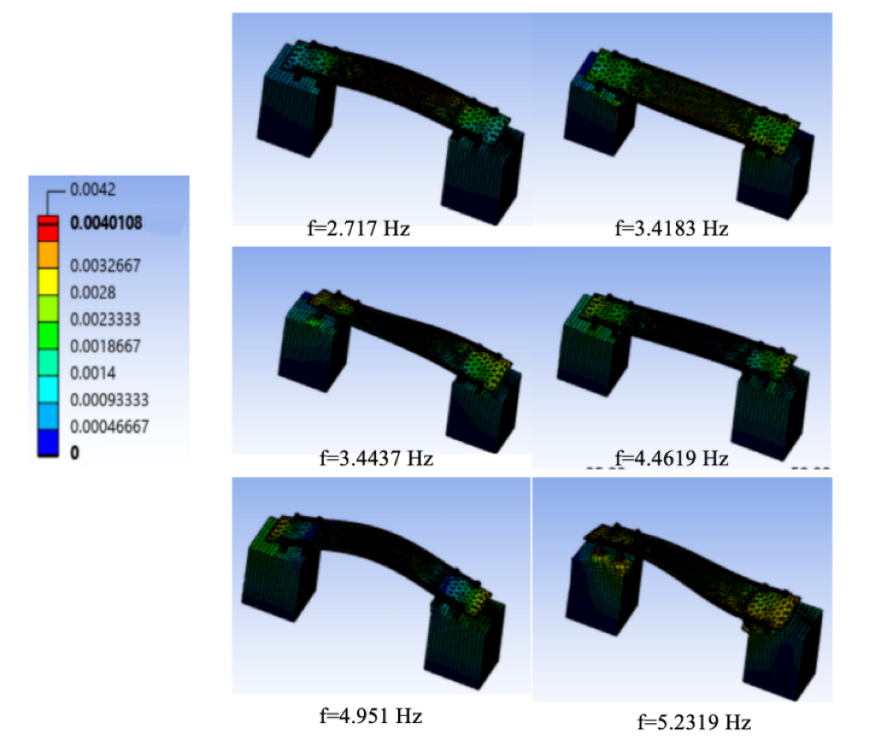
Figure 8. Vibration modes (with soil).

Obviously, the overall vibration amplitude of the soiled group is much smaller than the soil-less group, as the testing in six modes separately [9].

4.Discussion

Based on the two foundations, it can be observed that the soil foundation exhibits significantly lower vibration levels compared to the soil-less foundation. The inclusion of both soil and four-column stone boundaries in the soil foundation results in a larger overall mass, thereby enhancing global structural stability. Moreover, this approach aligns more closely with real-life scenarios, which are in an environment with soil. Method Select Finite element analysis serves as a fundamental method for studying and calculating numerical values related to building structures offering versatility in application while providing flexibility for analyzing complex structures under various conditions ANSYS has been utilized within this research study due to its range of capabilities suitable for such analyses. Furthermore, additional limitations and challenges in this research warrant further investigation. The simulation process does not account for various natural influences such as temperature, bearing capacity, and material properties. Reference Study This research lacks the study of the real environment, which should have the soil variable. Studies on soil–structure interaction considering the effects of soil heterogeneity have been presented by Breysse et al. The results showed the effect of soil variability on the induced forces in a linear mechanical system. They developed a coupled reliability–mechanical approach to study the effect of soil–structure interaction for RC bridge, which differs little from the Bow Bridge on materials. Also, they analyze the reliability of the research, by using the First Order Reliability Method implemented. Each new point in the iterative process, the ultimate moments in the girder cross-sections are computed for the load cases at the ULS, by using the numerical model developed under MATLAB, in which the soil–structure interaction is appropriately considered. The procedure includes two iterative loops: one for the nonlinear mechanical analysis and the one for the First Order Reliability Method (FORM). The result leads to the failure probability of the considered cross-sections as well as the importance factors regarding various random variables.

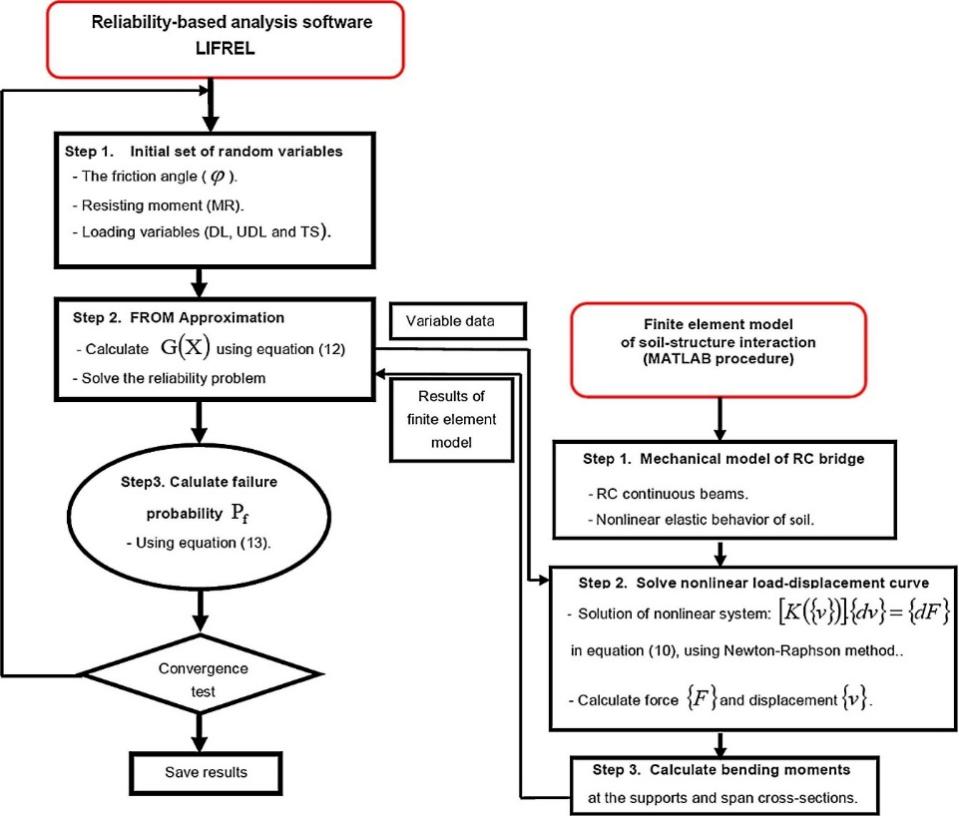
Figure 9. The reliability study flow chart.

According to the reference, the obtained results show that soil variability plays an important role in the behavior of soil–structure in RC bridges, which can also be used in the study of the iron bridge (see Figure 9). Finally, a parametric study showed the large effect of soil–structure interaction on the bridge reliability, especially when the soil nonlinearity is considered. Although the material and properties of the two bridges are different, the soil structure is necessary for studying to approach the real situation. [10].

5.Conclusion

This article conducted finite element modeling, modal testing, and finite element model updates on the arch bridge. A three-dimensional finite element model of the bridge was established, and its dynamic characteristics were theoretically analyzed. Under environmental excitation such as whether there is soil from the tests. In modal testing, various human or natural factors are considered to simulate the external forces acting on the bridge in real situations as much as possible and to achieve the most accurate, reasonable, and realistic modal.

(1)From the soil-less environment, in the first three modes, the frequency is below 20 Hz, while in the last three modes, it is above 25 Hz, and the overall frequency trend shows an increasing trend. This is a very high resonance value.

(2)From the soiled environment, the frequencies of the six modes are far less than ten hertz, and even below 6 hertz. Compared to a soil-less environment, this is a very small and safe value that can ensure that the bridge will not be damaged due to resonance

(3)Comparing the two groups of results, it can be found that the average vibration frequency in soil environments is much lower than that in non-soil environments, which intuitively and proves the influence of soil environment on bridge vibration frequency. Therefore, environmentalists pay attention to the soil environment around the construction of bridges to protect the bridges and pedestrians.

Acknowledgment

Sitong Chen and Yuxi Yang contributed equally to this work and should be considered co-first authors. Hao Li and Siqiao Wang contributed equally to this work and should be considered co-second authors.