1. Introduction

The brain computer interface (BCI) concept was first proposed in 1973. This technology involves the establishment of a direct connection between a computer and the brain of a human or animal, creating a communication and control system that bypasses traditional muscle and nerve pathways [1]. Following its initial proposal, BCI technology underwent extensive development without any breakthroughs for an extended period. Nevertheless, it was not until the 1990s that significant progress was made, driven by advances in computer science, neurology, and brain research. This technology has made significant advances in several fields, including clinical medicine, neurorehabilitation, art, and entertainment. BCI systems can be classified according to the methods employed for acquiring signals, namely non-invasive and invasive systems. Non-invasive systems offer a resolution of approximately 0.05 seconds and 1 millimeter, while invasive systems provide a much finer resolution of about 0.003 seconds and 0.05 millimeters [2], as detailed in Sections 2.1 and 2.2. However, in the development of BCI technology for many years, the processing of noise and artefacts has been a major difficulty, this paper will use literature analysis and other methods to study Noise and artefacts in EEG signals are processed using the DCCRN-LSTM algorithm to preserve privacy and enhance valid information in EEGs, which can reduce the interference of noise for the effective information in EEG and provide a potential noise reduction method for the field of EEG analysis. This study focuses on EEG noise reduction technology based on DCCRN-LSTM. For evaluating related articles the criterion was the relevance of EEG and DCCRN-LSTM to this paper, which are the key areas of concern in this thesis.

2. Classification of BCI systems based on different ways of acquiring signals

2.1. Invasive Method

Invasive BCI involves the placement of electrodes directly into the brain. This approach offers higher temporal and spatial resolution than non-invasive methods. However, it typically necessitates a craniotomy, which involves the removal of a portion of the skull, the placement of the electrodes or probes onto the cerebral cortex, and then the restoration of the skull. Consequently, invasive BCI is more expensive and carries greater risks, including the potential for infection and the degradation of recorded signals over time.

2.2. Non-Invasive Method

Typical non-invasive technologies include Near-infrared Spectroscopy (NIRS), Magnetoencephalo-graphy (MEG), Functional Magnetic Resonance Imaging (fMRI), and EEG. While non-invasive brain-computer interfaces (BCIs) offer lower temporal and spatial resolution than the invasive method, they do not require surgical implantation. Instead, they can be easily implemented using a headband or hat, making them cost-effective and relatively safe. By placing electrodes on the scalp and applying conductive gel, or using headgear to secure the electrodes and directly record neural signals, these systems provide the benefits of affordability, ease of operation, and safety [3]. Consequently, non-invasive BCI technology is widely adopted and utilized. The Electroencephalogram (EEG), is a technique that captures electrical impulses produced by brain neurons by placing electrodes and other electronic components on the scalp [4]. However, EEG signals are frequently susceptible to a variety of disturbances, including those resulting from human physiological processes or non-physiological sources, such as mechanical equipment. The nonlinear, random, non-correlated, and non-Gaussian characteristics of EEG signals render the effectiveness of traditional wavelet transform or filter methods in eliminating these interferences severely limited. In order to address this challenge, deep learning-based methods have demonstrated significant potential in the realm of noise reduction. This article presents a novel approach that employs a combination of DCCRN and LSTM to mitigate EEG noise.

3. Key algorithms for noise reduction and EEG enhancement

3.1. LSTM

Long Short-Term Memory (LSTM) is a framework derived from RNN (Recurrent Neural Networks) [5]. In traditional RNNs, connections are typically established between hidden layers, with the input to a hidden layer including both the output from the input layer and the output from the hidden layer at the previous time step. While RNNs offer advantages in analysing time series data, they frequently encounter issues such as long-term dependency problems, gradient vanishing, and gradient explosion [6]. LSTM effectively addresses these challenges by preserving long-term sequence information and mitigating the issues of gradient vanishing and explosion. Compared to the AutoRegressive Integrated Moving Average (ARIMA) time series model, LSTM is more adept at handling complex time series prediction tasks, particularly those involving long-term dependencies.

The fundamental gate mechanism of LSTM comprises the input, forget, and output gates. The introduction of the forget gate enables LSTM to retain information over extended periods. Upon receipt of a novel input, LSTM combines the input with the output from the preceding time step to generate a distinct vector. Subsequently, the aforementioned vector is subjected to a sigmoid neural layer. If the value is close to 0, the component information has been “forgotten.” Conversely, a value close to 1 indicates the retention of complete memory. This principle is exemplified by the following formula.

\( {f_{t}}=σ({W_{f}}\cdot [{y_{t-1}},{x_{t}}]+{a_{f}})\ \ \ (1) \)

Where \( {f_{t}} \) represents the decision vector of the forget gate, \( σ \) , \( {W_{f}} \) , respectively represent the sigmoid activation function and the weight of the forget gate of dimension \( {d_{c}}×({d_{x}}+{d_{h}}) \) ; \( {y_{t-1}} \) , \( {x_{t}} \) are the output at time t-1 and the input at time t; \( {a_{f}} \) represents the offset of the forget gate.

The output value of the current LSTM is:

\( {y_{t}}=tanh{({C_{t}}*{o_{t}})} \ \ \ (2) \)

\( {C_{t}} \) represents the new cell state, \( {o_{t}} \) represents the decision vector of the output gate.

\( {i_{t}}=σ({W_{i}}[{y_{t-1}},{x_{t}}]+{a_{i}})\ \ \ (3) \)

\( {\bar{C}_{t}}=tanh{({W_{c}}[{y_{t-1}},{x_{t}}]+{a_{c}})}\ \ \ (4) \)

In equations (3) and (4), \( {i_{t}} \) represents the decision vector of the input gate, and \( {\bar{C}_{t}} \) represents the candidate information.

\( {C_{t}}={\bar{C}_{t-1}}*{f_{t}}+{\bar{C}_{t}}*{i_{t}}\ \ \ (5) \)

\( {o_{t}}=σ({W_{o}}[{y_{t-1}},{x_{t}}]+{a_{o}})\ \ \ (6) \)

In the context of EEG denoising, the LSTM model can learn features from long time series data. During training, the LSTM model utilises the learned features and patterns to effectively denoise the EEG signals. The LSTM model can predict and remove noise components from the EEG data, thereby improving the signal-to-noise ratio.

3.2. DCCRN

Machine learning models are typically classified into time series models and regression models. In the context previously outlined, the LSTM model is employed due to its capacity to learn features from long time series data. Consequently, this section employs a time series model for modelling purposes. The Deep Complex Convolution Recurrent Network (DCCRN) is a network model that combines the structures of Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), and Long Short-Term Memory (LSTM) to address the issue of time series dependencies. It is distinctive in that it incorporates complex convolutional layers and LSTM layers. The complex network is capable of capturing the correlation between amplitude and phase angle through complex multiplication, thereby enabling a more comprehensive representation of signal characteristics [7].

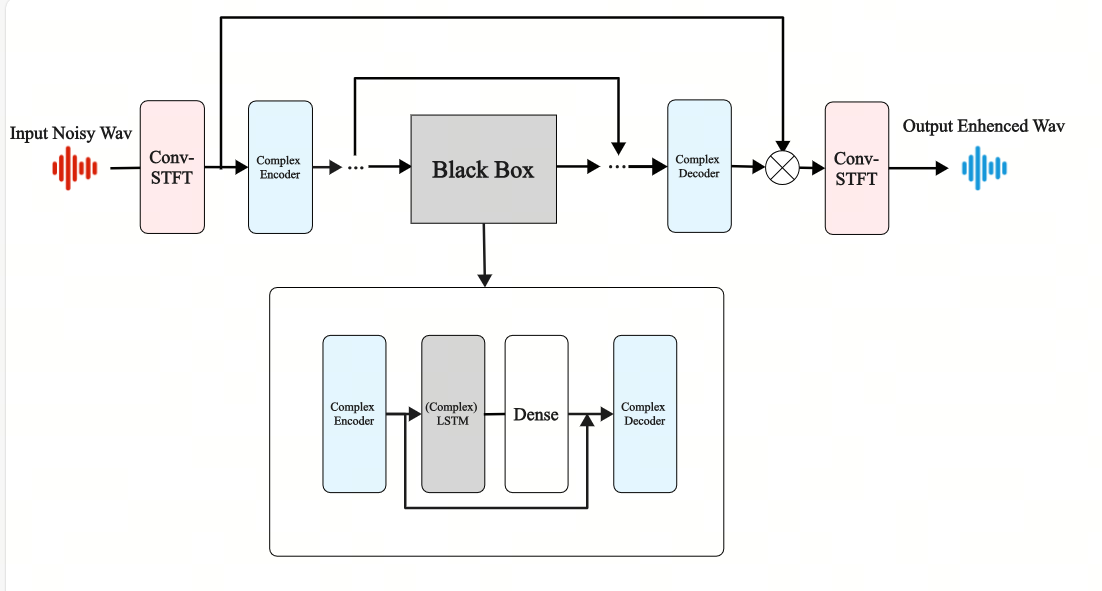
Figure 1. DCCRN Flowchart

The encoder/decoder block comprises a complex two-dimensional convolutional neural network (Conv2d), batch normalization, and a real-valued parametric rectified linear unit (PreLU) [8]. The complex-valued convolution filter \( K \) can be represented as \( K= {K_{r}}+j{K_{i}} \) , where \( {K_{r}} \) is the real part of the complex convolution kernel, and \( {K_{i}} \) is the imaginary part of the complex convolution kernel. The input complex matrix \( M \) can be expressed as \( M= {M_{r}}+j{M_{i}} \) . In conclusion, the complex output expression is derived through the operation \( X⊗W \) , as illustrated in Equation (7).

\( {F_{out}}=({M_{r}}*{K_{r}}-{M_{i}}*{K_{i}})+j({M_{r}}*{K_{i}}+{M_{i}}*{K_{r}})\ \ \ (7) \)

In formula (7), \( {F_{out}} \) denotes the output feature of one complex layer.

According to the real part \( {M_{r}} \) and imaginary part \( {M_{i}} \) of the complex input, the output \( {F_{out}} \) of the complex LSTM can be expressed as:

\( {F_{rr}}={LSTM_{r}}({M_{r}});{F_{ir}}={LSTM_{r}}({M_{i}})\ \ \ (8) \)

\( {F_{ri}}={LSTM_{i}}({M_{r}});{F_{ii}}={LSTM_{i}}({M_{i}})\ \ \ (9) \)

\( {F_{out}}=({F_{rr}}-{F_{ii}})+j({F_{ri}}+{F_{ir}})\ \ \ (10) \)

\( LST{M_{r}} \) and \( LST{M_{i}} \) represent the real and imaginary parts in the traditional \( LSTM \) model, while \( {F_{ri}} \) represents the result calculated by \( LST{M_{i}} \) and input \( {M_{r}} \) .

The original design of DCCRN was intended for speech enhancement tasks, with a particular focus on phase-aware speech enhancement. Although DCCRN was not initially designed for EEG noise reduction, its deep learning capabilities and complex number processing offer a promising potential solution for this application. Nevertheless, further research and experimental validation are required to ascertain the efficacy of this approach in EEG noise reduction. In particular, the application of complex number processing to EEG data, along with the adjustment and optimisation of the network structure, necessitates further extensive exploration and investigation.

3.3. Section summary

As a recurrent neural network structure, LSTM is particularly adept at processing time series data and capturing long-term dependencies. In EEG signal processing, LSTM is an effective tool for modelling complex patterns in time series. This is crucial for noise reduction tasks due to the presence of helpful information and noise in EEG signals over extended time scales. In contrast, DCCRN has been developed for the specific purpose of processing complex-valued data. It offers the advantages of low training parameters and computational costs and does not require prior knowledge. In the context of EEG signal processing, the use of complex-valued operations enables the capture of both amplitude and phase information, which is of particular importance in retaining key features within the signal and in the removal of noise. The integration of LSTM and DCCRN within an algorithm has the potential to enhance noise reduction efficiency, resulting in reduced computing time and resource consumption. The long-term dependency capture capability of LSTM, when combined with the complex value operation processing capability of DCCRN, results in a synergistic effect, enabling the algorithm to more effectively identify and separate noise components in EEG signals, thereby improving the overall noise reduction effect. The principles, advantages, and disadvantages of various algorithms are presented in Table 1.

Table 1. Principles, advantages and disadvantages of various algorithms

4. Conclusion

This paper reviews EEG denoising technology based on the DCCRN-LSTM model. The LSTM’s ability to mitigate gradient explosion and vanish with the DCCRN’s strengths in complex-valued operations enables the effective processing of various noise components in EEG signals. The successful application of this technology can significantly enhance the quality of EEG data, thereby improving the accuracy and robustness of signal processing. Although DCCRN is currently primarily employed in speech denoising, it introduces novel concepts and methodologies to EEG signal processing. However, the method mentioned in this paper still has some shortcomings. The DCCRN-LSTM algorithm is not widely used in the field of EEG, so the method may have poor performance for certain types of signals and noise in EEG, which needs to be optimised and improved after further use and observation of the model, and there is also some room for improvement in the large computational complexity of the model. Future research will focus on optimising the model structure and parameters of the DCCRN-LSTM model to improve its performance in EEG noise reduction, followed by further investigation of the possibility of combining it with other algorithms to enhance the noise reduction effect. In addition, the application of this algorithm in other fields needs to be explored to increase its wide range of applications. By addressing these limitations of the DCCRN-LSTM model, and for future focused directions, the model has great potential in the field of EEG noise reduction, which will improve the processing capability of EEG signals and provide a potential solution to the noise reduction problem for more directions.