1. Introduction

The SARS virus is β Coronavirus belonging to subgroup B. The World Health Organization announced on April 16, 2003 that the variant of coronavirus was officially confirmed as the pathogen causing SARS. Although this coronavirus variety is related to the influenza virus, it is substantially different. It has never been identified in humans. The SARS virus is what researchers gave it.

The acute respiratory infectious disease caused by the SARS coronavirus is named “severe syndrome of acute respiratory distress” by the World Health Organization and “SARS” in China. The SARS virus can be transmitted through short-distance droplets, aerosols, or contaminated objects. At room temperature of 24 ℃, the virus can survive for at least 10 days in urine, more than five days in sputum and feces of diarrhea patients, and 15 days in blood. The virus may stop being contagious after being exposed to commonly used disinfectants and fixatives, and the virus can be inactivated in 90 minutes above 56 ℃. This paper aims to find out how the SARS virus spreads, and also compares the SARS virus to the novel coronavirus. In the whole study, the author will use the SIR model and the SIERP model. It also combines specific cases of specific cities [1].

2. The SARS virus

2.1. Introduction to SARS virus and RNA virus

The SARS virus is an RNA virus. The spike protein, membrane protein, nucleocapsid protein, envelope protein, and RNA make up the SARS virus. SARS coronavirus is when the body has a continuous high fever above 38 degrees. At the same time, there will be headaches, fatigue, joint pain, dry cough, and other symptoms. If the symptoms are severe, it will lead to dyspnea, aggravation of cough symptoms, and even shock.

RNA viruses have two replication modes: Reverse transcription and self-replication. The error-repair mechanism's enzyme activity is so low and nearly nonexistent during viral RNA replication that it rapidly mutates. Vaccines are difficult to develop because they are based on a fixed gene or protein of the virus. Compared with DNA viruses, RNA viruses are more likely to cause disease, deadlier to their hosts, more likely to mutate, and therefore more diverse, harder to develop effective vaccines, and harder to prevent. RNA viruses are generally less resistant than DNA viruses and are easier to cure. But there are exceptions. For example, double-stranded RNA viruses are very resistant, and retroviruses are extremely difficult to cure. In epidemiology, we often use an index R0 (basic infection number) to evaluate the infectivity of a disease, that is, how many people will be infected by an infected person on average [2]. If the R0 value is larger, it means that the disease is more infectious. SARS virus’ R0 is very large.

Figure 1. RNA structure [3].

The species, strain, dose, route of infection, type of host, and immune status of the SARS virus are related to each other. It was found that its s glycoprotein played a key role in the pathogenesis of the virus. The importance of the S protein in pathogenesis lies in its function of mediating virus entry into target cells and viral spread. At the same time, the S protein also plays an important role in the process of inducing an immune response to viruses. For instance, it is an induced protein that triggers host cell immunity and serves as a target for antibodies that can neutralize it. In addition, it was also found that the transmission of MHC class I molecules and other proteins in infected host cells was inhibited to some extent, and some factors related to inflammation were also found. Including tl-tb Clonal stimulator I receptor and tnf-a mRNA expression were up-regulated.

2.2. The source of SARS virus

There is no connection between the SARS virus and pets, cattle, or poultry. The Ministry of Agriculture's animal coronavirus epidemic focus investigation team gathered 1700 animal samples from 59 species, mostly from different cattle, poultry, wild animals, aquatic creatures, and pets that have or may have human interaction. Coronavirus genes have been found in a variety of wild species, including snakes, bats, monkeys, civets, and monkeys. The viral gene sequence that was discovered is perfectly compatible with the SARS virus. Therefore, the investigational team speculates that some wild animals may harbor the SARS virus or a coronavirus that is similar to SARS [1].

2.3. The treatment of SARS virus

In addition, there is no specific treatment for SARS. But most patients can be cured. Although there are no specific anti-SARS coronavirus drugs, some antiviral drugs will be selected for clinical trials. The focus of patients' treatment is to strengthen support for symptomatic treatment, such as antipyretic fluid replacement, nutritional support, and other treatments [4]. Most patients need oxygen therapy. According to the degree of hypoxia, patients should be treated with nasal catheter oxygen inhalation, face mask oxygen inhalation, or even ventilator-assisted breathing, to prevent corresponding complications, especially to prevent possible mixed infection, and use corresponding anti infection drugs when necessary. It is through respiratory droplets, direct contact, and other ways to spread. Therefore, a surgical mask or N95 mask should be worn, especially in crowded places. The patient's sputum and secretions should be disinfected and not spit randomly. Items used by the patient should also be disinfected by spraying with 75% alcohol or the chlorine-containing disinfectant. Healthcare workers should wash their hands immediately after encountering patients or their secretions.

It can provide a reference for the treatment and prevention of novel coronavirus. It can deepen people’s understanding of RNA viruses so that we are less afraid of RNA viruses. At the same time, by studying the relevant characteristics of RNA viruses, we can better understand the coronavirus now raging in the world, which is a very meaningful thing. In addition, RNA viruses are easy to mutate, so we must strengthen their prevention, and we need to invest more time in the development of vaccines.

3. Mathematical models

3.1. SIR model and SEIRP model

In this paper, we are going to apply the Mathematical model to access the SARS transmission. I used the SIR model. This model enables us to have a clearer understanding of the spread of viruses.

First, Think of a sickness that, if treated, results in immunity (which contains fatalities There are still dead people being tallied). (1) We assume that there is no entry into or departure from the population. (2) A patient must have a particular level of infectiousness in order to infect someone aft er they come into touch. Suppose that the number of susceptible persons that a patient can infect is directly proportional to the total number of susceptible person s (T) in this environment in the unit time of time t, and the proportion coefficient is β, So the number of people infected by all patients in unit time at time t is β s(t) i(t). (3) at time t, the number of people removed from infected persons per unit time is proportional to the number of patients, and the proportion coefficient is γ， The number of movers per unit time is γ i(t) (These are very important conditions). Then we can get the equations.

\( S(i)+I(J)-→I(i)+I(j) \)

Secondly, the population is divided into three groups. S, who have the disease and can spread it; the infectives, I; and the removed class, R, which consists of those who have either had the sickness or are immune, recovered, or secluded till recovering.

Thirdly, the progress of individuals is schematically described by S → I → R.

Fourthly, let S(t), I(t), and R(t) represent the total number of members in each corresponding class at time t. Notably, just R(t) is typically known. It is frequently believed that R(t) represents the total number of patients admitted to hospitals.

Then we can get the module equations and charts.

\( \frac{ds(t)}{dt}=-Bi(t)s(t) \)

\( \frac{di(t)}{dt}Bi(t)(t)-ri(t) \) [5]

\( \frac{dr(t)}{dt}=ri(t) \)

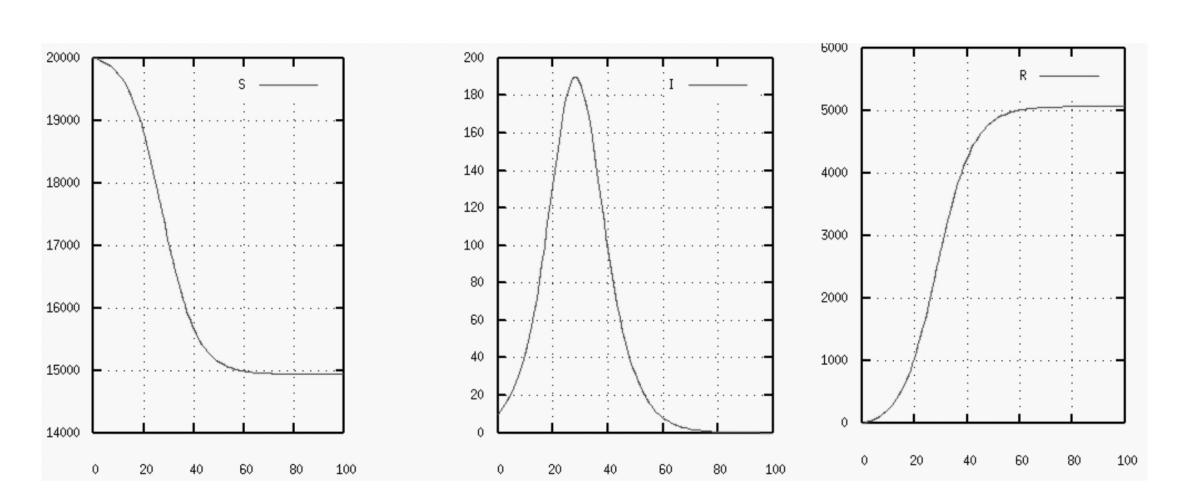
Figure 2. SIR mathematical model [6].

R increases monotonically until the limiting value R is reached, S declines monotonically from its starting value to its end value. Both curves feature two separate eras when the reduction (or rise) either decreases (or increases) exponentially slowly or exponentially quickly.

Solving S(T) and I (T) is quite tough.The properties of solutions I (T) and S (T) can be discussed by using phase trajectory analysis, and the change curve is shown in Figure 3. The arrow indicates the changing trend of S (T) and I (T) with the increase of time t.

Figure 3. The mathematical model established by the Institute [7].

\( σ=\frac{β}{γ} \)

In order to prevent the transmission of infectious illnesses, it is required to meet the following requirements \( {S_{0}} \lt \frac{1}{σ} \) .

This goal can be achieved by improving the medical level or by mass immunization.

Then the author used the SEIRP module.

This new model, which is a modification of the conventional SIR, will be known as the SEIRP model (where E refers for the Exposed class and P represents for protection).

We suppose that two groups of sick people are dispersed over a sizable population. Virus A infects one group while virus B infects the other.

Six different classes can then be created from the population.

When the infectious time is complete, the individual enters the Removed class R, which is made up of persons who have either recovered from sickness A, are immune to the illness, or have been quarantined until they are. A susceptible who contracts illness B initially will move into the infectives class IP before moving into the removed class RP.

The author eventually obtained the module equations and graphics.

Figure 4. Diagram of each part.

\( \frac{dS}{dt}=-rS(t)I(t)-{r_{p}}S(t){I_{p}}(t) \)

\( \frac{dE}{dt}=rS(t)I(t)-bE(t) \)

\( \frac{dI}{dt}=bE(t)-aI(t) \)

\( \frac{dR}{dt}=aI(t) \)

\( \frac{{dI_{P}}}{dt} \) = \( {r_{P}}S(t){I_{P}}(t) \) - \( {a_{P}}{I_{P}}(t) \)

\( \frac{d{R_{P}}}{dt}={a_{P}}{I_{p}}(t) \)

3.2. Application of SEIRP model

The SEIRP model [6] will then be used by the author to analyze the SARS outbreak in Hong Kong. The author wants to explain how huge localized occurrences in a number of hospitals and the Hong Kong housing complex Amoy Gardens were superimposed on a background infection level that was more or less consistent for a significant amount of time. The majority of the daily new confirmed cases from the community stayed between 15 and 25 if we just take into account the number of verified SARS patients from the Amoy Gardens and those from the adjacent hospitals aren't included, then those SARS cases from the neighborhood (Naturally, this number decreased as the Hong Kong authorities enforced stringent confinement directives) [6].

First, we suppose that IP (0) = 0.5 million, meaning that 0.5 million residents of Hong Kong have the illness B. We assume that sickness B is brought on by a gastro-enteritis virus, which is often quite infectious, therefore this supposition is fairly logical. We use the assumption that S(0) = 6.8 - 0.5 = 6.3 million since Hong Kong has a population of roughly 6.8 million. Then, we make the rather arbitrary assumptions that E(0) = 100 and I(0) = 50. With these starting circumstances, we attempted to use a gradient-based optimization approach to get the parameter values. If we use the parameter values r = 10.19 10-8, RP = 7.079 10- 8, a = 0.47, aP = 0.461, and b = 0.103, the outcome is that the curve for R closely matches the total number of verified SARS cases that have been detected in the community [6]. The predicted outcomes are congruent with the reality as shown by the accompanying figures. Our model is therefore workable.

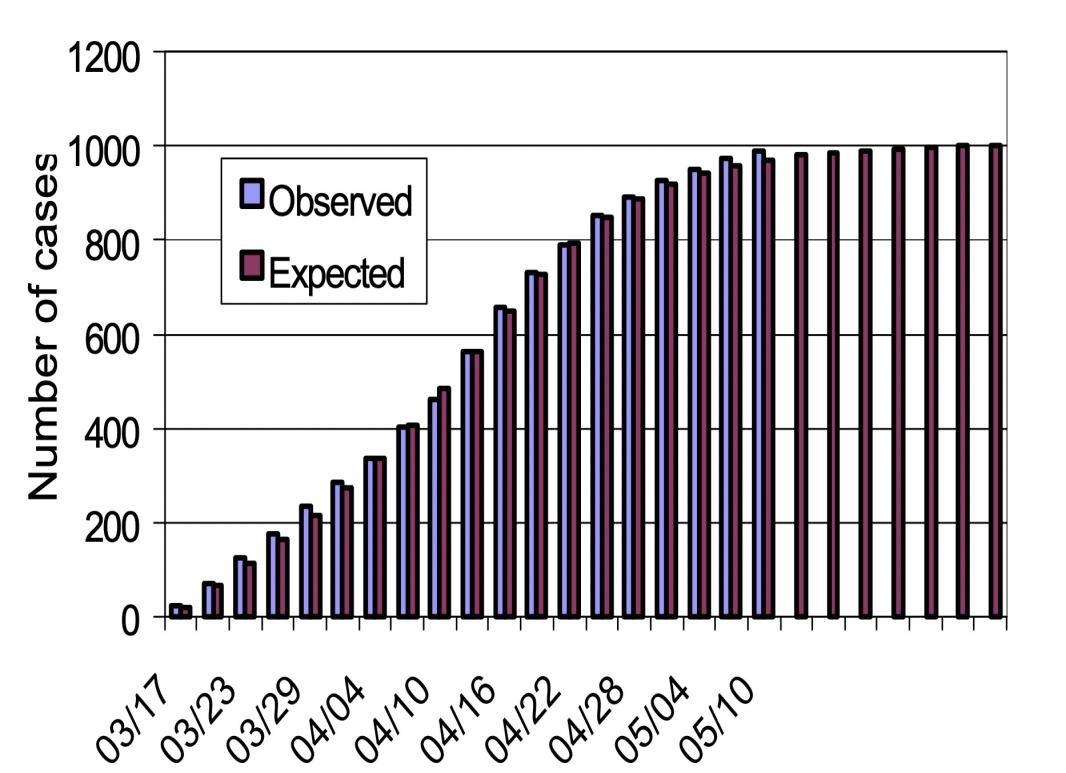
Figure 5. Relationship between time and quantity [6].

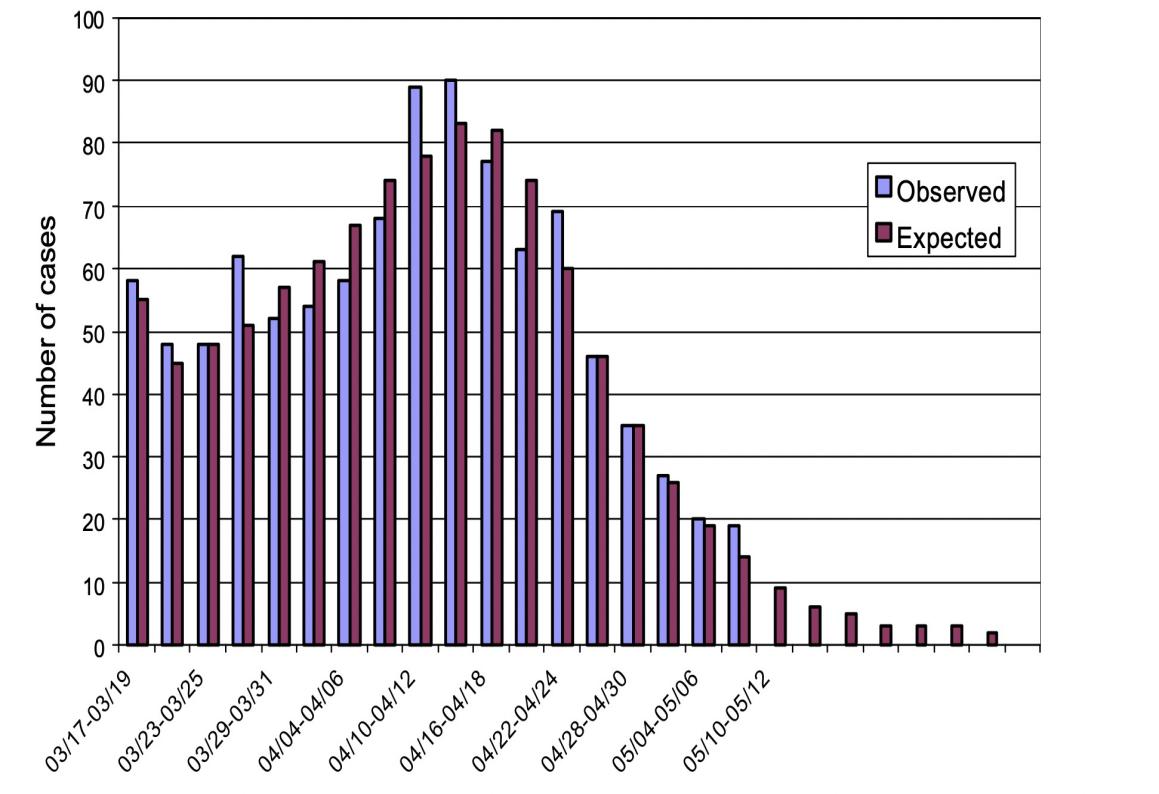
Figure 6. Relationship between time and quantity [6].

4. Discussion

It can be seen from the above figure that the expected results are consistent with the actual situation. Thus, our model is feasible.

The first epidemic of the twenty-first century is a severe acute respiratory syndrome. If it will resume in the fall of 2017 is unknown. To combat the epidemic, cut its duration as much as possible, and get ready for more or less comparable outbreaks in the future, we must combine a variety of approaches. The mathematical model in this situation may perform several different tasks. Mathematical models can be well combined with biological research. Now we are also facing the test of COVID-19, and we can also study it through mathematical models. The differential equation-based SIR model can properly fit the curve to the data at hand and apply phase trajectory analysis to determine the appropriate steps to stop the spread of infectious illnesses. The theoretical foundation is adequate.

However, the model's population categorization is not sufficiently precise, and the isolation component is not explicitly taken into account. Actually, the best strategy to stop the disease from spreading is to isolate suspicious patients. The model makes no mention of a feedback system. Simply projecting the data outward over a very long time based on the current data will surely result in a reduction in accuracy. Additionally, the model's resilience is significantly impacted by how challenging and sensitive to the starting values the differential equations are to solve.

From the analysis of the model, we can see that we can prevent and control SARS virus through mass immunization or by improving the medical level, which also provides us with the Enlightenment on the prevention and control of novel coronavirus. At the same time, pharmaceutical chemists have made unremitting efforts in the process of screening anti SARS drugs, but so far, people have not developed anti SARS drugs with high efficiency, less side effects and low toxicity, which has posed a challenge to pharmaceutical chemists.

The natural science foundation of China also launched three research projects on SARS prevention and epidemiology, including five immunological studies on epidemic diseases and four basic studies on vaccine development. Therefore, the research and development of anti-SARS drugs will be much faster than the previous anti-SARS medication development and research. It is believed that the research and development of anti SARS drugs will achieve fruitful results in the near future. Viral infectious diseases such as sars HIV. HBV and HCV are increasingly threatening human health. Through the research on vaccines against the SARS virus and various natural and synthetic drugs, they will get more methods to fight with COVID-19.[8]

There are several significant variations between SARS-CoV-2 and SARS-CoV, despite certain molecular, epidemiological, and clinical similarities. The two viruses' gene sequences are the primary distinction between them. Second, a total of 8422 people globally contracted the SARS-CoV during the pandemic; 919 of them passed away, representing a mortality rate of 9.5%. A total of 5328 individuals in China were infected with the SARS-CoV, and 349 of them passed away, representing a 6.5% fatality rate. There were 72,436 confirmed cases of 2019-nCoV in China as of February 17, 2020, with a mortality rate of 2.6% and 1868 fatalities [9]. SARS-CoV-2 has a higher number of confirmed cases, suspected cases, and fatalities than SARS, but its fatality rate is lower.

Further, promote the scientific process of the pathogenesis of viral diseases and effective drug prevention and treatment. Recently, many coronavirus infections have been reported in the newspapers. How to completely inhibit this kind of virus is a problem that many modern researchers have to face. In the near future, a large number of scholars and professors will be involved in research on this subject [10].

5. Conclusion

Thanks to the unity and unremitting efforts of all sectors of society, people finally defeated the SARS virus. In addition, based on the establishment of the model and the analysis of specific cases, it is concluded that COVID-19 can be responded to by either mass immunization or improving the level of public health care. In addition, we have a further understanding of the mode of transmission of SARS and the means of prevention and control. The society should increase the investment in medical facilities to resist the attack of COVID-19 and prepare for any possible virus attack in the future. Because the novel coronavirus is mutating and the number of infections continues to increase, it is difficult to use mathematical models for predictive analysis in this paper at this time. Future studies can use mathematical models to analyze this novel coronavirus.