1. Introduction

Rubik's Cube, as one of the most popular and popular educational toys in the world, has been sought after by countless people. Every year, the world holds Rubik's Cube races or various pattern challenges. The playing method of the Rubik’s Cubes itself is also very attractive. By restoring the disturbed Rubik’s Cubes in the shortest time, it not only tests the players' observation ability, but also tests their spatial imagination. There are a lot of Rubik's Cube playing strategies on the Internet now. Most of them teach players to recover the Rubik's Cube through some specific formula. They know little about its internal mechanism. Blind formula recitation makes the Rubik's Cube a game of hand speed, thus losing its original fun. In fact, the Rubik's Cube is far less simple than it seems. The mathematics in the Rubik's Cube involves fractal geometry, linear algebra, topology, group theory, etc. Among them, group theory is the most important part to understand the solution of the Rubik's Cube.

2. Definition of group

Group theory is a mathematical concept, which aims to study an algebraic structure called group. The essence of group theory is to describe the symmetry of nature and explore the internal structural laws between various transformations [1]. Group is a set with an operation that is closed. We can describe it this way: Suppose G is a nonempty set and \( · \) is its binary operation. The result of binary operation of any two elements in G still belongs to the set, which is called group is closed. In addition, groups have many other properties [2]:

(1) Meet the associative law: if \( a, b∈G \) , then there is a unique and definite aa \( c∈G \) satisfied \( (a∙b)∙c=a∙(b∙c) \)

(2) There exists an identity element which operates with the other elements or with the other elements themselves: \( ∃e∈G \) , for \( ∀a∈G \) , satisfied \( e∙a=a∙e=a \) , where \( e \) is called an identity element.

(3) There are inverse elements, any element and its inverse operation, is equal to the identity element: \( ∀a∈G, ∃b∈G, a×b=b×a=e \) , where \( b \) is called an inverse element.

So we call G is a group for \( ∙ \) . It is important to note that elements and operations within a group are elements and operations in a broad sense. There is no rule that elements must be numbers in a real number set. Operations are not necessarily operations of addition, subtraction, multiplication and division. The corresponding elements and concepts of operations within a group can be arbitrarily specified according to our needs. Elements can be things, numbers or some combination of them. Operations can also be set operations or other more complex combinations, but we can call them a group as long as they satisfy the above rules.

A group has many classifications, which are classified according to the number of elements in the group. A group with a finite number of elements is called a finite group, and a group with an infinite number is called an infinite group. In addition, there are two-dimensional spatial rotation groups, permutation groups, Klein four-group, Symmetric Groups of Regular Polygons, and so on, categorized according to the categories and operations of the elements [3]. A permutation group is an important group in which elements in a finite group are a sequence with a fixed order, while an operation is to exchange the positions of two items in the sequence.

Subgroup is a special nonempty subset of a group. A nonempty subset H of a group G is said to be a subgroup of G if its multiplication on G also becomes a group, denoted as H ≤ G. H is a subgroup of a group G if and only if it is a nonempty set and closed under product and inverse operations. In the case that H is finite, then H is a subgroup if and only if H is closed under the operation [4].

3. Permutation group

The concept of a permutation group was briefly mentioned earlier, in which elements are sequential sequences in which elements can also be things, numbers or letters. The transformation of an ordered sequence in a permutation group into another arrangement, called a permutation [5]. Groups can also swap the positions of two items in this sequence, which is called conversion. Assuming I have a sequence \( (\begin{matrix}\begin{matrix}{x_{1}} & {x_{2}} \\ \end{matrix} & \begin{matrix}{x_{3}} & {x_{4}} \\ \end{matrix} \\ \end{matrix}) \) , I can swap two of the items to form a new sequence \( (\begin{matrix}\begin{matrix}{x_{1}} & {x_{3}} \\ \end{matrix} & \begin{matrix}{x_{2}} & {x_{4}} \\ \end{matrix} \\ \end{matrix}) \) , and by the definition of the group, this sequence should also belong to this group. Of course, I can also change other items or any two items based on the new sequence, but the result should belong to this group.

Based on the example above, I swap the position of \( {x_{2}} \) with that of \( {x_{3}} \) . We define this operation as \( (2 3) \) , similarly if \( {x_{1}} \) and \( {x_{2}} \) are swapped, it is \( (1 2) \) , and we can get a sequence \( (\begin{matrix}\begin{matrix}{x_{2}} & {x_{1}} \\ \end{matrix} & \begin{matrix}{x_{3}} & {x_{4}} \\ \end{matrix} \\ \end{matrix}) \) . If we continue with this new sequence by \( (1 3) \) , we get the original sequence \( (\begin{matrix}\begin{matrix}{x_{3}} & {x_{1}} \\ \end{matrix} & \begin{matrix}{x_{2}} & {x_{4}} \\ \end{matrix} \\ \end{matrix}) \) . Looking at this sequence, essentially the first three elements have been replaced. We define this operation as \( (1 2 3) \) , which means that elements originally above position 1 2 3 are exchanged in turn, that is, items originally at position 1 are placed at position 2, items originally at position 2 are placed at position 3, and items originally at position 3 are placed at position 1. Now that we call elements in a permutation group state, we can draw a rule from the above analysis: In a permutation group, the process of transition from one state to another, that is, permutation, can be seen as the overlap of many simple processes of conversion between two locations, thus breaking a complex process of state change into many simple small problems. We refer to the number of numbers in a substitution bracket as the order of the permutation, for example, the order of \( (1 2) \) is 2 and the order of \( (1 2 3) \) is 3. There are many properties about this type of permutation group [6]:

(1) When a state is permutated n times by n orders, it eventually returns to the state itself, for example: \( {(1 2)^{2}}=(1 2)(1 2)=1 \) , \( {(1 2 3)^{3}}=(1 2 3)(1 2 3)(1 2 3)=1 \) . That is to say, the state in the permutation group can always return to the original state after any repeated operations of a finite number of times

(2) n-order permutation processes in permutation groups can be decomposed into n-1 second-order permutation processes: \( (1 2 3)=(1 2)(1 3) \) , \( (1 2 3 4)=(1 2)(1 3)(1 4) \) , \( (1 2 ⋯ n)=(1 2)(1 3)⋯(1 n) \) .

(3) If the number of decomposed second-order permutations is odd, it is called odd permutations, and if the number is even, it is called odd permutations, for example: \( (1 2) \) is odd permutation and \( (1 2 3) \) is even permutation.

4. The Rubik’s Cube notation

Starting from 2*2*2 simplified Rubik’s Cube which contains only 8 small cubes, this simplified cube could be defined as 8 corner cubes with 3 of their faces exposed. Following the general directions: up(U), down(D), left(L), right(R), front(F), behind(B), the eight corner cubes could be named in order: up right front corner (URFC), up left front corner (ULFC), down left behind corner (DLBC) and so on. However, the most common Rubik's Cube is the third order Rubik's Cube of 3*3*3, so this paper mainly takes the third order Rubik's Cube as an example to explore the relationship between the solution of Rubik's Cube and group theory

Regarding 3*3*3 Rubik’s Cube, the corner cube number remain as 8 but the total small cube number increase to 27, with one invisible core cube in the center, while there are also 12 prism blocks with 2 faces exposed and center cubes with one faces exposed. There are respectively 6 available movement in 3 order Rubik’s Cube as each movement is cyclical movement (90° of clockwise rotation equals 270° of anticlockwise rotation). We use the following marks to indicate:

When we play Rubik's Cube, we often fix the position of the center of face, point a color of the center of face at ourselves, and fix the color of the center of face on top and bottom of the center of face, so that we can no longer rotate it. At this time, we write down all the faces of the cube as follows: top (UP), bottom (DOWN), left (LEFT), right (RIGHT), front (FRONT), back (BACK), and the corresponding operations as [7]:

(1) \( F \) : point the front face of the cube at you, then rotate it 90 degrees clockwise.

(2) \( B \) : point the back face of the cube at you, then rotate it 90 degrees clockwise.

(3) \( L \) : point the left face of the cube at you, then rotate it 90 degrees clockwise.

(4) \( R \) : point the right face of the cube at you, then rotate it 90 degrees clockwise.

(5) \( U \) : point the top face of the cube at you, then rotate it 90 degrees clockwise.

(6) \( D \) : point the bottom face of the cube at you, then rotate it 90 degrees clockwise.

In addition, for example, we use \( {F^{2}} \) to represent two \( F \) operations, and \( {F^{-1}} \) represents anti-clockwise rotation.

5. Rubik's Cube Group

We mentioned earlier that the Rubik's Cube is closely related to group theory, and explained the basic concepts of group theory, so to say, because the structure of the Rubik's Cube can explain group theory to a certain extent. We can imagine that when the cube rotates and transforms, the positions of the different color blocks in each side essentially change. If we pull them out to form a one-dimensional sequence, we call the restored states of the six faces 1. If we operate on the cube, the essence is to replace some items in this sequence. We can use n-order substitution to represent the sequence of the cubes after operation, and form a group of all possible substitution pairs [8]. We call such a group Rubik's Cube. Based on the elements and operations in the group, we can know that Rubik's Cube belongs to the permutation group in the group classification. Now let's prove that the magic cube group satisfies the definition of group and permutation group.

The number of Rubik's Cube states is obviously limited. Any transformation of the restored Rubik's Cube can always find the corresponding state in the Rubik's cube group, so the Rubik's Cube group is a finite group and closed for operations.

The unit element of the cube group is the state of the six facets restored, recorded as 1, to manipulate the cube, such as front face of the cube pointing directly at yourself and rotating 90 degrees clockwise ( \( F \) ). There is always a reverse operation of this operation( \( {F^{-1}} \) ), which restores the cube to its original state. This reverse operation is called the inverse element. For combinatorial operations, such as UUFF, its inverse element is \( {F^{-1}}{F^{-1}}{U^{-1}}{U^{-1}} \) .

It is obvious that Rubik's Cube Group belongs to a permutation group. For a combination of operations, this combination can always be carried out continuously and finally be restored to its original state. This is not unexpected. For any of the six basic operations, it can be regarded as a high-order permutation. Depending on the nature of the permutation group, the n-order permutation will be restored to its original state after repeated n times. For a combination of operations, it is nothing more than a higher-order permutation. But it always returns to its original state after repeating the total order several times.

Of course, the n-order permutations of a basic operation can also be decomposed into n-1 second-order permutations according to the characteristics of the permutation group. Similarly, the combination of several basic operations can also be decomposed into the composite of multiple second-order permutations.

6. Restrictions of Rubik's Cube

The state sequence of Rubik's Cube can't be arranged freely, just like if there is a recovered Rubik's Cube that thinks it will flip a corner of Rubik's Cube. Although we have got a new sequence, we obviously can't get this new sequence through the initial Rubik's Cube with six basic operations, that is, this state is not in Rubik's Cube group, but exists in the corresponding permutation group. That is, Rubik's Cube is actually just a subgroup of the permutation group.

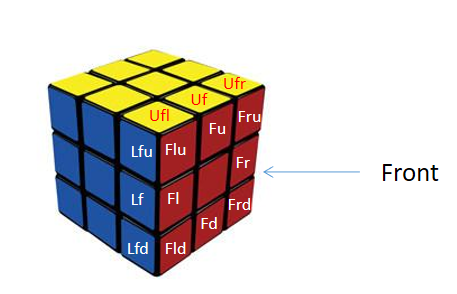
For a simple description, we numbered each face in corner and prism of the Rubik's Cube, As shown in Figure 1.

(1) Prism block: Represents two letters, the first in uppercase, indicating the direction in which the face is located, and the second in lowercase, indicating the direction adjacent to the face.

(2) Corner block: Represents three letters, the first in uppercase, indicating the direction in which the face is located, and the remained in lowercase, indicating the direction adjacent to the face.

See the figure below for details:

For a basic operation F, its corresponding replacement expression is:

\( (Lf Uf Rf Df)(Fl Fu Fr Fd)(Flu Fru Frd Fld)(Lfu Ufr Rfd Dfl)(Ufl Rfu Dfr Lfd) \)

From the above expression, this is a composite of five fourth order permutations, so this can be decomposed into a composite of 15 second order permutations. Therefore, the basic operation F is an odd permutation. The other five basic operations are all odd permutations.

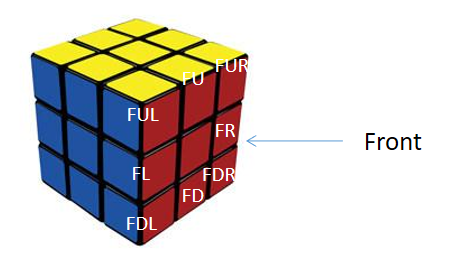
If we only consider the position permutation of the cube, we will mark the Rubik's Cube again. The edge block is represented by two capital letters, while the corner block is represented by three capital letters. As shown in Figure 2.

For a basic operation F, its corresponding replacement expression is:

\( (FL FU FR FD)(FUL FUR FDR FDL) \)

From the above expression, this is a composite of two fourth order permutations, so this can be decomposed into a composite of 6 second order permutations. Therefore, the basic operation F is an even permutation. Therefore, it is impossible to exchange any two blocks without changing the positions of other blocks through the basic operation combination of magic cube, because the exchange of the positions of any two blocks is an odd transformation, which cannot be compounded through even transformation. But we can exchange two pairs of edges or two diagonal blocks or a pair of edges and a diagonal block through basic operations [9].

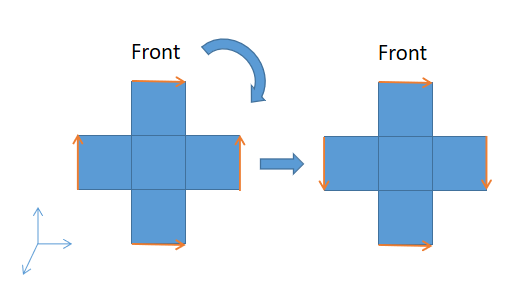
The second is obviously simpler than the first, and you can see some restrictions on the cube. However, the second does not take into account the directionality of the blocks. There can be two opposite arrangements at the same position for the prisms, and three different arrangements at the same position for the corners. With the geometric center of the cube as the origin, the right-handed spiral coordinate system is established, and the direction of the prism parallel to the coordinate axis is the positive direction of the coordinate axis. So, taking the front of the cube as an example, we do a basic operation F to observe the direction change of the prism.

As shown in Figure 3, we can see that after a basic operation F, the direction of the upper and lower prisms (FU, FD) has not changed, but the direction of the left and right prisms (FL, FR) has been flipped at the same time. The same is true for the other five basic operations, so if we only flip one prism, we will not be able to restore the cube.

Therefore, Rubik's Cube can't change freely under the basic operation, but under certain restrictions. This is why, although the number of elements in Rubik's Cube group is so large that it seems very difficult to recover, there are so many rules in it that many people are obsessed with it.

7. Homomorphism of Rubik's Cube Group

According to the previous analysis, we built a group by using generators. From this perspective, the Rubik's Cube group is not a permutation group in this sense, but a set of operations. Although the algebraic structures of the two groups are different, there is a mapping relationship between them, which we call "homomorphism".

Given group \( G \) (and calculation symbol \( * \) ) and group \( {G^{ \prime }} \) (and calculation symbol \( ⋆ \) ), if there is a function \( Γ:G→{G^{ \prime }} \) , which satisfies for any \( g,h∈G \) , has \( Γ(g)⋆Γ(h)=Γ(g*h) \) , then we call \( Γ \) a homomorphic mapping of \( G \) , or a homomorphic function.

If \( Γ \) is a surjection (that is, any element of \( {G^{ \prime }} \) is the image of an element of \( G \) ), we can conclude that the structure of \( {G^{ \prime }} \) is smaller than \( G \) , that is, simpler. Otherwise, if \( {G^{ \prime }} \) is greater than \( G \) , then it cannot shoot full shot. Therefore, in a loose mathematical language, \( {G^{ \prime }} \) has the local structure of \( G \) . This relationship must be distinguished from that of "subgroups".

We call the 8 blocks at the top of the magic cube vertex blocks, the 12 blocks on the edge of the magic cube except for the vertex blocks, and the other 6 blocks at the center of the face of the magic cube face blocks. After defining the blocks, we can understand the magic cube as a transformation group \( G \) . The elements of \( G \) are the 1-1 mapping (transformation) of the block set to itself, and the group multiplication is the composition of the 1-1 mapping (transformation composition).

8. Formula for Rubik's Cube

Depending on the nature of the Rubik's Cube group described earlier, it is possible to swap two pairs of blocks at once and change the direction of one pair of prisms for basic operations, and we also know that higher-order substitutions can be broken down into lower-order substitutions, that is, a cube can be broken down from a disrupted state to a recovered state into many basic operations so that we can actually invent our own formula for the restoration of the cube.

But when you put it into practice, it's unrealistic, it's incredibly cumbersome and the steps are lengthy. It is not easy to really invent clever and concise Rubik's Cube formula. The above mentioned is just the foundation, and mastering those is far from enough.

Through the basic permutation group, we can really get several local formulas, such as flipping edges or corner blocks, but when we apply one of the formulas, we will disturb the others. How can we exchange only one pair of edges and one diagonal block or two pairs of edges without changing the arrangement of the rest of the blocks? The answer is to use the commutator of the group. Suppose we know an operation \( P \) , its function is to turn over the prism of FU and disturb the next two layers of blocks. Then operation \( {P^{-1}} \) is to turn over the prism of FU and restore the next two layers of blocks that have been disturbed. In this way, the Rubik's Cube will be restored when \( P \) is running first and \( {P^{-1}} \) second. If we add a \( U \) operation between the two operations, and the box at the original FU position becomes FR, then \( {P^{-1}} \) will be run at this time, FR will be turned over, and the next two layers of blocks will be restored. Finally, \( {U^{-1}} \) will be run. In this way, using \( PU{P^{-1}}{U^{-1}} \) can achieve the goal of flipping FU and FR, while the other squares remain unchanged.

Perhaps it's too inefficient. With the development of computer technology, computing power has been greatly improved. Researchers are also keen on using computer programming to solve Rubik's Cube. We know that all elements of Rubik's Cube can be obtained by a combination of six basic operations, so the originator of Rubik's Cube is 6. At present, the most common way of programming to solve Rubik's Cube is to descend the group, that is, to reduce the number of possible states of Rubik's Cube by changing the origin of Rubik's Cube [10]. Although this method is amazing, it is too difficult for human understanding, so it is rarely used in Rubik's Cube games.

9. Conclusion

In this paper, we use the basic knowledge of group theory to prove that Rubik's Cube Group is a subgroup of permutation group, and prove the solvability of Rubik's Cube with its related properties. The basic idea is to decompose Rubik's Cube Group into products of simpler subgroups, and then construct the generators of each subgroup. This method has strong universality and can be directly applied to other complex cases. However, if you want to create a clever formula for Rubik's Cube, you need the help of a computer.