1. Introduction

Proteins, comprising peptide chains formed by around 20 amino acids, are fundamental macromolecules essential for various biological functions. The primary sequence of these peptide chains plays a critical role in determining protein functionality. Furthermore, the manner in which a peptide chain folds—either locally or globally—significantly influences its interactions with other chains, thereby affecting protein function. This highlights the importance of not only determining peptide sequences but also understanding their folding orders to grasp protein functionalities fully. Advanced sequencing technologies have successfully elucidated peptide sequences; however, the complex phenomenon of protein folding remains a challenging puzzle due to intricate intermolecular interactions among protein side chains [1,2].

The protein folding problem is intricately tied to the Levinthal Paradox, which illustrates the improbability of a protein sampling all possible conformations due to their vast number. This paradox highlights the spontaneous nature of protein folding, underscoring the necessity for efficient computational methods to predict protein structures [3]. The HP model, proposed by Dill, simplifies this problem by categorizing amino acids into polar and nonpolar types, focusing on their interactions within a two-dimensional or three-dimensional lattice framework. This model facilitates a clearer focus on hydrophobic and polar interactions, omitting minor chemical properties to predict energetically favorable protein conformations [4].

This paper explores the application of the Simulated Annealing (SA) algorithm in predicting protein folding, a method well-regarded for its global optimization capabilities. By implementing and evaluating an exemplary SA algorithm and comparing it to other prevalent algorithms like Genetic Algorithms (GA) and Ant Colony Optimization (ACO), this study utilizes the Hydrophobic-Polar (HP) model as a foundational framework. The efficacy of these computational predictions will be critically assessed against actual protein structures to determine the accuracy and reliability of the SA algorithm in modeling protein folding. This comparative analysis aims to validate the potential of SA and similar computational strategies in enhancing our understanding and prediction of protein structures, contributing valuable insights into the computational biology field.

2. Background

The protein folding problem aims to explain how a protein sequence of amino acids folds into a stable 3D structure. While proteins naturally fold into structures that minimize their free energy, predicting this process computationally is highly challenging. Essentially, the HP model represents proteins as self-avoiding walks on a lattice, where hydrophobic interactions drive the folding process. The HP model shows preference toward the hydrophobic effect by assigning a negative weight to interactions between adjacent, non-covalently bound H residues, imitating the preferable negatives(favorable) on the energy landscape [5]. These contacts represent the clustering of hydrophobic residues, referred to as the hydrophobic collapse, which stabilizes the protein structure.

Various optimization algorithms have been applied to this model to predict the lowest energy configuration, including Genetic Algorithms, Monte Carlo simulations, and Ant Colony Optimization. Among these, Simulated Annealing has gained attention due to its ability to escape local minima and find global energy minima, making it a competitive option for effective protein folding prediction.

3. Simulated Annealing Algorithm

3.1. Basic concept

Simulated Annealing (SA) is inspired by the physical annealing process, where materials are heated and then slowly cooled to reach a low-energy crystalline state. In the context of protein folding, SA aims to find the global energy minimum of a protein conformation by mimicking this process. The algorithm begins with a high-temperature state and allows random perturbations of the structure, where the higher energy conformations are allowed [6]. Over time, as the temperature decreases, the temperature decreases and the algorithm becomes more selective, accepting only those changes that contribute to lowering the system’s energy. Similar to the Monte Carlo simulation, SA also adopts random values or conformations in the beginning stage. However, it sufficiently limits possibilities by limiting allowed energy state progressively until the system reaches a state that most closely mimicking the global minimal energy state.

3.2. Structure of the algorithm

The SA algorithm works in several steps:

It initializes a random configuration of the protein on a lattice, which is similar to the Monte Carlo Simulation.

At each step, the structure is perturbed, allowing a change in energy (ΔE).

If the new configuration has lower energy, it is accepted. If it has higher energy, it might still be accepted with a probability proportional to the current temperature, allowing the algorithm to avoid getting stuck in local minima. This principle is referred to as the Metropolis Criterion.

As the algorithm progresses, the temperature is gradually decreased, reducing the likelihood of accepting higher energy states, which encourages convergence toward the global minimum.

3.3. Example code

An example of Simulated Annealing applied to protein folding can be found on GitHub, where a Python implementation using the HP model is provided. This code on GitHub, provides a practical application and optimization of SA algorithm with the HP model effectively demonstrates the methodology in the algorithm, enabling an evaluation of the algorithm’s functionality in comparison to other algorithms [7]. To test for the efficacy of the code, three example runs were made with insulin, hemoglobin β-subunit, and lysozyme c.

The example SA algorithm for protein folding starts by mapping the amino acids of a protein onto a grid using the Hydrophobic-Polar (HP) model. These placements significantly impact the overall stability of the protein due to the interactions between adjacent non-polar residues, which the energy function evaluates.

The structure of the Simulated Annealing (SA) algorithm as used in the protein folding code follows a systematic approach grounded in global optimization principles, particularly the Metropolis Criterion [8]. This criterion enables the algorithm to probabilistically accept higher-energy configurations, which is vital in escaping local minima and progressing toward the global energy minimum.

At the heart of the algorithm is a perturbation mechanism that randomly adjusts the configuration of the protein on the lattice. These adjustments allow the algorithm to explore different conformations and calculate the resulting energy change (ΔE) in that conformation. If the perturbation leads to a lower energy state, the new configuration is accepted outright. However, even if the perturbation results in a higher energy state, it may still be accepted based on the Metropolis Criterion, which relies on a probability proportional to the current temperature. This probability is calculated using the formula: P=exp(-ΔE/T) where ΔE is the energy change, and T is the temperature. This probabilistic acceptance ensures that the algorithm does not get trapped in suboptimal solutions, a common challenge in other optimization techniques like Genetic Algorithms (GA) and Ant Colony Optimization (ACO), which may prematurely settle on local minima without this flexibility.

As the algorithm progresses, the temperature is gradually reduced according to a predefined cooling schedule. The cooling schedule is vital for controlling how quickly the algorithm transitions from exploring a wide range of possible configurations to refining the best configuration found. If the cooling occurs too rapidly, the algorithm is prone to freezing in a high-energy, suboptimal state. Conversely, too slow a cooling process can lead to unnecessary exploration and extended runtimes, increasing the duration of the algorithm run time.

It is observed that the SA algorithm’s strength lies in its ability to strike a balance between exploration and exploitation. Early on, the algorithm explores a broad range of configurations, accepting higher-energy states to avoid local minima. As the temperature decreases, the focus shifts toward fine-tuning the best configurations, making it more likely to find the global minimum energy state. This ability to escape local minima is where SA outperforms other algorithms like GA, which may prematurely converge to suboptimal solutions due to a lack of such probabilistic flexibility. Moreover, the algorithm’s performance is highly sensitive to parameters like the initial temperature and cooling schedule. A well-optimized cooling schedule allows SA to effectively navigate the complex energy landscape of protein folding, leading to a lower-energy and more accurate protein structure. In contrast, GAs and ACOs, while effective in exploring the solution space, often require more intricate parameter tuning and tend to be more prone to getting stuck in local minima, especially in problems with complex energy landscapes.

3.4. Analysis of output

The effectiveness of the SA algorithm is typically evaluated by comparing the predicted structure’s energy to the known native structure. The Root Mean Square Deviation (RMSD) is often used to quantify the accuracy of the predicted fold. In the example code adopted, however, RMSD is not available since the model relies on a 2D lattice model. Instead, the 2D predicted output is viewed as a superimposition to the other 3D prediction using AlphaFold, a 3D machine learning prediction model for protein folding. The respective predicted structure of insulin, hemoglobin β-subunit, and lysozyme c is shown below. As show in the figure 1 to the figure 3.

Insulin:

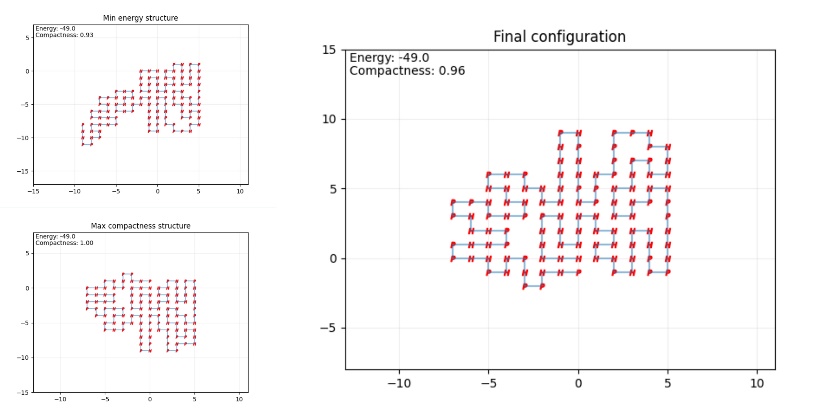
Figure 1. Final configuration (Photo credit: Original).

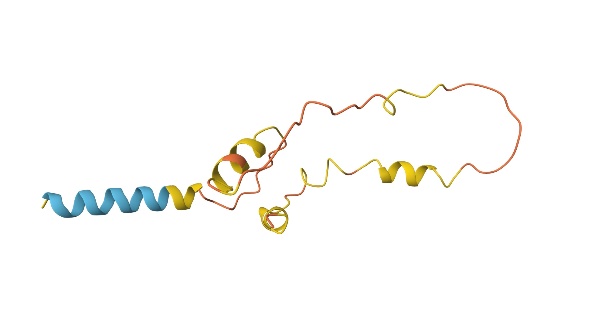
Figure 2. Predicted 3D Protein Folded Structure using AlphaFold (Photo credit: Original).

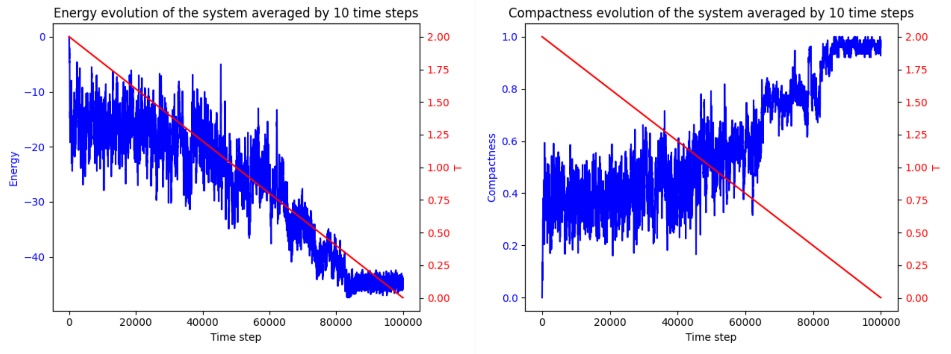
Figure 3. Predicted Structure and Energy Evolution Trajectory using SA (Photo credit: Original).

In the prediction for hemoglobin, due to he limitation in 2D lattice model, the final configuration varied distinctly form the 3D AlphaFold projection. Nevertheless, the minimal energy structure predicted, resembles the superimposition of the 3D prediction onto a 3D planar model, which partly manifests the effectiveness of the SA algorithm. As show in the figure 4 to the figure 6.

Hemoglobin β-subunit:

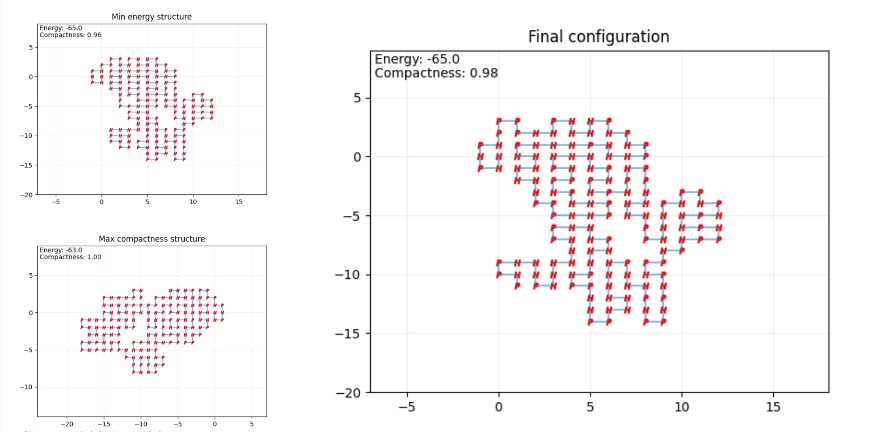
Figure 4. Final configuration (Photo credit: Original).

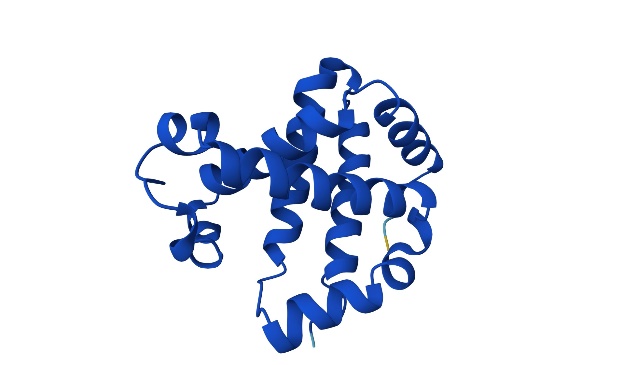
Figure 5. Predicted 3D Protein Folded Structure using AlphaFold (Photo credit: Original).

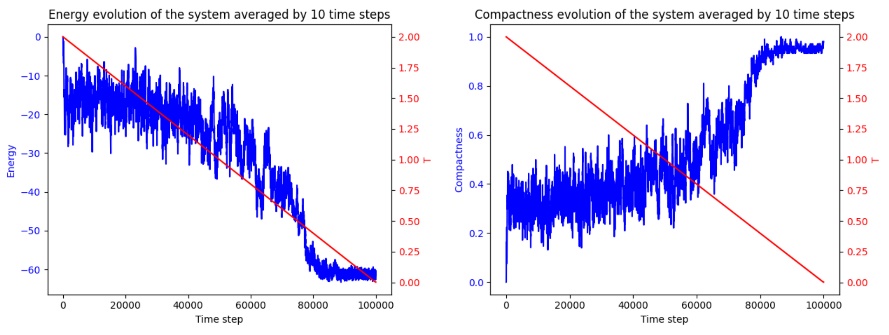
Figure 6. Predicted Structure and Energy Evolution Trajectory using SA (Photo credit: Original).

Similar to the insulin prediction, the 3D AlphaFold prediction resembles closely to the 2D SA algorithm prediction. Both structures exhibit a circular structure and similar arrangements. Notably, the max compactness, max energy, and the final configuration in the SA prediction are almost identical rotamers of one another. As show in the figure 7 to the figure 8.

Lysozyme C:

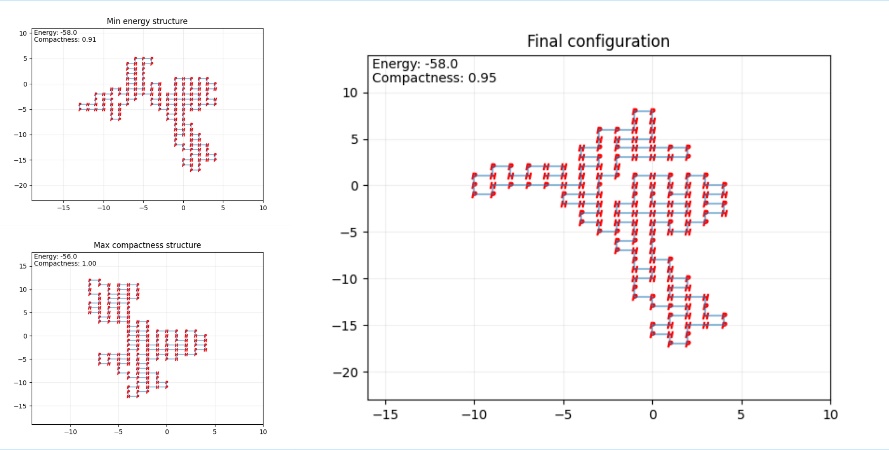
Figure 7. Final configuration (Photo credit: Original).

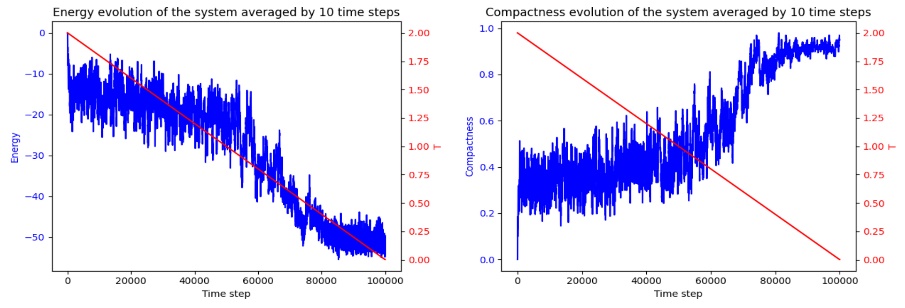
Figure 8. Predicted 3D Protein Folded Structure using AlphaFold (Photo credit: Original).

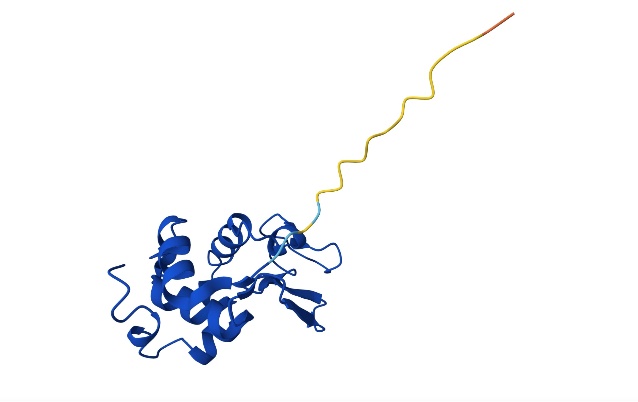
Figure 9. Predicted Structure and Energy Evolution Trajectory using SA (Photo credit: Original).

For the case of lysozyme C, the SA prediction varies a lot from the AlphaFold prediction. Due to the complexity of the sequence, the 3D SA prediction does not seem to be resembling the superimposition of 3D prediction. Because the 2D lattice model is heavily simplified, the 3D predication is likely more realistic to resemble how the protein folds in vivo. In terms of compactness optimization, SA focuses on creating a compact hydrophobic core, but in 2D, this is much less defined and can’t reflect the true spatial arrangement. AlphaFold, on the other hand, shows a more accurate folding pattern that hides hydrophobic residues inside and allows for the creation of the protein’s active site.

4. Comparison with Other Algorithms

Genetic Algorithm (GA). Genetic Algorithms (GAs) mimic the process of natural selection to optimize protein folding. They use crossover and mutation operators to explore the protein’s conformational space. GAs can be effective, particularly when it comes to generating diverse solutions, but they are prone to premature convergence, where the algorithm settles on a suboptimal solution too early. Through iterations, GA uses mutation and genetic progression that result in the best fitness for the condition [9]. In contrast, Simulated Annealing’s probabilistic acceptance of worse solutions allows it to avoid this pitfall. While GAs can achieve low RMSD values, SA generally excels in escaping local minima and achieving lower energy folds when parameters like the cooling schedule are appropriately tuned [10]. By contrast, GA may be more prone to be stuck in local minimum rather than than the global minimum. Notably, in one study, Chen et al. employed a SA/GA hybrid algorithm in wide and antenna matching network optimization that results in the least error using a less iteration number than either algorithm alone [11]. This may potentially document an enhanced algorithm performance with hybrid models.

Ant Colony Optimization (ACO). Ant Colony Optimization (ACO) is another algorithm used for protein folding prediction. ACO simulates the behavior of ants searching for food, where artificial “ants” deposit pheromones to guide others toward better solutions. While ACO can effectively explore the solution space, it is susceptible to getting trapped in local minima, leading to less accurate predictions and higher RMSD values compared to SA. ACO’s success largely depends on the proper tuning of pheromone-related parameters, and it often requires more iterations to match the accuracy of SA. Studies have shown that SA achieves lower RMSD values and higher accuracy in predicting protein structures than ACO [12]. On the other hand, SA has been shown to result in accurate of protein structures less than 3Å from the native structure [13].

Superiority of the Simulated Annealing Algorithm. As a stochastic optimization technique, Simulated Annealing offers several advantages over other algorithms in the context of protein folding prediction. Its ability to probabilistically accept worse solutions during the early stages of the process allows it to explore a broader range of conformations, helping it avoid local minima. Furthermore, SA’s gradual reduction in temperature helps fine-tune the structure as the algorithm progresses, leading to lower energy states. In comparison to GAs and ACO, SA generally provides more accurate predictions with fewer iterations, particularly when dealing with complex energy landscapes. However, the performance of SA heavily depends on its cooling schedule and other parameters, which must be carefully optimized for each specific problem.

The Metropolis Criterion in SA plays a significant role in this by enabling the acceptance of higher energy configurations during early iterations, increasing the likelihood of escaping local energy minima and eventually discovering the global minimum. This ability is critical in protein folding, where the energy landscape is vast and filled with numerous local minima. As the energy evolution chart may reveal, these local mimimas have low energy values that are similar to the eventual prediction. Hence, the algorithm is susceptible to be trapped if not properly tuned. This makes SA more adaptable and efficient compared to GAs and ACO, which often require complex parameter tuning and extensive iterations to achieve comparable results

Discussion of Future Development Directions. Looking forward, the use of hybrid models that combine Simulated Annealing with other algorithms, such as GAs or more sophisticated machine learning models, offers exciting prospects for protein folding prediction. One potential development involves dynamic cooling schedules in SA, where the rate of cooling is adapted based on the progress of the solution search. This approach could improve the efficiency of SA, particularly in large protein structures where static cooling schedules might lead to suboptimal solutions. Additionally, refining SA by integrating it with molecular dynamics simulations could potentially provide more accurate representations of protein folding, as it would allow the algorithm to account for the continuous movements and interactions between amino acids. In the current phase, most prediction tools or models tend to only simulate the static structure of folded protein by itself. On an intermolecular spectrum, however, the protein is also influenced by other cofactors or global catalytic components in its native environment that may further alter its folding mechanism and thereby, altering its functionality. With this being said, if one can take these components into account for the prediction of protein, a better understanding of proteins on a molecular and global perspective can be achieved.

Nowadays, a particularly promising avenue is the integration of SA with machine learning models like AlphaFold, which uses deep learning techniques to predict protein structures with unprecedented accuracy. AlphaFold leverages large datasets of protein sequences and their corresponding structures to learn patterns in protein folding that can generalize to new proteins. Unlike SA, which directly optimizes for energy states using a heuristic approach, AlphaFold predicts structures by modeling the evolutionary and physical constraints of proteins, after learning the existential protein structures and folding mechanisms. AlphaFold uses neural networks to generate predictions of protein folding, achieving remarkable results with a Global Distance Test (GDT) score of over 90. This is a significantly different approach compared to the HP model and SA, which focus on hydrophobic and polar interactions and energy minimization as key factors driving folding.

One key limitation of AlphaFold, however, is that it often works best for proteins with extensive evolutionary information in its training set. SA, in contrast, does not rely on such data and can be applied to any protein sequence using physical principles. Due to this difference, if there is a new mutated protein that shows no evolutionary record in the library, AlphaFold may be less effective in predicting its folding. As such, a hybrid model that integrates the data-driven predictions of AlphaFold with the physical optimization techniques of SA could offer even greater accuracy and flexibility in predicting protein structures, particularly for novel or poorly understood proteins.

Future Research and Applications. As protein structure prediction tools evolve, there is a growing demand for more dynamic and integrated approaches that combine the strengths of multiple algorithms. The fusion of Simulated Annealing with machine learning models like AlphaFold could lead to powerful new tools capable of handling both the physical principles underlying protein folding and the wealth of data from evolutionary biology. Additionally, improvements in cooling schedules and the ability to fine-tune parameters dynamically could make SA even more competitive. Another promising direction is the inclusion of ligands, ions, and post-translational modifications in prediction models, which may provide a more accurate predictions of protein functionality and interactions in its native environment.

The broader integration of SA with drug discovery applications has already revolutionized the pharmaceutical industry by enabling faster and more accurate predictions of protein-drug interactions. By refining the folding predictions of proteins that serve as drug targets, SA-enhanced models could accelerate the design of drugs with higher specificity and efficacy.

5. Conclusion

This study has critically assessed the application of the Simulated Annealing (SA) algorithm within the framework of the HP model for protein folding prediction. The analysis underscores SA's ability to effectively navigate global optimization challenges, distinguishing itself from other algorithms like Genetic Algorithms and Ant Colony Optimization due to its robust capability in escaping local minima. While the HP model's simplification into merely polar and nonpolar amino acids omits complex interactive properties, the SA algorithm still achieves a commendable level of accuracy in predicting protein structures with a low RMSD value. However, limitations arise when comparing 2D SA predictions with the more intricate 3D structures generated by AlphaFold, particularly for complex proteins where SA may not accurately replicate detailed folding patterns such as the hydrophobic core and active site positioning.

Future Research Directions: Considering the effectiveness of SA for simpler protein sequences and the superior predictive accuracy of machine learning models like AlphaFold, future research should explore the development of hybrid models. These models would ideally integrate the strengths of SA's optimization capabilities with the advanced learning algorithms of models like AlphaFold. This hybrid approach could potentially enhance predictive accuracy, especially for novel or complex protein structures that neither traditional algorithms nor current machine learning models can accurately predict alone. The potential for such hybrid models to revolutionize protein folding prediction is immense, opening up new possibilities in fields ranging from molecular biology to therapeutic development. Continued advancements in integrating computational methods with machine learning are expected to push the boundaries of protein research, leading to breakthroughs in understanding biological processes and accelerating innovations in drug discovery..