1. Introduction

As mentioned earlier, research directed at the Carnot cycle has been ongoing. It is well known that, ideally, the Carnot cycle is the most efficient. This also means that the research on the Carnot heat engine aimed to make the working environment of the heat engine for practical applications closer to the ideal environment, so as to achieve the highest thermodynamic efficiency in theory. This paper aims to explain the Carnot cycle and list the factors that affect its efficiency. This will give direction on how to improve its efficiency. The paper will discuss how the Carnot cycle was developed, what it is, why it is the most efficient, what factors affect the actual efficiency of the Carnot cycle, and what directions are most likely to be realized to improve the existing Carnot heat engine. Improvements to the Carnot heat engine can have a significant impact because it is used almost everywhere in our practice, including automobiles, air conditioners, and many more heat engines. Undoubtedly, improvements to Kano heaters can improve resource efficiency, reduce energy waste, ease resource constraints, minimize emissions and promote sustainable development.

2. The first law of thermodynamics and the Carnot cycle

2.1. The development of the Carnot cycle

The invention of the steam engine is the first widespread use of heat engines since the Industrial Revolution in the eighteenth century. It has contributed significantly to the industrial revolution and the development of human productivity. But until the early nineteenth century, the efficiency of the steam engine was still only 3 to 5 percent[1]. The scientists and engineers of the time pinned their hopes on structural improvements to the steam engine to reduce heat loss and gas loss, and even friction loss of effective work. There was no mistake in this direction in general. However, due to the limitations of the scientific equipment and theoretical foundations of the time, little was achieved. So, people turned to the theory of heat engines, hoping to fundamentally improve the efficiency of heat engines. This theory is the French scientist Carnot’s proposed Carnot cycle.

2.2. The Carnot cycle

The Carnot cycle is a reversible cycle consisting of two isothermal processes, two adiabatic processes.

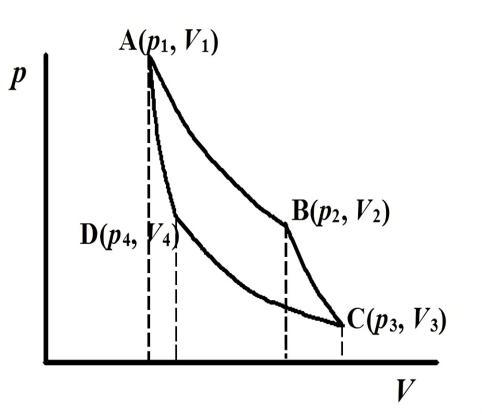
Figure 1: Carnot cycle diagram.

The Carnot cycle consists of four steps: A~B, isothermal heat absorption, in which the system absorbs heat from a high-temperature heat source; B~C, adiabatic expansion, in which the system performs work on the environment and the temperature decreases; C~D, isothermal exothermic, in which the system emits heat to the environment and the volume is compressed; D~A, adiabatic compression, in which the system recovers from its original state, and the system performs negative work on the environment in the isothermal compression and adiabatic compression processes. In the process of isothermal and adiabatic compression, the system performs negative work on the environment. In figure 1, the Carnot cycle is set up in an ideal state. The two heat sources, T1 and T2, are ideal heat sources, and their temperatures do not increase or decrease as the cycle progresses, but always remain at a constant temperature, which means that they absorb and release heat at a constant rate. In reality, the curve of the Carnot cycle is not so smooth.

3. The Carnot cycle is the most efficient.

3.1. The Carnot cycle is the most efficient

For the Carnot cycle, the highest efficiency is reflected in the fact that it is a reversible cycle. What is the difference between a reversible Carnot cycle and an irreversible Carnot cycle? Why is a reversible Carnot cycle more efficient than an irreversible Carnot cycle? For a reversible Carnot loop, we can express its efficiency as :W =Q 1-Q 2, η= W/ Q 1 . For an irreversible Carnot loop, we can express its efficiency as: W '=Q 1-Q 2-Q 3 , η'= W '/ Q 1 . [2] For a reversible Carnot cycle, the net work done by the circulatory system on the outside is equal to the heat absorbed, Q 1, minus the heat released, Q 2, since there are no dissipative factors such as friction, incomplete heat sources, and incomplete insulation. With these loss factors removed, the reversible Carnot cycle is undoubtedly more efficient.

What about a Carnot cycle versus a non-Carnot cycle? Assuming that in the cycle under consideration, the total sum of heat absorbed by the work mass from the outside world is Q1, the total sum of heat released to the outside world is Q2, and the net work done to the outside world is A, the efficiency of this arbitrary cycle is: η = A ' /Q1 ' = Q ' 1-Q ' 2/ Q ' 1 =1- Q ' 2/ Q ' 1 .,where A is the net work done by the work mass to the outside world in a corresponding Carnot cycle. And we get: Q1 >A>0,Q2 ' >Q2 >0,Q1 ＇ >0, α>0 [3]. Therefore, after mathematical derivation, we find that the efficiency of a Carnot cycle is always greater than any other cycle, and the two are equal only if the other cycle is also a Carnot cycle.

3.2. The factors that affect the actual efficiency of the Carnot cycle

As mentioned earlier, the reversible Carnot cycle is built in an ideal state. It consists of three conditions: complete insulation, no influence of friction, and an ideal gas. Thus, the factors affecting the efficiency of the Carnot cycle are the ones that distinguish the ideal state from the actual state. Moreover, as the paper that mentioned at the beginning, in the eighteenth century, in order to improve the efficiency of the steam engine, the scientists of the time considered aspects. After years of development, our basic science has come a long way again, and if we want to improve the efficiency of the Carnot cycle, it is a good direction to start with these three factors.

4. Improvements to existing Carnot heaters

A Carnot heat engine is a dual heat engine consisting of a high temperature and a low temperature heat source. Therefore, optimization for the dual heat source heat engine model is also feasible. Most of the improvements for Carnot heat engines consider the irreversible rate of the machine's internal-work mass cycle. However, there are also papers that ingeniously consider the irreversibility inside the machine[4]. It also demonstrated that the irreversibility inside the machine significantly affects the efficiency of the Carnot heat engine. This is undoubtedly a good research direction. Because as we mentioned before, the efficiency of Carnot reversible heat machine is greater than the efficiency of Carnot irreversible heat machine. For much of the past, more scholars have aimed to increase the power and efficiency of Carnot heat engines [5-10].

And in recent years, people through the exploration of the quantum field intends to improve the efficiency of quantum Carnot heat engine by reducing the ineffective work such as loss of heat leakage coefficient and other aspects of the Carnot heat engine from the point of view of quantum mechanics. This thesis obtains expressions for the performance parameters of the cycle, such as power [11], efficiency and effective power, by the method of modeling a quantum Carnot heat engine cycle with two fermions in a generalized potential well as the working matter and investigates the effects of the heat-leakage coefficient and the ratio of the width of the potential well on the performance of the cycle. It is creatively proposed that the heat leakage coefficient has no effect on the power under the same potential well conditions, while the efficiency and effective power decrease with the increase of the heat leakage coefficient.

When effective power is used as the optimization objective, it reflects a trade-off between power and efficiency, which means that the heat engine will sacrifice some of the power to obtain higher efficiency. Moreover, the following year, the paper presented a thermodynamic optimization of a quantum Carnot heat engine in the presence of extreme relativistic particles. Again, modeling the quantum Carnot heat engine cycle based on extreme relativistic particles in a one-dimensional infinite deep potential well. Expressions for the performance parameters such as power, efficiency and effective power of the cycle are derived. Further, it also investigates the effects of parameters such as the heat leakage coefficient on the performance of the cycle. The results show that the heat leakage coefficient has a large effect on the efficiency, and one factor that has a large effect on the dimensionless power and effective power is the temperature ratio of the working matter. A more important major factor is the probability that the particle is in the first excited state energy level, which significantly effects on power and efficiency. This undoubtedly drives the optimization of the efficiency of Carnot heat engines in the quantum domain and further shows that the direction of optimization in quantum Carnot heat engines is feasible. In fact, research on quantum Carnot cycles and quantum Carnot heat engines has been in our sights since 2006. It [13] analogized the potential well wall of the infinitely deep potential well and the piston wall of the classical Carnot cycle, and likewise specifically compared the similarities and differences of the process equations for the isothermal and adiabatic processes of the classical Carnot heat engine, the nonrelativistic quantum Carnot heat engine, and the extreme relativistic quantum Carnot heat engine. In this way, it is concluded that the efficiency equation in the quantum Carnot cycle is similar to the efficiency equation in the classical Carnot cycle. As far as we know, the reversible Carnot cycle is almost unrealizable under the conditions of classical mechanics. However, under quantum conditions, the possibility of a reversible quantum Carnot cycle does exist.

Figure 2: Schematic diagram of thermal motion.

5. Conclusion

From the earliest steam engine to the later internal combustion engine, the development of the Carnot heat engine has played a vital role in the industrial history of mankind. The optimization of the Carnot heat engine has been the focus of many scientists and engineers. It is not only about efficiency, but improving the efficiency of the Carnot heat engine can contribute to the discovery and expansion of the field of thermodynamics. In the future, a more efficient Carnot heat engine can help to effectively reduce resource waste and environmental pollution and realize sustainable development. The purpose of this paper is to summarize the past development direction and future development direction of Carnot heat engine, which is quantum Carnot heat engine. Restricted by material limitations, it has become more and more difficult to reduce losses and increase the efficiency of Carnot heat engines from the perspective of thermal insulation, and it is even more difficult to start with the means of converting the Carnot cycle workmass into an ideal gas. The quantum Carnot heat engine fundamentally changes the situation of the irreversible Carnot cycle under classical mechanical conditions, opening up a whole new field for the optimization of the Carnot heat engine.