Advanced Scattering Analysis of Targets under Plane Waves  and Electromagnetic Vortex Waves for Stealth Applications

Chuanxiang Xu

doi:10.54254/2753-8818/2025.19950

1. Introduction

Radar Cross Section (RCS) is a key concept in radar detection and stealth technology, representing the reflective cross-sectional area used to measure the radar signature of a target [1, 2]. Radar systems operate by transmitting electromagnetic waves that interact with an object and then receiving the reflected signals [3]. The strength of the reflected signal determines the target's detectability: the smaller the RCS, the less visible the target is on the radar. Typically, one of the goals of radar stealth technology is to minimize the RCS of objects to make them harder to detect.

In recent years, researchers have explored new waveforms carrying Orbital Angular Momentum (OAM), such as electromagnetic vortex waves, as an alternative to traditional plane waves [4, 5]. OAM waves possess a unique helical phase structure, enabling them to carry additional information, which in turn generates new effects in the scattering characteristics of targets. Compared to traditional plane waves, OAM waves exhibit more complex scattering behaviors when interacting with target objects, and their helical phase characteristics help control and optimize scattering directionality and power distribution [6, 7]. Existing studies have shown that OAM waves modify the phase interference pattern between electromagnetic waves and the target, thereby affecting the target's RCS [8]. Specifically, this paper presents a detailed comparison of the RCS characteristics of targets under plane wave and OAM-based vortex wave excitation [9]. The results demonstrate that OAM waves can significantly reduce RCS under certain conditions, making targets more challenging to detect by radar. This is particularly important for enhancing target stealth capabilities in modern warfare, where increasing detection techniques make stealth and countermeasures increasingly challenging [10].

Furthermore, the unique phase characteristics of OAM waves can be used to achieve selective detection of different targets, offering more flexibility for radar systems. For instance, different OAM modes (determined by the topological charge $ ll $ ) can be used to distinguish multiple targets, enabling the system to achieve better target identification and classification in complex electromagnetic environments [11, 12]. Therefore, OAM waves have substantial potential applications in radar stealth and electronic countermeasures. In practical applications, OAM waves can be combined with existing Multiple Input Multiple Output (MIMO) technology and phased array techniques to further enhance radar detection capability and flexibility [13]. For example, MIMO-OAM integration can provide additional information transmission dimensions based on spatial multiplexing, greatly improving system performance. Moreover, the helicity of OAM waves and their distribution characteristics in the scattering field can be combined with adaptive beamforming techniques to optimize energy distribution in the target region, enhancing radar system effectiveness [14].

The applications of OAM waves are not limited to communication but also extend to radar sensing, imaging, and rotational Doppler detection. In radar sensing, the phase structure of OAM waves provides an additional information dimension, enhancing the detection and identification of complex targets [15]. Using OAM modal characteristics, radar systems can differentiate and selectively detect multiple targets, significantly improving system flexibility and robustness. In the field of imaging, OAM waves have significant applications, especially in optical and radar imaging. Due to the orbital angular momentum carried by OAM waves, their helical phase fronts can enhance image contrast and resolution. In certain rotationally symmetric target imaging scenarios, OAM waves exhibit superior imaging performance compared to traditional plane waves [16, 17]. Additionally, the unique properties of OAM waves show great potential in novel imaging methods such as quantum imaging and correlation imaging, providing a new pathway for high-resolution imaging. Rotational Doppler detection is another important application area for OAM waves. When OAM waves illuminate a rotating target, the target's rotation induces frequency shifts in the echo signal, known as the rotational Doppler effect [18]. By analyzing these frequency shifts, the rotational speed and direction of the target can be precisely measured. Compared to traditional Doppler radar, OAM waves provide more information when detecting rotational motion, particularly in applications such as machinery monitoring and astronomical observation, offering new means for accurate measurement of rotational movements [19].

In summary, OAM waves exhibit broad application prospects in communication, radar sensing, imaging, and rotational Doppler detection. Their unique phase structure and orbital angular momentum characteristics bring new ideas to various applications, especially in scenarios requiring high resolution, multi-target discrimination, and rotational motion detection [20].

2. Definitions of RCS and ORCS

RCS represents the echo intensity produced by a target for incident radar waves, defined as [21]:

$ σ=\underset{R→∞}{lim}4π{R^{2}}\frac{|{E_{s}}{|^{2}}}{|{E_{i}}{|^{2}}} $ (1)

where $ {E_{s}} $ represents the scattered field, and $ {E_{i}} $ represents the incident field. This relationship mainly applies to far-field conditions, where the distance $ R $ tends to infinity, allowing an assumption of plane wave incidence. RCS is an important characteristic of a target, influencing the reflected signal strength and detection range of radar [22, 23].

This paper also examines the radar cross section based on orbital angular momentum (ORCS), which is an RCS modification for OAM waves. The distinctive feature of OAM waves is their helical phase front, and the existence of orbital angular momentum changes the interaction between electromagnetic waves and the target.

Under plane wave illumination, the RCS of a target mainly depends on its geometric characteristics, material properties, and incident angle [24]. The electromagnetic field of plane waves is uniform and linear; when interacting with a target, the induced current on the target surface macroscopically aligns with the incident wave in both phase and frequency, allowing traditional physical optics approximation methods to describe the scattering characteristics. In this scenario, the RCS is determined by the coherent superposition of the reflected electromagnetic wave and the incident wave, with the directionality and intensity of reflection closely related to the target's shape and material.

In contrast, due to the helical phase structure of OAM waves, more complex scattering behavior emerges during their interaction with the target. The helical phase front of OAM waves means that their electromagnetic field exhibits rotational symmetry during propagation, distinct from that of plane waves. When OAM waves incident on a target, the induced current density on the target surface is influenced not only by the incident magnetic field but also by the helical phase of the OAM wave. This leads to a more complex distribution of induced current on the target surface, affecting both the phase and amplitude of the scattered field [25].

These unique phase effects create new scattering characteristics, especially in the distribution and directionality of scattered power. Specifically, the presence of orbital angular momentum introduces an additional phase factor to the scattered signal, leading to a more complex spatial distribution of the scattered signal, with increased diversity in scattering directions and partial energy dispersal across multiple directions [26]. This often results in a reduced RCS in certain directions, decreasing the radar detectability of the target, which is highly significant for stealth applications.

By using the physical optics approximation, the impact of OAM waves on RCS characteristics can be evaluated, especially under conditions where OAM radar interacts with targets. These modifications allow ORCS to describe the scattering characteristics of targets under OAM wave incidence more accurately, compared to the traditional RCS, which reflects the more complex features of targets excited by multimodal waves. Therefore, OAM waves show unique advantages in stealth technology and multi-target identification.

3. Scattering from a Flat Plate Under Plane and Vortex Waves

This study explores the scattering phenomena of a metallic flat plate target under electromagnetic vortex waves. The metallic flat plate is a typical simple target whose scattering characteristics are easily analyzed and modeled under electromagnetic wave irradiation. Based on the physical optics approximation, the induced current density on the target surface is estimated from the instantaneous value of the incident magnetic field, and the scattered field is calculated by integrating these induced current densities. The physical optics approximation is an effective method for handling large target scattering problems, especially suitable when the incident wavelength is much smaller than the target size [27].

For plane waves, the RCS can be represented by the simplified equation [28]:

$ {σ_{plane}}=f(θ,ϕ,geometric characteristics) $ (2)

Assuming linearly polarized incident waves, polarization effects are neglected in this study. Linear polarization simplifies the model, allowing us to focus more directly on the impact of other wave properties (such as orbital angular momentum) on scattering characteristics.

For OAM waves, the electric and magnetic fields can be expressed as:

$ {E_{OAM}}={E_{0}}\cdot {e^{ilϕ}}\cdot f(r,θ) $ (3)

where $ l $ represents the topological charge or OAM mode, characterizing the helical nature of the beam. This phase dependence of OAM waves results in scattering behavior distinct from that of traditional plane waves, particularly in scattering directionality and power distribution. Using physical optics methods, the induced current density on the target can be approximated as proportional to the instantaneous value of the incident magnetic field, greatly simplifying the calculation process while ensuring sufficient accuracy [29].

4. Physical Optics Approximation Method

This section describes the physical optics approximation method, which is applicable to electrically large targets and high-frequency electromagnetic waves. The physical optics approximation assumes that the induced current on the target is directly related to the incident field, providing high computational efficiency for solving electromagnetic scattering problems. The steps are as follows:

4.1. Calculation of Incident Field

The incident field on the target is represented as:

$ {E_{inc}}={E_{0}}\cdot {e^{i(ωt-kr)}} $ (4)

This equation represents the propagation of electromagnetic waves in space, where $ ω $ is the angular frequency, $ k $ is the wavenumber, and $ r $ is the propagation distance. For OAM waves, the helical structure of the phase front results in a more complex spatial distribution of the electric field, distinguishing it significantly from ordinary plane wave propagation characteristics.

Assuming the induced current is proportional to the incident field, for a flat plate lying in a plane with normal vector $ \hat{n} $ :

$ {J_{ind}}=\hat{n}×{H_{inc}} $ (5)

The magnitude and direction of the induced current are determined by the incident magnetic field, with these currents re-radiating from the target surface to form the scattered field. For electrically large targets, the induced currents are closely related to the electromagnetic characteristics of the target as a whole.

The backscattered field vector from a flat plate target is obtained using the Stratton-Chu equation and the physical optics approximation:

$ {E_{scattered}}=\oint _{S}[(∇×H)-iωϵE]\cdot {e^{ikr}}dS $ (6)

where the integral is performed over the target surface, and $ ϵ $ represents the dielectric constant. The Stratton-Chu equation is a classical method for solving the scattered field from a known current distribution. By applying the physical optics approximation, these equations can be greatly simplified, allowing efficient calculation of scattering characteristics.

Neglecting absorption effects, the total reflected energy must equal the total incident energy:

$ {P_{reflected}}={P_{incident}} $ (7)

Energy conservation is a fundamental principle in electromagnetic scattering, ensuring that no energy is lost during the scattering process.

4.2. Analytical Expression of ORCS

The analytical expression for the ORCS of a flat plate target is given by:

$ {σ_{OAM}}={A_{⊥}}\cdot (1+\frac{{l^{2}}}{{k^{2}}}) $ (8)

where $ l $ represents the topological charge of the OAM, and $ k $ is the wavenumber. Compared to the traditional RCS, ORCS introduces a correction related to the orbital angular momentum, making scattering characteristics more complex and diverse. $ {A_{⊥}} $ represents the orthogonal projection area of the flat plate relative to the line of sight (LOS).

More specifically, the topological charge $ l $ determines the helical phase structure of the OAM wave, affecting the interaction between electromagnetic waves and the target surface. As $ l $ increases, the helicity of the incident wave strengthens, resulting in a more complex distribution of induced current density on the target surface. This complexity manifests in both the phase and amplitude of the induced currents, causing greater diversity in the spatial distribution of the scattered field.

This phenomenon has significant implications for stealth technology, as scattering power concentration typically makes a target more detectable, while dispersing the scattering reduces the radar's ability to obtain a sufficiently strong echo signal to determine the target's position and features. Therefore, by controlling the topological charge of the OAM wave, the RCS of a target can be effectively adjusted, particularly in tactical stealth applications where appropriate values of $l$ can be selected for optimal stealth performance. Consequently, ORCS exhibits better stealth performance under certain conditions compared to traditional RCS, providing more options and flexibility in complex electromagnetic environments.

5. Results

5.1. Peak Power Variation (Main Lobe)

For OAM waves, the peak power distribution depends on the value of the topological charge $ l $ . For smaller values of $ l $ , the beam is more concentrated, forming a power peak at $ θ=0 $ . As $ l $ increases, the complexity of the OAM wave causes signal dispersion, with the peak slightly reduced and reflected power more evenly distributed. The dispersion of power implies that the reflected signal is uniformly distributed in space, thereby reducing the target's detectability in certain directions, which is crucial for stealth.

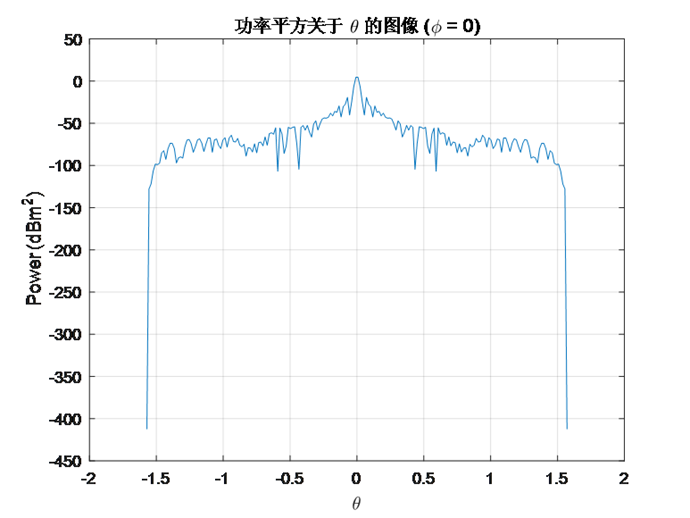
/word/media/image1.png

Figure 1: Power square diagram vs. $ θ $ (plane wave)

/word/media/image2.png

Figure 2: Power square diagram vs. $ θ $ (OAM)

This variation in peak power significantly affects the RCS of the target. Smaller values of $l$ lead to concentrated scattering energy in specific directions, particularly in the main lobe direction, indicating larger RCS in those directions, making the target more easily detected by radar. However, as $ l $ increases, the phase complexity of the OAM wave results in more uniform distribution of scattering energy across multiple directions, thereby reducing the RCS in any particular direction. This can achieve an RCS "diversity" effect, reducing the probability of obtaining a strong return signal at specific radar observation angles.

The RCS diversity effect is significant for stealth technology. By adjusting the topological charge of the OAM wave, the target's scattering characteristics can be effectively controlled, reducing its detectability at specific radar observation angles. This is particularly advantageous for military stealth applications, especially in environments with multi-angle and multi-site radar detection, as it can significantly enhance the stealth performance of the target. Furthermore, this dispersed power distribution can make the target's scattered signal appear as a lower signal-to-noise ratio at the radar receiver, further complicating radar detection.

5.2. Increase in Sidelobes

Sidelobes (the smaller ripples in the plot) are primarily caused by interference effects, reflecting the distribution of the beam at different angles. In the physical optics approximation, the calculation of induced currents and scattered fields is influenced by $ l $ . Increasing $ l $ introduces more phase circulation (helical structure), causing scattered waves to produce more interference, which increases the number of sidelobes. The increase in sidelobes indicates more scattered energy in certain angles, which could make it more challenging for radar to accurately locate the primary direction of target reflection.

$ {E_{side}}={E_{0}}\cdot {e^{ilϕ}}\cdot sin{(}θ) $ (9)

Mathematically, increasing $ l $ adds greater complexity to the phase variation in the electromagnetic field, resulting in more lobes in the beam at different angles. Simply put, the increased value of $ l $ complicates the electromagnetic field's distribution, leading to more reflected directions, which can significantly impact the target's stealth characteristics.

5.3. Narrowing of Power Distribution Range

For larger values of $ l $ , the phenomenon of narrowing power distribution range suggests that although the reflected power is still concentrated in certain directions (such as the main lobe), the overall energy is more evenly distributed over more angles. In other words, the difference between the power of the main lobe and sidelobes decreases, making the power distribution "smoother" in space. This uniformity in power distribution makes the target's detection characteristics less distinct on radar, effectively enhancing stealth performance.

This phenomenon has a significant impact on radar detection. Firstly, the uniformity in power distribution means that at different observation angles, the target's scattering characteristics become similar, reducing the likelihood of strong echoes at certain angles. This is especially important for stealth targets, as traditional stealth technology often relies on reducing RCS in specific directions. By applying OAM waves, the scattering energy can be evenly distributed across multiple directions, thus achieving stealth across a broader range of observation angles.

Secondly, the smoothness in power distribution reduces the signal strength detected by radar, particularly in the Doppler or angle spectrum, where it appears as increased background noise, making it harder for the radar to extract target features. As a result, OAM waves can increase the survivability of stealth targets in multi-target environments since radar systems find it more challenging to distinguish the stealth target from background noise. Additionally, the uniformity in power distribution means that the target's reflected signal lacks prominent feature patterns, further complicating identification and tracking by enemy radar systems.

Finally, the uniform scattering characteristics also have potential applications for deception and electronic countermeasures (ECM). By controlling the topological charge of the OAM wave, the scattering field distribution can be deliberately adjusted, leading enemy radar to misjudge the target's actual position and characteristics. This provides new possibilities for deception and jamming tactics, making OAM waves not only beneficial for stealth technology but also for ECM strategies.

Mathematically, this phenomenon can be understood as follows: as $ l $ increases, the helical nature of the OAM beam causes the reflected signal to become more uniformly distributed in space, reducing concentration in specific directions and enhancing stealth characteristics.

6. Conclusion

This study provides a comparative analysis of the influence of plane waves and electromagnetic vortex waves on the Radar Cross Section (RCS) and Orbital Angular Momentum Radar Cross Section (ORCS) of metallic targets, exploring the application potential of electromagnetic vortex waves in stealth technology. The results indicate that, compared to traditional plane waves, electromagnetic vortex waves, due to their unique helical phase structure and orbital angular momentum characteristics, exhibit significant differences in target scattering behavior. By varying the topological charge $l$, the spatial distribution of the reflected signal can be effectively adjusted, resulting in a more uniform energy distribution across multiple angles and reducing RCS in specific directions.

Specifically, larger values of $ l $ lead to the scattering power being evenly dispersed in space, reducing the RCS across all observation angles, thereby improving stealth performance. The even distribution of scattering power not only decreases the RCS in specific directions but also enhances the stealth performance of the target in multi-angle and multi-site radar detection environments. By smoothing out the power distribution, electromagnetic vortex waves reduce the probability of strong radar returns in certain directions, increasing the stealthiness of the target.

Moreover, the power distribution characteristics of electromagnetic vortex waves show great potential in electronic countermeasures (ECM) and deception applications. By adjusting the topological charge of OAM waves, the scattering field distribution can be deliberately altered to mislead enemy radar into misjudging the target's position and characteristics. This feature provides new possibilities for ECM and tactical deception, making electromagnetic vortex waves highly promising for future military applications.

This study also emphasizes the application of OAM waves in imaging, rotational Doppler detection, and radar sensing. Electromagnetic vortex waves exhibit unique advantages in these fields, such as enhancing target resolution, improving detection of rotational targets, and increasing selective detection capability. These characteristics make electromagnetic vortex waves not only promising for stealth technology but also advantageous for complex target identification and detection in multi-target environments.

Future research can further explore the effects of different geometries and materials on ORCS to assess the practical benefits of these advanced waveforms in radar stealth applications. Additionally, further studies on the scattering characteristics of OAM waves in complex environments and multi-target scenarios will help better understand their potential in modern warfare. By delving deeper into these phenomena, future developments could provide a theoretical basis and technical support for the next generation of high-performance radar stealth technology.

References

[1]. Y. Hong, Y. Zhao, C. Yuen and X. Qing, "A STAR-RIS with Independent 1-Bit Wave Control, " 2024 IEEE International Symposium on Antennas and Propagation and INC/USNC‐URSI Radio Science Meeting (AP-S/INC-USNC-URSI), Firenze, Italy, 2024, pp. 813-814, doi: 10.1109/AP-S/INC-USNC-URSI52054.2024.10686522.

[2]. Y. Zhao, Z. Wang, X. Xue, A. M. Ismail, X. Ma and Y. L. Guan, "Flexible Secondary Beamforming Using Holographic Meta-Surfaces for Multi-Mode Vortex Beam Transmission in Wireless Communications, " 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, Singapore, 2024, pp. 1-5, doi: 10.1109/VTC2024-Spring62846.2024.10682822.

[3]. Y. Zhao, Y. L. Guan, C. Yuen, X. Liu, A. M. Ismail and Y. Ge, "Advanced Artificial Doppler Shift Manipulation with Rotational Vortex Beams in Space-Time Digital-Coding RIS System: A Practical Approach, " 2024 IEEE VTS Asia Pacific Wireless Communications Symposium (APWCS), Singapore, 2024, pp. 1-5, doi: 10.1109/APWCS61586.2024.10679296.

[4]. Y. Zhao et al., "Near-Orthogonal Overlay Communications in LoS Channel Enabled by Novel OAM Beams Without Central Energy Voids: An Experimental Study, " in IEEE Internet of Things Journal, doi: 10.1109/JIOT.2024.3449975.

[5]. Y. Zhao, X. Ma, Y. L. Guan and X. Liu, "IF Phase Compensation and Demutiplexing for Distributed OAM Radio Receiving System, " 2024 IEEE International Conference on Communications Workshops (ICC Workshops), Denver, CO, USA, 2024, pp. 750-755, doi: 10.1109/ICCWorkshops59551.2024.10615501.

[6]. Y. Zhao et al., "2-Bit RIS Prototyping Enhancing Rapid-Response Space-Time Wavefront Manipulation for Wireless Communication: Experimental Studies, " in IEEE Open Journal of the Communications Society, vol. 5, pp. 4885-4901, 2024, doi: 10.1109/OJCOMS.2024.3439558.

[7]. D. Lin, J. Wan, J. Wang, L. Kong, Y. Zhao and Y. L. Guan, "A Novel Topology-Scale-Adaptive and Energy-Efficient Clustering Scheme for Energy Sustainable Large-Scale SWIPT-Enabled WSNs, " in IEEE Transactions on Mobile Computing, vol. 23, no. 12, pp. 13172-13188, Dec. 2024, doi: 10.1109/TMC.2024.3429235.

[8]. Y. Zhao, A. M. Ismail, G. Ju, Z. Wang, Y. Liu and Y. L. Guan, "2-bit Intelligent Reflection Surface Enhances Urban Wireless Communications: An Experimental Study, " 2024 IEEE International Workshop on Antenna Technology (iWAT), Sendai, Japan, 2024, pp. 186-189, doi: 10.1109/iWAT57102.2024.10535733.

[9]. Z. Yang, Y. Ge, Y. Zhao, Y. Fang and Y. L. Guan, "Protograph LDPC Code and Shaped Index Modulation Design for Multi-Mode OAM Systems, " in IEEE Transactions on Communications, vol. 72, no. 8, pp. 5162-5178, Aug. 2024, doi: 10.1109/TCOMM.2024.3379416.

[10]. Y. Zhao et al., "Holographic-Inspired Meta-Surfaces Exploiting Vortex Beams for Low-Interference Multipair IoT Communications: From Theory to Prototype, " in IEEE Internet of Things Journal, vol. 11, no. 7, pp. 12660-12675, 1 April1, 2024, doi: 10.1109/JIOT.2023.3334746.

[11]. M. Chen, R. Chen, Y. Zhao, Z. Yang and Y. L. Guan, "Index-Modulation OAM Detectors Resistant to Beam Misalignment, " in IEEE Transactions on Vehicular Technology, vol. 73, no. 2, pp. 2836-2841, Feb. 2024, doi: 10.1109/TVT.2023.3312295.

[12]. Z. Yang, Y. Zhao, Y. Ge, Y. Fang and Y. L. Guan, "Protograph-Based LDPC-Coded Orbital Angular Momentum Systems with Index Modulation, " 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 2023, pp. 11-16, doi: 10.1109/ICCWorkshops57953.2023.10283568.

[13]. Y. Zhao, Y. L. Guan, Z. Yang, G. Ju and Y. Lu, "Vortex Beams Enhance IRS-Aided Low-Rank Channel Transmission: Principle and Prototype, " ICC 2023 - IEEE International Conference on Communications, Rome, Italy, 2023, pp. 883-888, doi: 10.1109/ICC45041.2023.10279703.

[14]. Y. Zhao, Z. Wang, Y. Lu and Y. L. Guan, "Multimode OAM Convergent Transmission With Co-Divergent Angle Tailored by Airy Wavefront, " in IEEE Transactions on Antennas and Propagation, vol. 71, no. 6, pp. 5256-5265, June 2023, doi: 10.1109/TAP.2023.3263920.

[15]. Y. Zhao, G. Ju, Z. Yang, Y. Ge, Y. Lu and Y. L. Guan, "Orbital Angular Momentum Transmission Based on Satellite Formation Relay in Space Communications, " 2022 Asia-Pacific Microwave Conference (APMC), Yokohama, Japan, 2022, pp. 913-915, doi: 10.23919/APMC55665.2022.10000035.

[16]. Y. Zhao et al., "OAM-based Reconfigurable Doppler Shifts Enable PAPR Reduction for Multi-carrier Doppler Diversity, " 2022 Asia-Pacific Microwave Conference (APMC), Yokohama, Japan, 2022, pp. 485-487, doi: 10.23919/APMC55665.2022.9999832.

[17]. Y. Zhao, Y. Lu, Y. L. Guan, Q. Wu and C. Zhang, "Flexible Self-Alignment Reception for OAM-Based Large-Capacity Wireless Backhaul Links, " 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI), Denver, CO, USA, 2022, pp. 1970-1971, doi: 10.1109/AP-S/USNC-URSI47032.2022.9886596.

[18]. C. Zhang, X. Jiang and Y. Zhao, "Efficient Instantaneous Channel Propagation Modeling for Aeronautical Communications Systems With Compressed Sensing, " in IEEE Transactions on Antennas and Propagation, vol. 70, no. 2, pp. 1211-1220, Feb. 2022, doi: 10.1109/TAP.2021.3111499.

[19]. Y. Zhao and C. Zhang, "Distributed Antennas Scheme for Orbital Angular Momentum Long-Distance Transmission, " in IEEE Antennas and Wireless Propagation Letters, vol. 19, no. 2, pp. 332-336, Feb. 2020, doi: 10.1109/LAWP.2019.2962199.

[20]. C. Zhang, J. Jiang, Y. Zhao and X. Jiang, "New Degrees of Freedom for Beamforming Manipulation in MIMO Transmission with OAM, " 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 2019, pp. 1-6, doi: 10.1109/GCWkshps45667.2019.9024467.

[21]. Y. Zhao and C. Zhang, "Compound Angular Lens for Radio Orbital Angular Momentum Coaxial Separation and Convergence, " in IEEE Antennas and Wireless Propagation Letters, vol. 18, no. 10, pp. 2160-2164, Oct. 2019, doi: 10.1109/LAWP.2019.2939345.

[22]. C. Zhang and Y. Zhao, "Orbital Angular Momentum Nondegenerate Index Mapping for Long Distance Transmission, " in IEEE Transactions on Wireless Communications, vol. 18, no. 11, pp. 5027-5036, Nov. 2019, doi: 10.1109/TWC.2019.2927672.

[23]. Y. Zhao, P. Xu and C. Zhang, "Orbital Angular Momentum Waves Multiplexing Transmission Experiment Based on Pseudo-Coplanar Scheme, " ICC 2019 - 2019 IEEE International Conference on Communications (ICC), Shanghai, China, 2019, pp. 1-6, doi: 10.1109/ICC.2019.8762013.

[24]. C. Zhang, J. Jiang and Y. Zhao, "Euclidean Space with Orbital Angular Momentum, " 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 2019, pp. 1-6, doi: 10.1109/ICCW.2019.8756875.

[25]. M. ZHU, Y. ZHAO, C. ZHANG and Y. PIAO, "High Precision Positioning for Searching Airborne Black Boxes Underwater Based on Acoustic Orbital Angular Momentum, " 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 2018, pp. 1-9, doi: 10.1109/DASC.2018.8569848.

[26]. H. Wu, Y. Zhao and C. Zhang, "Efficient Hemisphere Unambiguous Magnetic Positioning for Helmet Mounted Sights, " 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 2018, pp. 1-6, doi: 10.1109/DASC.2018.8569882.

[27]. Y. Zhao, J. Jiang, X. Jiang and C. Zhang, "Orbital angular momentum multiplexing with non-degenerate modes in secondary frequency domain, " 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 2018, pp. 1-4, doi: 10.1109/IEEE-IWS.2018.8400970.

[28]. X. Jiang, Y. Zhao and C. Zhang, "Capacity evaluation on the long-distance orbital angular momentum non-orthogonal transmission, " 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 2018, pp. 1-4, doi: 10.1109/IEEE-IWS.2018.8400839.

[29]. J. Li et al., "Codebook Design for Uniform Rectangular Arrays of Massive Antennas, " 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2013, pp. 1-5, doi: 10.1109/VTCSpring.2013.6692478.

Cite this article

Xu,C. (2025). Advanced Scattering Analysis of Targets under Plane Waves and Electromagnetic Vortex Waves for Stealth Applications. Theoretical and Natural Science,79,85-93.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of the 4th International Conference on Computing Innovation and Applied Physics

ISBN：978-1-83558-897-0(Print) / 978-1-83558-898-7(Online)

Editor：Ömer Burak İSTANBULLU, Marwan Omar, Anil Fernando

Conference website: https://2025.confciap.org/

Conference date: 17 January 2025

Series: Theoretical and Natural Science

Volume number: Vol.79

ISSN：2753-8818(Print) / 2753-8826(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).