1. Introduction

Time series analysis is an important analytical method that plays a key role in many fields of scientific research and practical applications today. Financial markets and biological phenomena are two fields of great research value and practical significance. Time series analysis provides a powerful tool for a deeper understanding of the dynamic changes in these two fields[1].

The fluctuations and changes in financial markets are highly complex and uncertain. Financial data such as the rise and fall of stock prices and changes in exchange rates are typical time series. Time series analysis can uncover the underlying patterns in financial data and provide a basis for decision-making for investors, financial institutions and policymakers. Accurately predicting the trend of stock prices and exchange rates and effectively measuring financial risks are crucial to maintaining the stability of financial markets and promoting economic development.

Biological phenomena also involve a large amount of time series data. From the growth and development process of organisms to changes in biomedical signals, they all show characteristics of changes over time. For example, the growth curves of animals and plants, the dynamic changes in microbial populations, and biomedical signals such as electrocardiograms and brain electrical signals can all reveal their inherent laws and mechanisms through time series analysis. This is of great significance for gaining a deeper understanding of life phenomena, improving medical diagnosis, and promoting the development of biological sciences[2].

2. Basic theory of time series analysis

2.1. Concepts and characteristics of time series

The concepts and characteristics of time series are shown in Table 1.

Table 1: Concepts and characteristics of time series

2.2. Common time series models

The autoregressive model (AR) is a common time series model. It predicts the current value by using the time series values of the same variable in the past. Its mathematical expression is

.

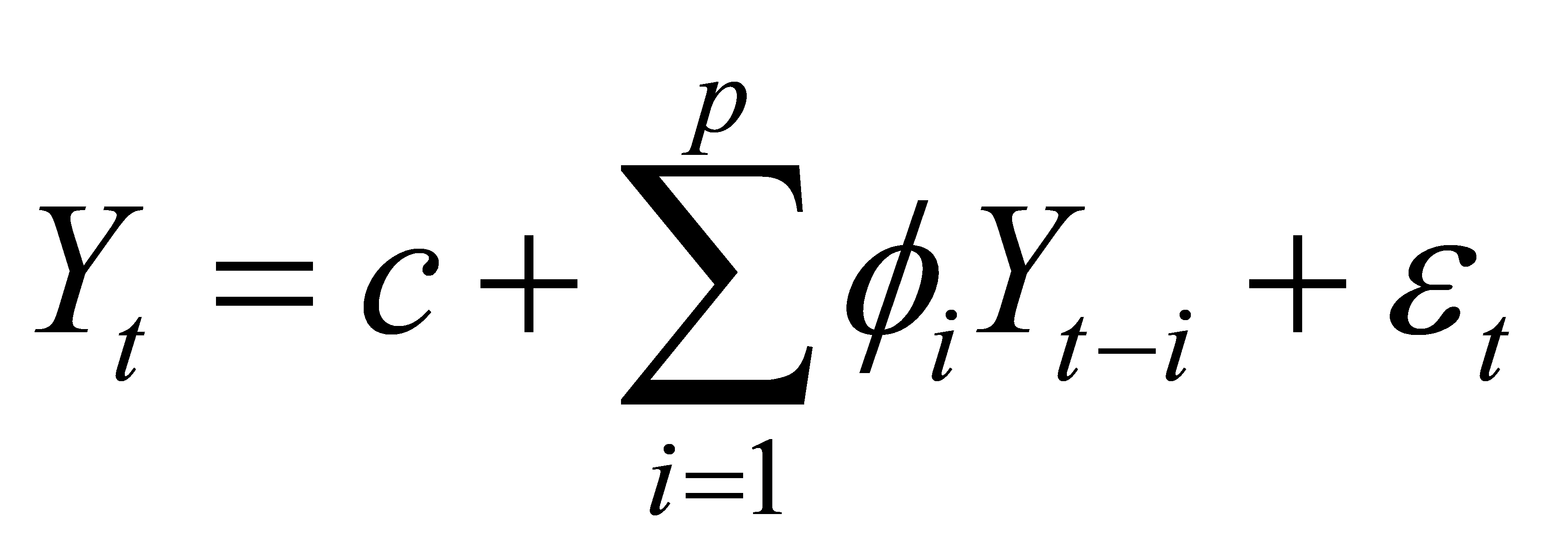Y represents the value at the current moment, c is a constant term, p; is the autoregressive coefficient, Y-i is the value at different past moments, p indicates the order of the model, and ét is the random error term. The core idea of the autoregressive model is that there is a linear relationship between the current value and the values at several past moments, By weighted summation of past values and adding a random disturbance term, the current value is predicted. In practical applications, an appropriate order needs to be determined according to the specific data situation to improve the prediction accuracy of the model[3].

The moving average model (MA) expresses the current value as a linear combination of the current and past random error terms. Its mathematical expression is

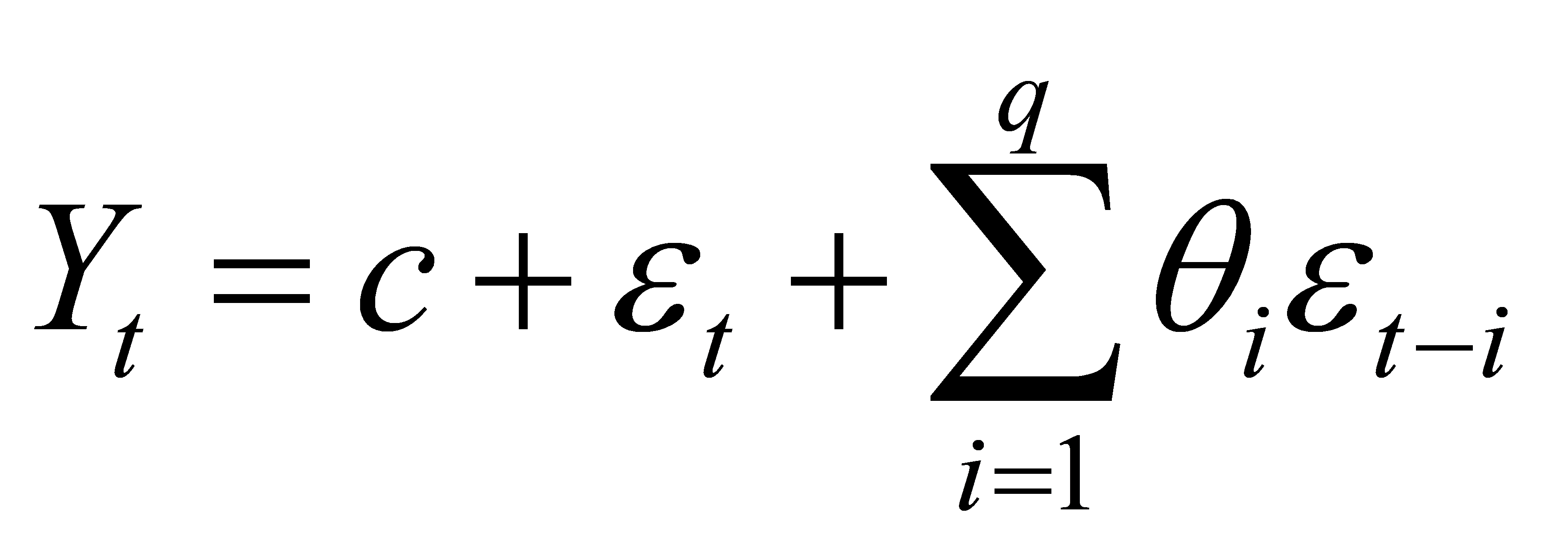
the current random error term, 0, is the moving average coefficient, g is the order of the model, and ét-i is the past random error term, The moving average model mainly focuses on the influence of random error terms and describes the change of the current value by weighted summation of random error terms at different moments The autoregressive moving average model (ARMA) combines the characteristics of the autoregressive model and the moving average model. It considers both the autocorrelation of the time series and the influence of iY-i+etrandom error terms.

3. Time series analysis in financial markets

3.1. Characteristics of financial time series

Financial time series possess several distinct characteristics. Firstly, volatility is a prominent feature. The values of financial instruments like stocks, bonds, currencies, and others frequently experience significant fluctuations. Prices can change rapidly and in an unpredictable manner.

Financial time series are often non-stationary. The statistical properties such as mean and variance can change over time. This poses a challenge as traditional statistical methods typically assume stationarity.

The presence of fat tails. The distribution of returns in financial time series usually has fatter tails compared to a normal distribution. This implies that extreme events occur more frequently than would be expected under a normal distribution.

There is often a certain degree of correlation between values at different times. This can be attributed to various factors including market trends, economic cycles, and investor sentiment.

The variance of financial time series is often not constant over time. This means that the volatility of financial markets can change, making risk management more difficult.

3.2. Applications of Time Series Analysis in the Stock Market

Time series analysis plays a crucial role in the stock market. One of its main applications is in stock price prediction. By analyzing historical stock price data using time series models such as autoregressive (AR), moving average (MA), and autoregressive integrated moving average (ARIMA), it is possible to forecast future stock prices. This helps investors make informed decisions about buying, selling, or holding stocks[4].

Risk management is another important application. Time series analysis can be used to measure the volatility of stock prices. Models like the generalized autoregressive conditional heteroskedasticity (GARCH) can capture the changing volatility over time and help investors assess the risk associated with their stock investments.

Moreover, time series analysis can also be used to identify trends and patterns in the stock market. For example, it can detect bullish or bearish trends, as well as seasonal patterns or cycles. This information can be valuable for traders and portfolio managers in formulating their investment strategies.

In addition, time series analysis can help in analyzing the impact of economic and financial events on stock prices. By studying the relationship between stock prices and various economic indicators or news events using time series techniques, investors can better understand the market dynamics and make more accurate predictions[5].

3.3. Applications of Time Series Analysis in the Foreign Exchange Market

Time series analysis is highly valuable in the foreign exchange market. One significant application is in exchange rate forecasting. By analyzing historical exchange rate data using time series models such as ARIMA or GARCH, it is possible to predict future exchange rate movements. This is crucial for businesses engaged in international trade, as it helps them manage currency risk and plan their financial operations.

Measuring volatility is essential for investors and risk managers, as it helps them assess the uncertainty and potential losses associated with currency fluctuations. Models like GARCH can capture the time-varying volatility of exchange rates and provide insights into market conditions.

Furthermore, time series analysis can help identify trends and patterns in the exchange rate market. For instance, it can detect long-term trends, short-term fluctuations, and seasonal patterns. This information can be used by traders and policymakers to make informed decisions.

In addition, time series analysis can be employed to analyze the impact of economic and geopolitical events on exchange rates. By studying the relationship between exchange rates and factors such as interest rates, inflation, political stability, and trade policies, it is possible to understand how these events influence currency values. This knowledge can help policymakers formulate appropriate monetary and fiscal policies to stabilize the exchange rate[6].

4. Application of time series analysis to biological phenomena

4.1. Characteristics of Biological Time Series

Biological time series have several unique characteristics. Firstly, they often exhibit periodicity. Many biological processes, such as circadian rhythms, menstrual cycles, and seasonal changes in animal behavior or plant growth, follow regular patterns over time.

Biological time series can be highly variable and stochastic. Biological systems are complex and subject to a wide range of internal and external influences, leading to variability in the measured data. Random fluctuations and noise are common in biological time series, making it challenging to extract meaningful patterns[7].

Another characteristic is non-stationarity. Biological processes can change over time due to factors such as development, aging, disease, or environmental changes. This means that the statistical properties of biological time series may not be constant and may require specialized methods for analysis.

For example, in physiological systems, various organs and biochemical pathways interact to regulate bodily functions. Analyzing these complex interactions requires advanced time series analysis techniques.

Understanding the role of these factors in shaping biological time series is essential for studying the mechanisms of biological processes and for developing personalized medicine and interventions.

4.2. Applications of Time Series Analysis in Biological Growth and Development

Time series analysis has several important applications in understanding biological growth and development. One of the key uses is in modeling and predicting the growth curves of organisms. By analyzing time series data on the size, weight, or other growth-related parameters of plants, animals, or microorganisms over time, researchers can develop mathematical models that describe the growth process. These models can help in understanding the factors that influence growth and in making predictions about future growth.

Time series analysis can also be used to study the dynamics of developmental processes. For example, it can be applied to analyze the progression of embryonic development, metamorphosis, or aging. By tracking changes in specific biological markers or morphological features over time, researchers can gain insights into the underlying mechanisms of development and identify critical stages or transitions[8].

In addition, time series analysis can help in understanding the effects of environmental factors on growth and development. By correlating time series data on biological growth with environmental variables such as temperature, humidity, light, or nutrient availability, researchers can determine how these factors influence the growth and development of organisms. This information can be useful for optimizing growth conditions in agriculture, aquaculture, or biotechnology.

Time series analysis can be combined with other techniques such as genomics or proteomics to study the molecular mechanisms underlying growth and development. By integrating time series data on gene expression, protein levels, or metabolite concentrations with growth parameters, researchers can identify key regulatory pathways and genes that are involved in the growth and developmental process.

5. Conclusion

In conclusion, time series analysis has demonstrated significant applications in both financial markets and biological phenomena. In the financial domain, it helps with stock price prediction, risk management, and understanding market trends. In the realm of biology, it plays a crucial role in analyzing growth and development, studying environmental impacts, and uncovering molecular mechanisms.

As we continue to advance in technology and research methods, the potential for time series analysis in these areas will only grow. It offers valuable insights for decision-makers in finance and for scientists seeking to understand the complexity of life. Future research should focus on improving the accuracy and robustness of time series models, exploring new applications, and integrating multiple data sources to gain a more comprehensive understanding.