Lean- Mathematical Formal Proof Tools and AI Automated  Proofs

Yiyang Zou

doi:10.54254/2753-8818/2025.21398

1. Introduction

1.1. Background of automatic proving

Mathematical proof automation refers to the process of using computer programs and algorithms to automatically complete mathematical proofs, which involves the proof of theorems, the selection of proof strategies, and the generation of proof processes. With the development of mathematics, people gradually realize that mathematical proof is particularly important in the development of mathematics, to improve the efficiency and accuracy of mathematical proof, it reduces the burden of mathematicians, and promotes the development and innovation of the discipline, mathematicians have invested more and more energy into the realization of mathematical automatic proof.

1.2. Background of lean's emergence

The two most important properties of mathematics, correctness and rigor, are facing threats. Mathematics, as a subject with extremely high threshold and rich content, is difficult for both professional mathematicians and amateur math enthusiasts to master every field of mathematics, especially the relatively specialized theorems and proofs in mathematics. People have little exposure to these theorems and proofs. Since people rarely met these contents, is there a possibility that a mathematical theorem or proof may have problems? In fact, people always make mistakes, and the possibility of errors occurring is evident in the limited exposure to such content. And if people learn and develop based on a wrong theory. So, all the results obtained will be invalid, which will have a devastating impact on the mathematical community. In this environment, mathematicians urgently need a tool that can express mathematical proofs in a standardized way, and lean emerged in this environment.

This paper will give a detailed introduction to mathematical formal proofs and mathematical automated proofs, explore the bright prospects of the combination of mathematical formal proofs and AI technologies, and summarize the existing development process and future development directions. It mainly focuses on the unique advantages of lean compared with other mathematical formal languages, such as powerful type system, built-in proof capabilities, and people's two attempts at automatic proof of mathematics, the use of chain of thought model, i.e., the birth of o1 and o3, and the development and use of lean copilot. The future prospect of realizing mathematical automated proofs will be analyzed from two directions: difficulties and development.

2. Literature review

2.1. The development of formal proof tools

In the mid-20th century, the introduction of the Resolution Principle and Herbrand's Theory laid the foundation for formal proofs. In the 1970s and 1980s, multiple important theorems proving tools emerged, such as Coq and Isabelle, which became popular and supported interactive proofs. Since the 2000s, the application of dependency type theory in formal proofs has been increasing, allowing users to define more complex structures and functions, define mathematical objects and their properties more accurately, and express complex logical relationships through types. Lean is one of the representatives among them. [1]

2.2. What is Lean?

Lean has a bright future in the fields of computer programming languages and formal mathematics. It is an open-source project developed by Microsoft Research in 2013, which is not only a powerful functional programming language but also an interactive theorem prover. It enables the representation of proof process in computer language while simplifying the process of writing proofs [2].

As shown in Figure 1 below, Lean is an important tool for formalizing mathematical proofs, serving as a bridge between formal theorems and formal proofs. It integrates computer programming with mathematical logic, providing new directions and injecting new vitality into the combination of mathematics and AI.

In recent years, the field of mathematical logic has gradually formed a consensus on Curry Howard isomorphism, as the famous slogan goes: Proposition=type, proof=program [3]. The Curry Howard isomorphism establishes a channel between mathematical proofs and computer programming. Lean’s core principle is based on currying, a functional programming transformation method for handling multivariate functions. It refers to transforming a function from a callable f (a, b, c) to a callable f (a) (b) (c), improving the applicability of the function [4].

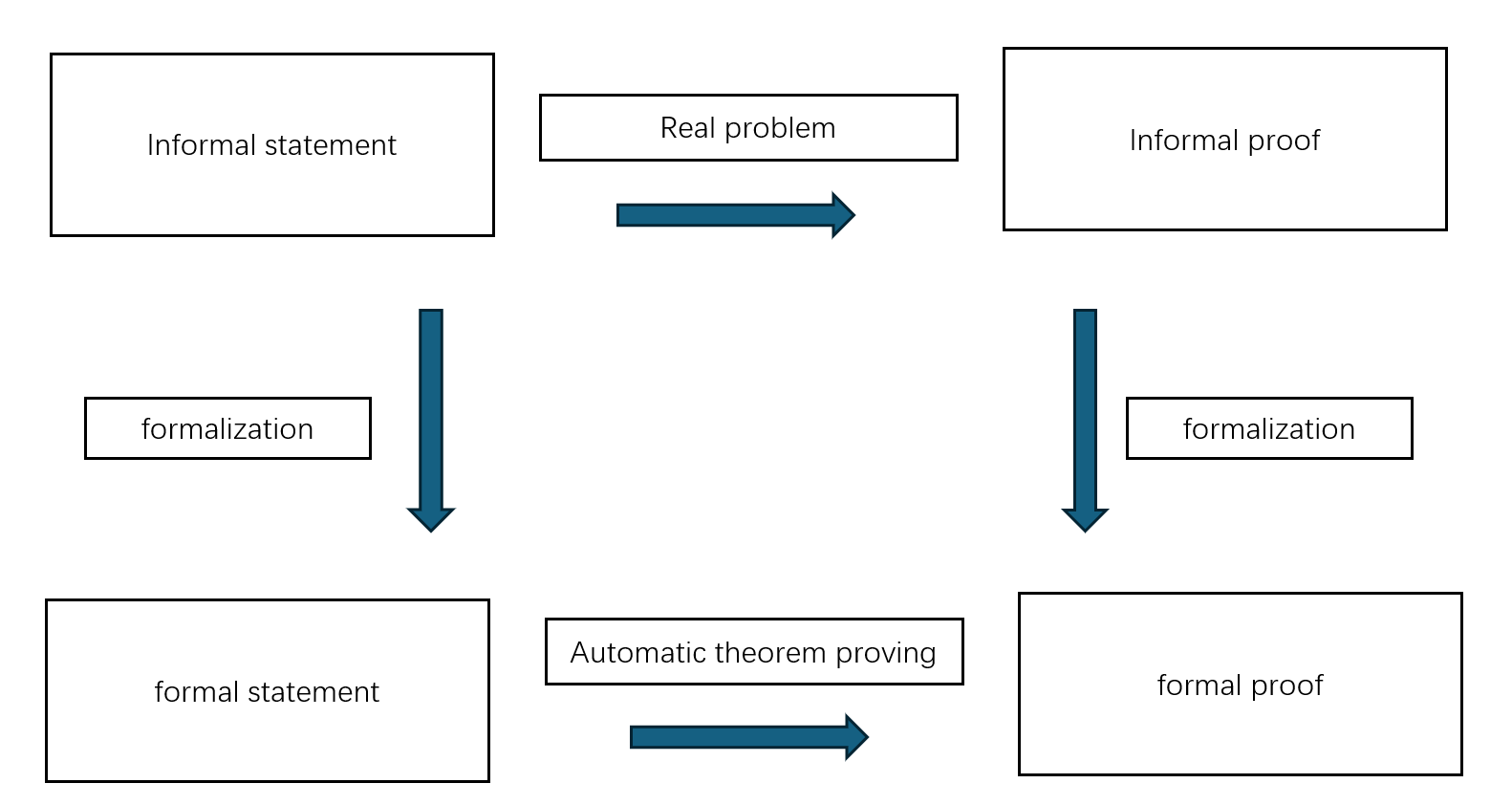
/word/media/image1.png

Figure 1: Illustration of a mathematical formal proof

2.3. Characteristics of Lean

Among many functional languages, lean stands out for its remarkable features. Compared to traditional functional languages such as OCaml or Haskell, Lean4 provides a more powerful type system and built-in proof capabilities. Compared with other theorem provers such as Coq and Agda, Lean4 has significant advantages in terms of resources, databases, and usability [5].

Lean 4 possesses several core features that make it stand out. It adopts dependent type theory, allowing types to depend on values, which is extremely important in formal proofs. Its powerful built-in axiom system supports type classes and type constructors, making it easier to construct complex mathematical theories. As a pure functional language, Lean4 emphasizes a programming style without side effects, benefiting parallel computing and formal verification. Lean4 is also intelligent, capable of omitting certain theorem proofs and providing features such as automatic pairing, searching, and suggesting. With a rich resource library, including more than seventeen proven theorems and a systematic teaching and theorem query system, Lean4 offers robust support for learning and research. Despite the complexity of its type system, Lean4 achieves efficient code generation through a carefully designed compiler, demonstrating both high performance and practicality.

3. Automating Proofs in Lean and Mathematical Theorems

3.1. The Use of Lean Copilot

Lean Copilot is a plugin designed specifically for the Lean environment, utilizing large language models (LLMs) to automate tasks such as proof strategy recommendations, premise selection, and proof search, enabling collaboration between humans and LLMs to infer formal mathematical proofs. This tool allows users to utilize LLM for proof automation in Lean, such as proposing proof steps, searching for proofs, and selecting relevant premises [6]. Lean Copilot addresses a core technical challenge: enabling LLM inference to run within the Lean environment. Its main functions can be broadly categorized into four areas. Firstly, Tactic Suggestion, where Lean Copilot dynamically provides proof strategy recommendations to assist users in selecting appropriate steps during the proof process. Secondly, Proof Search, which integrates LLM-generated strategies with existing automated tools like AESOP to perform multi-step proof searches. Additionally, Premise Selection intelligently filters and identifies necessary prerequisites to facilitate proof construction. Lastly, Model Execution allows direct execution of any LLM inference within Lean, enabling customized application development [7]. On April 18, 2024, California Institute of Technology professor Anima Anandkumar announced that the team has released an extended version of Lean Copilot's paper and updated the code repository. According to research data, proof search can automatically complete approximately 81.2% of the proof steps in the theorem [8].

The significance of Lean Copilot is mainly reflected in the following aspects:

• Accelerate the proof process: Lean Copilot can significantly speed up the proof of mathematical theorems by providing strategy suggestions, searching for proofs, and selecting premises. For example, in some experiments, it can increase the speed of the proof process by several times.

• Reduce manual intervention: Traditional mathematical proofs rely on manual deduction, requiring a significant amount of time and effort for verification and modification. Lean Copilot can automate many proof steps, reducing the manual intervention of mathematicians and theoretical computer scientists in complex proof processes.

• Balancing machine and human intelligence: Lean Copilot allows users to seamlessly intervene and modify the proof process when necessary, providing a balanced collaboration between machine automation and human intuition. This human-machine collaboration mode can better leverage their respective advantages, improve the accuracy and reliability of proof.

• Start positive feedback loop: By running LLM inference in Lean, Lean Copilot expects to start a positive feedback loop: automated proof will generate better data, thereby improving LLM's mathematical performance.

3.2. Outlook on the Implementation of Automated Proof of Mathematical Theorems in the Future

With the development of mathematics in modern society, it has become more abstract and logical, no longer focusing on solving problems in real life, but exploring the deep logic and essence behind numbers. This also means that people have higher requirements for the proof of theorems at the bottom of mathematics. Therefore, the formalization of mathematical proofs and their combination with computer technology have important applications, and there will be many challenges in achieving formal proofs.

The Challenge of Formal Proof

• The learning curve is steep: Formal proof requires expressing complex mathematical concepts in rigorous computer and logical languages. While obtaining a scientific and rigorous proof process, it can also make mathematical thinking more cumbersome and complex, especially for high-level abstract concepts. The process of formal expression may become extremely complex and lengthy, increasing the difficulty of writing and understanding

• Complex verification and detail review: Formal proofs have higher verifiability, but it also means that every detail needs to be carefully reviewed and confirmed, especially when dealing with complex mathematical structures [9]. Researchers need to put in extra effort to ensure that each step is correct

• Requires manual intervention: Limited automatic reasoning ability relies on user provided prompts and structures when dealing with complex mathematical problems, insufficient coverage of knowledge and theorems in specific fields, and may not generate effective proofs when facing highly complex or non-standard propositions, requiring more manual intervention and guidance

In summary, mathematics holds an irreplaceable core position in the development of human civilization, and the development of formal proof tools has provided new perspectives and methods for mathematical research. Although it still faces some challenges, it has shown great potential in improving the accuracy and rigor of mathematical research, promoting the deep integration of mathematics and computer science. Formal mathematical proof plays an increasingly important role in the development of AI technology. Realizing AI's autonomous reasoning will enable us to better solve mathematical problems and greatly improve mathematical technology, thus playing a greater role in various fields

4. Conclusion

As society continues to progress, mathematics and computer technology are being widely applied in an increasing number of fields. Meanwhile, the development of computer and mathematical technologies has become an important force in driving social progress. Faced with this challenge, mathematicians have begun to explore the foundation of mathematics—mathematical proofs—and have attempted to use computer languages to standardize the writing of mathematical proofs in order to reduce errors and facilitate subsequent use and verification. The emergence of formal mathematical languages such as Lean is precisely to solve this problem.

Through the research and development of mathematical formal languages, some mathematicians have started to consider the development of automated mathematical proofs. As the prospects and wide applications of automated mathematical proofs are drawing more and more attention, the process of achieving mathematical proof automation has also encountered many difficulties. For example, the logical conflicts between large language models (LLMs) and mathematical formal proofs have led to unsatisfactory integration effects, and the excessive proportion of manual intervention in the proof process. However, through the joint efforts of mathematicians and computer scientists, many of these problems have been resolved to varying degrees.

These advancements indicate that the realization of automated mathematical proofs will inject new vitality and bring innovation to the development of mathematics, computer science, and even the global scientific and technological community.

References

[1]. Blass, A. (2016). Symbioses between mathematical logic and computer science. Annals of Pure and Applied Logic, 167(10), 868-878. https://doi.org/10.1016/j.apal.2014.04.018

[2]. Lean Documentation Overview. Lean. https://lean-lang.org/lean4/doc/

[3]. Harvard School of Engineering and Applied Sciences. (2010). Lecture 19: Type inference; Curry-Howard isomorphism. Computer Science 152. https://groups.seas.harvard.edu/courses/cs152/2010sp/lectures/lec19.pdf

[4]. Wei, J., Schuurmans, D., Bosma, M., Weng, L., et al. (2022). Chain-of-thought prompting elicits reasoning in large language models. arXiv. https://doi.org/10.48550/arXiv.2201.11903

[5]. GeeksforGeeks. What is currying function in JavaScript? https://www.geeksforgeeks.org/what-is-currying-function-in-javascript/

[6]. Song, P. Lean Copilot: LLMs as copilots for theorem proving in Lean. GitHub. https://github.com/lean-dojo/LeanCopilot/blob/main/README.md

[7]. Ruan, R.Y. (2024). Open-source highlight: Lean Copilot – Leading the innovation in theorem proving. CSDN. https://blog.csdn.net/gitblog_01057/article/details/141013426 (In Chinese)

[8]. Song, P.Y, Yang, K.Y, & Anandkumar, A. (2024). Towards large language models as copilots for theorem proving in Lean. arXiv. https://arxiv.org/pdf/2404.12534

[9]. Tencent News. (2024, October 8). Tao Zhexuan’s latest interview: The comparison of OpenAI o1 to "a mediocre but not completely incompetent graduate student" was misunderstood. Tencent News. https://news.qq.com/rain/a/20241008A04U8C00 (In Chinese)

Cite this article

Zou,Y. (2025). Lean- Mathematical Formal Proof Tools and AI Automated Proofs. Theoretical and Natural Science,92,31-35.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of the 3rd International Conference on Mathematical Physics and Computational Simulation

ISBN：978-1-83558-973-1(Print) / 978-1-83558-974-8(Online)

Editor：Marwan Omar

Conference website: https://2025.confmpcs.org/

Conference date: 27 June 2025

Series: Theoretical and Natural Science

Volume number: Vol.92

ISSN：2753-8818(Print) / 2753-8826(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).