1. Introduction

In the existing AES (Advanced Encryption Standard) encryption principle, each round of encryption can be divided into four main parts of the operation: SubBytes, ShiftRows, MixColumns and AddRoundKey, which uses the key only in the last step AddRoundKey, that means, the security from password is only guaranteed by this step, the other steps are mainly contributing to obfuscate the encrypted bytes corresponding to the plaintext, but the deciphering of those steps don’t rely on any password. This means that the encryption effect of the first three steps can be removed by finite steps of processing on computer, and the security of the encryption itself should not be guaranteed by the complexity of the encryption method, so it can be determined that there is still room for optimization here.

Inspired by the high dimensional Rubik's Cube, in this paper, a new way of encryption is found, which gives an algorithm that relies on symmetric keys to generate encrypted matrices by matrix rotation. This is capable of upgrading the security of the existing encryption principle of AES. Like AES maps the whole byte into a 2-dimensional ByteMatrix, the optimization proposed in this paper will map the whole byte to a 4-dimensional fourth-order matrix, and use the idea of rotating (similar to the Rubik's Cube) to define a new "Rotate" and "Exchange" encryption, and then determine the encryption sequence through the password to ensure its security. The encryption sequence depends on a password to ensure its security and effectiveness. This part of the research is implemented and debugged on Python. Through the model proposed in this paper, it will be able to improve the original encryption effect and confidentiality level of AES with more keys, ensure the effectiveness of other encryption steps, and reduce the risk of information leakage.

2. Decipherability analysis of the original SubBytes

2.1. Mathematical evidence of commutative reversibility and feasibility of inverse commutative summation

The AES encryption algorithm establishes a bijection between bytes during SubByte by means of a fixed S-box, which in turn disrupts the correspondence of the bytes to their original positions [1]. A is the byte matrix before SubByte, and S is the one-to-one correspondence transformation performed by the S-box:

\( S(A)↦B \) (1)

B represents the swapped byte matrix. However, since the S-box is publicly and uniquely determined, it is straightforward to find a fixed inverse mapping \( {S^{-1}} \) in both normal decryption and unconventional deciphering:

\( {S^{-1}}(B)↦A \) (2)

For a state byte matrix, if the result of a SubByte step is subjected to the inverse SubByte operation \( {S^{-1}} \) , the result of that SubByte encryption step will be recovered. This is a threat to the overall security of AES encryption, as will be demonstrated below.

2.2. Ciphertexts handling and the possibility of corresponding key failure

As a symmetric encryption, all the processing in AES encryption is reversible. Except for AddRoundKey, all the steps in AES can be cracked directly without a password, that is, the corresponding position of the relationship can be worked out before the password is hacked. There’s a round of encryption as an example:

\( {A_{i}}⊕{K_{i}}={B_{i}},C∘R∘S({B_{i}})={P_{i}},{P_{i}}⊕{W_{i}}={A_{i+1}} \) (3)

Here is the operation performed for one single round of encryption, \( {K_{i}} \) is the round key (unknown to the decryptor), R is the ShiftRows transformation, C is the MixColumns transformation, and \( {W_{i}} \) is the new round key obtained by the processing of K, which is set temporarily:

\( {W_{i}}=W({K_{i}}) \) (4)

Then it follows from the fact that their inverse operations all exist and are unique:

\( {A_{i+1}}⊕W({K_{i}})={P_{i}},{S^{-1}}∘{R^{-1}}∘{C^{-1}}({P_{i}})={B_{i}},{B_{i}}⊕{K_{i}}={A_{i}} \) (5)

The equation in the previous line can be verified by the principle of superposition of inverse maps and the self-reflexivity of the Exclusive OR. However, if \( {K_{i}} \) is in an unknown state during the deciphering process, the above steps should be easily reordered:

\( {Q_{i}}=((C∘R∘S{)^{-1}}({A_{i+1}}) \)

\( f({A_{i+1}},{K_{i}})=(C∘R∘S{)^{-1}}(W({K_{i}}))⊕{Q_{i}})⊕{K_{i}}={A_{i}} \) (6)

This method provides an operation to reset the position of the disrupted bytes without a password, which can eliminate the effect of all the disruptions in the encryption, in order to prepare for the decryption step that requires a key. However, the remaining part of the key decryption will also face the problem of "the corresponding position of the key does not match the ciphertext", because each round of key stacking is for the encrypted byte matrix after the disruption, so it can not be directly substituted. However, the keys can also be pretreated like those byte matrix do in the opposite order of encryption, and ultimately a transposition function can be given out, after whose pretreatment the encrypted byte matrix only needs to add those keys in the correct order:

\( {Re_{i}}({K_{i}})=(C∘R∘S{)^{l-i}}({K_{i}}),{Re_{i}}({W_{i}})=(C∘R∘S{)^{l-i}}(W({K_{i}})) \) (7)

After substituting the key, this function will solve a pretreated key

Sequence, which can decrypt the plaintext by perform XOR summation operations with the byte matrix in the inverted order:

\( T({A_{n}})=(C∘R∘S{)^{n-1}}({A_{n}}) \)

\( g({A_{n}},\lbrace {K_{1}},…,{K_{n}}\rbrace )={e_{1}}(W({K_{1}}))⊕{Re_{1}}({K_{1}})={A_{1}} \)

\( =T({A_{n}})⊕{Re_{n}}(W({K_{n}}))⊕{Re_{n}}({K_{n}})⊕…⊕R \) (8)

To the matrix after transposed, the security is at the same level as there’s only AddRoundKey step in the encryption. And all those keys in different rounds are combined with the different-or-sum operation, which means the number of rounds can’t increase the security. So it is envisioned that the step of SubBytes can also be encrypted in order to protect the degree of security.

2.3. Effect of security enhancement by adding SubBytes key

The reason that the method above can create an inverse mapping for those encryption steps in AES and pretreat the encryption results for batch decryption is that the transforms used for its disruption are same and unique, and if each round is disrupted with a different S-Box or other method that relies on another key, it will make the new inverse computation extremely complex and will also need to rely on a new key. Let the hall permutation transformation of round i be \( R{o_{i}}({A_{i}}) \) :

\( R{o_{i}}({A_{i}})=C∘R∘{S_{i}}({A_{i}}) \) (9)

\( {S_{i}} \) is a key-dependent SubByte transformation, then the previous decryption formula should be changed to:

\( {T^{ \prime }}({A_{n}})=(\prod _{i=1}^{n} R{o_{i}})({A_{n}}),Re_{1}^{ \prime }({K_{1}})={K_{1}},Re_{i}^{ \prime }=(C∘R∘{S_{i}}{)^{-1}}∘Re_{i-1}^{ \prime } \)

\( {g^{ \prime }}({A_{n}},\lbrace {K_{1}},…,{K_{n}}\rbrace )={A_{1}} \)

\( ={T^{ \prime }}({A_{n}})⊕Re_{n}^{ \prime }(W({K_{n}}))⊕Re_{n}^{ \prime }({K_{n}})⊕...⊕Re_{1}^{ \prime }(W({K_{1}}))⊕Re_{1}^{ \prime }({K_{1}}) \) (10)

And each round of \( R{o_{i}} \) and \( R{e_{i}} \) here depends on the transformation key. This leads to a new model in which it is not possible to preprocess the matrices to eliminate the permutation transforms without the key. And the reason for using fixed permutation transforms for encryption in AES is that complex 16*16 permutation bijection is difficult to generate in bulk. In the following section, we will give an idea of permutation transforms based on Rubik's Cube disrupted by algorithm, which can realize key dependent permutation encryption transformation.

3. Feasibility proof of 4-dimensional dot matrix corresponding to byte

3.1. 4-dimensional rotation effect

The rotating transform of a 16*16 byte matrix leads to a very similar result because of the simple structure of a 2-dimensional matrix; and a 3-dimensional matrix is very difficult to establish correspondence with the byte due to its quantitative peculiarities ( \( {3^{k}}≠256,k∈Z \) ). Compared to a 16*16 2-dimensional matrix or a 3-dimensional matrix structure, a 4-dimensional fourth-order matrix can both correspond one-to-one with 256 bytes and provide sufficient complexity for rotation-based disruption. An attempt is made to construct a 4-dimensional 4*4*4*4 node-square matrix to correspond to 256 different bytes.

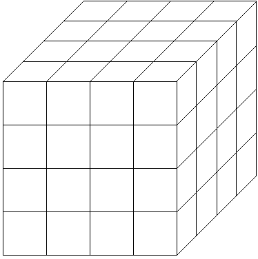
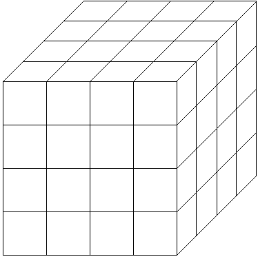
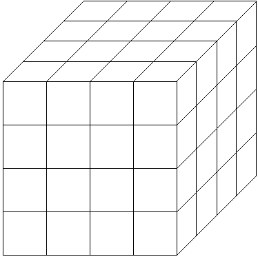
A1 A2 A3 A4

Figure 1: Schematic diagram of a 4-dimensional fourth-order matrix

As shown in Fig. 1, the 4th order 4-dimensional matrix A can be interpreted as a vector consisting of four 4th order 3-dimensional matrices \( {A_{1}},{A_{2}},{A_{3}},{A_{4}} \) , with an extra dimension orthogonal to all the original directions on top of the 3-dimensional matrix. Define the new center-symmetric coordinates for each element of this high-dimensional matrix, such as the element \( a={A_{1}}(-1,1,2) \) in A1 (the center-symmetric coordinates are used here for the convenience of rotational transformation afterwards), and then define the coordinates corresponding to \( {A_{1}},{A_{2}},{A_{3}},{A_{4}} \) in the new dimension to be -2,-1,1,2, respectively, so that there is \( a={A_{1}}(-1,1,2,-2) \) in the 4-dimensional matrix.

The following passage will prove that the original definition of matrix rotation for any 3-dimensional \( {A_{i}} \) are still applicable on 4-dimensional matrix A.

The t rotational transformation, rotating a 2-dimensional matrix (like the kth layer of matrix \( {A_{i}} \) ) for t times, marked as \( R{o^{*}}(k,t) \) , can be expressed as follows: left-multiply the plane coordinates \( (i,j) \) of all the elements \( {A_{i}}(i,j,k) \) of the kth layer by the rotate matrix \( Rotat{e^{*}}(t) \) :

\( Rotat{e^{*}}(t)=[\begin{matrix}cos⁡tπ/2 & -sin⁡tπ/2 \\ sin⁡tπ/2 & cos⁡tπ/2 \\ \end{matrix}] \) (11)

This transformation still works for any 2-dimensional matrix component in a 4-dimensional matrix:

\( Ro(k,l,t):A(i,j,k,l)↦A(icos⁡\frac{tπ}{2}-jsin⁡\frac{tπ}{2},isin⁡\frac{tπ}{2}+jcos⁡\frac{tπ}{2},k,l) \) (12)

It is worth to notice that there are 2 dimensions orthogonal to the rotated plane in the 4-dimensional space, i.e., the rotary shaft in the 4-dimensional space is 2-dimensional, so at least 2 direction parameters are required to determine the rotary shaft for one rotation, and thus the rotational transformation requires 2 positional parameters in each direction to determine the rotated plane, and an integer parameter to determine the time of rotation.

In addition, rotations with a 4th dimension are not included in the rotation transformations in 3D space (e.g., \( Ro(i,k,t) \) , which does not exist as a mapping in 3D space), but can be constructed according to the above method. In fact, from the above statement "the rotary shaft has 2 dimensions", it can be determined that there are a totally \( C_{2}^{4}=6 \) rotary shaft directions in 4-dimensional space [2].

3.2. Proof of feasibility of expressing rotated (encrypted) sequences via multiple quaternion array

It is known that a rotation in one axis can be represented in three dimensions by a single quaternion. Similarly, rotation in four dimensions needs to be limited to two axes, and rotation for a single layer needs to be limited to the coordinates of that layer in both axes, otherwise the entire 4-dimensional matrix would be rotated. Here 4 orthogonal unit quaternions are needed to represent the directions, so a new axis l is added; accordingly, the constants used to represent the isometric scaling are not necessary. A more complete definition of the rotation transformation \( Rotate(d1,d2,h1,h2,t) \) is given here.

Let \( d1,d2 \) be the two axial directions, \( h1,h2 \) be the coordinates of the plane in the axial directions, and t be the number of rotations. With i,j,k,l representing the four directions, the plane generated by the two directions orthogonal to both \( d1 \) and \( d2 \) is rotated. At this point the forward direction of the rotation should be considered: the rotation by quaternions should satisfy: \( d{1^{*}}d2=-d{2^{*}}d1(d1≠d2) \) , which defines the sequentiality of the sequence \( i→j→k→i \) and maps the inverse order multiplication to be the reverse result [3-4]. It is also considered to continue following this definition in the 4-dimensional case: Firstly, construct a structure in 3-dimensional space, each vertex means one sign of i,j,k,l, then with the spacial relationship of this structure, the mapping order of quaternion arrays can be defined:

Figure 2: Schematic diagram of the correspondence between axial direction and rotation direction

As in Fig. 2, Rotate(i,j) is the rotation in the axial direction of (i,j), while (k,l) is the order of the rotation direction. Rotate(i,j) maps the coordinates of the original (k,l) plane to the new coordinates by left-multiplicating the rotation matrix to the vector \( {({h_{k}},{h_{l}})^{T}} \) , while the coordinates of the axial direction in the plane of (i,j) remains unchanged. Where \( ({h_{k}},{h_{l}}) \) is the original coordinates of (k,l) , i.e. the nodes on the rotating plane. The following mapping relations (see Table 1) are established with this order rule:

Table 1: Correspondence between the axial direction (left) and the rotational direction (right) of the Rotate function.

A rotation in four dimensions can then be uniquely expressed with two ordered axes and a rotating angle parameter. Since the rotation that will be discussed later is a rotation of a hypercube layer (with two dimensions), it is necessary to specify the coordinates of the two axes to determine the plane in which the object of rotation is located, named as h1 and h2. The function \( Rotate(d1,d2,h1,h2,t) \) can be used to represent the axes of d1 and d2, and the plane consisting of the nodes with coordinates h1 in the direction of d1 and h2 in the direction of d2 can be rotated by t*90^o in the order of the corresponding directions (with d1,d2 as the axis). This rotational transformation acts on the corresponding nodes, and the coordinates of the mapped nodes still form a 4-dimensional hypercube.

3.3. Feasibility proof of applying rotations determined by quaternion array to the SubBytes encryption

In order to apply the 4-dimensional cubic rotation method defined above to cryptography, it is necessary to ensure that the transform is a bijection, which means, there is no loss of information in the matrix after the rotation. The fact that 4-dimensional rotation does not result in loss of information can be directly deduced by the fact that rotation on a single plane does not result in loss of information, since a 4-dimensional rotation essentially changes the byte state of only one planar component. Whereas plane rotations are invertible transformations, any rotation has a unique inverse mapping, which means that for any image of that mapping there exists a unique preimage, so the mapping does not lead to the overwriting of valid information. It is also known that any plane of the hypercube is centrosymmetric about the shaft of that plane, and a rotation with an angle of \( kπ/2,(k∈Z) \) must still fall on the original coordinates, which means the information before the rotation will not be lost even after the rotation of a single plane, thus proving it.

4. Add key model design ( methods for generating encryption based on keys)

4.1. Rotated Byte Encryption Model

In order to realize the encryption model described previously, the correspondence between bytes and spatial locations needs to be constructed. Compared to building the spatial structure, assigning coordinates to each byte can determine the rotation transformation more Intuitively, because the rotation matrix left-multiplication of the byte coordinates can achieve the purpose, and this can also avoid the problems encountered in the byte transformation, such as the overwriting of valid information.

4.2. Program implementation and analysis

Table 2: Rotation encryption effect

In order to observe the encryption effect, those data shown in Table 2 are the number of nodes whose corresponding coordinates are the same as the initial state through the algorithm after 16 random rotational transformations in each round , and the data obtained after 100 experiments are (the third row is the result after rounding)[5]. The reason why we do not choose to follow the time complexity and avalanche effect of encryption to measure the efficiency and security of this encryption method is that the object of study here is only one step transformation in the encryption process, not a complete encryption method, and a single-step encryption transformation can not be directly compared with a complete encryption method [6].

The number of unbroken bytes after encryption decreases rapidly in the earlier rounds, yet this change is no longer significant after 4 rounds. This is mainly due to a property of the model itself.

When an element with 4-dimensional coordinates is rotated, the range of new coordinates it will be mapped to is restricted, and elements whose coordinates have a class of features will still only be mapped to coordinates with the same features after any rotational encryption. In this way, those bytes can be roughly categorized into five sets of elements according to their coordinate features:

\( {D_{0}}:\lbrace x∣x=(k1,k2,k3,k4),|k1|+|k2|+|k3|+|k4|=4\rbrace \)

\( {D_{1}}:\lbrace x∣x=(k1,k2,k3,k4),|k1|+|k2|+|k3|+|k4|=5\rbrace \)

\( {D_{2}}:\lbrace x∣x=(k1,k2,k3,k4),|k1|+|k2|+|k3|+|k4|=6\rbrace \)

\( {D_{3}}:\lbrace x∣x=(k1,k2,k3,k4),|k1|+|k2|+|k3|+|k4|=7\rbrace \)

\( {D_{4}}:\lbrace x∣x=(k1,k2,k3,k4),|k1|+|k2|+|k3|+|k4|=8\rbrace \) (13)

The number of elements in each set can be easily derived from the previous hypercube legend:

\( card({D_{0}})=16,card({D_{1}})=64,card({D_{2}})=96,card({D_{3}})=64,card({D_{4}})=16 \)

The coordinates that belonged to \( {D_{i}} \) before the rotation will only fall into \( {D_{i}} \) after the rotation, which provides degree of predictability to the rotation transformation itself, and means that the degree of disruption after the rotation is limited.

4.3. Cryptographic improvement optimization and comparison

Therefore, we consider adding another transformation: Exchange, which exchanges all the coordinates of the bytes in two parallel different 2-dimensional layers. It can be easily concluded that the transformation is still reversible by the one-to-one correspondence of the coordinates themselves, and the transformation can disrupt the nodes belonging to different sets of \( {D_{0}},{D_{1}},{D_{2}},{D_{3}},{D_{4}} \) . The degree of encryption is further improved by randomly adding the swap transform to each round of encryption (See Table 3).

Table 3: Encryption effect after adding swapping (8 random transformations per round)

The data shown in Table 3 comes from the encryption effect after adding the exchange transformation, and only 8 random rotations or exchanges (after rounding the third row) were performed in each round in order for the data to significantly reflect the encryption ability of the model. It can be seen that by the above method can significantly improve the encryption efficiency, then a better model is obtained.

5. Conclusion

In this paper, based on the original AES encryption, the security of the Subbytes encryption link is analyzed, and a new encryption model is further designed and improved to optimize its encryption effect. The experimental results show that the optimized encryption results have higher unpredictability and security, and can provide better protection for encrypted objects. In this paper, the research didn’t show the effect of the complete optimized AES encryption and algorithmic time complexity change of the improved AES encryption obtained after replacing the original Subbytes link with the new encryption model. Also, the research didn’t analyze the avalanche effect by comparing the strength of the two. In the next research, there are still many improvements that can be made, such as replacing the Subbytes link with this encryption optimization model, making the complete encryption program obtained into a product, and analyzing the performance of its memory usage, arithmetic power consumption, and encryption security through the above methods.