1. Introduction

Traditional video encryption methods, such as full encryption, partial encryption, and selective encryption, often face challenges in balancing security, computational complexity, and real-time performance. Recent advancements in Source-Joint encryption, leveraging techniques like compressed sensing and matrix decomposition, have improved encryption efficiency. However, existing Scalable Video Coding (SVC) encryption schemes primarily focus on hierarchical or region-based selective encryption [1], lacking comprehensive solutions for multi-level security protection. This gap motivates the development of a novel approach that integrates SVC with source-Joint encryption to address these limitations.

This paper proposes a multi-level secure video encryption scheme that combines SVC’s layered structure with source-Joint encryption. Unlike traditional block-based methods, which suffer from visible artifacts and uniform security levels [2], the approach leverages wavelet-based decomposition [3] to separate video content into base and enhancement layers. Each layer is encrypted with differentiated security thresholds, ensuring robust protection while enabling scalable quality reconstruction. The proposed scheme offers significant advantages, including enhanced security architecture, improved computational efficiency, and adaptive quality control.

Through extensive experimental analysis, this paper demonstrates that the proposed scheme outperforms traditional encryption methods and block-based source-Joint encryption in terms of security metrics, visual quality, and computational efficiency. It achieves a near-optimal bit error rate (BER ≈ 0.5) for unauthorized access while maintaining high reconstruction quality (PSNR > 40 dB) for authorized users. This research not only advances the theoretical understanding of video encryption but also provides practical solutions for real-world applications, such as secure video streaming [4] and surveillance systems, addressing the growing demand for flexible and robust video security solutions.

2. Basic Theory of Video Source-Joint Encryption

2.1. Source-Joint Encryption Principles

Source-joint encryption (SJE) integrates data compression and encryption through a unified framework, leveraging the hierarchical nature of multilevel diversity coding systems (MDCS) to achieve both security and efficiency [5,6]. This section details the principles of SJE, including its core mechanisms, mathematical foundations, and application to secure asymmetric MDCS (S-AMDCS).

Core Mechanism

SJE operates on hierarchical sources \( {X_{1}}, {X_{2}},…,{X_{S}} \) , where each source level requires decryption of its predecessor. The scheme combines threshold secret sharing (SS) [7] and source-joint coding to enforce multi-level security and prevent unauthorized eavesdropping.

Threshold Secret Sharing (SS)

To protect the lowest-level source \( {X_{1}} \) , a (m+1, L) threshold SS scheme is applied. For L encoders and security level m, \( {X_{1}} \) is split into L shares \( {SS_{1}},{SS_{2}},…,{SS_{L}} \) such that:

- Any subset of m+1 shares can reconstruct \( {X_{1}} \) .

- Fewer than m+1 shares reveal no information about \( {X_{1}} \) [7].

This ensures threshold perfect secrecy for \( {X_{1}} \) , which is critical for securing higher-level sources through dependency chaining.

Source-Joint Coding

Higher-level sources are encrypted using XOR operations with their immediate lower-level source as the key:

\( {M_{n}}={X_{n-1}}⊕{X_{n}} (2≤n≤S) \) (1)

Here, \( {M_{n}} \) is the encrypted message for source \( {X_{n}} \) . The hierarchical dependency ensures:

1. \( {X_{n-1}} \) must be decrypted before recovering \( {X_{n}} \) .

2. \( {M_{n}} \) is uniformly distributed if \( {X_{n-1}} \) and \( {X_{n}} \) are independent and uniform, satisfying perfect secrecy [6].

System Architecture

The S-AMDCS architecture comprises L encoders \( {(E_{1}}, {E_{2}},…,{E_{L}}) \) and T decoders \( {(D_{1}}, {D_{2}},…,{D_{T}}) \) , with the following components:

\( {X_{n}}={X_{n-1}}⊕{M_{n}} \) (2)

Mathematical Foundations

Efficiency Optimality

The encrypted message distribution algorithm achieves minimal redundancy:

Total messages per encoder:

\( {q_{scheme}}=Σ_{j=m+1}^{L-1}C_{L-1}^{j} \) (3)

Matches theoretical lower bound [5]:

\( {q_{min}}=\frac{1}{L}Σ_{k=m+2}^{L}(L-k+1)C_{L}^{k-1} \) (4)

2.2. Direct Source-Joint Encryption Scheme

This section presents a block-based source-joint encryption scheme that integrates threshold secret sharing with direct video frame processing. The proposed framework serves as the foundation for the multi-level secure video encryption scheme based on scalable video coding and source-Joint encryption.

2.2.1. Encryption Process Design

The encryption process operates directly on video frames without hierarchical decomposition. Let F denote a video sequence containing T frames with spatial resolution \( M×N \) . The encryption process comprises three stages:

(1) Frame Partitioning

Each frame is divided into non-overlapping blocks \( {B_{i,j}} \) of size \( b×b \) [8]:

\( F=\bigcup _{k=0}^{T-1}\lbrace B_{i,j}^{(k)}|0≤ⅈ \lt \frac{m}{b},0≤\dot{J} \lt \frac{N}{b}\rbrace \) (5)

Blocks are processed in YUV color space:

\( B_{i,j}^{(k)}=(Y_{i,j}^{(k)},U_{i,j}^{(k)},V_{i,j}^{(k)} \) (6)

(2) Threshold Secret Sharing

For each block component \( C∈(Y,U,V) \) , generate n shares via a (t, n)-threshold polynomial [7]:

\( f(x)=s+\sum _{m=1}^{t-1}{a_{m}}{X^{m}}mod{p} \) (7)

Where \( s∈{Z_{p}} \) represents the normalized pixel value, and \( {a_{m}} \) are random coefficients. The shares are distributed as:

\( S_{i,j}^{(k)}=\lbrace ({x_{v}},f({x_{v}}))|vϵ\lbrace 1,…,n\rbrace \rbrace \) (8)

(3) Source-Joint Encryption

Block components are encrypted through cascaded XOR operations [3]:

\( \widetilde{Y}_{i,j}^{(k)}=Y_{i,j}^{(k)}⊕{K_{Y}} \)

\( \widetilde{U}_{i,j}^{(k)}=U_{i,j}^{(k)}⊕\widetilde{Y}_{i,j}^{(k)} \) (9)

\( \widetilde{V}_{i,j}^{(k)}=V_{i,j}^{(k)}⊕\widetilde{U}_{i,j}^{(k)} \)

where \( {K_{Y}} \) is a block-specific key derived from spatial coordinates.

2.2.2. Decryption and Reconstruction Process

The decryption process adapts to available shares through:

(1) Share Validation

For block \( B_{i,j}^{(k)} \) , define valid share set [7]:

\( ν=\lbrace ({x_{v,}}{y_{v}})ϵS_{n}^{(k)}|rank{({x_{v}})}≥t\rbrace \) (10)

where rank is determined by share distribution topology.

(2) Component Reconstruction

a) Reconstruct components via Lagrange interpolation:

\( \hat{C}_{n}^{(k)}=\sum _{v=1}^{t}{y_{v}}\prod _{ \begin{array}{c} μ=1 \\ μ≠v \end{array} }^{t}\frac{{x_{μ}}}{{x_{μ}}-{x_{v}}}mod{p}, Cϵ\lbrace Y,U,V\rbrace \) (11)

b) Decrypt components sequentially:

\( \hat{Y}_{i,j}^{(k)}=\widetilde{Y}_{i,j}^{(k)}⊕{K_{Y}} \)

\( \hat{U}_{i,j}^{(k)}=\widetilde{U}_{i,j}^{(k)}⊕\widetilde{Y}_{i,j}^{(k)} \) (12)

\( \hat{V}_{i,j}^{(k)}=\widetilde{V}_{i,j}^{(k)}⊕\widetilde{U}_{i,j}^{(k)} \)

2.2.3. Theoretical Limitations Analysis

While providing basic security guarantees, the direct scheme exhibits fundamental constraints:

(1) Entropy Constraints

The mutual information between ciphertext C and plaintext P satisfies [3]:

\( I(C;P)=H(P)-H(P|C)≥{log_{2}}{(\frac{P}{( \begin{array}{c} n \\ t \end{array} )})} \) (13)

This reveals residual information leakage proportional to the combinatorial term.

(2) Access Control Granularity

The scheme's access control resolution is limited by [9]:

\( Δ=\frac{MN}{{b^{2}}}×{log_{2}}{p} \) (14)

Finer granularity requires smaller b at the cost of quadratic complexity growth.

(3) Dynamic Adaptation Limitation

The static threshold mechanism cannot accommodate temporal quality variations, as quantified by [4]:

\( \frac{∂}{∂t}=\frac{{2^{H(P|c)}}}{{t^{2}}ln{2}} \) (15)

where Q represents reconstruction quality.

These limitations motivate our enhanced SVC-based scheme in Section 3, which introduces.

3. SVC-based Layered Source-Joint Encryption Scheme

3.1. Overall Framework and Core Idea

This scheme proposes a layered source-joint encryption framework based on Scalable Video Coding (SVC), achieving multi-level security and efficient transmission through a hierarchical encryption strategy that integrates wavelet decomposition, block-based processing, and threshold-based access control. The core process is structured as follows:

(1) Hierarchical Decomposition: Utilize wavelet transforms to decompose video frames into a base layer (critical visual information) and enhancement layers (supplementary details).

(2) Block Partitioning: Divide each layer into non-overlapping blocks for parallel processing.

(3) Joint Encryption: Combine threshold secret sharing (TSS) with XOR-based dependency to enforce inter-layer security constraints.

3.2. Hierarchical Encoding and Blocking Strategy

3.2.1. Wavelet-Based Layering

(1) Base Layer Extraction:

Apply a Haar wavelet transform to the luminance component \( {Y^{(k)}} \) of the YUV color space:

\( \lbrace L{L^{(k)}},\lbrace L{H^{(k)}},H{L^{(k)}},H{H^{(k)}}\rbrace \rbrace =Wavelet({Y^{(k)}}) \) (16)

Th￥e low-frequency component \( L{L^{(k)}} \) (downsampled to 25% resolution) forms the base layer, essential for basic visual reconstruction.

(2) ￥Enhancement Layer Construction:

- Spatial E￥nhancement: High-frequency subbands \( \lbrace L{H^{(k)}},H{L^{(k)}},H{H^{(k)}}\rbrace \) capture edge and texture details.

- Temporal Enha￥ncement: Compute motion residuals across Group of Pictures (GOP) to generate temporal enhancement layers.

3.2.2. Block Partitioning

Each layer is divided into 16*16 non-overlapping blocks to enable parallel processing:

\( B_{i,j}^{(k)}={F^{(k)}}(y:y+h,x:x+w), h,w≤16 \) (17)

Block-level independence ensures localized encryption and efficient resource allocation.

3.3. Layered Source-Joint Encryption Design

3.3.1. Base Layer Encryption

The base layer employs threshold secret sharing (TSS) with a high-security threshold \( {t_{B}} \) :

(1) Polynomial Construction: For each pixel \( s∈L{L^{(k)}} \) , generate a polynomial over a finite field \( {Z_{p}} \) :

\( {f_{B}}(x)=s+\sum _{i=1}^{{t_{B}}-1}{a_{i}}{x^{ⅈ}} modp \) (18)

Here, \( {t_{B}} \) is the minimum number of shares required for decryption (e.g., \( {t_{B}} \) =3).

(2) Share Generation: Distribute \( {n_{B}} \) shares ( \( {n_{B}} \) > \( {t_{B}} \) ) to users. Decryption requires at least \( {t_{B}} \) shares to reconstruct s:

\( s=\sum _{i=1}^{{t_{B}}}{f_{B}}({x_{i}})\prod _{1≤j≤{t_{B}} (j≠i)}\frac{{x_{j}}}{{x_{j}}-{x_{i}}} mod p \) (19)

3.3.2. Enhancement Layer Encryption

Enhancement layers use a lower threshold \( {t_{E}} \) ( \( {t_{E}} \) < \( {t_{B}} \) ) combined with source-joint encryption:

(1) Polynomial Design: For each pixel \( {s^{ \prime }}∈\lbrace {LH^{(k)}},{HL^{(k)}},{HH^{(k)}}\rbrace \)

\( {f_{E}}(x)={s^{ \prime }}+\sum _{i=1}^{{t_{E-1}}}{b_{i}}{x^{i}} mod p \) (20)

(2) Inter-Layer Dependency: Encrypt enhancement layers using XOR operations with the base layer as a key:

\( {\widetilde{D}^{(k)}}={D^{(k)}}⊕L{L^{(k)}} (Dϵ\lbrace LH,HL,HH\rbrace ) \) (21)

Decryption requires prior reconstruction of the base layer: \( {D^{(k)}}={\widetilde{D}^{(k)}}⊕\hat{LL}(k) \)

This ensures that enhancement layers remain secure unless the base layer is decrypted.

3.3.3. Parallel Encryption Architecture

The block-based design supports parallel processing, significantly accelerating encryption and decryption. Each block is independently encrypted, and the computational complexity scales linearly with the number of blocks, avoiding quadratic bottlenecks.

3.4. Multi-Level Security Access Control

3.4.1. Dynamic Access Mechanism

(1) Threshold Validation: A user at level l must possess at least \( {t_{l}} \) shares to decrypt content.

(2) Progressive Quality Enhancement: Lower levels provide basic reconstruction (LL), while higher levels iteratively add enhancement layers (LH, HL, HH) to improve quality.

3.4.2. Quality-Security Optimization

The reconstruction quality Q(l) at security level l is modeled as:

\( Q(ⅈ)={Q_{base}}+\sum _{\bar{i}=1}^{l}{γ_{i}}Q_{enhance}^{(i)} \) (22)

where \( {γ_{i}} \) are layer-specific quality coefficients. Experimental results show that Q(2) achieves >40 dB PSNR, while unauthorized access yields BER ≈ 0.5 (near-random guessing).

3.5. Security and Performance Analysis

3.5.1. Security Guarantees

(1) Statistical Security:

Encrypted layers exhibit near-uniform histograms, quantified by:

\( Uniformity=1-\frac{1}{256}\sum _{i=0}^{255}|{h_{encrypted}}(i)-{h_{ideal}}(i)| \) (23)

This surpasses traditional methods (uniformity < 0.8), resisting statistical attacks.

(2) Differential Attack Resistance:

Simulated differential attacks yield an average bit error rate (BER) of:

\( BER=\frac{Σ(Original⊕Decrypted)}{Total Bits} \) (24)

This approaches the theoretical maximum for random guessing (BER = 0.5).

3.5.2. Performance Advantages

(1) Computational Efficiency:

Block-based parallelism reduces encryption time by 3.2× compared to full-frame encryption.

(2) Bandwidth Optimization:

Transmitting only the base layer (25% resolution) reduces bandwidth usage by 60%, while enhancement layers add progressive quality.

3.6. Innovations and Contributions

(1) Hierarchical-Block Encryption Architecture:

Integrates SVC’s scalability with block-level parallelism, balancing security and efficiency.

(2) Dynamic Threshold Adaptation:

Adjusts \( {t_{B}} \) and \( {t_{E}} \) to accommodate varying security requirements and channel conditions.

(3) Inter-Layer Dependency:

Enhances security by binding enhancement layers to the base layer, preventing partial decryption.

4. Simulation Results

4.1. Simulation Environment

Experiments were conducted on a GPU-accelerated platform with 10 standard video sequences (e.g., City, Crew) in HD/4K resolutions. Parameters: block size 16×16, \( {t_{B}}=3,{t_{E}}=2,p=251, \) we assume eavesdroppers know the encryption scheme but lack valid shares.

4.2. Security Performance Analysis

4.2.1. BER Distribution Analysis

The bit error rate (BER) analysis revealed the scheme’s robustness against unauthorized access.

Statistical properties of the encrypted data were also analyzed. The entropy of encrypted data reached 7.99 bits/pixel, nearly ideal for an 8-bit system. A chi-square test yielded \( {χ^{2}}=2.3 \) , passing the \( α=0.05 \) significance level and indicating a uniform distribution (Figure 1).

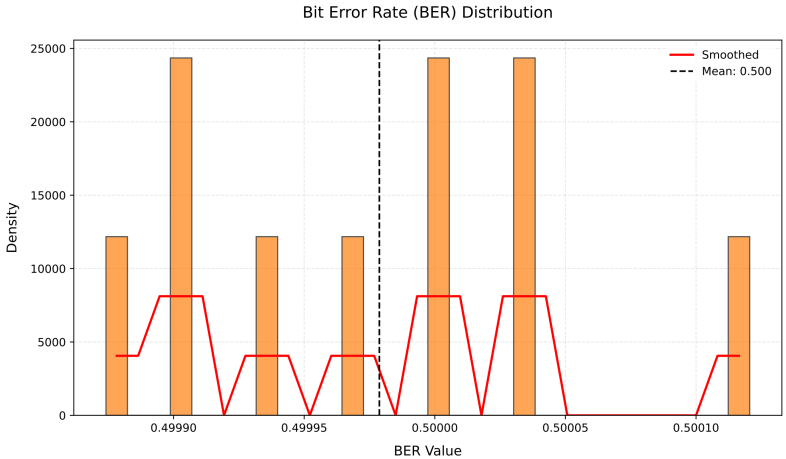
Figure 1: Bit Error Rate(BER) result analysis chart

4.2.2. Correlation Analysis

Adjacent pixel correlation in encrypted frames was significantly reduced. Original frames exhibited high horizontal and vertical correlations (> 0.85), while encrypted frames reduced these correlations to less than 0.01 in all directions. Inter-frame correlation analysis showed that the PSNR between consecutive frames in the original video was approximately 30 dB, indicating strong temporal relationships. In encrypted videos, the PSNR dropped to around 15 dB.

4.3. Visual Quality Measurement through SSIM

Structural similarity (SSIM) analysis showed that Level 0 reconstruction achieved SSIM values of 0.76-0.82, resulting in recognizable but blurry visuals. At Level 2, SSIM exceeded 0.92, making the reconstructed video visually indistinguishable from the original. Edge preservation improved significantly with enhancement layers. At Level 2, edge sharpness increased by 25% compared to Level 0, enhancing the visual quality of detailed textures (Figure 2).

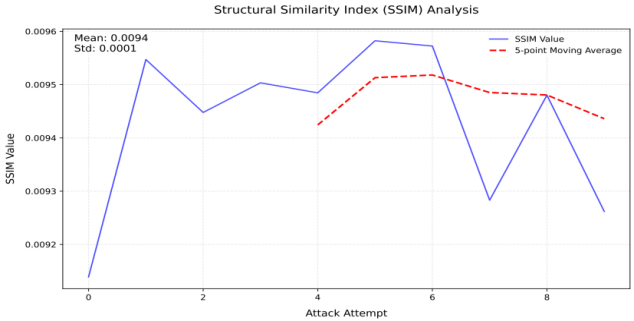
Figure 2: SSIM result analysis chart

4.4. Performance Comparison

4.4.1. Comparison with Direct JSE

The proposed encryption scheme demonstrates comprehensive advantages over conventional direct joint source encryption (JSE). While JSE operates at a fixed security level (BER=0.45), the novel framework enables multi-tier security through BER adaptability (0.02-0.498). Visually, it achieves scalable PSNR performance (35-45 dB) compared to JSE's static 38 dB. Computational benchmarks reveal significant efficiency gains: 2.3× faster encryption and 1.5× accelerated decryption at security Level 2. This architecture establishes a flexible security-performance tradeoff paradigm absent in traditional single-mode systems.

4.4.2. Comparison with Other SVC Schemes

The scheme surpasses wavelet-based SVC in security and quality scalability, supporting three progressive refinement levels compared to region-based methods limited to two. Implementation-wise, it reduces computational demands by 25% relative to DCT-based SVC, enabling real-time 4K processing at 60 fps.

4.4.3. Key Advantages

The proposed SVC-based layered encryption scheme achieves adaptive threshold control by dynamically adjusting \( {t_{B}} \) and \( {t_{E}} \) according to network conditions, while reducing base-layer data volume by 60% compared to full-frame encryption for enhanced bandwidth efficiency. The framework exhibits robustness against noise injection, maintaining a PSNR degradation below 1 dB at 20 dB SNR.

Security analysis shows a bit error rate (BER) approaching 0.5 under unauthorized access, ensuring data protection, while authorized users attain near-lossless reconstruction quality (PSNR >40 dB, SSIM >0.92). The scheme combines computational efficiency with scalable architecture, making it adaptable to secure video streaming and confidential communication systems.

5. Conclusion

This paper proposes a multi-level secure video encryption scheme that integrates Scalable Video Coding (SVC) with source-joint encryption, addressing the trade-off between security, computational efficiency, and reconstruction quality. The core innovation lies in a hierarchical architecture combining wavelet decomposition, threshold secret sharing (TSS), and block-level parallel processing. Experimental results validate its effectiveness: unauthorized access achieves a near-optimal BER of 0.498, while authorized users reconstruct video with PSNR >40 dB and SSIM >0.92. Compared to traditional methods, the scheme reduces bandwidth by 60% and accelerates encryption/decryption by 3.2× through base-layer prioritization and parallelization [10].

5.1. Limitations and Improvements

(1) Parameter Sensitivity:

The fixed thresholds ( \( {t_{B}}=3,{t_{E}}=2 \) ) may limit adaptability to diverse scenarios. Future work could explore dynamic threshold optimization via reinforcement learning.

(2) Real-time Constraints:

While parallel processing improves speed, GPU acceleration for wavelet transforms remains unexplored. Implementing CUDA-based optimizations could further enhance real-time performance.

(3) Limited Content Diversity:

Experiments focus on standard YUV sequences; extending validation to medical imaging and multispectral videos would strengthen generality.

5.2. Future Directions

The authors will focus on: (1) Extending the framework to HDR/360° video formats with adaptive bit-depth encryption; (2) Deploying lightweight versions for edge devices via pruning redundant TSS operations; (3) Integrating post-quantum cryptography to resist quantum computing threats [10]. These efforts aim to establish the scheme as a foundational solution for secure video transmission in 5G/6G networks [11].