1.Introduction

1.1.Background

Cosmic rays are high-energy particles from outer space, mainly protons and a smaller number of heavy nuclei. Upon entering Earth’s atmosphere, these particles interact with atmospheric molecules, producing secondary particles such as muons. As byproducts of cosmic rays, muons are abundant in the atmosphere and can penetrate the atmosphere to the Earth’s surface, making them essential for studying cosmic ray properties.

1.2.Research motivation

Understanding the relationship between atmospheric pressure and muon detection rates is crucial for improving our knowledge of cosmic ray transmission and attenuation. Since atmospheric pressure affects the number of muons that reach the Earth’s surface, it is important for accurate data analysis and detector calibration under various environmental conditions. Additionally, detecting “coincidence events” with multiple detectors can reveal rare cosmic ray phenomena, such as high-energy particle bursts or particle streams from solar storms.

1.3.Literature review

Extensive research has been conducted on muon production, movement, and decay mechanisms. Abbasi et al. [1] examined the influence of barometric pressure on the detection rate of mesons and discovered that the greater the pressure, the fewer the number of mesons reaching the Earth's surface, as the increased air density leads to enhanced absorption and attenuation of mesons. Comparably, the experiments conducted by Patrick et al. [2] at different altitudes also uphold this conclusion. Axani et al. [3] introduced a portable detector that can be used to measure the flux of cosmic rays. Lecoq [4] presented the most widely utilized detection methods currently employed in particle physics experiments, namely charged particle detectors and photon scintillation detectors. Maghrabi et al. [5] studied how the physical environment of low latitude observatories, such as atmospheric pressure, temperature, humidity, etc., affects cosmic ray muons. This study’s innovation lies in its use of data from multiple Cosmic Watch detectors to achieve more accurate time synchronization and event identification, thereby improving our understanding and precision in detecting cosmic ray events.

1.4.Research questions

This study primarily addresses the following questions:

1) How does atmospheric pressure variation affect muon detection rates?

2) How can time discrepancies between detectors be corrected to detect multiple coincidence events accurately?

1.5.Research objectives

This study aims to understand how atmospheric pressure influences muon detection rates by analyzing data from Cosmic Watch detectors. Additionally, it seeks to create a method for identifying coincidence events through time correction, thereby increasing the precision and reliability of detector performance under different conditions.

2.Methods

2.1.Data collection

Data were collected from six Cosmic Watch detectors, each recording events over different time periods. The datasets include timestamps (measured in milliseconds relative to detector activation), atmospheric pressure (in Pascals), and event flags (e.g., coincident == 1).

2.2.Data grouping

The crux of data grouping lies in ensuring that the data files from different detectors are recorded within an identical time period to enable precise comparison and analysis. Firstly, a relationship graph of pressure versus timestamp is generated for each data file, and these graphs can act as "fingerprints" to represent the recording time of the data. Subsequently, by comparing the similarity of these graphs, the files within the same time period are categorized into one group.

This procedure is executed utilizing the K-Means clustering algorithm.

\( Distance Measure=\sqrt[]{\sum _{i=1}^{n}{({p_{i1}}-{p_{i2}})^{2}}} \)

2.3.Muon detection rate calculation

In order to calculate the meson detection rate for each data file, we pay particular attention to the coincident events (coincident == 1):

(1). Screening the coincident events: Select the events that fulfill the conditions to generate a new dataset.

(2). Computing the event count N: Calculate the number of coincident events.

(3). Calculating the total time T: Use the timestamp data to compute the total time span of the recorded data.

\( T=max{(Timestampe)}-min⁡(Timestamp) \)

(4). Computing the event rate R:

\( R=\frac{N}{T} \)

2.4.Pressure and detection rate analysis

For the analysis of the influence of atmospheric pressure on the event rate, we modeled the relationship between the event rate and the atmospheric pressure as a linear one. Firstly, the pressure difference Δp = Pressure - 101325 (relative to the standard atmospheric pressure) was calculated for each data file. Subsequently, a linear regression analysis via the least squares method was conducted to fit the relationship between the event rate R and the pressure difference Δp:

\( R = a · Δp + b \)

The regression coefficient a indicates the effect of pressure variation on the event rate, while the intercept b represents the baseline event rate.

2.5.Time difference analysis and correction

To ensure that the time stamps of the detectors are synchronized, we calculated the time difference (Δt) between each pair of detectors. The specific steps are as follows:

(1). Calculate the time difference: For each event of the detectors, calculate the time difference\( Δt ={ ts_{T}} - {ts_{B}}. \)

(2). Filter the time difference data: To ensure the accuracy of the analysis, only retain data with an absolute time difference within 2000 ms.

To correct these time differences, we used a linear fitting method to determine the time offset:

\( Δt = a · t + b \)

3.Results

3.1.Muon detection rate analysis

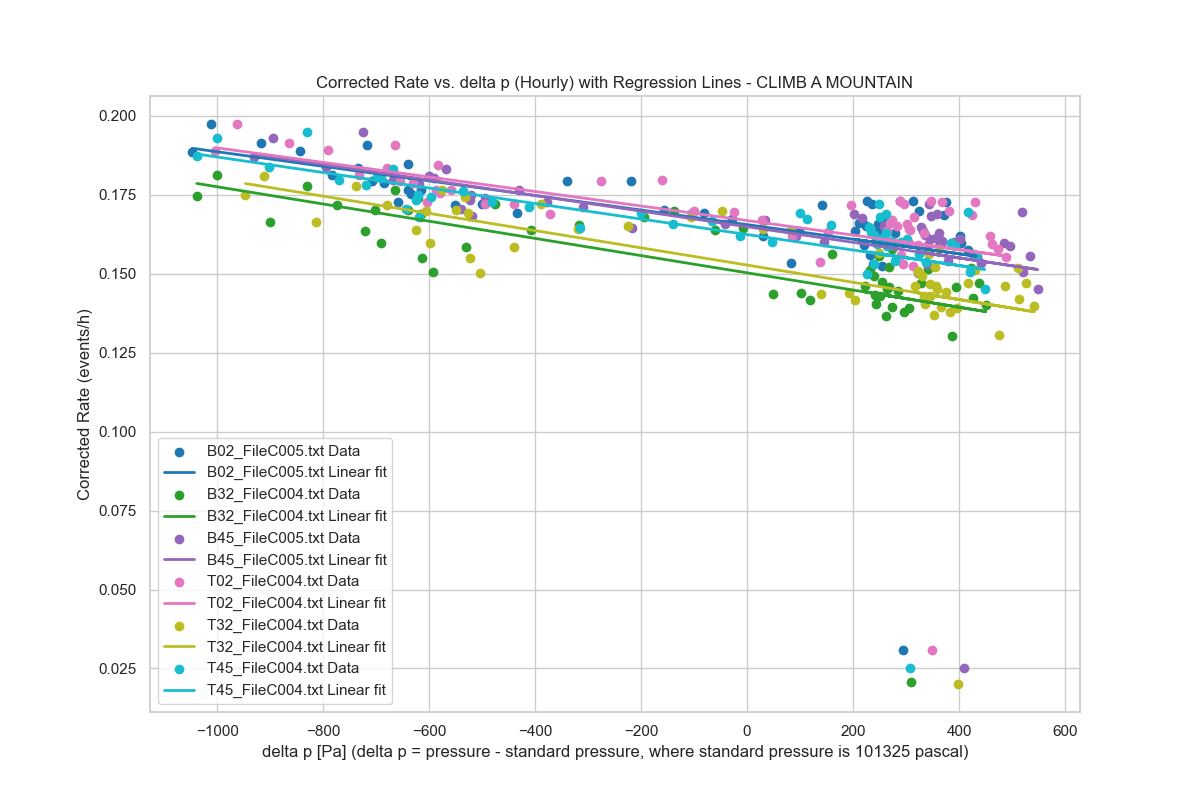
Figure 1: Our analysis shows a clear negative correlation between atmospheric pressure and muon detection rates, meaning that higher pressure is linked to fewer detected muons. This result aligns with existing literature in the field

3.2.Refining histogram analysis

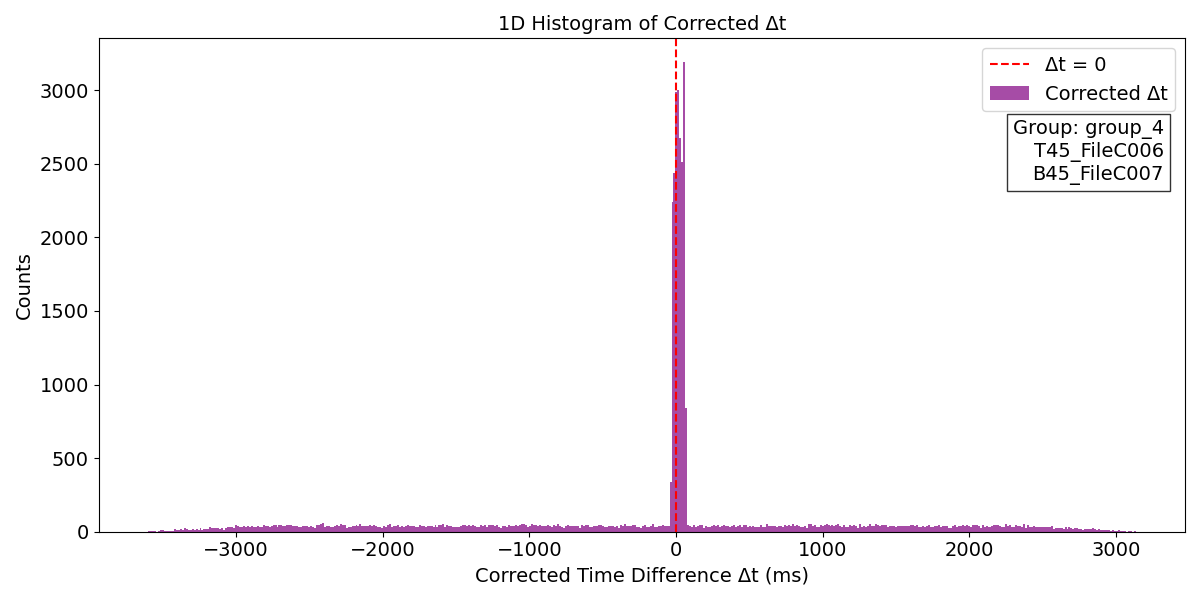
Figure 2: A refined histogram analysis was conducted to enhance peak localization and accuracy using a narrower bin width. By distributing peaks over at least three to five bins, the precise determination of peak position, width, and shape was achieved while reducing the influence of background noise. This arrangement markedly improved the resolution and accuracy of the data analysis

3.3.Time synchronization and correction

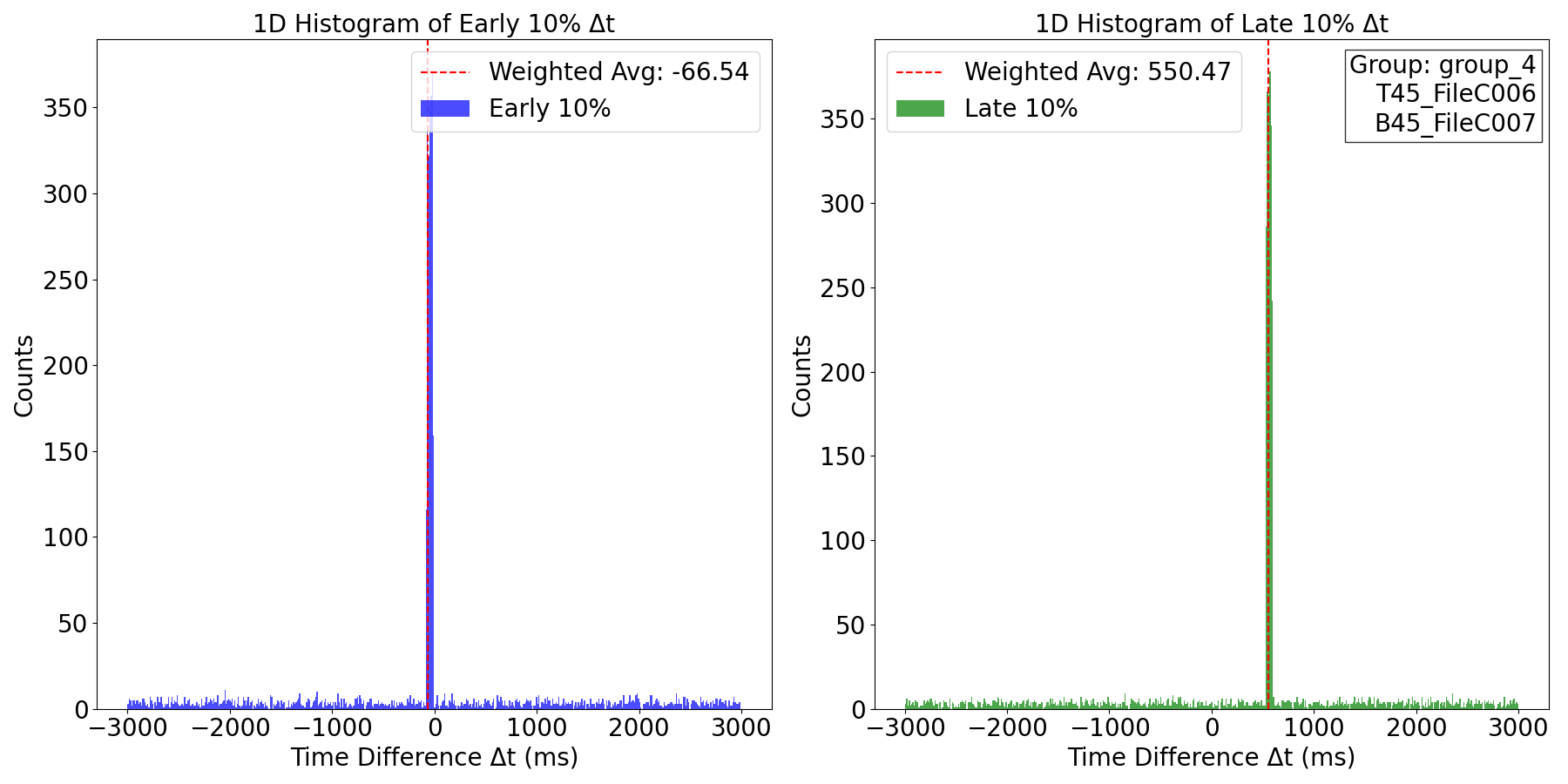
Figure 3: Initial time difference corrections led to the generation of adjusted time difference plots, followed by iterative optimization. Each correction round included saving computed time differences and timing data, facilitating faster processing in subsequent iterations. This iterative refinement significantly enhanced time synchronization accuracy among different detectors, laying a more reliable basis for future identification of coincidence events

3.4.Improvements in data grouping and analysis methods

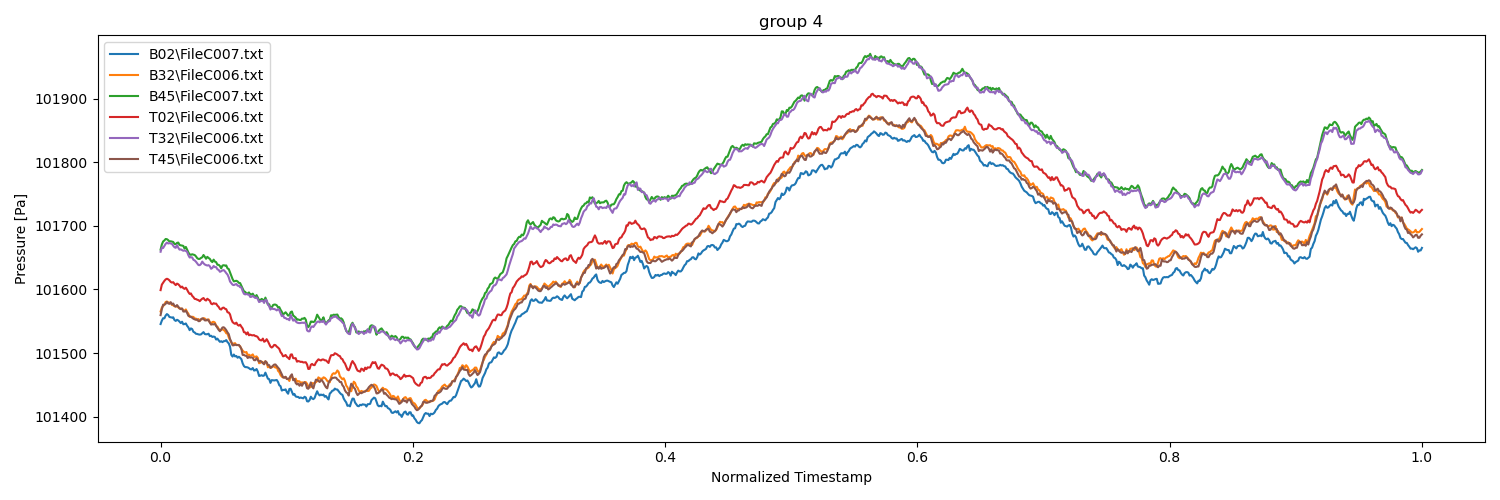
Figure 4: In the results, further elaboration was provided on how to group the data by employing the images of pressure and timestamps. These images were utilized as "fingerprints" to assist in identifying which files were recorded concurrently and ensure the accuracy of data grouping

3.5.Identification and correction of anomalous data

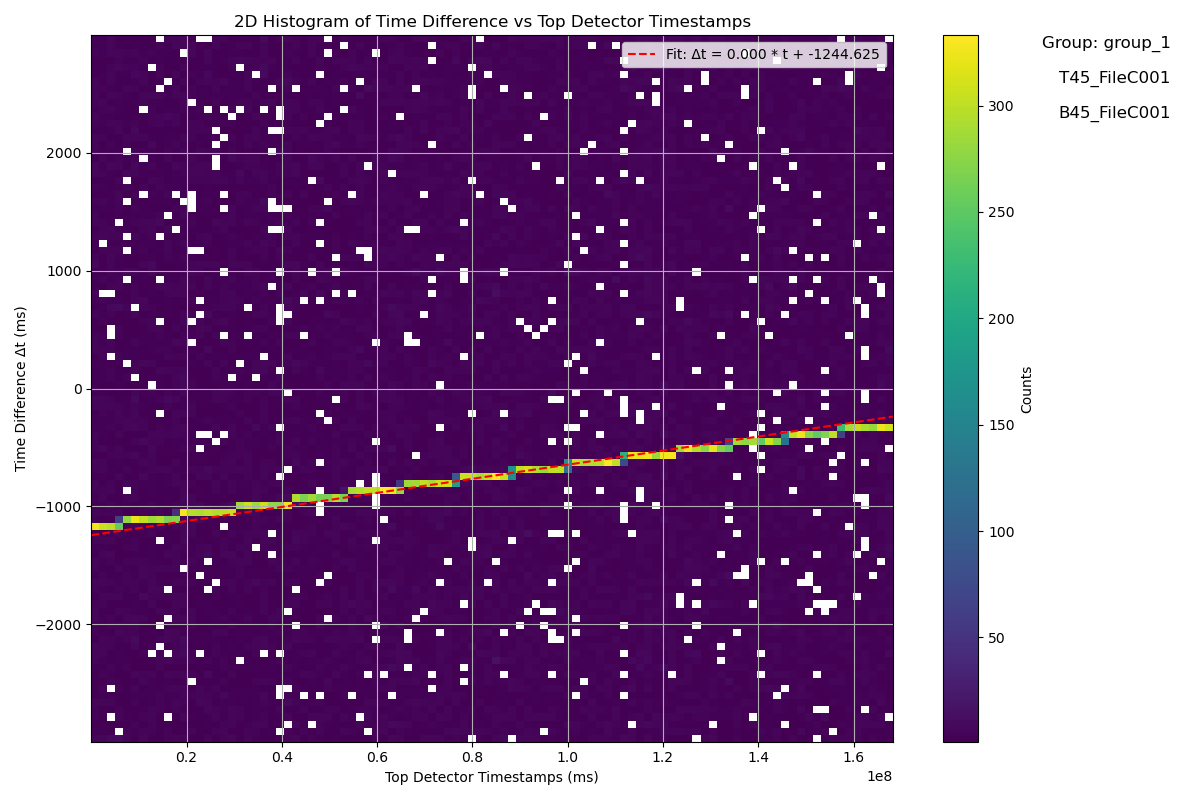
Figure 5: During the time difference correction process, we identified anomalies in the data and gradually narrowed the correction scope to refine the correction outcomes. The initial correction estimates might have contained errors; therefore, by repeatedly iterating and optimizing the correction function, the precision of the detector time synchronization and the detection capability of coincidence events were enhanced

4.Discussion

4.1.Interpretation of results

The research outcomes demonstrate a negative correlation between the meson detection rate and the atmospheric pressure, which is in accordance with the physical principle that the increase in atmospheric density leads to an elevated meson attenuation rate. Simultaneously, the time difference correction has significantly enhanced the detection accuracy of coincidence events, offering substantial support for the detection of rare cosmic ray events in multi-detector settings in the future.

4.2.Comparison with other studies

The outcomes of this research are in line with previous studies, yet provide an innovation in the temporal synchronization correction approach. The linear fitting and correction method employed in our study has manifested higher precision and reliability in the data analysis of multiple detectors, which is hitherto unprecedented in the existing literature.

4.3.Limitations of the study

The limitations of this research encompass the potential problems of data quality, such as file corruption or recording errors. Furthermore, this study assumes that atmospheric pressure is the sole environmental factor influencing the muon detection rate, while other possible variables, like temperature and humidity, were not taken into account.

4.4.Future research suggestions

Future studies could further refine time synchronization methods and explore how muons behave under various atmospheric conditions. Including a wider range of detectors in research could also help validate these findings.

5.Conclusion

Through analysis of Cosmic Watch detector data, this study has identified a negative correlation between atmospheric pressure and muon detection rates, making refinement of the time synchronization methods. These advancements offer new strategies and tools for detecting rare coincidence events captured by multiple detectors, contributing valuable insights to cosmic ray research and enhancing our understanding and prediction of high-energy particle events.

Statement of work

This research is the outcome of the collective efforts of the team members. Xuanzhu An, as the primary developer, was accountable for composing the core computing code, organizing the data, visualizing the data, and undertaking the majority of the analysis work. Additionally, she wrote the abstract, introduction, and the majority of the methods section of the paper. Haotian Yao assisted with data visualization, calculated the corrected event rate, and authored the discussion section. Haoran Yao was in charge of optimizing and modifying the code, computing the meson event rate, and penning the analysis and results section of the paper. All authors participated in the review process of the paper and unanimously consented to the final version.

Acknowledgments

We would like to convey our profound appreciation to Professor Gunther Roland, whose professional knowledge and selfless support have been of paramount significance for our academic advancement. Simultaneously, we offer our sincere gratitude to teaching assistants Jialong Guo and Xingyu Yi for their invaluable suggestions regarding technical minutiae and paper composition. We are also indebted to Liu Jiayi for participating in certain research discussions, as well as all anonymous researchers for providing clear and significant data from cosmic observatory detectors. Furthermore, we express our gratitude to the CIS organization for its summer camp and Shanghai Jiao Tong University for providing the venue, which laid the foundation for the success of our collaboration and research. All the authors contributed equally to this work and should be considered as co-first author.