1. Introduction

The study of elliptic flow in high-energy heavy-ion collisions, such as Pb+Pb collisions, is essential for understanding the properties of the quark-gluon plasma (QGP), a state of matter believed to exist shortly after the Big Bang. One of the key observables in these collisions is the elliptic flow, characterized by one-half of the second Fourier coefficient of the \( ∆ϕ \) distribution \( {v_{2}} \) , which provides insights into the initial geometry and the subsequent hydrodynamic expansion of the QGP.

Previous studies have shown that the Fourier coefficients of the \( ∆ϕ \) distribution are sensitive to the initial geometry of the collision and the subsequent hydrodynamic evolution of the system. For instance, Alver and Roland (2010) discussed the role of collision-geometry fluctuations in generating triangular flow, quantified by the third Fourier coefficient \( { v_{3}} \) [2]. Their findings highlighted the importance of understanding both \( {v_{2}} \) and \( {v_{3}} \) to gain a comprehensive picture of the QGP dynamics. Hence, the studying of advanced algorithms on prediction of the initial geometry of heavy-ion collisions is essential for research of the QGP dynamics.

One of the models that has been widely used to describe the initial geometry is The Glauber model. This model pro- vides a framework for calculating quantities such as the number of participant nucleons (N_part) and the number of binary collisions (N_coll), which are crucial for interpreting flow measurements. Miller et al. (2007) reviewed the application of the Glauber model in high-energy nuclear collisions and emphasized its relevance for flow studies [1].

In addition to the Glauber model, the A Multi-Phase Transport (AMPT) model also plays a significant role in understanding the dynamics of heavy-ion collisions. The AMPT model incorporates both the initial partonic and the hadronic phases, allowing for a comprehensive simulation of the collision process. Lin et al. (2005) demonstrated the effectiveness of the AMPT model in addressing the non-equilibrium effects experienced by particles with high transverse momentum (p_T) [3]. This model provides valuable insights into the development of hydrodynamics flow and the interactions within the QGP. With the prediction of those two models, the real data collected from Pb+Pb collisions are analyzed and compared.

Our study aims to analyze the elliptic and triangular flow in Pb+Pb collisions using data collected by the sPHENIX detector. By examining the ∆ϕ distribution, v₂ (p_T), and v₃ (p_T), we aim to gain a deeper understanding of the hydrodynamic properties of the QGP. The results from our experimental data are compared with predictions from the PHOBOS Glauber Monte Carlo model and the AMPT model, providing a comprehensive overview of the flow dynamics in these collisions.

2. Analysis of azimuthal correlations

The sPHENIX detector, located at the Relativistic Heavy Ion Collider (RHIC), offers high precision data of Pb+Pb collisions to study. This dataset includes measurements of the transverse momentum (p_T), pseudorapidity (η), and azimuthal angle (ϕ) of particles produced in Pb+Pb collisions.

2.1. Raw data

The initial step of our analysis involved processing the raw data obtained from the sPHENIX detector. Those fundamental quantities are essential for understanding the behavior of particles under the extreme conditions created in heavy-ion collisions.

We visualized the distributions of these variables to gain initial insights into the data. Figure 1 presents the histograms of p_T , η, and ϕ, respectively.

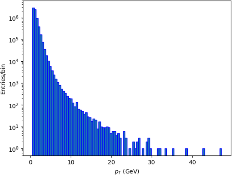
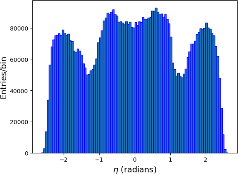
(a) pT distribution (b) η distribution (c) azimuthal angle

Figure 1: Distributions of p_T , η, and ϕ

The p_T distribution, shown in Figure 1. (a), expresses a characteristic inverse power-law shape, which is typical for heavy-ion collisions. This distribution indicates that many particles are produced with low p_T , while only a few gains high p_T .

The η distribution in Figure 1. (b) demonstrates the spread of particles along the beam axis, which are expected to be approximately symmetric around η = 0. This symmetry reflects the balanced nature of the collisions, where particles spread evenly in both directions relative to the central collisions point.

Lastly, depicted in Figure 1. (c), the ϕ distribution exhibits the angular spread of particles in the transverse plane. The valleys in the distribution can be attributed to the non-uniform acceptance and efficiency of the detector.

2.2. 1-Dimensional correlation function of ∆ϕ

In order to explore the azimuthal correlations of particles produced in the Pb+Pb collisions, we analyzed the ∆ϕ distributions for same-event pairs and mixed-event pairs. The ∆ϕ distribution exhibits the differences in the azimuthal angle ϕ between pairs of particles.

Figure 2 shows the ∆ϕ distributions for same-event pairs and mixed-event pairs. The same-event ∆ϕ distribution exhibits a pronounced peak around ∆ϕ = 0, indicating a strong azimuthal correlation among particles produced in the same collision event. This peak suggests that particles are preferentially emitted close to each other in azimuthal angle, reflecting the hydrodynamic flow within the QGP

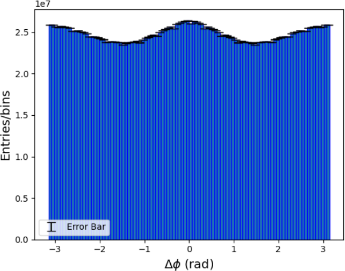
(a) ∆ϕ distribution of same- event pairs (b) background ∆ϕ distribution of mixed-event pairs.

Figure 2: ∆ϕ distribution of same-event pairs and mixed- event pairs

On the other hand, the mixed-event ∆ϕ distribution, which serves as a background reference, shows a much flatter distribution without a pronounced peak. Mixed- event pairs are constructed by combining particles from different events, which is typically used for reducing back- ground noise and correcting for acceptance effects. A method similar to that mentioned in [4] was applied to investigate the elliptic flow, which is using the correlation function. The background-subtracted correlation function is given by:

\( C(Δϕ)=\frac{S(Δϕ)}{B(Δϕ)} \) (1)

where S(∆ϕ) is the same-event distribution and B(∆ϕ) is the mixed-event distribution. By using this equation, we normalize the same-event distribution by the mixed- event distribution to form the correlation function, which corrects non-physical correlations and acceptance effects.

2.3. Fitting function of ∆ϕ correlation function

To quantify the azimuthal correlations observed in previous analysis, we fit the ∆ϕ distribution to a Fourier series. The Fourier decomposition allows us to extract the flow coefficients, which characterize the strength of azimuthal anisotropies in particle emission. Specifically, we focus on the second and third Fourier coefficients, corresponding to elliptic and triangular flow, respectively.

The Fourier series used for fitting the ∆ϕ Distribution is given by: \( \)

\( f(ϕ)=k(1+2v_{2}^{2}cos{(2ϕ)}+2v_{3}^{2}cos{(3ϕ)}) \) (2)

where v₂ and v₃ represent the magnitudes of elliptic and triangular flow, and k is a normalization factor.

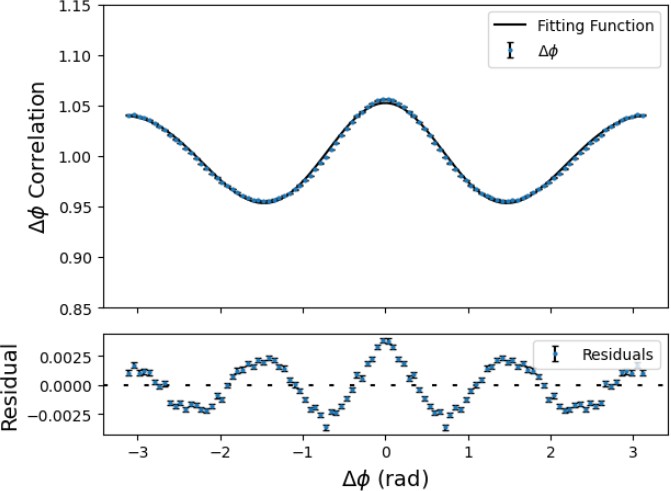
Figure 3: Fitting function and fitting residual of ∆ϕ correlation function

Figure 3 shows the fitted function to the ∆ϕ distribution and the corresponding residuals. The fitted function captures the main features of the ∆ϕ distribution, with the v₂ and v₃ coefficients providing a measure of the strength of the elliptic and triangular flow. The periodic pattern of fitting residual indicates that higher orders of hydrodynamic flow also exist in heavy ion collisions, though their contribution is relatively small compared to v₂ and v₃. However, it is a reasonable approximation to only consider the elliptic flow and triangular flow as the residual has a negligible magnitude.

2.4. 2-Dimensional correlation function of ∆ϕ and ∆η

To further investigate the azimuthal and longitudinal correlations between particles, we constructed the 2- dimensional correlation function of ∆ϕ and ∆η. The ∆ϕ represents the azimuthal angle difference between particle pairs, while ∆η denotes the pseudorapidity difference.

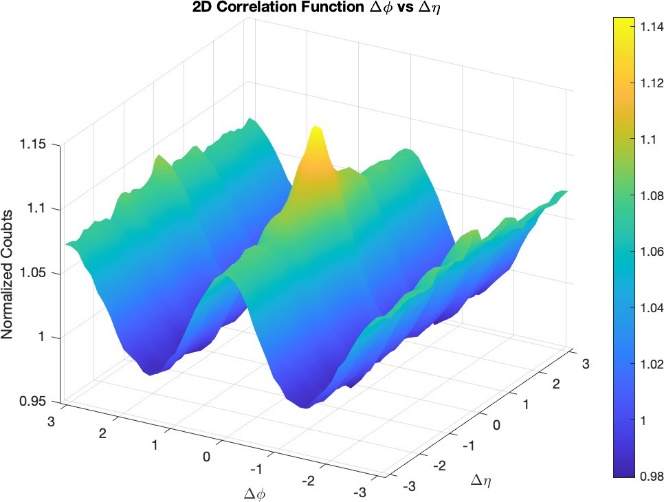
Figure 4: 2D correlation function of ∆ϕ and ∆η

In Figure 4, the noteworthy peak at the origin points indcates a strong correlation among particles emitted close to each other in both azimuthal angle and pseudorapidity. This peak is a signature of collective flow in the QGP, where particles exhibit collective behavior due to the high energy density and strong interactions within the plasma. In addition, the narrow peak in ∆η suggests that particles are emitted over a short range in pseudo- rapidity.

2.5. Excluding collision pairs with \( |Δη| \lt 1 \)

After plotting the 2-dimensional and 3-dimensional \( ∆η \) versus \( ∆ϕ \) correlation functions, it can be observed that the peak at (0,0) is contributed by both the trigonometric shape of \( ∆ϕ \) distribution and the triangular shape of \( ∆η \) .

Table 1: Fit parameters \( {v_{2}} \) and \( {v_{3}} \) for the whole dataset and the filtered dataset

Therefore, collision pairs with \( |Δη| \lt 1 \) should be ex- cluded since they are unrelated to hydrodynamic expansion. The \( ∆ϕ \) correlation function, its fitting function, and the fitting residual for collision pairs with \( |Δη| \lt 1 \) are shown in Fig. 5.

Figure 5: Fitting function and fitting residual of \( ∆ϕ \) corre-lation function excluding pairs with |Δη|<1

After excluding pairs that are irrelevant to the hydro- dynamic flow in QGP, \( {v_{2}} \) and \( {v_{3}} \) decrease as shown in the Table 1, as well as the height of the peak at \( ∆ϕ=0 \) on the residual plotting, suggesting that the influence of the factor unrelated to hydrodynamic flow reduces as ex- pected.

3. Hydrodynamic flow as a function of transverse momentum

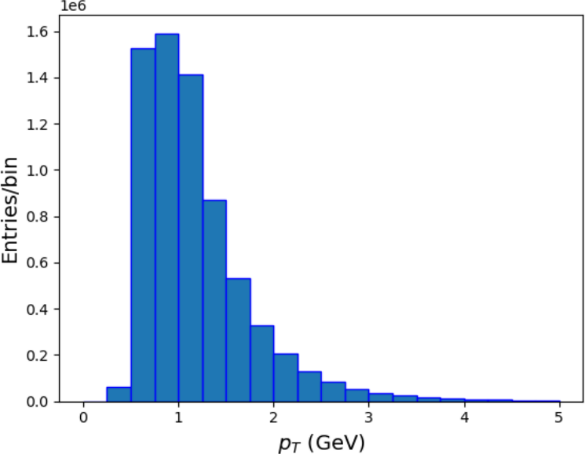
Figure 6: \( {p_{T}} \) distribution from 0 to 5 GeV

The \( {p_{T}} \) distribution from 0 to 5GeV is presented in Fig. 6. After plotting the \( {p_{T}} \) distribution of all particles from 0 to 5GeV in bins of 250MeV, we chose the \( {p_{T}} \) range from 0 to 3.2GeV to analyze the trend of \( {v_{2}} \) and \( {v_{3}} \) since insufficient events outside this range may lead to high uncertainty in data points.

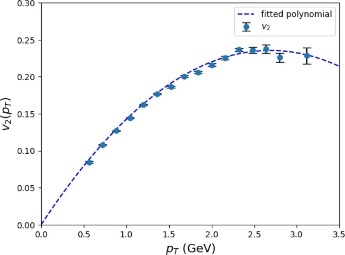
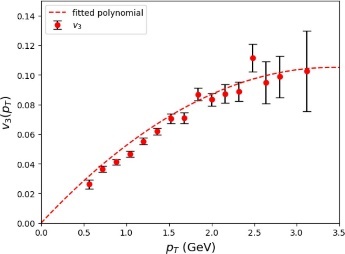
(a) \( {v_{2}} \) versus \( {p_{T}} \) (b) \( {v_{3}} \) versus \( {p_{T}} \)

Figure 7: \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \)

From the \( {v_{2}} \) versus \( {p_{T}} \) and \( {v_{3}} \) versus \( {p_{T}} \) graphs shown in Fig. 8, in general, it is evident that both the elliptic flow and triangular flow become more significant as \( {p_{T}} \) increases and level off at large \( {p_{T}} \) values. This trend agrees with past research, such as the analysis of \( {v_{2}} \) as a function of \( {p_{T}} \) of Xe \( + \) Xe and Pb \( + \) Pb collisions at the Large Hadron Collider, and Ru \( + \) Ru and Zr \( + \) Zr collisions in experiments run at \( \sqrt[]{{s_{NN}}}=200GeV \) at the RHIC by the STAR collaboration. [6, 7] In Fig. 9, the curves shown in the range of \( 0.15 GeV \lt {p_{T}} \lt 1.4 GeV \) are results predicted by the AMPT model for minimum- bias Au \( + \) Au collisions at \( \sqrt[]{{s_{NN}}}=200GeV \) and \( |Δη| \lt 1 \) with string melting and using 6 mb for the parton scattering cross section.[3] It can be observed from the graph that the trends of \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) in Pb \( + \) Pb collisions at lower transverse momentum values are similar to the results for Au \( + \) Au collisions predicted by the AMPT model.

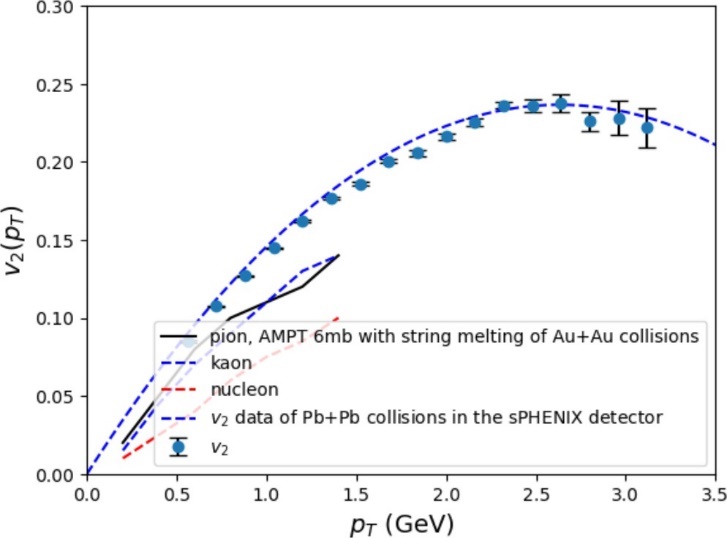
Figure 8: Comparison with the AMPT model

4. Comparison with the phobos glauber monte carlo model

Glauber model is widely used for analyzing geometric quantities in the initial state, typically represented by the impact parameter (b), number of participating nucleons ( \( {N_{part}} \) ), and number of binary nucleon-nucleon collisions ( \( {N_{coll}} \) ). [1] The Monte Carlo approach of the Glauber model is useful due to its simplicity in calculating geo- metric quantities, such as \( {N_{part}} \) and \( {N_{coll}} \) , and the pos- sibility to simulate measurable variables in experiments. [1] In this research, we applied the PHOBOS Glauber Monte Carlo code available online to generate a simu- lated dataset containing 75000 Pb \( + \) Pb collision events in order to compare the experimental results with theoreti- cal predictions.

In previous literature, it is found that \( 〈{v_{2}}〉({ϵ_{2}}) \) and \( 〈{v_{3}}〉({ϵ_{3}}) \) are linear functions in collision events generated by the Glauber Monte Carlo simulation.[2] Therefore, it is meaningful to compare \( {v_{2}} \) and \( {v_{3}} \) of the experimental data with \( {ϵ_{2}} \) and \( {ϵ_{3}} \) of the simulated data. The centrality of our set of experimental data is 40 \( - \) 50%, so only events with the same centrality in the dataset generated by the Glauber MC code were considered when making comparisons. The average value of the number of participant nucleons ( \( {N_{part}} \) ) is approximately

143. 635, and thus it would be reasonable to compare with results where 160 \( \lt {N_{part}} \lt \) 200 in previous literature. [2]

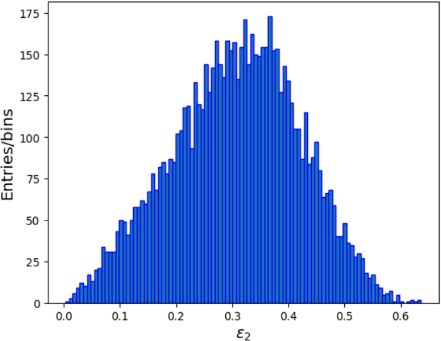
(a) Distribution of \( {ϵ_{2}} \) with centrality 40 \( - \) 50 %

(b) Distribution of \( {ϵ_{3}} \) with centrality 40 \( - \) 50 %

Figure 9: Distribution of \( {ϵ_{2}} \) and \( {ϵ_{3}} \) with centrality 40 \( - \) 50 percent

From the calculation of the weighted average of \( {v_{2}} \) and \( {v_{3}} \) , one point on each of the average \( {v_{2}} \) versus average \( {ϵ_{2}} \) and average \( {v_{3}} \) versus average \( {ϵ_{3}} \) graph can be ob- tained, which are \( (〈{ϵ_{2}}〉, 〈{v_{2}}〉)=(0.306824,0.147719) \) and \( (〈{ϵ_{3}}〉,〈{v_{3}}〉)=(0.216565,0.051076) \) . Our results provide more data to support the scaling law between the elliptic flow normalized by the inverse of the Knudsen number and eccentricity. [6]

5. Uncertainty analysis

Even though the sPHENIX detector of the RHIC has a nearly 4 \( π \) solid-angle acceptance, the pair acceptance effects have to be taken into account when analyzing the correlation function of \( ∆ϕ \) , which is observed from Fig. 1 (c). [4] In this research, the correlation function is calculated by dividing the distribution of \( ∆ϕ \) of particles in the same event by the mixed-event background distribution to reduce the influence of pair acceptance effects and random background. The \( {v_{2}} \) and \( {v_{3}} \) values of the \( ∆ϕ \) correlation function with \( |Δη| \gt \) 1, which are 0.147003 \( ± \) 0.000518 and 0.051683 \( ± \) 0.005142, have 0.352374% and 9.94911% percentage uncertainties respectively.

In addition, collision pairs with \( |Δη| \lt \) 1 were excluded from our analysis of \( {v_{2}} \) and \( {v_{3}} \) to reduce impacts of factors unrelated to hydrodynamic expansion. Besides, when analyzing \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) , only particles with 0GeV < \( {p_{T}} \lt \) 3.2GeV were considered to reduce uncer- tainties caused by the insufficient number of particles at high transverse momentum.

6. Summary

In this study, the \( ∆ϕ \) correlation function of Pb \( + \) Pb collision pairs was analyzed to investigate the elliptic flow and triangular flow in the QGP. In particular, we focused on the trend of \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) and compared our results with that predicted by the AMPT model. Our findings support the previous evidence that \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) show increasing trends at low transverse momentum values and eventually level off as \( {p_{T}} \) increases. [3] In addition, previous research mostly focused on \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) at \( |Δη| \lt \) 1. Therefore, our analysis of \( {v_{2}}({p_{T}}) \) and \( {v_{3}}({p_{T}}) \) at \( |Δη| \gt \) 1 could provide a more comprehensive understanding of the hydrodynamic properties of QGP. Finally, we also compared the weighted average of \( {v_{2}} \) and \( {v_{3}} \) with the average value of \( {ϵ_{2}} \) and \( {ϵ_{3}} \) of the data generated by the PHOBOS Glauber Monte Carlo code.

Acknowledgement

Ziru Chen and Ye Liu contributed equally to this work and should be considered as co-first authors.