1. Introduction

Vibrato on the violin is periodic changes in the pitch of the tone [1], achieved through the violinist's finger rocking back and forth on the string. It serves as a key expressive technique across music genres, contributing to classical and contemporary music's emotional depth and tonal color. Typically, discussions of vibrato involve two distinct frequencies: the frequency of the width of pitch variation \( \frac{Δf}{f} \) of around 3% and the frequency of vibrato rate of around 5 Hz [2]. An effective vibrato features a periodic pulsation of both pitch and amplitude, which are determining factors that dictate the ultimate timbre, with an ideal extent and rate to give a pleasing sense of flexibility, tenderness, and richness to the tone.

Understanding the characteristics of vibrato can help refine realistic synthesized vibrato synthesis in music production, improve educational software violin practice, and optimize the room acoustics for vibrato in performance spaces. All in all, this study aims to investigate the acoustic characteristics that differentiate naturally produced violin vibrato tones from pure, sustained tones, focusing on acoustic features including vibrato rate, extent of pitch variation, volume fluctuations, timbre, and harmonic changes through comparison with tones played without vibrato. Unlike previous research that prioritizes synthesized vibrato produced through electronic music production, this study highlights the distinct traits of natural vibrato, addressing the special effect of vibrato that uniquely shapes the violin’s timbre and distinguishes it from that of other instruments.

2. Production of vibrato tones

The instrument used for recording is a 4/4 full-size violin with nylon strings and played with a synthetic bow (Figure 1). The recordings took place in a drywall room without carpet to minimize sound absorption and reflections. The microphone was positioned approximately 20 cm away from the violin, and the recorded data was analyzed using software including Audacity, Fizziq, and Voice Memo.

Figure 1: 4/4 full-size violin with nylon strings and a synthetic bow

3. Data analysis

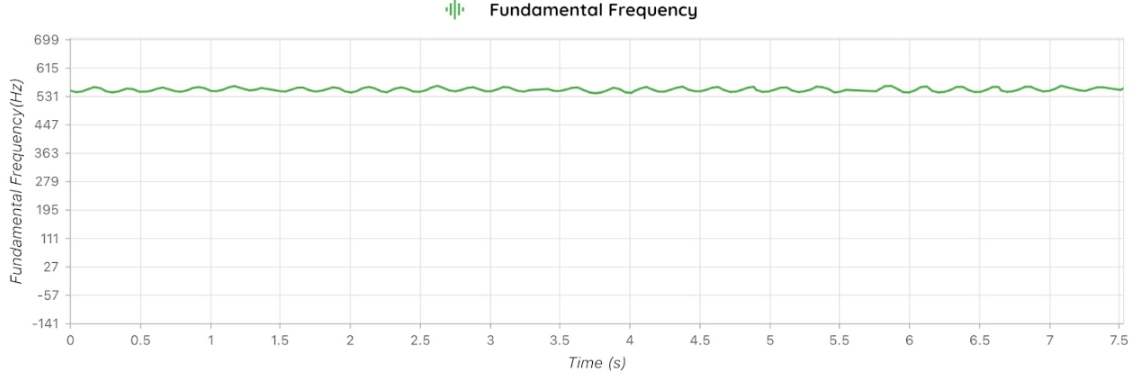
Figure 2: Frequency vs. Time graph

Figure 2 illustrates the fundamental frequency modulation by graphing the pitch oscillation against time. The relationship between the vibrato parameters and the resulting frequency modulation can be described using the mathematical equation \( f(t)={f_{0}}+A sin(2πrt), \) where \( f(t) \) is the instantaneous frequency at time \( t \) , \( {f_{0}} \) the nominal frequency without vibrato, A the amplitude of pitch variation, and \( r \) the rate of vibrato.

In Figure 2, a relatively stable oscillation is indicated by the sinusoidal waveform with an almost consistent period of 0.27 seconds which corresponds to 3.7 Hz. The overall pitch remains centered around a steady \( {f_{0}} \) , which in this case would be 554Hz C#. This shows that changes in amplitude or vibrato rate do not affect the base frequency. Altering \( {f_{0}} \) would simply shift the entire waveform up or down in a vertical translation without modifying the oscillation pattern or vibrato characteristics. These observations closely match with the intended recording of a C# (554Hz) played on the violin’s A string with added vibration. Overall, the diagram aligns with the designed feature of the recording, demonstrating a stable vibrato pattern with consistent pitch oscillations.

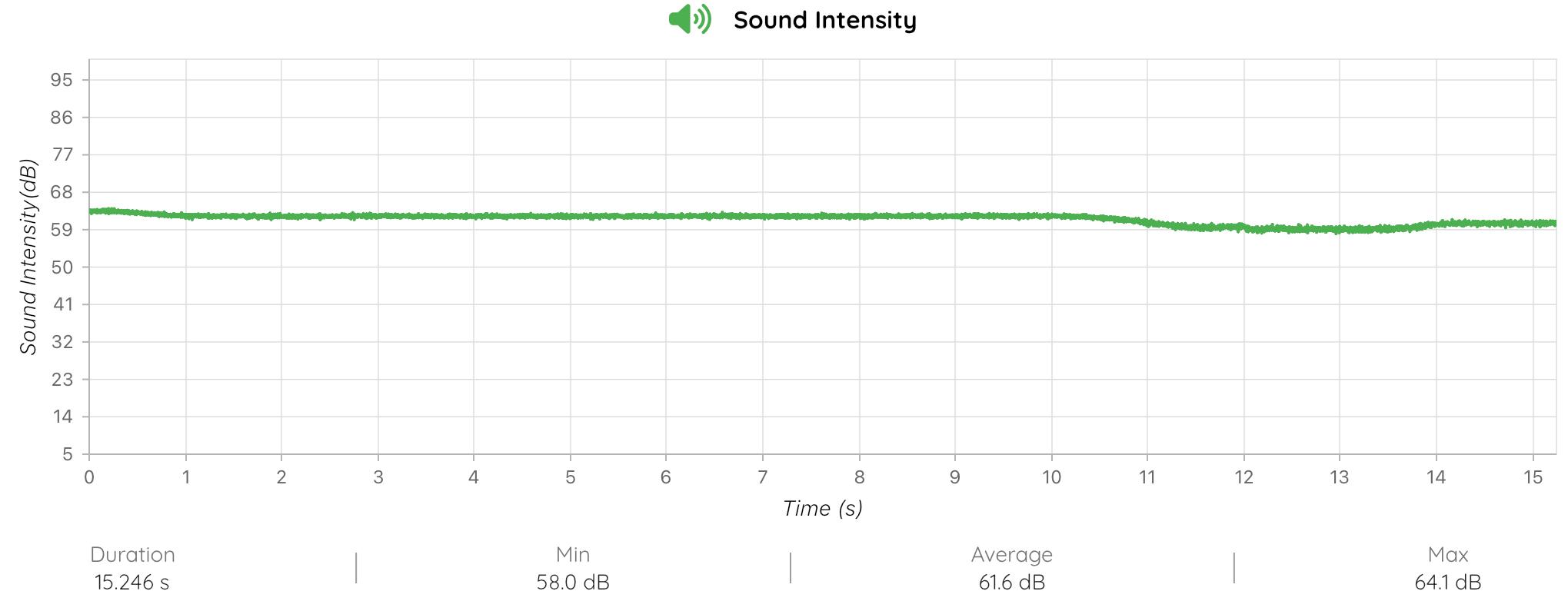
Figure 3: Amplitude vs. Time graph of a pure, sustained tone

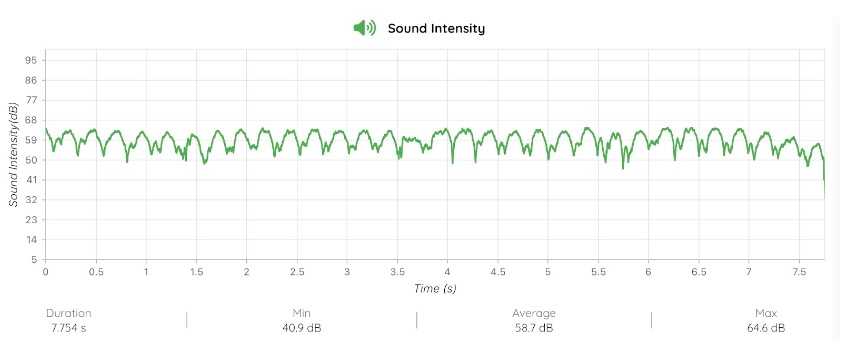
Figure 4: Amplitude vs. Time graph of a vibrato tone

The provided diagrams illustrate the amplitude modulation of both a pure sustained tone (Figure 3) and a vibrato tone (Figure 4). In both cases, the resultant amplitude can be described using the equation \( A(t)={A_{0}} [1+m sin(2πrt)] \) , where \( A(t) \) the instantaneous amplitude at time t, \( {A_{0}} \) represents the base amplitude without vibrato, m represents the modulation range, and r represents the vibrato rate.

Figure 3 shows the sustained tone in which the amplitude remains relatively stable around \( {A_{0}} \) , with minimal fluctuation, reflecting the theoretical model where \( A(t) \) would simply equal \( {A_{0}} \) due to the absence of modulation. This stability is indicated by the narrow range between the maximum (64.1 dB) and minimum (58.0 dB) sound intensity values, with an average amplitude of 61.6 dB. The minimal deviation \( {A_{0}} \) demonstrates that the term \( m sin(2πrt) \) is minimal, as expected for a pure tone without vibrato.

In contrast, Figure 4 represents the vibrato tone with a clear periodic fluctuation in amplitude, where the modulation function \( m sin(2πrt) \) becomes rather significant. The amplitude oscillates between a considerable range of highs and lows, creating an exemplary vibrato effect. The modulation range is more pronounced here, as indicated by a wider range between the maximum (64.4 dB) and minimum (49.0 dB) sound intensity levels, with an average amplitude of 58.1 dB. The regular peaks and troughs demonstrate that the amplitude varies sinusoidally between \( {A_{0}}+m sin(2πrt) \) and \( {A_{0}}-m sin(2πrt) \) .

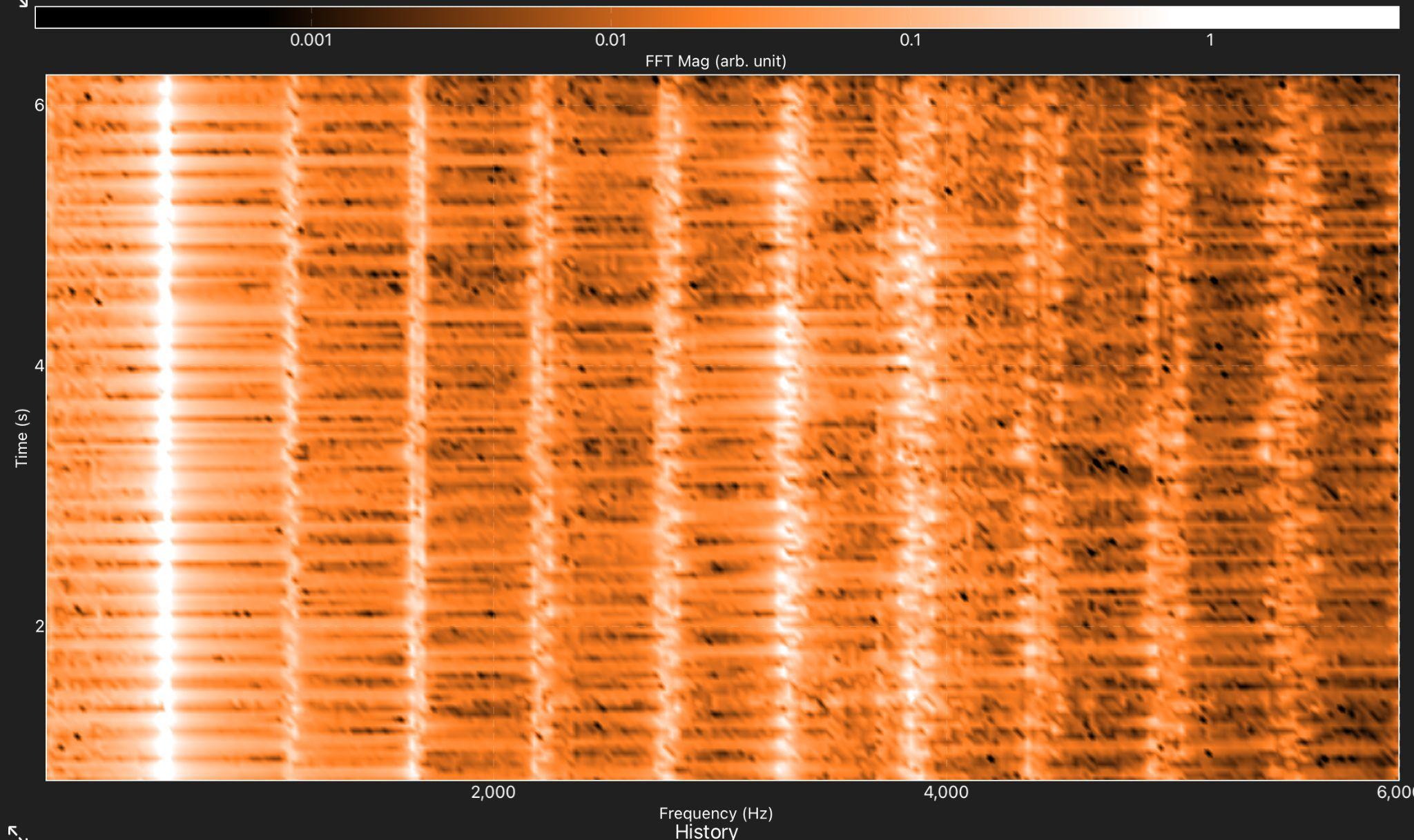
Figure 5: Spectrogram of time vs. Frequency, showing fast fourier transform

The spectrogram as shown in Fig. 5 illustrates the frequency components of a vibrato tone over time, showing multiple horizontal bands that represent both the fundamental frequency and its harmonic overtones. The equation \( y(t)=\sum _{n=1}^{N}{A_{n }}cos(2π{f_{n}}t+{ϕ_{n}}) \) models a complex waveform as a summation of n harmonic components, where each component corresponds to a specific harmonic. Here, \( {A_{n }} \) represents the amplitude of each harmonic, \( {f_{n}} \) is the frequency, and \( {ϕ_{n}} \) is the phase offset.

In the spectrogram, the parallel horizontal bands to the right of the fundamental frequency indicate harmonic overtones. Each band occurs at integer multiples of the fundamental frequency and the brightness of each of them reflects the relative intensity of each harmonic.

Furthermore, a critical factor influencing the harmonic content is the interaction between vibrato and the Helmholtz resonance. In fact, the Helmholtz resonance can vibrate a little like the air in a bottle when one blows across the top. In the case of the violin, if one sings a note near 300Hz close to the violin, one may hear the air in the body resonating around the f-hole as a result of amplified frequencies [3]. In this spectrogram, we can see the effects of this resonance near that frequency range, which contributes to the harmonics.

4. Discussion & limitation

The findings of this study are primarily applicable to violins and similar string instruments, which may limit their relevance to woodwind, brass instruments, or vocalist, due to their fundamentally different sound propagating mechanisms [4]. The controlled acoustic used in this research, while beneficial for inspecting changes in dependent variables, may not fully reflect real-world conditions where differences in room acoustics, player techniques, and instrument setups can impact vibrato characteristics. Additionally, random variations in bowing technique, including speed, pressure, and angle, have the possibility of leading to random fluctuations in the resultant tone, causing slight but noticeable inconsistent vibrato patterns that are difficult to fully account for in the analysis [5].

5. Conclusion

This study demonstrates that naturally produced violin vibrato tones exhibit periodic frequency modulation and distinct harmonic overtones that are absent in pure, sustained tones. Vibrato tones are characterized by a consistent oscillation in frequency and amplitude, creating a richer harmonic spectrum compared to the stable, unmodulated frequency and amplitude of sustained tones. These acoustic differences demonstrate the complexity of vibrato, suggesting the potential for future analysis to explore applications in music education, performance room acoustics, and instrument design that utilize results from this research.

Acknowledgment

I would like to express my sincerest gratitude towards Professor Thomas Sullivan and TA Ruoyan Zhang for their invaluable mentorship, which improved the paper immensely. The experience gained through this study has been both challenging and rewarding, and for this, I am truly thankful for their unwavering support throughout the research.