1. Introduction

Almost 30 years ago, the first hot Jupiter was discovered. A hot Jupiter is a kind of planet with Jupiter-like size and an unusually short orbit radius[1] Different from the normal gas giant planet whose orbit is far from its host star since more solid material is available for the planet to form a huge core and accrete much gas as the temperature decrease, a hot Jupiter occurs closely to the host star, sometimes less than 0.1 AU. One theory explaining why the orbits of hot Jupiters are located so close to the host star is that the giant planet initially forms in the protoplanetary disk, migrates slowly through the spinning disk [2,3]. the center, and finally reaches close to the host star. When the disk disappears, a hot Jupiter eventually occurs. Another theory suggests that a giant planet, located far from the central star after the disk disappears and following a nearly circular orbit like Jupiter, is excited by other planets. As a result, the primitive circular orbit turns into an elliptical orbit and finally forms a circular orbit much closer to its host star due to tidal effects. In this process, the orbital energy is converted by friction into heat within the planet[4].

WASP-12b is a planet reported with decaying orbit [5, p. 20], [6, p. 201]. This hot Jupiter follows an almost circular orbit [7,8] with a 1.09-day orbital period [9] a huge size of 1.90 R_Jup, and a mass of \( 1.47{M_{Jup}} \) [9]. Recent research shows that this hot Jupiter is still undergoing orbit decay with a decay rate of \( -29±3{msyr^{-1}} \) [6]. The decrease speed is so fast that the equilibrium tidal model which shows orbital decay rate as \( \frac{P}{\dot{P}}=\frac{(m_{ba}^{2})}{(2{I_{star}})}{t_{sync}}≈1.2Gyr \) is too long comparing with the rate calculated before [10, p. 201], [11] Several assumptions occurred to explain this phenomenon.

One theory maintains that as WASP-12b gets closer to WASP-12, the host star will interact with its hot Jupiter by the increased tidal dissipation due to nonlinear wave-breaking of dynamical tide. During this process, the friction turns the orbital energy into heat and shrink the orbit. However, this theory requires the main star to be a sub-giant rather than a main-sequence star and Bailey and Goodman [10] suggests that WASP-12 is more likely to be a main-sequence star rather than a sub-giant.

Meanwhile, Millholland and Laughlin [12] claims that WASP-12b’s orbital period’s rapid decrease is the result of the planetary obliquity tides. Influenced by an unseen, small-mass planet whose orbit is outside that of the hot Jupiter’s, WASP-12b maintains a large obliquity due to the spin-orbit resonance with the smaller planet. As a result, the energy of resonance is converted into heat and stored in WASP-12b due to the effect of friction.

One of the interesting possibilities is the tidal orbital decay, where the angular momentum of the hot Jupiter is directly transferred to its host star due to the gravitational interaction between the planet and the star’s tidal bulge (equilibrium tide). The mechanisms that convert stellar tidal oscillations into heat within the star are unclear [13].

In this paper, we present new transits and occultations data of WASP-12b, as well as previous data (Section 2). Based on the data, we compare the orbital decay model and the apsidal precession model for the better fitted one (Section 3). Finally we discuss the possible tidal orbital decay and prospects for further observations (Section 4).

2. Data collection

2.1. Transit observation

We used light curve data of WASP-12b from the Transiting Exoplanet Survey Satellite (TESS). TESS has four identical 10-cm-diameter cameras. Each has a field of view of \( 24×24 {deg^{2}} \) , combining in a line to \( 2304 de{g^{2}} \) field of view, corresponding to a sector on celestial sphere. The cameras detect the flux of light on their CCDs, which form images covering \( 4096×16384 \) pixels. The CCDs produce continuous stream of images with an exposure time of 2 s, and the images will be binned into a cadence for several optional periods. TESS faces a sector for two spacecraft orbits, each lasting for 13.7 days. During every orbit, it spends about 2.2 days sending its data back to the earth, when observation is interrupted [14]

We firstly chose the data sets with 120s cadence between 2019 December and 2023 December, which includes 6 sectors. To fit the data point, we used a standard model [15] to the data from each transit.

Then, we linked all of the latest 132 transit data sets, used a single eclipse model with WASP-12 and ruled out the time scope where no light curve was collected. Meanwhile, we dismissed 14 sets of data not including enough data points(less than 80% of the data median number of all data), leaving 118 sets of valid transit data.

We fixed the orbital period on 1.091420078 days and let other system parameters vary freely to get the best fit. Finally, we got all the fitting curves of valid data sets, as well as their mid-transit time and uncertainty. We chose the mid-transit time T₀ = 2456305.455609 as a reference [6], so that we calculated the epoch, namely the orbit number of all transit data. Table 1 consists of the fitted parameters for each sector, along with the combined parameters.

Table 1: The fitted parameters for lightcurve data in each sector and combined parameters

We combined the transit timings we obtained from TESS data and previous transit-timing data from Ivshina and Winn [16] to study the trend of mid-transit time along with the orbit number. A portion of both data are provided in Table 2.

Table 2: A portion of transit data

NOTE: The entire data of transit and occultation midtimes are available from the authors in a machine readable format.

2.2. Occultation observation

In comparison to the transits (primary eclipses), the individual secondary eclipse events are not detectable by TESS with a sufficiently high signal-to-noise ratio for reliable timing measurements. Therefore, instead of fitting the data for each individual occultation within each sector, we combined all full and interrupted occultation events within a TESS sector to calculate a single effective mid-occultation time.

We selected all valid data within one referenced transit duration from the predicted mid-occultation time, and retained only those data ranges that contain enough data points (more than 80% of the median number across all such data ranges). We median-normalized each of the secondary eclipse events and phase-folded them by centering them at half a phase later than our reference transit time. To further reduce noise, we binned the time with a bin size of 10, indicating a 10-minute cadence.

For each sector, we fitted a trapezoid dip with fixed ingress and egress time and full transit duration, as best fitted and derived by Wong et al [17]. We derived the out-of-transit base level by taking the median of the data outside the duration time of the occultation and within the selected folded time.

We fitted for the mid-occultation time, \( {T_{occ}} \) . The orbit number of \( {T_{occ}} \) for each sector was set to the secondary events closest to the mid-time of the time series. The best-fit timings for the six TESS sectors were presented in section 3.

3. Data analysis

We have gathered all the transit and occultation data, with the addition of the new data from section 2. For the sectors that are previously mentioned in other literature, we have decided to use our derived mid-time for methodological consistency. Most of this data was compiled by Yee et al [18] with the addition of occultations from CHEOPS from Wong et al [19]. We have added 118 new transits and 6 new occultations into the catalog from sectors 20, 43, 44, 45, 71, and 72. We want to emphasize that the data in the table is based on the BJD_TDB system, calibrated to the same reference mid-time.

We applied three models to fit the transit and occultation data mentioned in Patra et al[6]. The first is linear model, assuming a circular orbit and constant orbital period:

\( {t_{tran}}(E)={t_{0}}+EP \)

\( {t_{occ}}(E)={t_{0}}+\frac{P}{2}+EP \)

Table 3: Occultation events for WASP-12b from this work

where E is the epoch from a selected reference orbit, and t0 is the mid-transit time of this reference orbit [6]

The second is quadratic model, also assuming a circular orbit, yet the orbital period to be decaying constantly with time:

\( {t_{tran}}(N)={t_{0}}+{NP_{s}}-\frac{{eP_{a}}}{π}cosω \)

\( {t_{occ}}(N)={t_{0}}+\frac{{P_{a}}}{2}+{NP_{s}}+\frac{{eP_{a}}}{π}cosω \)

\( ω(N)={ω_{0}}+\frac{dω}{dN}N \)

\( {P_{s}}={P_{a}}(1-\frac{1}{(2π)}\frac{dω}{dN}) \)

where P_s is the sidereal period, P_a is the anomalistic period, and ω is the argument of pericenter.

We used the emcee code to conduct MCMC sampling of the posterior distribution in parameter space to stabilize the fitting result, following the approach outlined in Yee et al [20]. We employed broad uniform priors on all parameters and ran the MCMC with 100 walkers. The initial 40% of steps were discarded as burn-in. This process was run for over 10 autocorrelation times. We also examined the posteriors and calculating Geweke scores for each chain [21] to ensured convergence. The fit results are presented in Table 4, where we minimized χ² to fit the model in all three cases.

As expected from previous literature [6,19,20], a linear model does not fit the data well; here, the linear model has a minimum χ² of 1348.2, with 251 degree of freedom. Compared to the linear model, the χ² in quadratic model and sinusoidal model has much smaller discrepancy, each with a χ² of 330.27 and 423.499. While ∆χ² = 93.23 itself is expected, it’s significantly larger than previous literature[6, p. 20] (∆χ² = 5.5[6], ∆χ² = 12.1[20]). This can be contributed to the longer observation period and further boost our confidence of the potential orbital decay of WASP-12b.

To show the superiority of the quadratic model which includes less parameters than sinusoidal model, we use Bayesian Information Criterion (BIC), defined as followed:

\( BIC≡{χ^{2}}+klogn \)

where k is the quantity of free parameters and n is the quantity of data points. We can see a ∆BIC in this case is 104.10. In order to better illustrate where the distinction comes from, we plotted out the residual plot for transits and occultations separately (see Figure 1 , using the linear model as baseline. It can be difficult to determine whether the decaying trend is solely part of the long-term precession when only examining transits. However, upon analyzing the occlusions, we observe a clear deviation from the predicted model. This strengthens our confidence in the quadratic model.

4. Discussion about tidal orbital decay

Regarding the tidal orbital decay we mentioned earlier, we used the simplified “constant phase lag” model [2] that considers the equilibrium tide. Under the assumptions that the orbit is circular (eccentricity = 0), the planet’s mass is constant, and the orbital angular momentum is significantly greater than stellar angular momentum, we applied equation (20) from Goldreich & Soter :

\( \frac{da}{dt}=-\frac{9}{2}{(\frac{G}{{M_{⋆}}})^{(\frac{1}{2})}}\frac{R_{⋆}^{5}}{{Q_{⋆}} \prime }\frac{{M_{p}}}{{a^{(\frac{11}{2})}}} \)

where a is the orbital semi-major axis, and Q^′⋆ is the “reduced” tidal quality factor described as \( Q_{⋆}^{ \prime }=\frac{3}{2}\frac{{M_{p}}}{{M_{⋆}}}{(\frac{a}{{R_{⋆}}})^{5}}\frac{n}{|\dot{n}|} \)

where Q_⋆ is the tidal quality factor and k₂ is the Love number. Applying Kepler’s third law, we could get the decay rate of period:

\( {t_{tran}}(E)={t_{0}}+{EP_{s}}-{eP_{a}}πcosω \)

\( {t_{occ}}(E)={t_{0}}+\frac{{P_{a}}}{2}+{EP_{s}}+\frac{{eP_{a}}}{π}cosω \)

\( ω(E)={ω_{0}}+\frac{dω}{dE}E \)

\( {P_{s}}={P_{a}}1-\frac{1}{2π}\frac{dω}{dE} \)

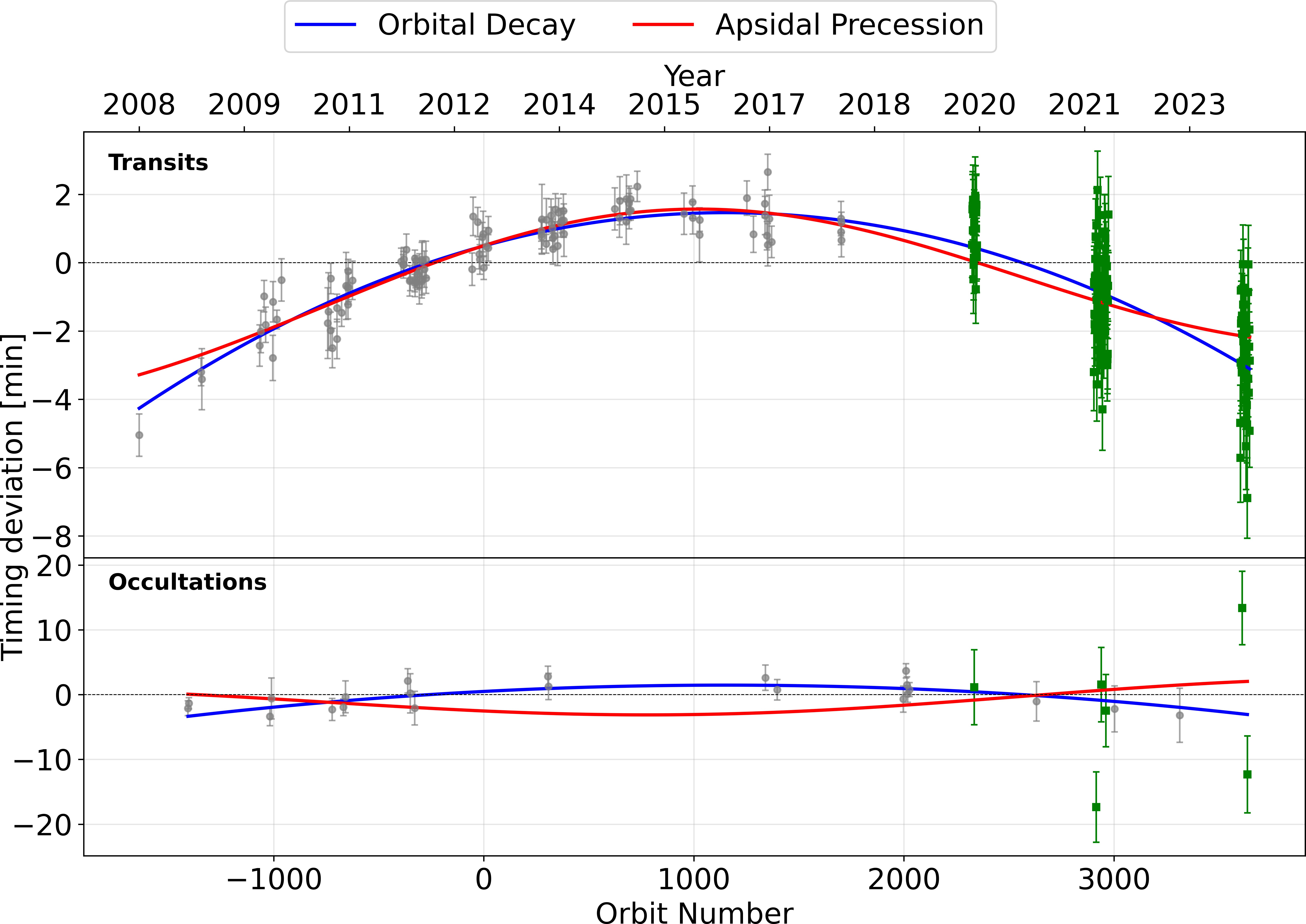
Figure 1: Combined O-C (Observed minus Calculated) diagram for transit and occultation timing deviations of WASP-12b. The top panel shows transit timing deviations, while the bottom panel displays occultation timing deviations. Gray circles represent previous observations, and green squares indicate new observations from this work. The blue line represents the best-fit quadratic model, and the red line represents the best-fit sinusoidal model. The dashed black line at y=0 represents the linear ephemeris. Error bars represent 1σ uncertainties

Using the measured decay rate of period of 29.5ms/yr, we obtain the reduced tidal quality factor Q^′⋆ of WASP-12 to be:

\( {Q_{star}}≈1.66±0.06×{10^{5}} \) (7)

We could then calculate the decay rate of orbital energy and the decay rate of angular momentum

\( \frac{dE}{dt}=\frac{{(2π)^{(\frac{2}{3})}}{M_{p}}}{3}{(\frac{{GM_{⋆}}}{P})^{(\frac{2}{3})}}\frac{1}{P}\frac{dP}{dt}=-5.0×{10^{23}}W \)

\( \frac{dL}{dt}=\frac{{M_{p}}}{3{(2π)^{\frac{1}{3}}}}{(\frac{{GM_{⋆}}}{P})^{\frac{2}{3}}}\frac{dP}{dt}=-7.5×{10^{27}}kg{m^{2}}{s^{-2}} \)

where \( {M_{star}}=1.434×0.110{M_{sun}} \) , and \( {M_{planet}}=1.434×0.110{M_{sun}} \) [22]. These results are similar to Yee et al[13] , and are obvious while a planet’s orbit is decaying for tidal interation.

However, the magnitude of Q^′⋆ is smaller than expected one in earlier studies[23]. Millholland & Laughlin[12] indicates this might result from a likely-existing planet orbiting the same host star and perturbing the orbit of WASP-12b. Future observations on WASP-12 are necessary to verify this hypothesis.

5. Summary

Our analysis of WASP-12b’s orbit, incorporating the latest TESS data from Sectors 20, 43, 44, 45, 71, and 72, along with previously published observations, strongly supports the quadratic model. The key findings of our study are:

We analyzed 118 new transit observations and 6 new occultations, significantly expanding the available dataset for WASP-12b. The quadratic model provided the best fit to the data, with a ∆BIC of 104.09 compared to the linear model, strongly favoring orbital decay over apsidal precession. We calculated an orbital period decay rate of \( \dot{P}=-29.5\frac{ms}{yr} \) , consistent with previous studies and indicating a uniform decay of WASP-12b’s orbit. The reduced tidal quality factor for the host star was determined to be \( {Q^{ \prime }_{⋆}}=1.66±0.06×{10^{5}} \) aligning with earlier research and supporting the orbital decay hypothesis. These results reinforce the uniqueness of the WASP-12 system, as it remains one of the clearest examples of rapid orbital decay among hot Jupiters. The consistency of our findings with previous work strengthens the case for ongoing tidal interactions between WASP-12b and its host star.

Table 4: Timing model fit parameters

NOTE—Uncertainties in parentheses are the 1-σ confidence intervals in the last two digits.

The rapid orbital decay of WASP-12b continues to challenge our understanding of star-planet interactions and tidal dissipation mechanisms. Future observations and theoretical work will be crucial to fully explain the physical processes driving this decay and to predict the ultimate fate of the WASP-12 system. This research not only advances our knowledge of WASP-12b but also contributes to our broader understanding of hot Jupiter evolution and the dynamics of close-in exoplanetary systems.

6. Statement of work

This research was a collaborative effort among multiple contributors. Zoutong Shen was the primary developer, responsible for all coding, data cleaning, analysis, and modeling, as well as partial data collection. Shen also drafted sections on data analysis and collection and created most of the figures and tables in the main text. Hao Meng outlined the paper structure, authored the Abstract, parts of the Data Collection and Analysis sections, equations, Discussion, and Acknowledgement, and organized all data collection materials. Yishan Wu contributed to the literature review and wrote portions of the Abstract, Introduction, Discussion, and equations. Mei Zhang assisted with the literature review and composed part of the Introduction. Yunhe Fei contributed to writing the data analysis and data collection sections. All authors reviewed and approved the final manuscript.

Acknowledgments

We appreciate Professor Joshua N. Winn, who provided necessary instruction about the theory on the transit and occultation of WASP-12b, and python codes to deal with the data. The authors are very grateful to teaching assistant Xinyue Huang, who provided inspiring guidance and discussion about the technical skills of the codes and paper. We also gratefully acknowledge all the anonymous researchers in the Science Processing Operations Center (SPOC) for providing clear and essential light curve data of WASP-12. We thank CIS, which organized and arranged the summer camp for the authors to discuss and finish this paper. The convenient place for this summer camp is supported by Shanghai Jiao Tong University.