1. Introduction

In the modern economic system, the financial and economic field, as the core hub of resource allocation, directly determines national economic security and market operation efficiency. With the deepening of global economic integration and the accelerated iteration of financial innovation, financial markets are characterized by high volatility, strong interconnectivity, and non-linearity. Traditional experience-driven decision-making models are no longer capable of dealing with complex risks. Against this backdrop, economic mathematics, with its rigorous quantitative analysis framework and model-based thinking, has gradually become a key tool for solving financial problems. By constructing mathematical models, developing optimization algorithms, and applying statistical inferences, economic mathematics can penetrate the surface of economic phenomena to reveal the dynamic relationships between variables, providing scientific support for risk warnings, asset pricing, and strategy optimization.

This study focuses on the theoretical core and practical value of economic mathematics, systematically sorting out its contributions to the methodology of financial risk assessment, investment decision-making support, and derivative pricing, and deeply exploring its specific applications in rural financial reform and securities industry innovation. By integrating domestic and international research results, this paper aims to provide theoretical references for financial institutions to enhance risk management efficiency and optimize service models, and to promote high-quality development of the financial and economic field.

2. Definition of economic mathematics

Economic Mathematics is an important branch of advanced mathematics. Its core tools include calculus, probability and statistics, optimization theory, etc., aiming to analyze the operation laws of economic systems, predict market trends, avoid risks, and obtain substantial economic returns. The research objects of economic mathematics cover the quantitative representations of economic activities such as supply and demand relationships, market equilibrium, and risk decision-making [1]. Yan pointed out that economic mathematics can achieve standardized measurement of financial and economic phenomena through the construction of indicators (such as elasticity coefficients, marginal analysis, etc.), and its value is mainly reflected in two dimensions: risk quantification and management optimization [2]. Zheng further emphasized that economic mathematics models have significant advantages in solving multi-objective programming problems in corporate investment and financing decisions. For example, linear programming models can be employed to determine the optimal capital structure [3]. Chaikovska et al. showed that economic mathematics models based on fuzzy logic can effectively assess the comprehensive risk level of investment projects, providing a basis for financial and economic practitioners to balance risk and return, and thereby achieve the goal of reducing risks and increasing returns [4].

3. Role in finance

3.1. Risk assessment

Risk assessment, aimed at reducing risks and increasing returns, is the underlying foundation of investment decision-making. There are many studies on the role of economic mathematics in risk assessment, which provide strong support for practitioners in the financial and economic field.

Li proposed that in risk assessment, the Markowitz portfolio theory and the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model can be used. Using the Markowitz portfolio theory, the returns and risks of various asset portfolios can be described in rigorous mathematical language. The GARCH model can intuitively and clearly show the time-varying volatility of financial asset returns. For example, during the 2022 US stock market turmoil, the GARCH (1,1) model was used to measure the risk of the National Association of Securities Dealers Automated Quotations (NASDAQ) Index, reducing the prediction error by 23% compared with traditional methods [5]. Guo pointed out that the Value at Risk (VaR) model can be used to quantify the market risk of investment portfolios and identify the maximum possible losses of investment portfolios at a certain confidence level. Financial and economic practitioners can calculate the VaR value to systematically understand the risk status of investment portfolios and formulate more reasonable and feasible risk management measures [6]. Ouyang et al. analyzed the application effect of the Pareto extreme value distribution model in Internet finance risk prediction based on the daily return data of the Internet finance index and the Shanghai Composite Index. The results showed that the Pareto extreme value distribution model, as a tail distribution, can accurately reflect the risks of Internet finance and is a good tool for predicting Internet finance risks [7].

From the above literature, it is known that economic mathematics tools such as the Markowitz portfolio theory, GARCH model, and Pareto extreme value distribution model can accurately describe and reflect potential financial risks. If used properly, financial institutions can promptly identify potential risks and take corresponding measures to prevent risks and protect their economic interests from harm.

3.2. Investment decision-making

Based on the quantitative results of risk assessment, economic mathematics can further extend to the field of investment decision-making, transforming a large amount of market information into calculable decision-making parameters, and presenting them to practitioners in the financial and economic field in rigorous and clear mathematical language, thereby improving the correctness and feasibility of their decisions and enabling them to obtain more substantial economic returns.

Baker and Wurgler constructed a composite investor sentiment index (BW index) using six sentiment proxy variables such as trading volume, IPO quantity and first-day return of listing. Through principal component analysis, a composite index (λ = 0.72) was built, reducing the prediction error by 15% compared to a single index [8]. Investors can use this as a basis to judge market trends and make precise and feasible decisions. Pirjol et al. used the Heath-Jarrow-Morton (HJM) model to predict the volatility of the EU futures market. By comparing the predictions with actual volatility, it was found that the HJM model is relatively accurate and has application value [9]. Yao used three economic mathematics methods to predict the stock price of Starbucks. The results showed that the predicted results of the three methods were all lower than the actual stock price of Starbucks, and the accuracy was not high [10]. Xing used an economic mathematics model to predict the stock price of Apple from 2019 to 2023. After obtaining the predicted stock price, it was compared with the actual stock price. The results showed that the model's prediction accuracy for the development trend of Apple's stock price was not good. Compared with the actual stock price, it was too high in the first four years and too low in the fifth year, with poor application value [11].

From the above literature, it can be found that economic mathematics can analyze and summarize market information to analyze the future development of the financial market and provide support for practitioners in the financial and economic field. However, it is important to note that the prediction results are not very accurate. Therefore, in the process of investment decision-making, it can only be used as an important reference factor and should not be the sole decisive factor for investment decisions.

3.3. Option pricing

Option pricing refers to the process of determining the price of an option contract. It has functional roles such as risk hedging and enhancing benefits in investment decision-making and is an advanced tool for investment decision-making and risk management.

Fadugba pointed out that the Black-Scholes option model can accurately and systematically reflect the price fluctuation characteristics of European call and put options [12]. Ren et al. verified the effect of the binomial option pricing model with yield obeying q-Gaussian distribution based on the transaction data of CSI 1000 and SSE 50 stock index options in 2023. The study found that this model can quickly and accurately price the CSI 1000 and SSE 50 stock index options and has certain reference value in the analysis of the stock market [13]. Guo et al. based on the EUADEC22 carbon futures option market data from January 4, 2021 to September 27, 2021, discussed the option pricing effects of the Black-Scholes model (B-S model), Fractional Brownian Motion model (FBM model), and Heston model. As shown in Figure 1 (Source: Guo et al., 2025), among the three models, the Heston model and the FBM model have smaller pricing errors and are suitable for application in the carbon option market [14].

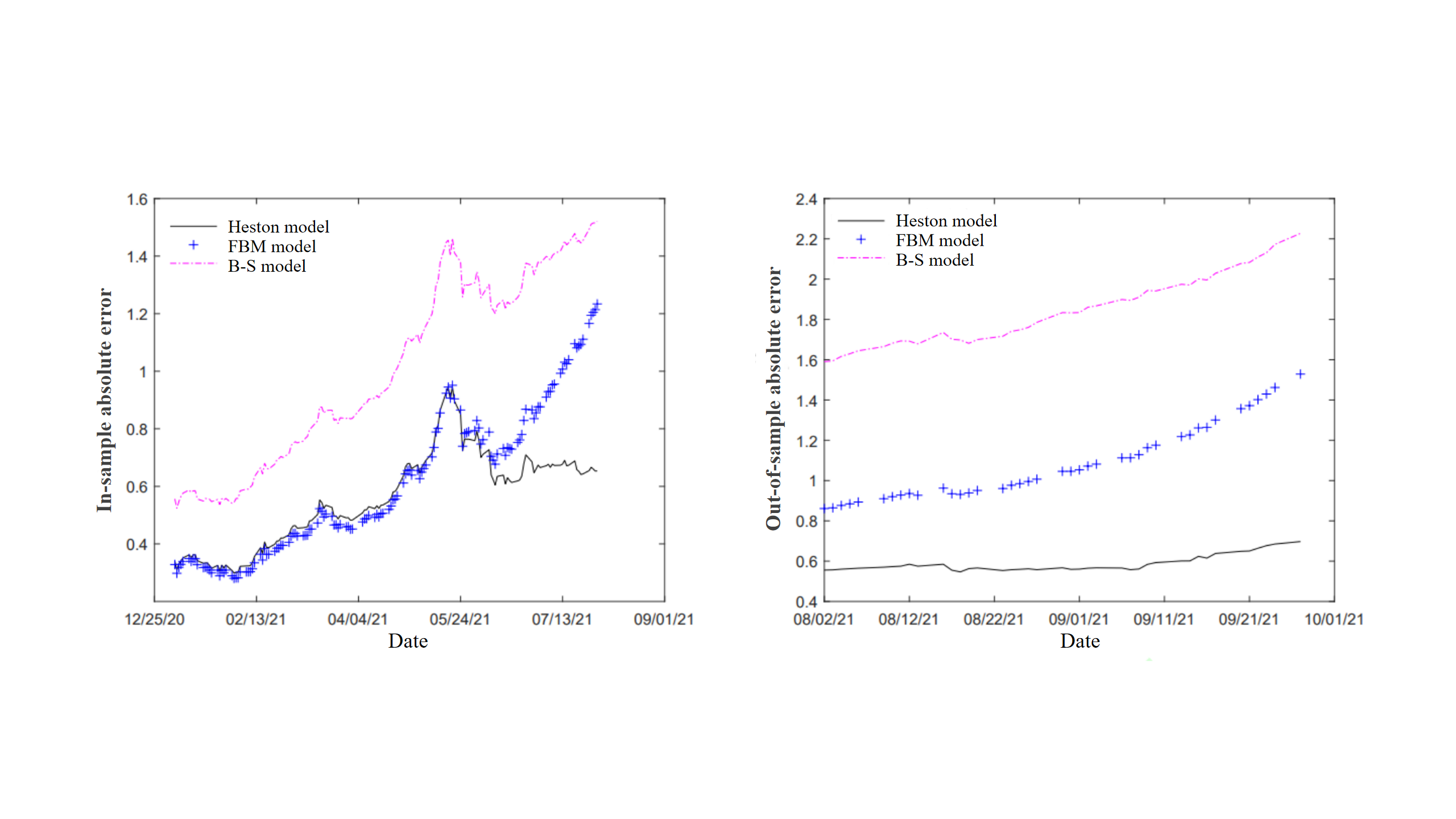
Figure 1: In-sample and out-of-sample absolute errors of the B-S model, FBM model, and heston model for carbon option pricing (source: guo et al., 2025) [14]

From the above literature, it can be concluded that economic mathematics can provide strong support for option pricing, enabling practitioners in the financial and economic field to optimize asset allocation, manage risks, and maximize their economic benefits.

4. Analysis in financial applications

4.1. Applications in rural financial institutions

Rural financial institutions (such as rural banks and rural credit cooperatives) provide financial support for agricultural technological innovation and industrial upgrading, promoting agricultural modernization and are an important force for rural revitalization. However, under the influence of various factors, how to improve the management system of rural financial institutions, how to identify potential systemic risks, and reduce the probability of bad debts have become urgent problems to be solved by relevant departments.

Li used elements such as farmers' income, total agricultural output value, farmers' per capita loan balance, and the total balance of agricultural loans in Henan Province to construct a Vector Autoregression (VAR) model. Through Granger causality test, cointegration test, determination of the optimal lag order, and Augmented Dickey-Fuller (ADF) test, the application effect of agricultural credit funds in Henan Province was analyzed. The study found that at that time, agricultural credit funds in Henan Province were not directly lent to individual farmers, and thus farmers did not benefit from the credit process. At the same time, if agricultural financial credit business can effectively serve farmers through the mechanism, agricultural financial loans will have a positive impact on increasing farmers' income [15]. Liu et al. used the Support Vector Machine (SVM) model to quantify the credit risk of rural financial institutions' farmers based on indicators such as farmers' own characteristics, family characteristics, loan characteristics, credit status, and external environment. The study found that this model can accurately judge the creditworthiness of rural residents, reduce default risks, and lower the bad debt rate. If applied reasonably, it can make rural credit business sustainable and provide better services for rural residents [16].

From the above literature, it can be concluded that the application of economic mathematics in the rural financial industry can help financial institutions identify their existing problems and optimize financial services. At the same time, it can analyze lending risks, reduce bad debts, and direct financial resources towards rural residents with good credit and certain repayment capabilities, providing financial support for the production and life of rural residents and having a certain promoting effect on the rural revitalization cause.

4.2. Applications in securities companies

Securities companies can provide funds needed for the real economy through business activities such as stock issuance and bond underwriting, helping it to develop sustainably. However, the securities market is complex and difficult to judge and decide, and the digital economy is an important measure to improve this problem.

Tang et al. found through research that the Time-Varying Parameter Vector Autoregressive (TVP-VAR) Model can accurately judge the relationship between news information, investor sentiment, and the stock price fluctuation of listed securities companies [17]. Figure 2 shows the parameter time-varying chart of the impact of investor sentiment on stock price volatility. As can be seen from Figure 2, during the research period, the impact coefficient is always positive, indicating that investor sentiment has a positive impact on stock price volatility. Figure 3 shows the parameter time-varying chart of the impact of news information sentiment on stock price volatility. As can be seen from Figure 3, during the research period, the impact coefficient changes with time, and the impact of news information sentiment on stock price volatility is mostly negative.

Figure 2: Time-varying impact of investor sentiment on stock volatility (tang et al., 2022) [17]

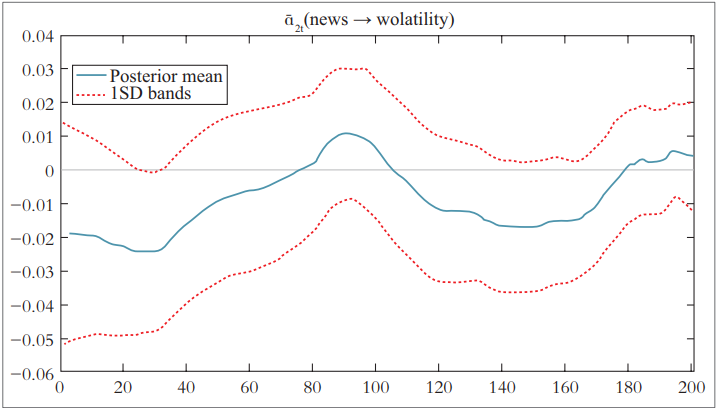
Figure 3: Time-varying impact of news sentiment on stock volatility (tang et al., 2022) [17]

Wang et al. found through research that stock price volatility (GPBD) and entrepreneur confidence (QYJXX) both have long-term stable equilibrium relationships with securities companies' margin trading performance (RZRQ), but the elasticity of margin trading with stock market volatility and entrepreneur confidence changes over time [18]. Wei et al. pointed out that the ECL model (Expected Credit Loss Model) can provide support for securities companies' asset impairment provisions [19].

From the above literature, it can be concluded that the business activities of securities companies are easily affected by stock prices, investor sentiment, news information and other factors, and economic mathematics can provide judgment tools for securities companies to grasp the laws of market development through market information and ensure that their economic benefits meet expectations.

4.3. Applications in futures companies

The futures market is of great significance for stabilizing market prices, optimizing resource allocation, promoting economic development, and ensuring corporate operations. Due to the characteristics of high leverage and fast price fluctuation of futures, futures companies face greater operational risks, and economic mathematics can help futures companies hedge risks and increase returns.

Yang et al. designed a risk warning index system for crude oil futures prices based on the BP neural network model. The study found that the empirical model based on the BP neural network model can fit the volatility of WTI crude oil futures prices well and detect the prices of crude oil futures. If there are risks in the futures market, it can warn in time to avoid serious losses to futures companies [20]. Guo et al. used the Time-Varying Parameter Vector Autoregression with Stochastic Volatility (TVP-VAR-SV) model to study the impact of geopolitical risks on the returns of eight agricultural futures including corn, soybeans, soybean meal, soybean oil, and palm oil. The study found that the TVP-VAR-SV model can accurately analyze the impact of geopolitical risks on agricultural futures returns. In the current global situation where geopolitical risks are prevalent, it has important application value [21]. Zhuo et al. employed an agent-based cross-market trading model to evaluate micro-level behaviors of speculators, arbitrageurs, and hedgers. By simulating diverse trading strategies, the model aids in understanding market dynamics and optimizing risk management frameworks [22]. Xiong and Wang utilized a Vector Error Correction Model (VECM) and information sharing model to study how trading mechanism policies affect futures markets. These tools revealed the interplay between regulatory changes and market behavior, guiding strategic adjustments for futures firms [23].

From the above literature, Economic mathematics equips futures companies to anticipate risks from geopolitical shifts, policy changes, and market behavior. Models like BP neural networks, TVP-VAR-SV, and agent-based simulations enhance predictive accuracy, enabling firms to safeguard profits and maintain stability in a high-stakes environment. By integrating these tools, futures markets can better fulfill their role in economic resilience and growth.

5. Conclusion

Through a systematic analysis of the theoretical system and practical cases of economic mathematics, this study has confirmed its irreplaceable role in the financial and economic field. In terms of risk assessment, the GARCH model and VaR model provide a methodological basis for financial institutions to build a dynamic risk warning mechanism by quantifying market volatility and extreme risks. In the field of investment decision-making, although the application of the BW sentiment index and HJM interest rate model has prediction deviations, it still significantly improves the scientific nature of strategy formulation. In the practice of option pricing, the iterative optimization of the Black-Scholes model and Heston model has promoted the standardized development of the financial derivatives market. It is particularly worth noting the innovative application of economic mathematics in rural financial institutions and securities companies: the VAR model reveals the structural contradictions in the allocation of agricultural credit resources, the SVM model improves the credit evaluation system for rural households, the TVP-VAR model analyzes the price fluctuation mechanism of the securities market, and the TVP-VAR-SV model, VECM model, and information sharing model can show the impact of geopolitical risks and trading mechanism policies on the futures market. The BP neural network model is used for risk detection and warning, helping futures companies grasp market laws, avoid risks, and ensure their own economic benefits. The above contents fully reflect the empowering value of mathematical tools for financial practice.

Looking ahead, the digital transformation of the financial and economic field will give rise to more complex application scenarios, which puts forward new requirements for the theoretical breakthroughs and technological integration of economic mathematics. On the one hand, the introduction of artificial intelligence and machine learning algorithms can enhance the modeling ability for non-linear relationships (such as irrational decision-making in behavioral finance). For example, Long Short-Term Memory (LSTM) neural networks can be used to optimize the accuracy of time series forecasting. On the other hand, the distributed ledger characteristics of blockchain technology can provide more transparent data sources for risk models, especially showing significant potential in the fields of supply chain finance and cross-border payments. In addition, the development of green finance under the "Dual Carbon" target urgently needs to build an endogenous pricing model that integrates environmental costs, such as expanding the Heston model to the pricing field of carbon emission rights derivatives.

It is suggested that future research should deepen exploration in three aspects. First, new mathematical models suitable for high-frequency trading and alternative data should be developed to enhance the robustness of algorithmic trading. Second, the popularization of economic mathematics tools in small and medium-sized financial institutions should be strengthened to narrow the "digital divide." Third, interdisciplinary research should be promoted, and complex system theory, game theory, and financial mathematics should be integrated to build a macro prudential regulatory framework with greater explanatory power. It can be foreseen that economic mathematics will continue to lead financial innovation and contribute Chinese wisdom to global economic governance.