1. Introduction

In the research on coal multimodal transportation, scholars typically focus on two aspects: model construction and algorithm optimization [1]. In terms of model development, researchers generally establish multi-objective decision-making models aimed at minimizing total transportation costs and reducing carbon emissions. For algorithm optimization, efforts are primarily dedicated to improving methodologies such as genetic algorithms to enhance the accuracy and reliability of solutions. Regarding model construction, Li Na proposed a coal multimodal transportation optimization model incorporating external costs, solved using the NSGA-II algorithm, and further analyzed the impact of external costs on optimal transportation routes [2]. Yang Yang developed a multimodal transportation path optimization model for coal logistics based on the objective of minimizing economic costs and solved case studies using genetic algorithms [3]. Zhang M constructed a multi-objective fuzzy chance-constrained model under conditions of time uncertainty [4]. In the realm of algorithm optimization, Zhou Jiajie introduced an improved K-shortest path algorithm based on arc-path modeling and validated it through case studies on coal transportation in Shanxi Province [5]. Zhang H proposed a novel solution strategy utilizing the sparrow search algorithm. Zheng C enhanced the particle swarm optimization algorithm [6], while Huang Qin optimized the Harris hawk algorithm [7]. Additionally, Wan Jie designed an improved fireworks algorithm and developed a multi-objective optimization method based on the DE-NSGA-I algorithm [8].

Against this backdrop, this paper constructs a multi-objective optimization model considering transportation costs, carbon emissions, and transit time under the context of Jining Port's operational launch, aiming to provide a more scientific planning framework for coal transportation networks.

2. Model construction

Based on the aforementioned assumptions and aligned with relevant literature and practical scenarios, the parameters and variables of the proposed model are defined as follows:N: Set of all nodes in the transportation network;M: Set of transportation modes, M={1,2,3}, where 1: road transport, 2: rail transport, 3: waterway transport;i: Origin node of goods, i∈N;j: Destination node of goods, j∈N;k: Transportation mode,k∈M;Q: Total coal transportation volume;T_ij: Total permissible transportation time;C_ijk: Transportation cost from origin ii to destination j using mode k;E_ijk: Carbon emissions from origin i to destination j using mode k;T_ijk: Transportation time from origin i to destination j using mode k;L_ijk: Transportation distance from origin ii to destination jj using mode k;V_k: Average speed of transportation mode k;W_j: Unit inventory cost at destination j;e_k: Unit carbon emissions of transportation mode k;e_k1k2: Unit carbon emissions during mode transfer from k₁ to k₂;s_k1k2: Unit transfer cost for shifting goods from mode k₁ to k₂;c_k: Unit freight rate of transportation mode k;e: Unit carbon tax value (tax per unit of carbon emissions);p: Unit penalty cost for delivery delays (cost per unit of goods delayed);x_ijk: Binary decision variable (1 if mode k is selected from i to j; 0 otherwise);y_ij: Binary decision variable (1 if goods are transferred between i and j; 0 otherwise);

To facilitate model resolution, environmental benefits are quantified as carbon emission costs. The objective function integrates three components:transportation costs;time costs;carbon emission costs

\( {TC_{1}}=\sum _{i∈N,j∈N,k∈M}Q{c_{k}}{L_{ijk}}{x_{ijk}} \) (1)

\( {TC_{2}}=\sum _{i∈N,j∈N,k∈M}Qs_{k2}^{k1}{y_{ij}} \) (2)

\( {TC_{3}}=\sum _{i∈N,j∈N,k∈M}Q({T_{ij}}-{T_{ijk}}){W_{j}} \) (3)

\( {TC_{3}}=\sum _{i∈N,j∈N,k∈M}Q({T_{ijk}}-{T_{ij}})p \) (4)

\( {TC_{E}}=\sum _{i∈N,j∈N,k∈M}eQ{L_{ijk}}{e_{k}}{x_{ijk}}+\sum _{i∈N,j∈N,k∈M}eQe_{k2}^{k1}{y_{ij}} \) (5)

In Equation (1), TC₁ represents the transportation cost during transit;In Equation (2), TC₂ denotes the transfer cost during transportation;In Equation (3), TC₃ denotes the additional storage cost incurred during transportation when goods arrive early;In Equation (4), TC₃ represents the additional penalty cost incurred during transportation due to delayed arrival of goods.In Equation (5);TC_E represents the total carbon emission cost generated during the transportation process, which comprises two components:in-transit transportation carbon emission cost [9].

In Equation (6), it is explicitly constrained that each coal shipment from a source location to its destination must exclusively select a single transportation mode;In Equation (7), it is constrained that coal shipments at any node may either adopt a single transfer mode or undergo no transfer;In Equation (8) and Equation (9), coal transportation is restricted to the predefined set of available transportation and transfer modes, with the decision variables in this model formulated as binary (0-1) variables.

\( \sum {x_{ijk}}=1,∀i∈N,j∈N,k∈M \) (6)

\( {y_{ij}}≤1,∀i∈N,j∈N,i=j \) (7)

\( {x_{ijk}}∈\lbrace 0,1\rbrace ,∀i∈N,j∈N,k∈M \) (8)

\( {y_{ij}}∈\lbrace 0,1\rbrace ,∀i∈N,j∈N \) (9)

3. Algorithm design

In this study, the NSGA-II algorithm is employed for model resolution, with the specific implementation outlined as follows:Encoding and Initialization: A real-coded representation is adopted, where each chromosome is divided into two segments – path encoding and transportation mode encoding.Fitness Function: The fitness function integrates transportation cost, transportation time, and carbon emissions, with weight coefficients determined via the Analytic Hierarchy Process (AHP) [10].Non-dominated Sorting: A Pareto optimal solution set is constructed to prioritize non-dominated solutions while maintaining population diversity.Selection, Crossover, and Mutation: Tournament selection and path-specific mutation operators are applied to enhance genetic diversity within the population.Elitism Strategy: High-quality non-dominated individuals are preserved to accelerate convergence efficiency.This formulation ensures adherence to academic conventions, including passive voice, technical terminology precision, and structural clarity.

4. Model solving and analysis

4.1. Instance description

The adoption of containerized transportation for inland coal shipping represents a significant developmental trend. To enhance the practical relevance of this study, all data in this research are standardized using container units. This study employs 40-foot containers as the baseline unit, with a standardized payload of 30 tons per container.Figure 1 shows the simplified transportation network diagram

Figure 1: Multimodal transport network diagram

4.2. Data collection and processing

The railway unit freight rate is 1.85 yuan /TEU·km, and the water freight rate is 3.185 yuan /TEU·km. The average railway transport speed is 60km/h, and the unit carbon emission is 0.56kg/TEU·km. The average water transport speed is 30km/h, and the unit carbon emission is 1kg/TEU·km. The unit cost of converting the transportation mode between hot metal is 200 yuan /TEU, the unit transfer time is 0.08h/TEU, and the unit carbon emission is 1.92kg/TEU. Comprehensive different schemes, this paper uses 45 yuan/ton carbon dioxide emission tax rate for analysis.

4.3. Model solving analysis

Under deterministic conditions excluding uncertainty factors, the optimal route minimizing the combined transportation and carbon emission costs demonstrated operational metrics including transportation cost, carbon emission volume, carbon taxation expenditure, and transit duration, as detailed in Table 1.

Table 1: Cost, carbon emissions and transit time under optimal routes

For 30TEU coal shipments originating from Watang, the identified optimal logistics pathway involves rail transportation to Jining, followed by inland waterway shipping via the Beijing-Hangzhou Grand Canal, traversing strategic nodes including Xuzhou, Huaian, and Zhenjiang before final delivery to Shanghai.

Sensitivity Analysis Protocol: To verify the model's robustness and operational adaptability, this study conducted systematic sensitivity testing on critical parameters:Systematic parameter testing was conducted by adjusting rail freight rates to 0.35–3.35 yuan/TEU·km and waterway rates to 1.185–8.185 yuan/TEU·km. Subsequent observations quantified the resultant variations in transportation costs and carbon emission expenditures across these rate intervals, with parametric relationships graphically demonstrated in Figures 2 and 3.

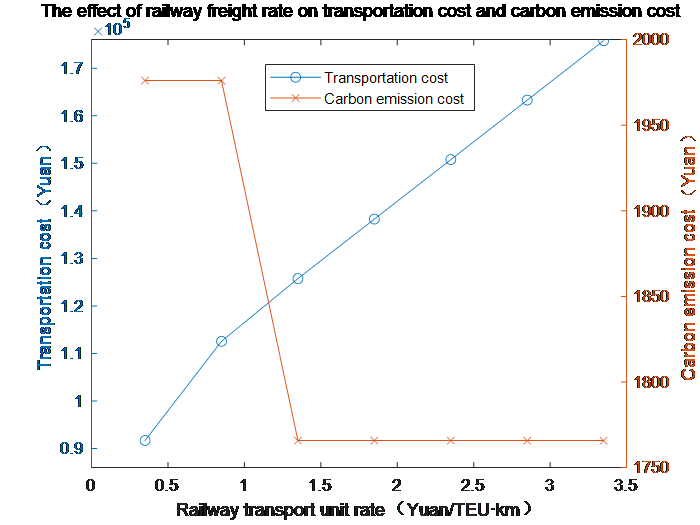
Figure 2: Sensitivity analysis diagram of railway unit rate

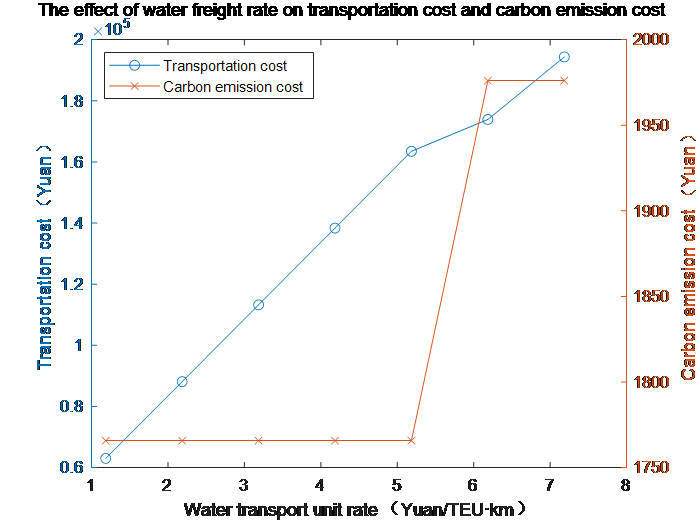
Figure 3: Sensitivity analysis diagram of waterway unit rate

The cost-effectiveness of coal transportation routes exhibits dynamic variations under different freight rate conditions. When railway rates fall below 1.35 yuan/TEU·km, Route 1T4W10 (via Wari Railway to Rizhao Port with maritime transfer) emerges as optimal. Conversely, above this threshold, Route 1T2W5W7W8W10 (rail-to-Jining followed by Beijing-Hangzhou Grand Canal inland waterway transit) becomes preferable. The canal route maintains cost superiority when waterway rates remain below 5.135 yuan/TEU·km, while maritime routing regains advantage beyond this critical value. Notably, despite Route 1T4W10's longer transportation distance and higher carbon emission costs under standard freight rates, its total costs remain lower than the canal alternative, demonstrating the comprehensive benefits of long-distance(intensive transportation) through optimized multimodal coordination. This cost paradox highlights the critical role of route-specific scale economies in intermodal transportation systems.

5. Conclusion

In this paper, the coal transportation route from Shanxi to Shanghai is optimized by constructing a multi-objective optimization model, considering transportation cost, carbon emission and transportation time. Studies have shown that railway and inland waterway transport have significant advantages in terms of cost and environmental benefits. The sensitivity analysis verifies the adaptability of the model, showing that the carbon tax rate has little effect on the total transportation cost, while the change of freight rate has a significant effect on route selection. This paper provides theoretical and practical reference for multimodal transport route optimization.