1. Introduction

In recent years the rapid expansion of the internet and social media has led to increased interest in the study of social networks [1-2]. Social networks not only capture the relationships between individuals but also reveal the underlying mechanisms of information dissemination and resource allocation. Among various network models the Erdos Renyi graph is notable for its simple structure and ease of analysis [3]. In this model any two nodes are connected with the same probability which, despite its simplicity, provides valuable insights into the fundamental structure and evolution of networks.

A key challenge in network analysis is recovering the underlying parameters that generate the network. In particular determining the connection probability from observed network data is of great practical significance. Maximum likelihood estimation is a well-established statistical method used to identify the parameter value that is most likely to have produced the observed data [4-6]. By constructing a likelihood function based on the edges present in a graph and then finding the parameter value that maximizes this function it is possible to obtain an estimate of the connection probability.

This paper provides a detailed discussion of the process of using maximum likelihood estimation to recover the connection probability in an Erdos Renyi graph. The estimated connection probability is then compared with the true probability used to generate the graphs. The results demonstrate that in dense networks the maximum likelihood estimator is highly effective while in sparse networks the estimates may be more sensitive to random variation though they still capture the overall network behavior.

The paper discusses some of the challenges that arise in practical applications. Real-world networks often display complex features such as community structures and heterogeneous node properties that are not captured by a single connection probability. In addition the computational demands of evaluating the likelihood function may increase significantly with the size of the network, making the method less feasible for very large networks. Future research should therefore focus on refining the estimation method or combining it with other statistical techniques to better handle complex network characteristics and large datasets.

The objective of this study is to validate the use of maximum likelihood estimation for accurately recovering the connection probability in Erdos Renyi graphs. By doing so the study not only contributes to the theoretical understanding of network parameter estimation but also provides practical insights that can be applied to both social network analysis and computer network design.

2. Theoretical foundations

2.1. Fundamentals of maximum likelihood estimation

MLE identifies parameter values that maximize the probability of observed data. For ER graphs, the likelihood function \( L(p) \) is derived from the binomial distribution of edges, where each edge exists independently with probability p. The log-likelihood is maximized to obtain the estimator:

\( p=Number of edges/C_{2}^{n} \) (1)

2.2. Overview of Erdős-Rényi graphs

An ER graph G (n, p) consists of n nodes connected randomly with probability p. Its adjacency matrix X is symmetric (for undirected graphs), with entries \( {X_{ij}}=1 \) if an edge exists between nodes i and j, and 0 otherwise. The model assumes homogeneity and independence, making it suitable for studying connectivity, clustering, and robustness.

3. Results

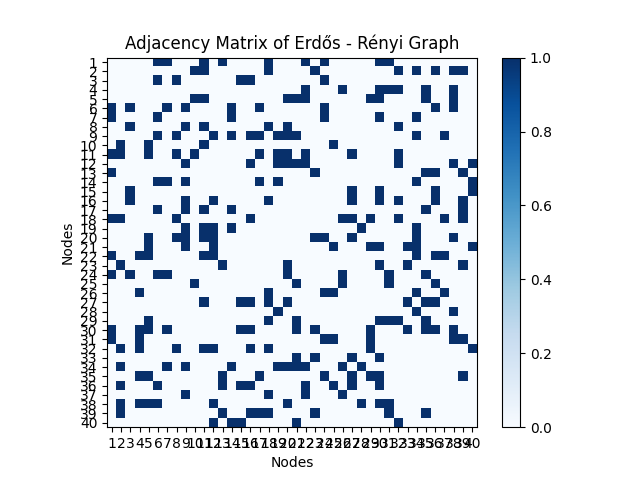
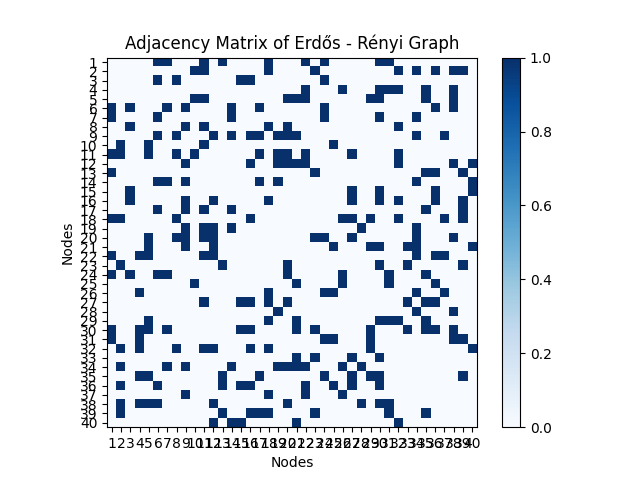
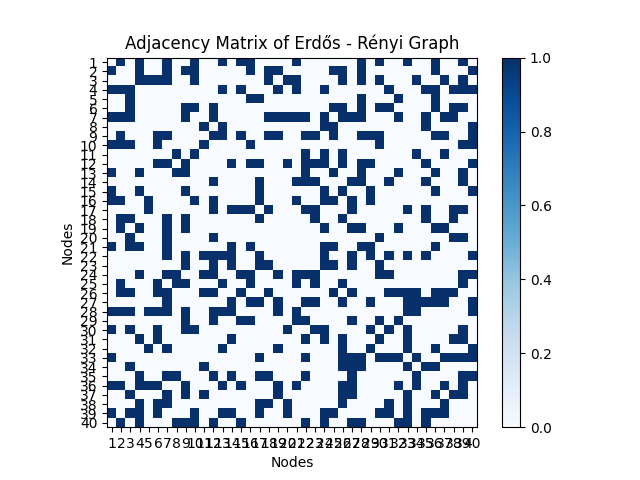
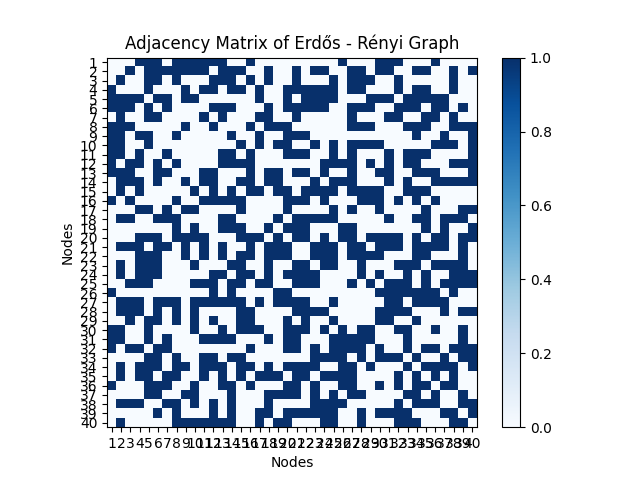
Data Generation: ER graphs with n=40 nodes were simulated for p in {0.1, 0.2, 0.3, 0.5}. Figure 1 shows the result.

MLE Implementation: The empirical \( \hat{p} \) was computed by dividing the observed edge count by \( C_{40}^{2}=780 \) .

Connectivity Trends: Higher p values yielded denser networks (e.g., p=0.5 produced 716 edges, p̂≈ 0.918.

Accuracy: Estimated \( \hat{p} \) closely matched true p, with minor deviations due to randomness (e.g., p=0.3 gave p̂≈0.2725).

Figure 1: The experiment result (picture credit: original)

4. Applications

The ability to accurately estimate the connection probability in an Erdos Renyi graph has a wide range of applications in both social and computer networks. In the realm of social networks, the application of maximum likelihood estimation to determine the parameter p plays a critical role in identifying influential nodes [7-8]. Social networks are dynamic systems where information, ideas, and trends spread through connections among individuals. By estimating the connection probability, analysts can better understand the underlying structure of these networks and identify nodes that serve as major conduits for information dissemination. For example, when a social network exhibits a high connection probability, the network is relatively dense and the influence of each node is more interconnected, meaning that a small change in the connectivity of one node can have a significant ripple effect across the entire network. In such cases, the ability to pinpoint influential nodes becomes essential for targeted marketing strategies, public health interventions, and political campaign planning.

The quantitative insights provided by maximum likelihood estimation facilitate the identification of clusters or communities within the larger network. Even though the Erdos Renyi model assumes a uniform probability for edge formation, deviations from the estimated value in localized regions may signal the presence of sub-communities or special groups [9]. These insights can be leveraged by social media platforms to enhance user engagement, by advertisers to target niche audiences, or by researchers studying the spread of information and misinformation. Additionally, knowing the estimated connection probability allows network analysts to simulate potential information cascades, model the diffusion of innovations, and design strategies to counteract the spread of harmful content.

In computer networks, the application of these techniques provides a foundation for modeling random topologies that are fundamental to the design and optimization of robust network infrastructures. Computer networks often require a balance between connectivity and resource allocation [10]. With the estimated value of p, network designers can simulate various scenarios to test the resilience of a network under different conditions. For instance, in scenarios where high connectivity is necessary for fault tolerance and data redundancy, a high value of p would suggest that the network is naturally robust. Conversely, if a network has a lower p value, it might indicate vulnerability to node or link failures, which could be critical for applications that require high reliability. The estimation of the connection probability thus informs decisions about where to add redundancy, how to distribute resources, and how to plan for contingencies in the event of component failures.

In the context of cloud computing and distributed systems, where resource allocation is a major concern, accurately modeling network topology with an estimated connection probability helps optimize performance and energy consumption. By simulating networks with different connectivity parameters, system architects can identify optimal configurations that reduce latency and improve overall throughput while minimizing costs. The insights gained from these simulations can be used to develop algorithms that dynamically adjust network parameters in response to changing load conditions or security threats, making real-time network optimization a possibility.

In addition to these applications, the estimated parameter p can serve as an initial condition or benchmark in more complex network models. For example, even though the Erdos Renyi graph model is relatively simple, it often forms the baseline from which more advanced models, such as scale-free networks or small-world networks, are developed. Researchers can use the estimated p to calibrate these models or to serve as a comparison metric when evaluating the performance of alternative modeling approaches. In essence, the ability to recover network parameters accurately using maximum likelihood estimation not only enhances the analysis of current networks but also contributes to the development of more sophisticated network models that can better capture the nuances of real-world connectivity.

5. Challenges

Despite the promising applications of maximum likelihood estimation in recovering the connection probability of Erdos Renyi graphs, several challenges remain that must be addressed for practical implementation. One of the primary issues is the inherent simplicity of the Erdos Renyi model. The assumption that every pair of nodes in the network has the same probability of being connected is a significant oversimplification of real-world networks. In actual social and computer networks, connections are often influenced by external factors such as geographic proximity, shared interests, or pre-existing relationships. This uniformity assumption means that while the Erdos Renyi model is mathematically tractable, it fails to capture critical features like community structures, node centrality variations, and preferential attachment. Consequently, the estimated parameter p may provide only a rough approximation of the underlying network structure, limiting the model’s effectiveness in predicting complex network behaviors.

Another challenge arises from the scalability of the maximum likelihood estimation method. As the number of nodes n in a network increases, the number of possible edges grows rapidly, following the combinatorial relationship \( n(n-1)/2 \) . For large networks, evaluating the likelihood function becomes computationally demanding, especially when dealing with massive datasets typical in modern social networks or large-scale computer networks. The computational burden associated with processing and optimizing the likelihood function may render the method impractical for very large networks unless significant computational resources or efficient algorithms are employed. Moreover, in networks where the number of nodes is vast, issues such as memory constraints and processing time become critical concerns, necessitating the development of scalable algorithms or approximation techniques that can handle large-scale estimation tasks without sacrificing accuracy.

Sparse networks pose an additional challenge for maximum likelihood estimation. When the connection probability p is very low, the resulting network tends to be sparse, and many nodes may be isolated or only weakly connected. In such cases, the number of observed edges is small relative to the total number of possible edges, leading to high variability in the estimation process. Random fluctuations can have a pronounced effect on the estimated value of p, making it less reliable as an indicator of the true network structure. This sensitivity to randomness in sparse networks complicates the analysis and may require the use of alternative statistical methods or regularization techniques to stabilize the estimation process [11]. Furthermore, sparse networks may be subject to sampling biases, where the observed data does not adequately represent the underlying connectivity due to missing or incomplete information. Addressing these issues requires robust estimation techniques that can account for data sparsity and provide reliable parameter estimates even in the presence of significant noise.

Beyond these technical challenges, the application of maximum likelihood estimation in real-world networks is further complicated by the dynamic and evolving nature of these networks. Social and computer networks are rarely static; they change over time as new nodes and edges are added or removed. The temporal dimension of network evolution introduces additional complexity into the estimation process, as the connection probability may vary over time. In dynamic networks, the estimation method must be adapted to account for time-varying parameters, which may involve developing time-series models or employing sequential estimation techniques that update the parameter estimates as new data becomes available. This dynamic aspect of networks further underscores the limitations of using a static model such as the Erdos Renyi graph for long-term network analysis.

6. Conclusion

In summary, this study has demonstrated that maximum likelihood estimation is a viable method for recovering the connection probability parameter in Erdos Renyi graphs. The ability to estimate p accurately is not only of theoretical interest but also has practical implications for the analysis and design of both social and computer networks. In social networks, the estimation of p provides valuable insights into network connectivity and facilitates the identification of influential nodes, thereby enhancing strategies for information dissemination and targeted marketing. In computer networks, the estimated parameter p informs the modeling of network topologies, contributing to the optimization of resource allocation, fault tolerance, and overall network robustness.

The challenges encountered in this study highlight the limitations of the Erdos Renyi model and the need for further research. The simplicity of the model, while beneficial for mathematical analysis, does not fully capture the complexities of real-world networks. This gap calls for the exploration of more sophisticated network models, such as stochastic block models or scale-free networks, which can account for community structures, heterogeneity among nodes, and preferential attachment mechanisms. Furthermore, the computational difficulties associated with scaling the maximum likelihood estimation method to large networks underscore the importance of developing efficient algorithms and approximation techniques.

Another critical aspect that emerged from this study is the sensitivity of the estimation process in sparse networks. As networks with low connection probabilities tend to be more susceptible to random fluctuations, future work should focus on enhancing the robustness of the estimation method in these settings. This may involve incorporating regularization techniques or leveraging alternative statistical frameworks, such as Bayesian inference, which can provide probabilistic estimates and quantify uncertainty in the parameter recovery process.

Several avenues for future research present themselves. One promising direction is the integration of dynamic network analysis with parameter estimation methods. Since most real-world networks are continuously evolving, developing models that can update parameter estimates in real time would significantly enhance the practical applicability of these techniques. Additionally, extending the current methodology to accommodate weighted networks, where connections have varying strengths, could provide a more nuanced understanding of network structure and dynamics.