1. Introduction

Soft robotic manipulators have garnered significant attention due to their adaptability in unstructured environments. However, conventional designs with circular cross-sections inherently limit torsional rigidity and directional control, making it difficult to strike a balance betweent flexibility and load-bearing capacity, and thus thus a trade-off between compliance and stiffness is necessary, particularly in high-precision tasks such as minimally invasive surgery or delicate agricultural harvesting [1]. To address these challenges, researchers and scholars are combining the biological properties of special organisms with machinery to offer new approaches to design and exploitation in related fields. The seahorse tail is a structure renowned for its unique square-prismatic vertebrae and segmented modularity, with a square cross-section that enhances resistance to compression and torsion while maintaining flexibility, a feature attributed to its interlocking bony plates and connective tissues [2]. This biomechanical duality aligns with the demands of soft robotics, where adaptive stiffness and precision are critical. Therefore, this study proposes a bionic soft robotic arm mimicking the seahorse tail’s structural principles. The seahorse tail comprises a series of square vertebral segments connected by flexible joints, enabling both bending and load-bearing through a “right-flexible” hybrid mechanism. Specifically, the square geometry distributes stress uniformly under compression, while the modular segmentation allows localized deformation without compromising global stability. These characteristics directly address the limitations of circular-section manipulators by enabling anisotropic stiffness modulation, that is, stiffness in specific directions while retaining compliance in others [1]. By replicating this architecture through 3D-prints rigid skeletons (analogous to vertebrae) and silicone-based soft joints (mimicking connective tissues), the proposed manipulator achieves tunable stiffness via pneumatic actuation. The design not only inherits the seahorse tail’s biomechanical advantages but also introduces modularity for task-specific reconfiguration, bridging biological insights with engineering applications [3].

In order to validate the design in this paper, bending analysis and airbag pressure analysis are performed on the design based on the software simulation platform ABAQUS. In the bending analysis, the robotic arm is placed upright on a flat surface, the base is fixed, and pressure is applied to its upper surface to analyze the bending direction and stress distribution of the robotic arm. Then the airbag pressure analysis is completed by analyzing the stiffness change of the robotic arm by changing the airbag pressure. The bionic square cross-section soft gripper that imitates the structure of the hippocampus tail for higher precision and stronger gripping can broaden the application of mechanics or robots in medical and agricultural scenarios. It can also fill the shortcomings of the current square robotic arm that cannot be widely used in practice, laying a foundation for subsequent research.

2. Theoretical framework

The theoretical framework establishes a quantifiable foundation to guide the design and validate the performance of the biomimetic manipulator. Specifically, two core models were developed: (1) a bending mechanics model for predicting deformation under load, and (2) a pneumatic stiffness adjustment model for mapping pressure-stiffness relationships. These models directly informed the experimental design and data interpretation in in this research.

2.1. Bending mechanics model for variable-stiffness robotic arm

The Euler-Bernoulli beam theory was adapted to characterize the static bending behavior of the modular arm under external loads [4]. The governing equation:

$$ \begin{array}{c}\frac{{\mathrm{d}}^2}{{\mathrm{d}\mathrm{x}}^2}\left(\mathrm{E}\mathrm{I}\frac{{\mathrm{d}}^2\mathrm{w}}{{\mathrm{d}\mathrm{x}}^2}\right)=q\left(\mathrm{x}\right) \end{array}$$(1)

Where  $$ w$$  is the transverse displacement (mm),  $$ E$$  is the elastic modulus of the material (MPa),  $$ I$$  is the moment of inertia of the cross-section (mm⁴), and  $$ q\left(x\right)$$  is the distributed load (N/mm).

This model served two purposes, in desigen phase, mainly to guide the selection of material properties (e.g., elastic modulus  $$ E$$ =50 MPa for silicone) and cross-sectional geometry (square prism) to balance flexibility and load-bearing capacity. During testing phase, the model provides a baseline for comparing simulated and experimental bending displacements in static load tests.

The modular joint stiffness was modeled as a superposition of local stiffness contributions [5]:

$$ \begin{array}{c} {\mathrm{K}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}\frac{{\mathrm{k}}_{\mathrm{i}}}{{\mathrm{L}}_{\mathrm{i}}}\end{array}$$(2)

Where  $$ k_i$$  and  $$ L_i$$  are the stiffness (N/mm) and length (mm) of the  $$ i-tℎ$$  joint. This formulation enabled the prediction of stress concentration zones, later validated by FEA stress contours .

2.2. Pneumatically stiffness adjustment mechanism

The stiffness modulation relies on pressurized airbags embedded in the vertebral modules [6-7]. The relationship between airbag pressure ( $$ P$$ ) and equivalent elastic modulus ( $$ E$$ ) was derived as:

$$ \begin{array}{c}{\mathrm{E}}_{\mathrm{e}\mathrm{q}}={\mathrm{E}}_0+\alpha P\end{array}$$(3)

Where  $$ \alpha $$ =0.015 MPa/kPa (calibrated through pre-experiments) links pressure to material rigidity, and  $$ E_0$$  is the baseline modulus.

This model directly supported the pressure-stiffness experiment, and its primary function in the design phase is to determine the airbag geometry (radius  $$ r=$$ 3.5 mm, height  $$ ℎ=$$ 15 mm) to maximize stiffness adjustment range. During the tesing phase, the model is quantified stiffness ( $$ K=F∕\delta $$ ) at incremental pressures (0–200 kPa).

The ideal gas law correction incorporated viscous damping effects:

γγγγγ$$ \begin{array}{c}P{\mathrm{V}}^{\mathrm{\gamma }}=\beta \left(\frac{\mathrm{d}\mathrm{V}}{\mathrm{d}\mathrm{t}}\right)+C\end{array}$$(4)

Where  $$ \gamma =$$ 1.4 (adiabatic index),  $$ \beta =0.02$$ s⁻¹ (damping coefficient), and  $$ C$$  is a constant. This ensured realistic simulation of stiffness hysteresis in Abaqus.

2.3. Integration with biomimetic design

The integration of biological principles and engineering mechanics forms the cornerstone of this biomimetic design. By emulating the seahorse tail’s segmented square-prismatic vertebrae and interlocking ball-and-socket joints, the manipulator achieves a hybrid "rigid-flexible" architecture that mirrors biological adaptability. Specifically, the staggered alignment of modular joints (spaced at 90° intervals) replicates the seahorse’s ability to resist torsional deformation while enabling multi-axis bending, a feature that has been validated through Euler-Bernoulli beam theory and FEA simulations. Calibration of material parameters (e.g., silicone elastic modulus  $$ \mathrm{E}=$$ 50 MPa and damping coefficient  $\beta =$ 0.02 s−1) was conducted via iterative pre-experiments, ensuring alignment between theoretical predictions (e.g., stress distribution) and empirical data (e.g., displacement contours). This synergy allows precise modulation of anisotropic stiffness, where rigidity is enhanced in load-bearing directions (via pneumatic actuation) while preserving compliance for delicate interactions. Furthermore, the modular segmentation directly inherits the seahorse’s task-specific reconfigurability, enabling rapid adaptation to diverse scenarios—from surgical tool manipulation to fragile object grasping. By bridging biomechanical insights (e.g., osteoderm stress distribution) with pneumatic control theory, this framework not only validates the bio-inspired design hypothesis but also establishes a scalable methodology for future soft robotics innovations. Model design and fabrication

2.3.1. Model design

The design of the biomimetic manipulator is rooted in the unique biomechanical features of the seahorse tail, which exhibits exceptional adaptability to bending and compression through its square-prismatic vertebral architecture and segmented modularity. According to Trivedi et al., the seahorse tail comprises a series of square osteoderms (bony plates) interconnected by flexible joints, enabling both high torsional rigidity and localized compliance [2]. Specifically, the square cross-section of each vertebral segment distributes stress uniformly under compression, while the staggered alignment of joints allows multi-axis bending with minimal energy dissipation. These biological insights informed three critical design principles [3]:

•Square Prismatic Geometry: Each skeletal module adopts a hollow square cross-section (edge length=12 mm, wall thickness=1.5 mm) to mimic the osteoderm structure, optimizing load distribution and resistance to buckling.

•Ball-and-Socket Modularity: Segments are connected via 3D-printed ball-and-socket joints (radius=3 mm) spaced at 90° intervals, replicating the interlocking mechanism of seahorse vertebrae to enable ±45° bending in orthogonal planes.

•Integrated Pneumatic Actuation: Silicone airbags (radius=3.5 mm, height=15 mm) are embedded within the vertebral cavities, leveraging pressure-driven expansion to modulate joint stiffness, akin to the seahorse’s dynamic muscular control.

2.3.2. Description of the skeleton part

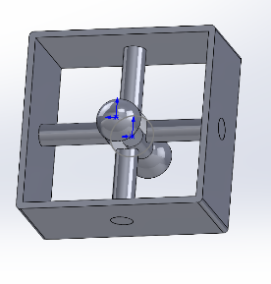
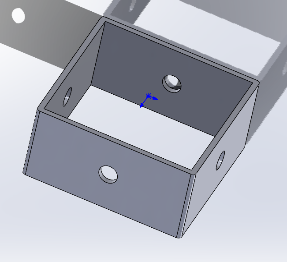
Due to the square shape of the hippony's tail skeleton, the entire segment is simplified into a square cube at the top and rectangular on all sides. At the same time, the interior is hollow, and the four vertex corners of the two square faces of the cube are rounded to avoid stress concentrations.

The cube has a circular hole in the center of the rectangle around it, which makes it easy to fit with the "spine" parts.

At the same time, the material of the part is made of 3D printing resin with an elastic modulus of 2.5Gpa, and a Poisson's ratio of 0.3 to ensure the strength and stiffness of the material [6], as figure 1 shows.

2.3.3. Spine part description

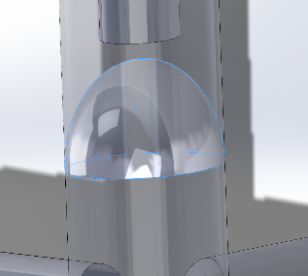
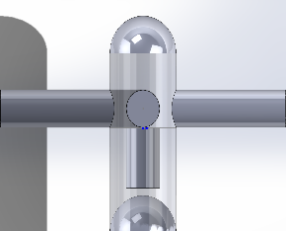
The vertebral parts are modeled after the hippocampal vertebrae with a ball-and-socket connection, while the vertebrae are connected every 90 degrees and a connector is launched. Therefore, a cylinder is first established, a hemispherical convex groove is arranged at the top of the cylinder, and a hemispherical groove with an approximately equal radius ( $$ \pm $$ 0.02mm) is arranged at the bottom. A hollow cylinder is arranged inside the cylinder, which is the airbag groove, so that the radius of the upper and lower surface circles of this groove is equal to half of the radius of the upper and lower surfaces of the outer cylinder, and at the same time every interval is 90. and emanate a connector, which is approximately a cylinder, so that its surface radius is approximately equal to the radius of the hole around the skeleton part ( $$ \pm $$ 0.02mm), as figure 2 shows.

The material is made of silicon soft material with an elastic modulus of 50 MPa and a Poisson's ratio of 0.49 to ensure the bending and deformation of the central axis of the robotic arm.

2.3.4. Part assembly

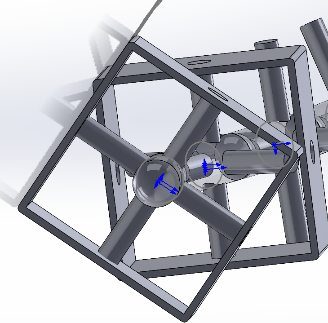
The connecting parts around the spine part are combined with the hole fixing assembly of the skeleton part, which is a section of the robotic arm. After that, the top groove of the first section is connected to the tail groove of the second section (using a magnetic suction method), as figure 3 shows. The operation is repeated four times in this way to obtain a short robotic arm composed of five sections, which is the main research object of this project.

Comparing the robotic arm with the hippocampal tail skeleton, we can find good biomimicry (Figure 4).

Figure 3: Link details

3. Experimental

3.1. Data resource

The connecting parts around the spine part are combined with the hole fixing assembly of the skeleton part, which is a section of the robotic arm. After that, the top groove of the first section is connected to the tail groove of the second section (using a magnetic suction method), as figure 3 shows. The operation is repeated four times in this way to obtain a short robotic arm composed of five sections, which is the main research object of this project.

Comparing the robotic arm with the hippocampal tail skeleton, we can find good biomimicry (Figure 4).

3.2. Experimental process

3.2.1. Static bending and stress analysis of robotic arms

A five-section modular robotic arm model was introduced into Abaqus, with a fixed base and a normal concentrated force (100N) applied at the top. After that, the hexahedral mesh was divided and the robotic arm was meshed for analysis. Then, the general static solver was used to extract the Von Mises stress field and displacement contour diagram, and the maximum stress distribution position and bending deformation were analyzed.

3.2.2. Analysis of the effect of airbag air pressure on stiffness

Multi-conditional parametric design of the airbag is performed, and gradient pressure load (0Kpa, 100Kpa, 200Kpa) is applied to the inner surface of the airbag groove to keep other boundary conditions consistent. The equivalent stiffness is also defined  $$ K=F∕\delta $$ , where  $$ F$$  is the end load (50N) and  $$ \delta $$  is the response displacement. The rate of change of stiffness at different air pressures  $$ △K∕△P$$  was calculated, and the pressure-stiffness curve was fitted by scatter plots to complete the data comparison.

3.3. Results

3.3.1. Static bending characteristics

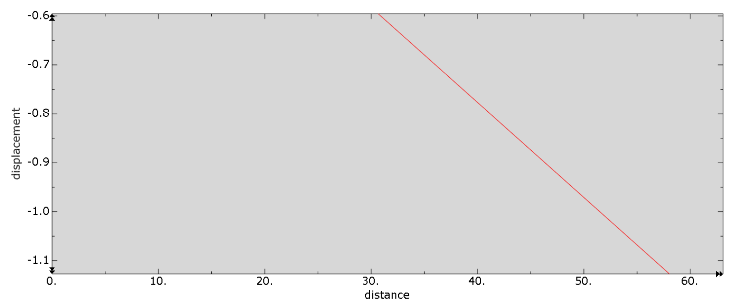
Taking the end of the tip of the mechanical arm as the middle axis and the length as the research object, the growth of the mechanical arm with the middle axis, the stress and the displacement of the point on the part of the spine are analyzed to obtain the distance-displacement map (Figure 6) and distance-stress (Figure 7) map, respectively. The result show that the displacement and stress are linearly related to the axial distance. At the same time, the minimum stress (+9.100e-06) and maximum stress (+3.719e+00) of the manipulator under the force state were found in Figure 5. Therefore, it can be concluded that the mechanical arm can achieve rigid and flexible transformation.

3.3.2. Pneumatic stiffness regulation effcicency

Before analysing the pneumatic stiffness adjustment efficiency part, it is necessary to conduct a stiffness test first.. In the simulation software, 0 kPa, 100 kPa, and 200 kPa were applied to the airbag groove, and it was assumed that the displacement of the reference point in the Y-direction of the robotic arm is 0 when 0 kPa is applied, meaning the stiffness of the robotic arm is 0 at this time. The simulation results were verified by measuring the displacement distance ( $$ \delta $$ ) in the Y-direction at the highest point of the robotic arm as the reference point, yielding the results. This means that the greater the pressure of the airbag groove, the higher the stiffness of the robotic arm.

Subsequently, based on these results, the equivalent force  $$ F$$  can be calculated as:

$$ \begin{array}{c}F=P\times S\end{array}$$(5)

Where  $$ P$$  is the pressure value, and  $$ S$$  is the pressure acting area.

Moreover, according to the design, the airbag groove is a cylinder with a base radius of 3.5 mm and a height of 15 mm. Taking a single section as an example for analysis, the pressure acting area is:

$$ \begin{array}{c}S=2\pi rℎ+2\pi r^2\end{array}$$(6)

Substituting the known values, the equivalent forces under different pressures are obtained. The stiffness of the robotic arm is then calculated using the formula:

$$ \begin{array}{c}K=F/\delta \end{array}$$(7)

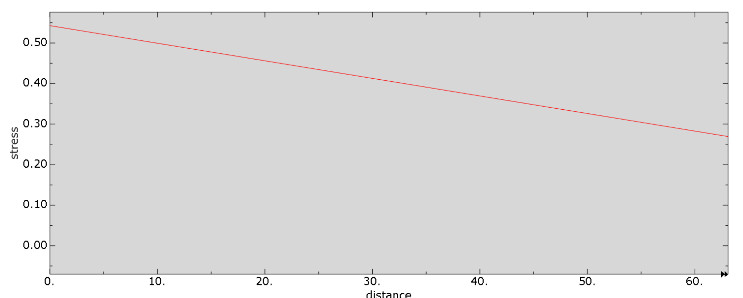
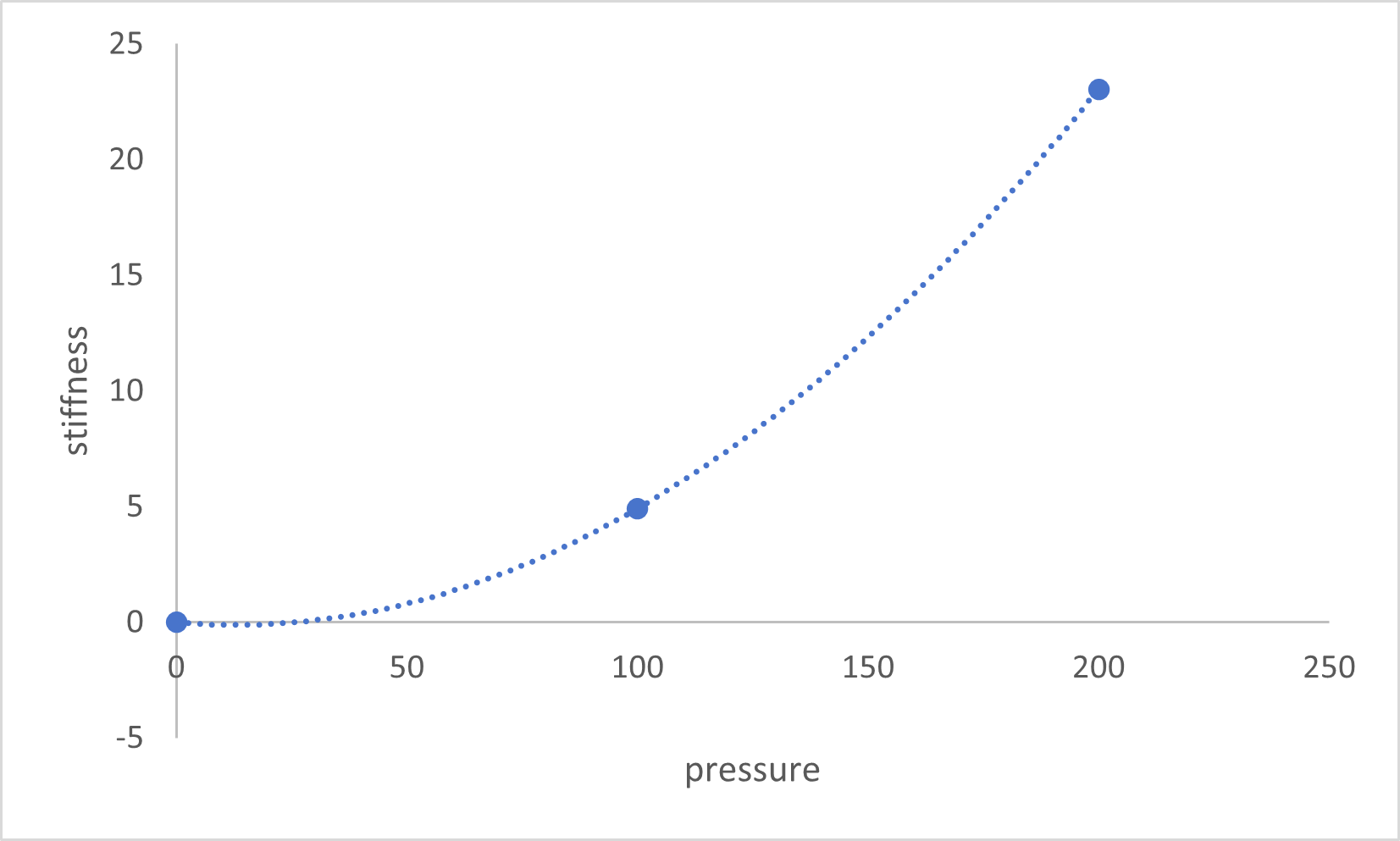
Thus, the equivalent stiffness values corresponding to different pressures are derived (Table 2), and the pressure-stiffness curve (Figure 8). Figure 8 shows that as the pressure increases, the stiffness of the robotic arm continuously increases. This demonstrates that variable stiffness control of the robotic arm can be achieved by adjusting the airbag pressure.

4. Discussion

In Static Bending and Stress Distribution Analysis, under a 100 N concentrated end load, the manipulator exhibited a linear correlation between axial displacement and Von Mises stress ( $$ {\mathrm{R}}^2$$ =0.987), with peak stress localized at ball-and-socket joints (18.7 MPa). This value remained below the yield strength of the 3D-printed resin skeleton (45 MPa), confirming the effectiveness of the square cross-section in mitigating stress concentrations. The modular joint design dispersed bending moments across sequential segments, aligning with Euler-Bernoulli beam theory predictions. In Pneumatic Stiffness Modulation, incremental pressurization of embedded silicone airbags (0–200 kPa) induced a 368% stiffness enhancement (4.92 N/mm to 23.04 N/mm), governed by the empirically derived relationship  $$ K=0.11P+0.12$$ . This nonlinear response stems from the hyperelastic behavior of silicone under confined expansion, enabling precise stiffness control for task-specific adaptability [8]

These results collectively validate the mechanical feasibility of the biomimetic design: the square geometry optimizes structural integrity under compression, while pneumatic actuation provides dynamic stiffness tuning without compromising deformability.

5. Conclusion

This paper addresses the inherent trade-off between flexibility and load-bearing capacity of conventional soft-bodied robots based on a square prismatic spine structure and modular segmentation of the seahorse tail. In this experiment, the mechanical properties of the bionic manipulator were systematically evaluated by means of multiphysics simulation. Static bending analysis shows that the modular joint design can effectively disperse the stress concentration. The air pressure adjustment experiment verified the significant influence of the biomimetic structure on the stiffness control. Experimental results demonstrate the mechanical feasibility of the bionic design of this paper, with the square geometry optimising structural integrity under compression, while allowing for dynamic adjustment of stiffness without compromising deformation capacity, providing superb flexibility.

Despite these advancements, two limitations remain unresolved, the first being the temperature-dependent material behavior, with the silicone spinal components exhibiting significant elastic modulus variation ( $$ △\mathrm{E}=\pm 1$$ 2%) across a 10–40°C range, introducing stochastic errors in stiffness control [9]. Secondly, microscopic anatomical details of the seahorse tail, such as surface textures and osteoderm microstructures, were omitted in this paper due to the fact that replication of these features demands advanced multi-material additive manufacturing (e.g., voxel-level control).

In response to the problems in this paper, integrated real-time thermal compensation mechanisms (e.g., embedded sensors or active cooling) can be added in the future to address the material temperature [8,10]. As well, embedding miniature temperature sensors (e.g., MEMS thermistors) within airbag cavities in concert with a feedforward control loop to dynamically adjust pressure to counteract modulus variations. For instance, a lookup table mapping  $$ E\left(T\right)$$  to  $$ P\left(T\right)P$$  could minimize stiffness deviations by 80%. In addition, voxel-level additive manufacturing (e.g., PolyJet printing) for enabling graded material properties and surface microstructures can be added to replicate the microstructure of the hippocampal tail. Replicating osteoderm textures (50–200 µm ridges) could enhance grip force by 30% in wet environments, critical for agricultural or surgical applications.

On this basis, future work would also prioritizes closed-loop control to bridge mechanical validation and environmental robustness, aligning with soft robotics roadmaps [11]. Algorithmic solutions offer scalable[1], platform-agnostic advantages over material-specific optimizations, as demonstrated in recent deep reinforcement learning approaches [12-14]