1. Introduction

Urban traffic congestion has become one of the major challenges in modern city management, which significantly reduces transportation efficiency and imposes severe environmental consequences. According to studies by the World Bank, urban traffic congestion results in annual economic loss of tens of billions of dollars.

Conventional signal controlling methods often use fixed-cycle signal, which lack the robustness and responsiveness needed to adapt to the dynamic traffic flows [1]. To cope with this defect, a variety of traffic signal optimization strategies are introduced to improve traffic system performances [2,3]. From the perspective of modeling approaches, the Nagel–Schreckenberg (NaSch) model, which is based on cellular automata, has been widely employed to simulate microscopic vehicle behaviors such as acceleration, deceleration and queuing along road segments and at intersections [4,5]. Many studies have extended traffic signal control this model to investigate how various signal strategies impact some metrics such as queue length and throughput [6,7]. Adaptive signal control systems such as SCOOT and SCATS have also been designed to improve the efficiency of traffic. These systems can adjust signal phases and green-light durations dynamically based real-time traffic conditions and is proven to be more effective than fixed-time control under realistic traffic conditions [8].

Another research direction centers on green wave control. This optimization strategy synchronizes traffic signals along arterial roads to decrease the stop frequency and thus curtail the travel time [9]. The drawback of this strategy lies in the fact that it usually demands relatively stable vehicle speeds and traffic densities; otherwise, its performance will deteriorate markedly. With the advancement of vehicle intelligence, intelligent green wave strategies using vehicle-to-everything (V2X) communication have been proposed in recent years. Systems such as Green Light Optimal Speed Advisory (GLOSA) guide vehicle speeds based on upcoming signal phases to reduce stopping [10]. Besides, multi-agent reinforcement learning methods are explored for signal control across multiple intersections, enabling decentralized agents to self-learn optimal coordination strategies by interacting with the traffic environment [11]. Although these approaches have demonstrated positive results on both isolated road segments and arterial roads, microscopic simulation studies integrating NaSch models with signal optimization remain relatively limited, especially in complex intersection scenarios involving signal-vehicle interactions.

This study aims to fill this gap by extending the signal-vehicle interactions to the classical NaSch model, so the main features of vehicles’ behavior due to signal light can be simulated. The research’s objective is to set up a model to describe the vehicle-signal interaction mechanism, assess the model’s capacity to represent signal-induced traffic behavior, and propose a signal optimization strategy based on the simulation results to enhance road utilization and vehicular efficiency.

The validation results demonstrate that the modified model is capable of reflecting the impact of signal timing on traffic behavior and is effective in evaluating the optimization of dynamic signal duration. This research broadens the applicability of microscopic traffic modeling and offers a novel perspective for intelligent traffic signal control. In terms of practical application, this research has the potential to alleviate congestion, enhance the commuting experience, and boost the development of intelligent and sustainable urban mobility systems.

2. Mathematical modeling of traffic flow

2.1. Microscopic model: NaSch model

In the Nagel-Schreckenberg model [4], a road is segmented and represented as a set of cells. In its original form, these cells are arranged in a single line with their two ends joined, forming a circular structure. Each cell is either an unoccupied section of the road or holds exactly one vehicle, meaning that no cell can be occupied by more than one car at any moment. Every vehicle has a velocity, which is an integer value ranging from 0 up to a maximum limit.

Time is divided into discrete intervals known as time steps. This division of both space and time gives rise to a cellular automaton. During each time step, the following four operations are executed in order, with each operation applied simultaneously to all vehicles:

Acceleration: Each vehicle increases its velocity by 1 unit, provided that this increase does not cause it to exceed the maximum velocity.

Deceleration: For each vehicle, the distance to the vehicle ahead (measured in cells) is compared with its current velocity (measured in cells per time step). If this distance is less than the current velocity, the vehicle’s velocity is adjusted down to the number of empty cells in front of it to prevent a collision.

3.Randomization: The speed of all cars that have a velocity of at least 1, is now reduced by one unit with a probability of p.

4.Car motion: All cars are moved forward the number of cells equal to their velocity so their positions are updated.

These four actions are repeated many times to simulate the traffic flow. The model simulates a single lane where cars cannot pass each other therefore there is no overtaking.

2.2. Model modification and optimization

Several structural modifications were made to the NaSch model for the purpose of simulating the vehicle - signal interaction. To be more specific, a deceleration mechanism was added for vehicles that are close to the intersection during red light phases, and during green light phases, a probabilistic model is introduced for each vehicle to either proceed straight through the intersection or decelerate and wait for the signal light. These modifications aim to simulate the real-world behavior of vehicles at urban signalized intersections more accurately. A more detailed description of these modifications is provided below.

2.2.1. Green light control logic

In real-world situations, vehicles approaching a green light will decide whether to accelerate or decelerate when the drivers see the number on the signal light depend on their distance to the intersection. Therefore a green light control logic is added in the model, which simulates this behavior with randomness. Some vehicles may accelerate when the countdown shows up, while others may decelerate to wait for the green signal in the next turn. The probability of accelerating or decelerating within a certain range is modeled using a linear relationship with respect to the distance to the intersection.

2.2.2. Red light control logic

During the red light phase, vehicles cannot pass through the intersection and will slow down or keep a lower speed due to the influence of the vehicle in front. Vehicles far from the intersection is not affected and continue to drive normally until they approach the intersection.

2.2.3. Other model modifications

In the classic NaSch model, a single lane forms a closed loop and the vehicles circulate. But in the modified model, in order to represent a road segment, the loop design is removed, with one end of the road being the entrance and the other end being the exit (which represents the intersection with traffic lights). The vehicle entry logic is also been modified. Instead of a continuous vehicle loop, the vehicle-entry mechanism is now based on a flow parameter that controls the probability of vehicle appearance. At the entrance, vehicles are randomly generated based on the calculated probability.

2.2.4. Explanations for modifications

Overall, these modifications are utilized to better simulate the behavior of vehicles under different traffic signals, thus investigating how the signal cycle (such as the green light duration and the red light duration) affects vehicle passage times and flow efficiency.

3. Traffic data analysis

In this model, the typical vehicle length is approximately 4.5 meters. Considering the spacing between vehicles, each cell is defined as 5 meters in length. A total of 100 cells are used to represent a 500-meter stretch of road leading up to the intersection. The simulation time step is set to be 1 second, which corresponds to the departure rate of approximately one vehicle per second at the intersection.

The maximum speed is set to 5 cells per second, corresponding to a realistic driving speed of 90 km/h. For simplicity, the red light duration is assumed to be 30 seconds longer than the green light, which means the green light time for the cross-direction is equal to the red light time for the current direction and the additional 30 seconds account for pedestrian crossing and turning vehicles.

To simulate the decisions of drivers near the end of the green phase, a probabilistic model is introduced for either rushing or waiting for the light during the final 5 seconds of the green signal. The probability of a vehicle choosing to wait is modeled as a linear function of its distance from the intersection at the fifth-to-last second. The probability takes value 0 at 75 meters and increases linearly to 1 at 125 meters.

Finally, the model simulates 15 hours of continuous traffic under identical conditions to reduce the effect of stochastic variability on average travel time.

4. The results of the study

When the traffic flow is relatively low so no congestion will occur, the travel time of vehicles that do not have to stop for traffic lights is not affected by the duration of the signal. However, the travel time of vehicles that wait for the signal is influenced by the duration of the red light, with waiting time increasing when the red light duration increases. The simulation results ( as shown in Fig. 1. ) indicate that the average travel time of vehicles shows a positive correlation with the duration of the red light, which aligns with the expected outcomes.

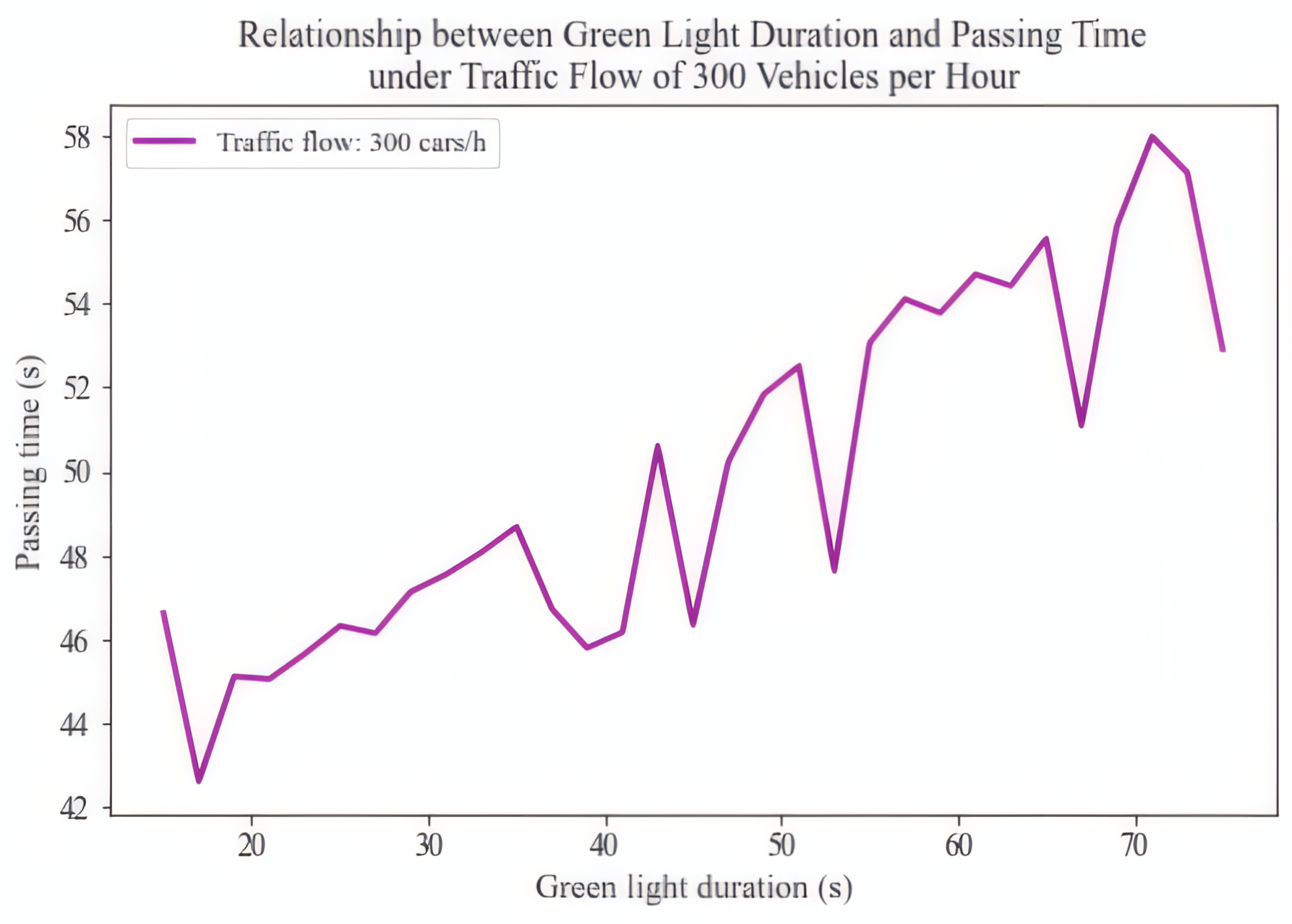
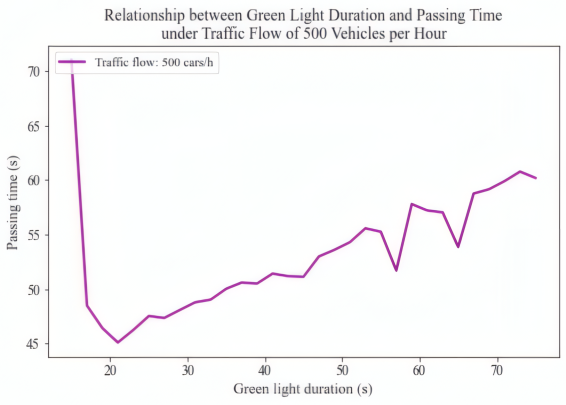
As traffic flow increases ( as shown in Fig. 2), the insufficient green light duration fails to meet the demand for vehicle passage, causing congestion at the intersection due to inadequate green light timing, which in turn prolongs the travel time. The simulation results indicate a negative correlation between the average travel time in the early stage and the green light duration, which also aligns with the expected outcomes.

This study finally investigates the relationship between travel time and hourly traffic flow volume by varying the traffic flow ( as shown in Fig. 3. ). As the flow increases, static green light durations lead to additional waiting times (as seen in the 45-second duration curve) or congestion (as observed in the 15-second duration curve). In comparison to fixed green light durations, dynamically controlling the traffic lights using optimized simulated times improves traffic flow efficiency by approximately 10%, reducing congestion and waiting times.

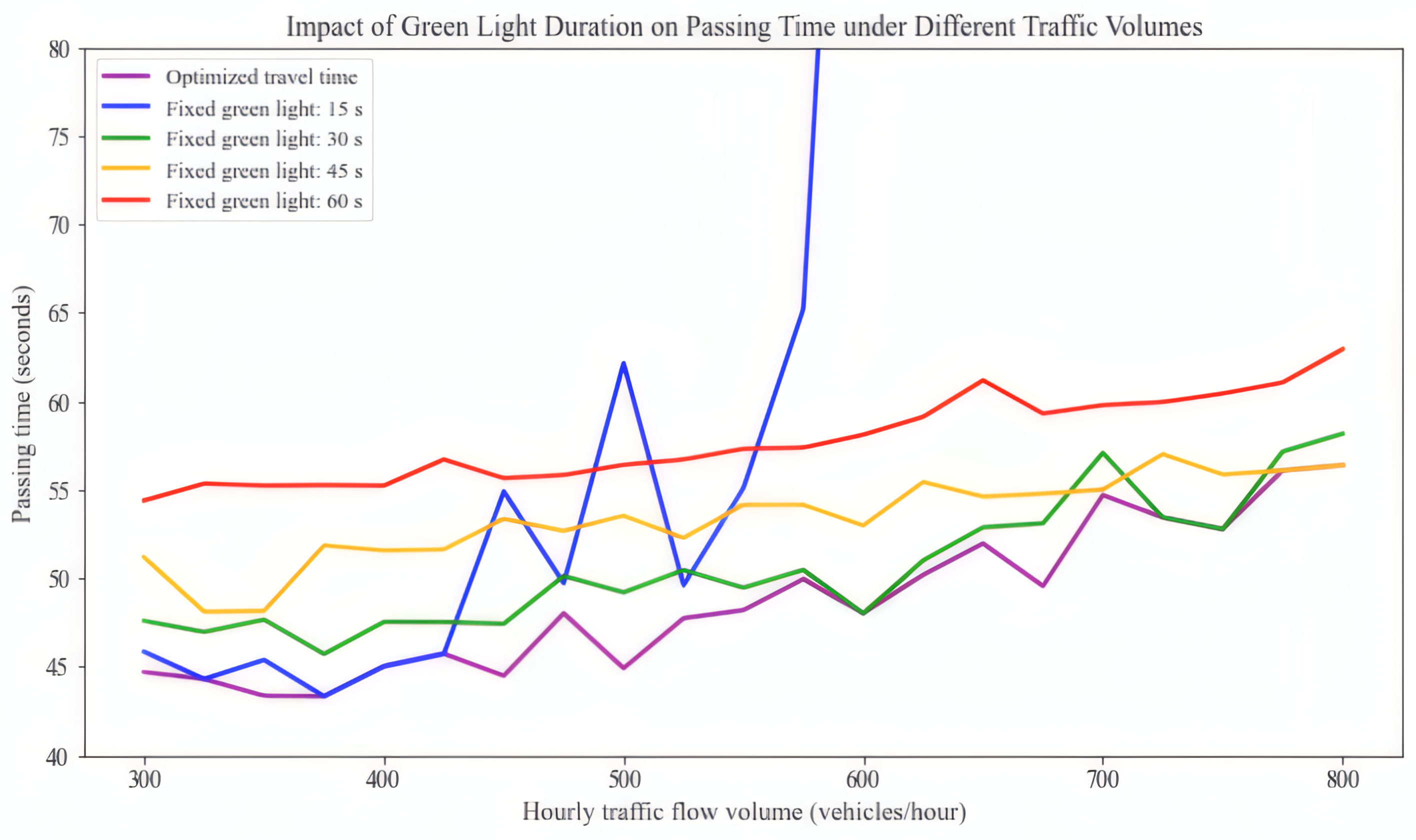
The simulation results confirm that the improved model effectively capture the influence of traffic signals on vehicles’ behavior and supports further evaluation of dynamic signal timing optimization.

5. Conclusion

This study improves the classical NaSch cellular automaton model by extending vehicle-signal interaction mechanism to analyze the relationship between traffic flow and travel time under various flow conditions. Simulation results demonstrate that the NaSch-based vehicle-signal interaction model exhibits robust performance across different traffic volumes. Moreover, dynamic signal control using optimized green light durations improves traffic efficiency by approximately 10%, which significantly reduces waiting times for vehicles and mitigates congestion compared to fixed-timing strategies.

Due to computational constraints and model simplification, the current implementation of this model simulates single-lane traffic, which deviates from real-world multi-lane road systems. Future work could incorporate lane-changing mechanisms and lateral traffic flows as this model has a good extensibility. Therefore, more fine-grained simulations can be made and directional imbalances between main and secondary roads can be presented.The red light timing estimation, which is constrained by computational limitations, could also be improved with higher-fidelity simulations.

Beyond structural improvements to the model, future directions may involve interfacing with map APIs to obtain real-time traffic data, which enables adaptive signal timing in real-world scenarios. Integrating deep - learning techniques into this model along with real - world data may further improve traffic flow prediction. As autonomous vehicles and traffic digitization become more prevalent, the rationality and predictability of vehicular behavior will improve, and so will the accuracy of the extended model. With proper privacy safeguards, vehicle-to-everything (V2X) communication can be incorporated in the future to enable more intelligent and cooperative signal control, further enhancing the traffic flow efficiency.