1. Introduction

The coronary arteries, which encircling the heart, are critical vessels tasked with supplying oxygenated blood to cardiac tissues. They primarily consist of the left coronary artery (further branching into the anterior descending and left circumflex arteries) and the right coronary artery. Given the exceptionally high metabolic activity of myocardial tissues and their heavy reliance on oxygen, maintaining uninterrupted coronary blood flow is essential for sustaining the heart’s pumping functionality. The development of atherosclerosis, stenosis, or occlusion can trigger severe cardiovascular events such as angina pectoris or myocardial infarction [1]. Despite notable advancements in anatomical imaging diagnostics, detecting early-stage functional abnormalities in coronary arteries remains challenging. This difficulty arises from the inherently nonlinear and dynamically coupled characteristics of the vascular system under physiological conditions, which traditional static metrics fail to adequately capture [2]. Consequently, developing mathematical models of vascular dynamics grounded in nonlinear dynamical theory holds significant promise for elucidating the mechanisms underlying coronary artery disease, predicting potential pathological risks, and guiding effective interventions [3].

2. Literature review

Georg Duffing introduced the Duffing equation in 1918, defining nonlinear dynamics and chaos theory. Its applications include mechanical, electronic, and biological systems. Wiggins expanded on it in 1987. In 2002, Flaviano Battelli and Michal Fečkan explored the conditions governing the vanishing and non-vanishing of Melnikov functions under perturbations, introducing higher-order Melnikov methods for detailed chaotic condition analysis [4]. In 2012, Anjali Sharma and colleagues systematically examined the effects of nonlinear damping on bifurcation and chaos in forced Duffing oscillators, using Melnikov methods combined with Lyapunov exponent calculations, and demonstrated that higher-order nonlinear damping significantly lowered the chaos threshold while expanding unstable regions [5]. Given the pronounced elasticity of vascular tissues, the Duffing equation has also been applied to vascular dynamics research. George Austin, in 1971, initially employed the Duffing equation to model aneurysm hemodynamics and pressure fluctuations within the Circle of Willis, showing potential chaotic behavior under heightened pulsatile pressures [6]. Nonetheless, early model simplified nonlinear restoring forces, but later developed Van der Pol-Duffing cerebrovascular dynamics model, integrating vascular elasticity, blood rheology, and pressure dynamics for early cerebral aneurysm diagnosis [7]. In 2019, D.W. Qian and Y.F. Xi viewed coronary artery spasms as chaotic processes, proposing a sliding mode control strategy for achieving chaos synchronization, demonstrating robust performance under uncertain disturbances [8]. More recently, in 2025, Wenxin Zhang and Lijun Pei established nonlinear Duffing-based models for N-type and S-type muscular blood vessels, examining bifurcation and chaos phenomena under periodic perturbations using multi-scale analysis methods. Although these models showed strong applicability for capturing vascular dynamics, there remains room for enhancing the description of complex physiological perturbations [9]. This study uses the Duffing equation to construct a dynamic model of coronary artery behavior, aiming to understand oscillations, loss of stability, and chaotic phenomena, improving risk prediction strategies [10].

3. Mathematical modeling of coronary artery equation

The mathematical modeling of coronary artery equations is essential for understanding the behavior of the arterial system under various conditions. This section presents the formulation of the N-type and S-type equations that describe the dynamics of the coronary arteries.

3.1. N-type equation and S-type equation

N-type and S-type vascular models are important theoretical frameworks for studying the nonlinear dynamic behavior of blood vessels. N-type blood vessels usually exhibit negative stiffness, and their pressure-diameter relationship tends to soften in a certain interval, resulting in increased sensitivity to external perturbations. In contrast, S-type vessels have typical S-shaped pressure-diameter curves, which contain both stiffened and softened zones, with a higher degree of nonlinearity, and are prone to multi-stability and complex kinetic responses. Mathematically, these two types of models are often described by introducing higher-order nonlinear terms to describe the wall stress-strain relationship and adding viscous damping and cyclic driving to the equations to simulate pulsatile blood flow. In recent years, approximate models based on Duffing's equation have been widely used to analyze the stability, limit rings, and chaotic behaviors of N-type and S-type blood vessels, providing an important theoretical basis for understanding the mechanisms of cardiovascular diseases.

3.1.1. N-type equation

The N-type equation is a nonlinear differential equation that captures the dynamics of blood flow and pressure in the coronary arteries. It is given by:

$$$ \begin{array}{c}\frac{{\mathrm{d}}^2\mathrm{x}}{\mathrm{d}{\mathrm{t}}^2}+\alpha \frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}}+\beta x=\gamma \sin \left(\mathrm{\omega }\mathrm{t}\right)\end{array}$$$(1)

Where  $$ \mathrm{x}$$  represents the arterial displacement,  $$ \mathrm{\alpha },\mathrm{ }\mathrm{\beta }$$ , and  $$ \mathrm{\gamma }$$  are constants, and  $$ \mathrm{\omega }$$  is the frequency of the oscillating input. This equation models the oscillations and damping characteristics of the coronary artery under periodic excitation.

3.1.2. S-type equation

The S-type equation is another form of the equation used to model coronary artery dynamics, characterized by a different nonlinear relationship between pressure and blood flow. It can be written as:

$$$ \begin{array}{c}\frac{{\mathrm{d}}^2\mathrm{y}}{\mathrm{d}{\mathrm{t}}^2}+\delta \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}+ϵ{\mathrm{y}}^3=\eta \cos \left(\mathrm{\zeta }\mathrm{t}\right)\end{array}$$$(2)

Here, y presents the displacement in the S-type model, and  $$ \mathrm{\delta },\mathrm{ }\mathrm{ }\mathrm{ϵ},\mathrm{ }\mathrm{ }\mathrm{\eta }$$  and  $$ \mathrm{\zeta }$$  are constants. This model emphasizes and the nonlinear damping and the cubic dependence of the displacement on the velocity.

3.2. Chaos system analysis

The chaotic behavior of coronary arteries can be analyzed using various dynamical system techniques, including the Hamiltonian approach, Melnikov function, and the study of the chaotic conditions for both the N-type and S-type equations.

3.2.1. Hamiltonian function analysis

The Hamiltonian function is a key tool for studying the dynamics of chaotic systems. For both the N-type and S-type equations, the Hamiltonian can be expressed as

$$$ \begin{array}{c}H\left(\mathrm{x},\dot{\mathrm{x}}\right)=\frac{1}{2}m{\dot{\mathrm{x}}}^2+\frac{1}{2}k{\mathrm{x}}^2\end{array}$$$(3)

Where  $$ \mathrm{x}$$  represents the displacement and  $$ \dot{\mathrm{x}}$$  the velocity. The phase space of the N-type and S-type equations, when plotted along with the stable and unstable manifolds, reveals the dynamics of these systems.

3.2.2. Melnikov function

The Melnikov function is used to assess the possibility of chaos in dynamical systems. It measures the distance between stable and unstable manifolds of a system, providing insight into the system’s chaotic behavior. For both the N-type and S-type equations, the Melnikov function can be derived as:

$$$ \begin{array}{c}M\left(\mathrm{\alpha }\right)= {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin \left(\mathrm{\alpha }\mathrm{t}\right)\mathcal{ℱ}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}\end{array}$$$(4)

Where  $$ \mathcal{ℱ}\left(\mathrm{t}\right)$$  is a forcing term that represents external influences on the system, The Melnikov function helps identify the conditions under which chaos arises in the coronary artery models.

3.2.3. Chaos conditions for N-type and S-type equations

For the N-type and S-type equations to exhibit chaotic behavior, certain conditions must be satisfied. These conditions involve the interaction between the nonlinear terms and the external forcing terms, as well as the presence of sensitive dependence on initial conditions. The conditions for chaos can be determined by analyzing the bifurcation diagrams and Lyapunov exponents of the system.

4. Analysis of N-type coronary vessels under small perturbations

To systematically analyze and unify the nonlinear behaviors observed in coronary artery models, we introduce a generalized two-dimensional coupled dynamical system. This formulation serves as a universal framework from which both the N-type and S-type systems can be derived as special case by choosing appropriate parameter values.

4.1. Mathematical formulation

We defined the generalized coupled nonlinear system as follows:

$$$ \begin{array}{c}\{\begin{array}{c}\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{\tau }}=\lambda [{\mathrm{\mu }}_{1}y+{\mathrm{\mu }}_{2}x+{\mathrm{\mu }}_3{\mathrm{x}}^3+{\mathrm{\mu }}_4{\mathrm{y}}^3+{\mathrm{\mu }}_5\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{\tau }}]\\ \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{\tau }}=-ax-by\end{array} \end{array}$$$(5)

In this model,  $$ \mathrm{x}\left(\mathrm{\tau }\right)$$  and  $$ \mathrm{y}\left(\mathrm{\tau }\right)$$  denote the dynamic state variables associated with arterial wall displacement and flowrelated quantities, respectively, with τ the normalized (dimensionless) time;  $$ \mathrm{\lambda }$$  is a global scaling factor that sets the overall coupling strength;  $$ \mathrm{a},\mathrm{b}>0$$  are damping parameters governing the decay of  $$ \mathrm{y}\left(\mathrm{\tau }\right)\mathrm{ }$$ through wall resistance and bloodflow dissipation;  $$ {\mathrm{\mu }}_1\mathrm{ }$$ provides linear coupling from  $$ \mathrm{y}$$  to  $$ \mathrm{x}$$ , representing direct wall–flow interaction;  $$ {\mathrm{\mu }}_2\mathrm{ }$$ gives linear selffeedback of  $$ \mathrm{x}$$  corresponding to elastic wall recoil;  $$ {\mathrm{\mu }}_3\mathrm{ }$$ adds nonlinear selffeedback of  $$ \mathrm{x}$$ , capturing elastic saturation or stiffening;  $$ {\mathrm{\mu }}_4\mathrm{ }$$ introduces a cubic nonlinearity in  $$ \mathrm{y}$$  that models flowinduced nonlinear feedback; and  $$ {\mathrm{\mu }}_5$$  supplies derivative coupling through  $$ \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{\tau }}$$ , allowing delayed feedback or viscoelastic memory effects. This unified formulation accommodates multiple physical mechanisms and nonlinear structures via parameter selection: choosing  $$ {\mathrm{\mu }}_3=0$$  with  $$ {\mathrm{\mu }}_4\ne 0$$  yields dynamics whose nonlinearity is dominated by the flow variable  $$ \mathrm{y}$$ , characteristic of an Ntype system; selecting  $$ {\mathrm{\mu }}_3\ne 0$$  with  $$ {\mathrm{\mu }}_4=0$$  concentrates the nonlinear effects in the walldisplacement variable  $$ \mathrm{x}$$ , representative of an Stype system; and taking  $$ {\mathrm{\mu }}_5\ne 0\mathrm{ }$$ renders the system nonconservative, enriching its dynamics with delayinduced instabilities and the possibility of chaotic behavior.

This generalized form provides several key advantages:

1. Model Unification: Both N-type and S-type models are recoverable by parameter specification, facilitating a direct comparative study.

2. Analytical Tractability: The model can be reduced to a second-order differential equation (ODE) via substitution, making it suitable for Melnikov analysis and Hamiltonian structure investigation.

3. Parametric Flexibility: Smooth interpolation between model types enables parameter continuation studies, bifurcation tracking and chaos boundary identification.

In the following subsections, we will show how specific parameter configurations yield the canonical N-type and S-type equations, and how their dynamical behaviors diverge under perturbations.

4.2. N-type system melnikov function

The perturbed second-order form of the N-type system is:

$$$ \begin{array}{c}\frac{{\mathrm{d}}^2\mathrm{y}}{\mathrm{d}{\mathrm{\tau }}^2}=-b\left\{\mathrm{\lambda }\left[-\left(1+\mathrm{b}\right)\mathrm{x}+{\mathrm{y}}^3-\left(1+\mathrm{c}\right)\mathrm{y}\right]+{\mathrm{ϵ}}_1\frac{1}{{\left(\mathrm{y}+\mathrm{\delta }\right)}^{\mathrm{n}}}+{\mathrm{ϵ}}_3\sin \left(\mathrm{\omega }\mathrm{x}\right)\right\}-c\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{\tau }}-{\mathrm{ϵ}}_2\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{\tau }}\bullet \frac{\mathrm{d}}{\mathrm{d}\mathrm{y}}\left[\tanh \left(\mathrm{k}\mathrm{y}\right){\left|\mathrm{y}\right|}^{\mathrm{\gamma }}\right]\end{array}$$$(6)

The unperturbed system (setting  $$ {\mathrm{ϵ}}_1={\mathrm{ϵ}}_2={\mathrm{ϵ}}_3=0$$ ) becomes:

$$$ \begin{array}{c}\ddot{\mathrm{y}}+ay-b{\mathrm{y}}^3=0\end{array}$$$(7)

With Hamiltonian:

$$$ \begin{array}{c}{\mathrm{H}}_{\mathrm{N}}\left(\mathrm{y},\dot{\mathrm{y}}\right)=\frac{1}{2}{\dot{\mathrm{y}}}^2+\frac{\mathrm{a}}{2}{\mathrm{y}}^2-\frac{\mathrm{b}}{4}{\mathrm{y}}^4\end{array}$$$(8)

Let  $$ ({\mathrm{y}}_0\left(\mathrm{\tau }\right),\mathrm{ }\dot{{\mathrm{y}}_0\left(\mathrm{\tau }\right))}$$  be the homoclinic orbit of the unperturbed system. The Melnikov function is then:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{N}}\left({\mathrm{t}}_0\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left[\left(-\mathrm{a}{\mathrm{y}}_0+\mathrm{b}{\mathrm{y}}_0^3\right)\bullet \left(-\mathrm{b}{\mathrm{ϵ}}_1\frac{1}{{\left(\mathrm{y}+\mathrm{\delta }\right)}^{\mathrm{n}}}-\mathrm{b}{\mathrm{ϵ}}_3\sin \left(\mathrm{\omega }\mathrm{x}\left({\mathrm{y}}_0,\mathrm{ }\dot{{\mathrm{y}}_0}\right)\right)\right)+\dot{{\mathrm{y}}_0}\bullet \left(-\dot{{\mathrm{y}}_0}-{\mathrm{ϵ}}_2\frac{\mathrm{d}}{\mathrm{d}\mathrm{\tau }}\left[\tanh \left(\mathrm{k}{\mathrm{y}}_0\right){\left|{\mathrm{y}}_0\right|}^{\mathrm{\gamma }}\right]\right)\right]\mathrm{d}\mathrm{\tau }\end{array}$$$(9)

Thus, the Melnikov function becomes:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{N}}\left({\mathrm{t}}_0\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left[\begin{array}{c}\left(-\mathrm{a}{\mathrm{y}}_0+\mathrm{b}{\mathrm{y}}_0^3\right)\bullet \left(-\mathrm{b}{\mathrm{ϵ}}_1\frac{1}{{\left(\mathrm{y}+\mathrm{\delta }\right)}^{\mathrm{n}}}-\mathrm{b}{\mathrm{ϵ}}_3\sin \left(\mathrm{\omega }\mathrm{x}\left({\mathrm{y}}_0,\mathrm{ }\dot{{\mathrm{y}}_0}\right)\right)\right)\\ -c{\dot{{\mathrm{y}}_0}}^2-{\mathrm{ϵ}}_2{\dot{{\mathrm{y}}_0}}^2\left(\mathrm{k}{\mathrm{sech}\left(\mathrm{k}{\mathrm{y}}_0\right)}^2{\left|{\mathrm{y}}_0\right|}^{\mathrm{\gamma }}+\tanh \left(\mathrm{k}{\mathrm{y}}_0\right)\bullet \mathrm{\gamma }{\left|{\mathrm{y}}_0\right|}^{\mathrm{\gamma }-1}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathrm{y}}_0\right)\right)\end{array}\right]\mathrm{d}\mathrm{\tau }\end{array}$$$(9)

This expression captures all perturbation contributions, including Linear damping  $$ -\mathrm{c}{\dot{{\mathrm{y}}_0}}^2$$ , Threshold-type damping via tanh, Singular forcing via  $$ \frac{1}{{\left(\mathrm{y}+\mathrm{\delta }\right)}^{\mathrm{n}}}$$ , Periodic excitation via  $$ \sin \left(\mathrm{\omega }\mathrm{x}\right)$$ . It provides a complete basis for analyzing homoclinic orbit splitting and the onset of chaos.

We express the Melnikov function as:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{N}}\left({\mathrm{t}}_0\right)={\mathrm{M}}_{\mathrm{N}}^0+{\mathrm{ϵ}}_3{\mathrm{R}}_{\mathrm{N}}\cos \left(\mathrm{\omega }{\mathrm{t}}_0+\mathrm{\varphi }\right)\end{array}$$$(10)

Where the non-periodic component is given by:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{N}}^0={\mathrm{M}}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}}^{\mathrm{N}}+{{\mathrm{M}}_{\mathrm{d}\mathrm{a}\mathrm{m}\mathrm{p}}^{\mathrm{N}}+\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{\mathrm{N}}\end{array}$$$(11)

With:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}}^{\mathrm{N}}=b{\mathrm{ϵ}}_1{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(\mathrm{a}{\mathrm{y}}_0-\mathrm{b}{\mathrm{y}}_0^3\right)\bullet \frac{1}{{\left(\mathrm{y}+\mathrm{\delta }\right)}^{\mathrm{n}}}\mathrm{d}\mathrm{\tau }\end{array}$$$(12)

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{d}\mathrm{a}\mathrm{m}\mathrm{p}}^{\mathrm{N}}=-c{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\dot{{\mathrm{y}}_0}}^2\mathrm{d}\mathrm{\tau }\end{array}$$$(13)

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{\mathrm{N}}=-{\mathrm{ϵ}}_2{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\dot{{\mathrm{y}}_0}}^2\bullet \left(\mathrm{k}{\mathrm{sech}\left(\mathrm{k}{\mathrm{y}}_0\right)}^2{\left|\mathrm{y}\right|}^{\mathrm{\gamma }}+\tanh \left(\mathrm{k}{\mathrm{y}}_0\right)\bullet \mathrm{\gamma }{\left|{\mathrm{y}}_0\right|}^{\mathrm{\gamma }-1}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathrm{y}}_0\right)\right)\mathrm{d}\mathrm{\tau } \end{array}$$$(14)

The periodic component is described via:

$$$ \begin{array}{c}{\mathrm{C}}_1^{\mathrm{N}}=-b{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(\mathrm{a}{\mathrm{y}}_0-\mathrm{b}{\mathrm{y}}_0^3\right)\bullet \sin \left(\mathrm{\omega }{\mathrm{x}}_0\left(\mathrm{\tau }\right)\right)\cos \left(\mathrm{\omega }\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }\end{array}$$$(15)

$$$ \begin{array}{c}{\mathrm{C}}_2^{\mathrm{N}}=-b{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(\mathrm{a}{\mathrm{y}}_0-\mathrm{b}{\mathrm{y}}_0^3\right)\bullet \sin \left(\mathrm{\omega }{\mathrm{x}}_0\left(\mathrm{\tau }\right)\right)\sin \left(\mathrm{\omega }\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }\end{array}$$$(16)

$$$ {\mathrm{R}}_{\mathrm{N}}=\sqrt{{{(\mathrm{C}}_1^{\mathrm{N}})}^2+{\left({\mathrm{C}}_2^{\mathrm{N}}\right)}^2},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{\varphi }=\arctan \left(\frac{{\mathrm{C}}_2^{\mathrm{N}}}{{\mathrm{C}}_1^{\mathrm{N}}}\right)$$$

4.3. N-type chaos criterion

The sufficient condition for homoclinic chaos is now expressed as:

$$$ \begin{array}{c}\left|{\mathrm{M}}_{\mathrm{N}}^0\left({\mathrm{ϵ}}_1+{\mathrm{ϵ}}_2\right)\right|<{\mathrm{ϵ}}_3{\mathrm{R}}_{\mathrm{N}}\end{array}$$$(17)

Here:

 $$ {\mathrm{M}}_{\mathrm{N}}^0$$  is the non-periodic contribution to the Melnikov function, explicitly dependent on  $$ {\mathrm{ϵ}}_1$$  and  $$ {\mathrm{ϵ}}_2$$ .

 $$ {\mathrm{ϵ}}_3\mathrm{R}$$  is the amplitude of the periodic component, modulating the sinusoidal perturbation strength.

This inequality ensures that the Melnikov function $$ {\mathrm{ }\mathrm{M}}_{\mathrm{N}}\left({\mathrm{t}}_0\right)$$  has a simple zero in  $$ {\mathrm{t}}_0$$ , indicating transverse intersection of stable and unstable manifolds, and hence chaotic behavior\

This formulation emphasizes the “interplay of different types of perturbations” in the onset of chaos and facilitates parameter-based bifurcation analysis.

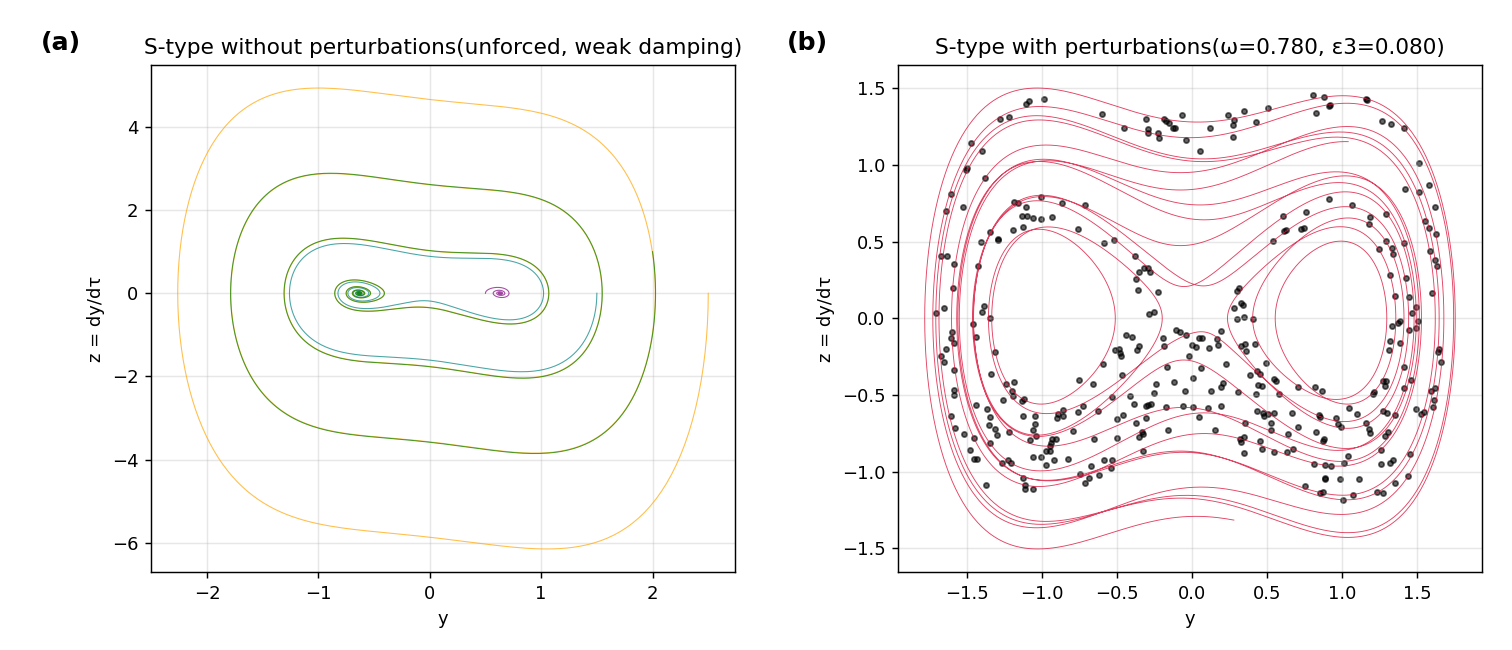
5. Analysis of S-type coronary vessels under small perturbations

5.1. S-type mathematical function

To capture additional physiological influence on arterial wall displacement, we extend the S-type subsystem to

$$ \begin{array}{c}\frac{{\mathrm{d}}^2\mathrm{y}}{\mathrm{d}{\mathrm{t}}^2}+\delta \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}-\alpha y+\beta {\mathrm{y}}^3=\eta \cos \left(\mathrm{\zeta }\mathrm{t}\right)+\frac{{\mathrm{ϵ}}_1}{{\left(\mathrm{y}+{\mathrm{\delta }}_1\right)}^{\mathrm{n}}}+{\mathrm{ϵ}}_2\tanh \left(\mathrm{k}\mathrm{y}\right){\left|\mathrm{y}\right|}^{\mathrm{\gamma }}+{\mathrm{ϵ}}_3\sin \left({\mathrm{\omega }}_1\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}\right)\end{array}$$(18)

And, with  $$ \mathrm{y}=\mathrm{y}\left(\mathrm{t}\right)$$  and  $$ \mathrm{z}=\frac{\mathrm{d}\mathrm{y}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}$$ , to the first-order form

$$$ \begin{array}{c}\{\begin{array}{c}\dot{\mathrm{y}}=z\\ \dot{\mathrm{z}}=-\delta z+\alpha y-\beta {\mathrm{y}}^3+\eta \cos \left(\mathrm{\zeta }\mathrm{t}\right)+\frac{{\mathrm{ϵ}}_1}{{\left(\mathrm{y}+{\mathrm{\delta }}_1\right)}^{\mathrm{n}}}+{\mathrm{ϵ}}_2\tanh \left(\mathrm{k}\mathrm{y}\right){\left|\mathrm{y}\right|}^{\mathrm{\gamma }}+{\mathrm{ϵ}}_3\sin \left({\mathrm{\omega }}_1\mathrm{z}\right)\end{array}\end{array}$$$(19)

Here  $$ \mathrm{\delta }>0$$  represents viscous damping, while  $$ \mathrm{\alpha }>0$$  is the linear elastic recoil of the wall and  $$ \mathrm{\beta }$$  governs cubic stiffening. The right-hand perturbations encode physiologically motivated beyond the baseline damped-Duffing structure. The term  $$ \mathrm{\eta }\cos \left(\mathrm{\zeta }\mathrm{t}\right)$$  idealizes periodic pulsatile forcing from the cardiac cycle. The singular contribution  $$ \frac{{\mathrm{ϵ}}_1}{{\left(\mathrm{y}+{\mathrm{\delta }}_1\right)}^{\mathrm{n}}}$$ (with a small offset  $$ {\mathrm{\delta }}_1>0$$  preventing blow-up at  $$ {\mathrm{y}=-\mathrm{\delta }}_1$$ ) mimics rapid increases in restoring pressure as the lumen approaches a geometric or mechanical constraint, modeling near-occlusive narrowing or wall contact events, the exponent  $$ \mathrm{n}$$  controls the steepness of this barrier. The saturating nonlinearity  $$ {\mathrm{ϵ}}_2\tanh \left(\mathrm{k}\mathrm{y}\right){\left|\mathrm{y}\right|}^{\mathrm{\gamma }}$$  introduces asymmetric, amplitude-dependent modulation of wall compliance: for small  $$ \mathrm{y}$$  it is approximately polynomial, whereas for large excursions it plateaus, reflecting material saturation or recruitment limits in the vascular tissue;  $$ \mathrm{k}$$  sets the transition scale and  $$ \mathrm{\gamma }$$  shapes the growth rate. Finally, the velocity-dependent modulation  $$ {\mathrm{ϵ}}_3\sin \left({\mathrm{\omega }}_1\mathrm{z}\right)$$  couples oscillatory hemodynamic effects to the wall motion through the displacement rate. Together these perturbations enrich the S-type dynamics, enabling bursting responses, intermittent transitions between small and large amplitude oscillations, and routes to complex or chaotic behavior when the competing nonlinearities and time-dependent forcings interact.

5.2. S-type melnikov function

We express the Melnikov function of the S-type system as:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{s}}\left({\mathrm{t}}_0\right)={\mathrm{M}}_{\mathrm{S}}^0+{\mathrm{\epsilon }}_3{\mathrm{R}}_{\mathrm{S}}\cos \left(\mathrm{\omega }{\mathrm{t}}_0+\mathrm{\varphi }\right)\end{array}$$$(20)

With:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{S}}^0={\mathrm{M}}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}}+{\mathrm{M}}_{\mathrm{d}\mathrm{a}\mathrm{m}\mathrm{p}}+{\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}\end{array}$$$(21)

Where:

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}}^{\mathrm{S}}={\mathrm{ϵ}}_1{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(-{\mathrm{a}}_1{\mathrm{\mu }}_0+{\mathrm{a}}_2{\mathrm{\mu }}_0^3\right)\bullet \frac{1}{{\left({\mathrm{v}}_0+\mathrm{\delta }\right)}^{\mathrm{n}}}\mathrm{d}\mathrm{\tau }\end{array}$$$(22)

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{d}\mathrm{a}\mathrm{m}\mathrm{p}}^{\mathrm{S}}=-{\mathrm{c}}_1{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\dot{{\mathrm{\mu }}_0}}^2\mathrm{d}\mathrm{\tau }\end{array}$$$(23)

$$$ \begin{array}{c}{\mathrm{M}}_{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{\mathrm{S}}=-{\mathrm{ϵ}}_2{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\dot{{\mathrm{\mu }}_0}}^2\bullet \left(\mathrm{k}{\mathrm{sech}\left(\mathrm{k}{\mathrm{v}}_0\right)}^2{\left|{\mathrm{v}}_0\right|}^{\mathrm{\gamma }}+\tanh \left(\mathrm{k}{\mathrm{v}}_0\right)\bullet \mathrm{\gamma }{\left|{\mathrm{v}}_0\right|}^{\mathrm{\gamma }-1}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathrm{v}}_0\right)\right)\mathrm{d}\mathrm{\tau }\end{array}$$$(24)

The periodic part is:

$$$ \begin{array}{c}{\mathrm{C}}_1^{\mathrm{S}}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(-{\mathrm{a}}_1{\mathrm{\mu }}_0+{\mathrm{a}}_2{\mathrm{\mu }}_0^3\right)\bullet \sin \left(\mathrm{\omega }{\mathrm{\mu }}_0\right)\cos \left(\mathrm{\omega }\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }\end{array}$$$(25)

$$$ \begin{array}{c}{\mathrm{C}}_2^{\mathrm{S}}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(-{\mathrm{a}}_1{\mathrm{\mu }}_0+{\mathrm{a}}_2{\mathrm{\mu }}_0^3\right)\bullet \sin \left(\mathrm{\omega }{\mathrm{\mu }}_0\right)\sin \left(\mathrm{\omega }\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }\end{array}$$$(26)

$$$ \begin{array}{c}{\mathrm{R}}_{\mathrm{S}}=\sqrt{{\left({\mathrm{C}}_1^{\mathrm{S}}\right)}^2+{{(\mathrm{C}}_2^{\mathrm{S}})}^2}, \varphi \ne \arctan \left(\frac{{\mathrm{C}}_2^{\mathrm{S}}}{{\mathrm{C}}_1^{\mathrm{S}}}\right)\end{array}$$$(27)

5.3. S-type criterion

The sufficient condition for the existence of homoclinic chaos is:

$$$ \begin{array}{c}\left|{\mathrm{M}}_{\mathrm{S}}^0\left({\mathrm{ϵ}}_1,{\mathrm{ϵ}}_2\right)\right|<{\mathrm{ϵ}}_3{\mathrm{R}}_{\mathrm{S}}\end{array}$$$(26)

This criterion reflects the balance between damping/singular effects and periodic excitation. If it is satisfied, then the stable and unstable manifolds of the homoclinic orbit intersect transversally, implying chaotic dynamics in the S-type system.

6. Conclusion

A nonlinear dynamical framework has been developed to represent coronary arterial wall motion, embedding distinct N-type and S-type responses within a common two-state coupled system. The framework incorporates linear and nonlinear wall recoil, flow-mediated feedback, a derivative coupling pathway, periodic cardiac-like forcing, and optional singular and saturating terms. The Melnikov method is applied to the reduced equations, revealing conditions for homoclinic/heteroclinic manifold splitting under periodic excitation. The model family reduces to analytically tractable Duffing-type forms with clear biomechanical interpretability. Computational experiments show that trajectories decay regularly into single or double-well equilibria, defining distinct basins of attraction in both N-type and S-type regimes. The framework establishes a transparent analytical and computational bridge between vascular biomechanics and nonlinear dynamics, highlighting the utility of chaos-based diagnostics for identifying and characterizing maladaptive coronary wall motions.