1. Introduction

In today's world, with the rapid development of science and technology, new terms such as artificial intelligence, 5G mobile communication, and virtual reality have been integrated into the public chat. As for the unfamiliar term "quantum", the application of it in communication and computing has become increasingly abundant. With the successful construction of China's "Mozi" quantum satellite and ground quantum communication network in the past two years, quantum mechanics has been deeply rooted in the hearts of people through various publicity reports such as TV, the Internet, and newspapers. It is believed that in the near future, quantum physics will bring subversive scientific and technological revolution to the society and completely change the way people live and think. However, the public still does not know where "quantum" comes from and what it means very well even though many movies and TV series related to quantum are emerging in an endless stream. This paper will start from introducing the glory of classical physics in the late 19th century and its cracks, and then show the birth of quantum mechanics step by step, so that people can have a more comprehensive understanding of quantum mechanics.

2. The last glory of classical mechanics

In the 19th century, scientists believed that they had completed most of the work in understanding the world. Basically, they could use the classical theory to explain everything (force, light, thermal, and mechanism), but there were actually a great number of flaws in the classical theory.

2.1. Newton’s classical theory

Mechanics has been established as a mature science that can describe the motion in a clear way since the publication of Isaac Newton’s Philosophiae Naturalis Principia Mathematica in 1687. Pierre-Simon Laplace even made an assertion that human can use Newton’s equation to predict the future of the universe as long as they have unlimited computing power and know the position of all particles at the same time [1].

2.2. Maxwell theory of electromagnetism

In 1873, James Clark Maxwell gave the famous equations of electromagnetism and discovered that the velocity of electromagnetic waves was the velocity of light, which has been the greatest triumph in the 19th century. He as well as other scientists thought that these waves are oscillations in an all-pervading elastic medium, which was named as ether [1].

3. The cracks of classical mechanics

3.1. Michelson-Morley experiment

The Michelson-Morley experiment performed in 1887 was proved to be the test for disproving the ether hypothesis that had dominated physics in the 19th century. Michelson thought about this problem and planned the ether-drift experiment. He did the experiment with Morley in Cleveland. This famous experiment was designed to measure the motion of the earth through ether by comparing the velocity of light in two perpendicular directions. The experiment that carried out in 1887 gave a convincing result that ether did not exist [2]. It was regarded as one of the clouds in physics.

3.2. Black body radiation

In 1800, William HerSchel discovered that heat and light belonged to the same spectrum. In order to quantify the spectrum, it was necessary to measure the energy of radiation appearing at different wavelengths. So a detecting material was then needed to absorb the total radiation at all wavelengths.

Gustav Robert Kirchhoff, a German physicist, was interested in this problem. His studies in 1860 pointed out that when such a material is heated, it will emit radiations of all wavelengths which makes it a perfect emitter. Such a body is regarded as a black body, a material that appears black behaves.

In 1893, Wien discovered the relationship between the energy emitted per unit volume per sec and the wavelength of radiation.

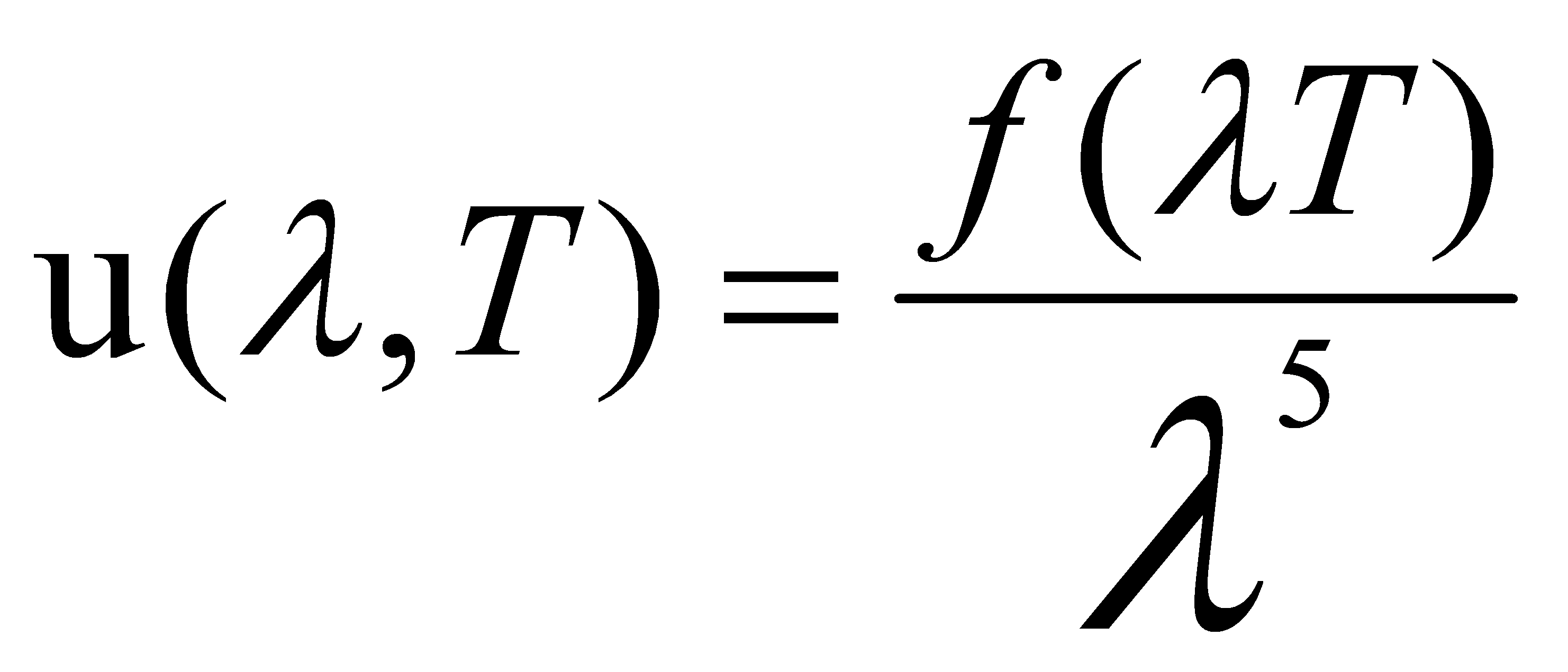(1)

Wien showed from this relationship that the highest energy value and the wavelength corresponded are all related to the temperature of the black body [3].

In 1900, Plank suggested that a harmonic oscillator can only have energy in integral multiples of a quantum of energy, where f is the frequency of the oscillator and h is a constant to be determined. It was the equation that made the quantization of the emitted energies of an oscillator, which was completely against the classical theory. That was when quantum mechanics was born.

4. Photoelectric effect and wave-particle duality

The photoelectric effect refers that under the irradiation of electromagnetic waves higher than threshold frequency, electrons inside some substances absorb energy and escape to form current.

4.1. Early Research

In 1902, Lenard found that in the photoelectric effect, the energy of the electrons depended on the wavelength of the light and the electrons were ejected immediately when the light hit. Classically, it took time to absorb energy and with stronger intensity, more electrons would get excited more easily. So basically, Leonard and other physicists thought that the energy had to be contained within the atoms themselves. All the light was triggering the release of the electrons. Since the structure of the atom was unknown at the period, the explanation was actually quite plausible [4].

4.2. Explanation by Einstein

Albert Einstein wondered how the light (a wave) could interact with an atom which exists at merely a point. He made an revolutionary statement: “the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which ... can only be produced and absorbed as complete units” [5].

The “energy quanta” is actually known as photons currently. Einstein predicted that each of the quanta had energy that was a multiple of the frequency (E=hf).

Einstein claimed that a quantum could be absorbed by an electron, thus giving all its energy. The electrons required a certain amount of energy φ, a property of the metal itself (threshold energy), to escape from the surface of the medal. The residual energy E was observed as the kinetic energy ½ mv2 of the electron. The energy of the electrons would be different, since some may came from below the surface, while those with the maximum energy came right from the surface. As a result, the relation was actually quite a simple equation E = hf - φ, where E is the maximum energy of the ejected electrons.

4.3. De Broglie's matter wave hypothesis

De Broglie assumed that microscopic particles have wave-particle duality, which clearly distinguishes them from macroscopic objects. There was no doubt that the motion of all macroscopic bodies is in accordance with Newton's equations and the laws of motion of classical mechanics. The development of the old quantum theory made people realize that the micro particle would not be able to obey Newton's laws and a new mechanics theory was needed to be established. As a result, De Broglie had made his own equation:

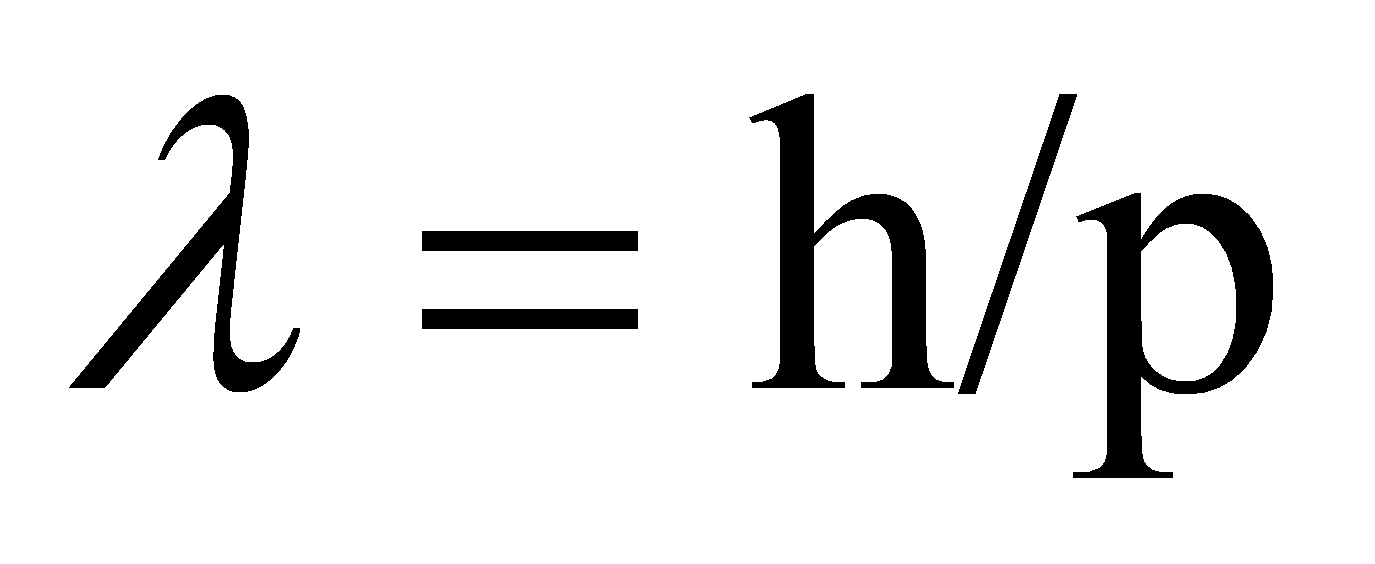(2)

He succeeded in finding the relationship between the wavelength of microscopic objects and their momentum.

5. Schrodinger’s equation

Inspired by an article of Einstein, Schrodinger had the idea of modeling the motion of electrons around the nucleus in the form of waves. In January 1926, Schrodinger put forward the world-beating quantum mechanical wave equation:

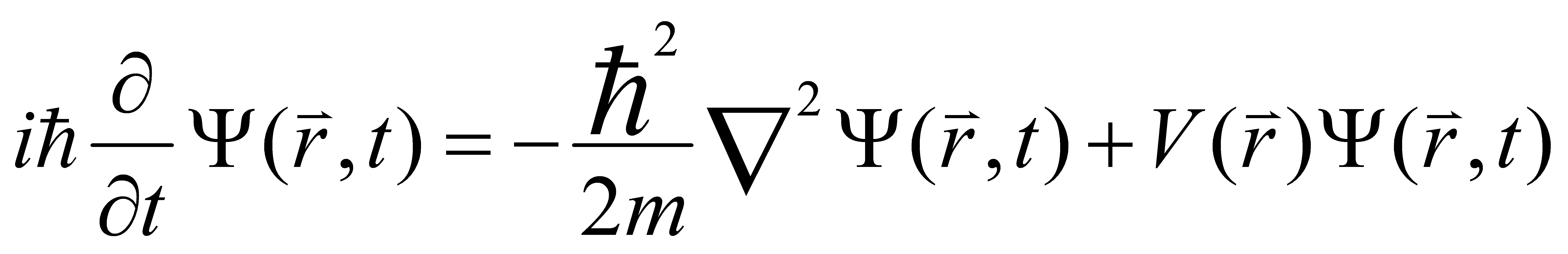(3)

Schrodinger did not restrict the problem to two dimensions as in ordinary mechanics. Since the wave-phenomenon is essentially three-dimensional, he used the wave function to express the status of microscopic particles [6].

Although, ironicly, this equation undoubtedly made quantum mechanics truly useful for studying various kinds of problems.

6. Quantum entangled state

Perhaps the most well-known quantum physics subject is Schrodinger's cat. In the early days of quantum mechanics, Einstein rejected this seemingly absurd entangled state. In 1935, with the support of the Einstein-Podolsky-Rosen (EPR) paradox (the wave function could not completely describe the physical reality), Schrodinger proposed an experiment that pushed the idea of EPR from micro to macro. In the experiment, cats were locked in a room with radioactive material. If the door was not opened, people would not know whether the cat is dead or not, so Schrodinger argued that the cats were in a state of being both dead and alive.

It was quiet strange, bcause according to the classical theory, the properties of a matter is independent, and whether the cat was dead or not did not count on the measurement.

6.1. Particle spin

In the classical physics, the particle processes angular momentum, which is the cross vector of position vector and the momentum. And the direction of the orbital momentum has no restrictions classically.

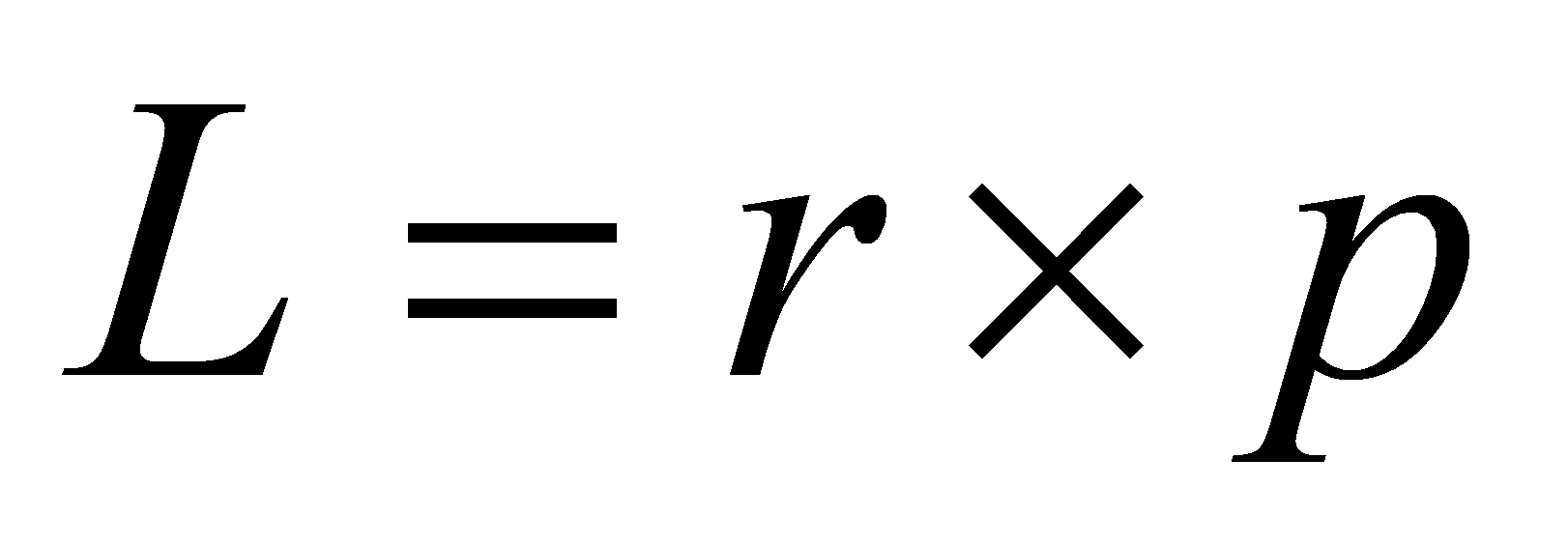(4)

When the particle carries a charge, it will move around itself and create a magnetic field. As a result, the particle will carry the magnetic momentum.

When it comes to the quantum mechanics part, things are different. The particles’ angular momentum only have the orientation between -l and l. The total spin of each particle and its components in any direction are determined by a non-negative integer or half-integer, called the spin quantum number, or 'spin' for short. That is the intrinsic property of this particle. The spin quantum number of electrons, protons, and neutrons is 1/2.

6.2. The Stern-Gerlach experiment

The experiment was firstly promoted in 1922 and illustrated that electrons process the angular momentum.

Heated silver atoms emerge from the oven, pass through an uneven magnetic field, and hit a screen that shows their positions.

The silver atom contains 47 electrons, 46 of which can be regarded as forming a spherically symmetric cloud with zero angular momentum. If the nuclear spin was ignored, the atom as a whole has an angular momentum that comes only from the spin momentum of the 47th electron. The result is that the silver atom as a whole can be seen as having only one magnetic moment (which corresponds to the spin of the 47th electron).

Silver atoms within the oven should have owned orientations that are completely random, according to the classical theory. Silver atomic beam’s magnetic moment of z component shall be any value. As a result, the beam through the magnetic field should be spun into a strip area. However, because orbital angular momentum is known to take on only odd values in quantum mechanics, the result of this experiment actually showed that the beam of silver atoms split into two, corresponding to the only two orientations of the magnetic moment which revealed an intrinsic duplicity (known as up/down) of the particles, the spin property [7].

Each atom has a 50-50 percentage to go up or down. So the position of the silver atoms cannot be told before the observation. It was the measurement that decides whether the atom goes up or down.

6.3. Principle of superposition of states

So, these atoms can be described as in an entangled state, and the scientists proposed a theory that quantum system has a different state of possible conditions,

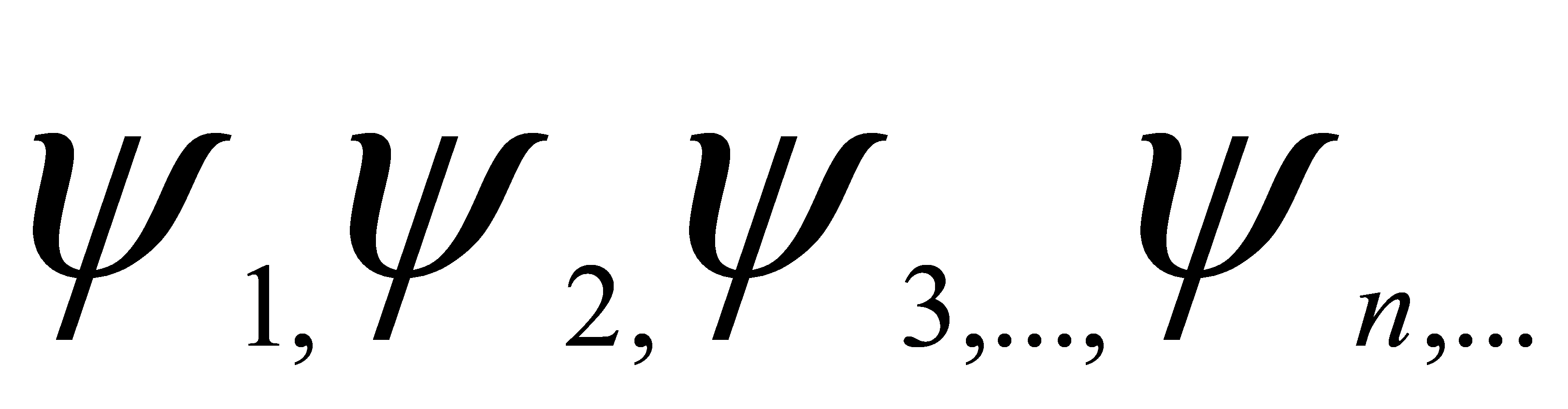
The linear combination is also a member of the system,

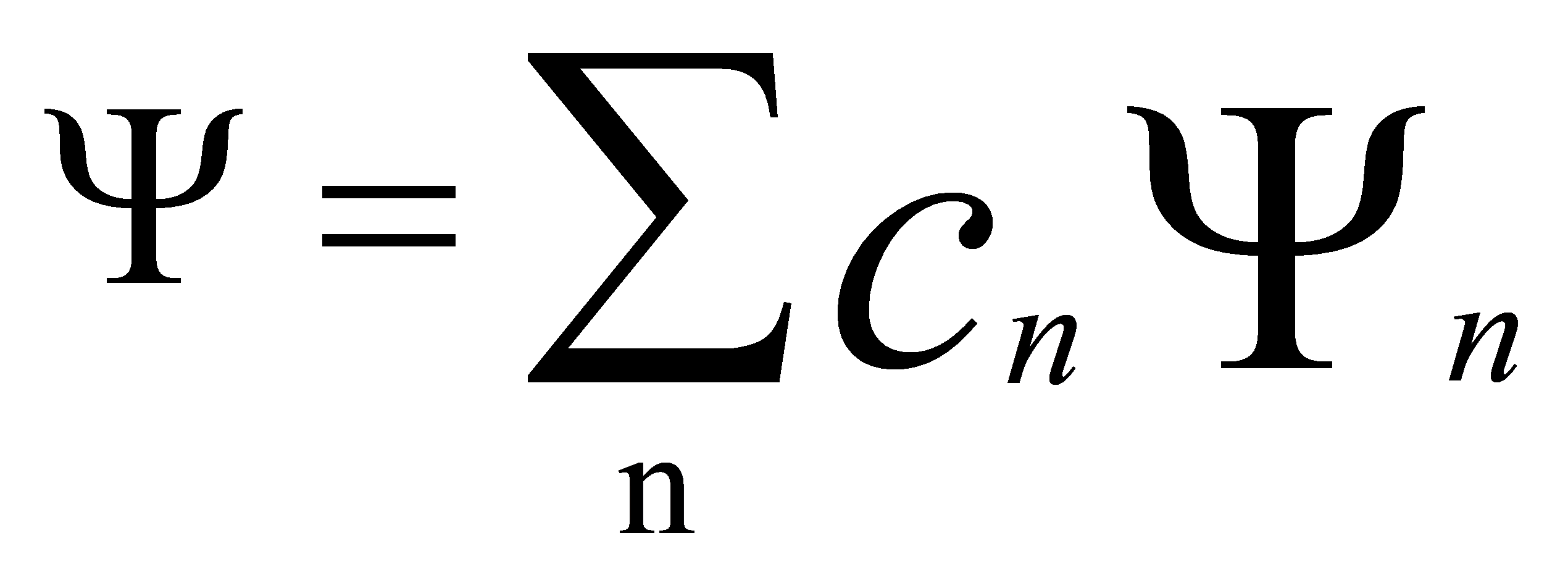(5)

where c1 and c2 are complex constants. This is the principle of superposition of states in quantum mechanics.

7. Copenhagen interpretation

In the 1920s, Bohr, Heisenberg and other scientists proposed a conception of nature radically different from that of their predecessors. According to the new view, the nature at the atomic level ought to be described by the probability functions and it is the measurement that decides the status of the microscopic particle. This concept, called the Copenhagen interpretation, was extremely challenging at the beginning, but after the 1930s, the interpretation nominally became accepted by almost all textbooks and scientists related to quantum mechanics [8].

7.1. Uncertainty principle

In 1927，Werner Karl Heisenberg came out with this theory.

The theory describes that:

(1) It is impossible to measure the microscopic particle’s position and momentum simultaneously.

(2) It is impossible to measure the position without disturbing momentum [9].

(3) , the product of the change of position vector and the change of momentum is larger than or equal to half of H cap (Plank constant divided by 2pai). The more certain the momentum of the microscopic is, the more uncertain its position vector will be.

(4) 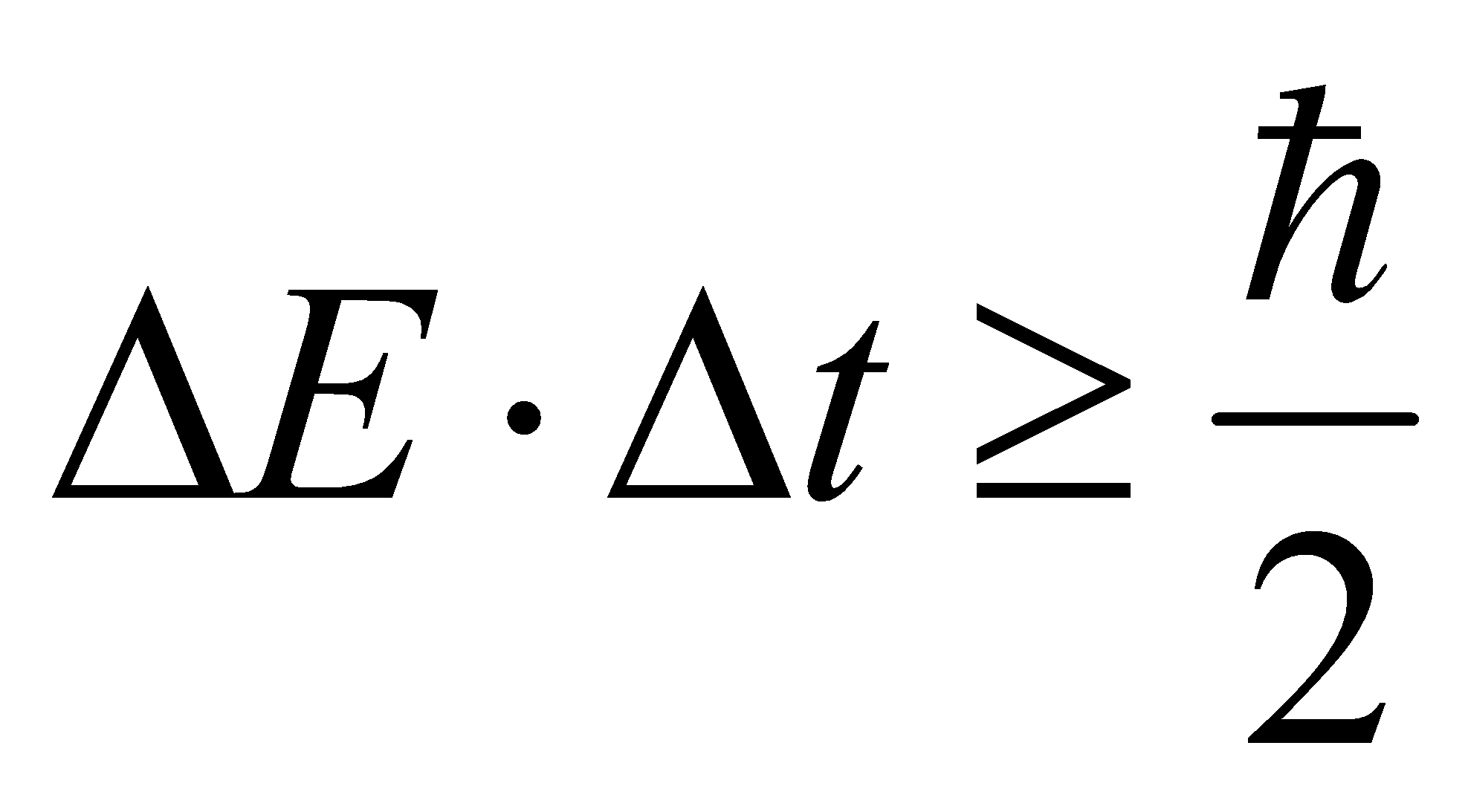, the product of the energy and the time particle stays at that energy level is larger than or equal to half of H cap. The longer an atom stays in a certain energy level, the smaller the energy width is, and the narrower the spectral lines it emits.

Classical physics believed that small particles and large cosmic bodies can be recognized through human measurement activities, thus knowing what will happen next second. And the uncertainty principle was undoubtedly the biggest challenge to this theory. If scientists cannot know the state of tiny particles, then predicting the macroscopic world made up by particles seems to be impossible.

7.2. Statistical interpretation

In the same year as Schrodinger came out with his equation, Born introduced probability to describe the status of particles. The ψ squared, exactly, is the probability that a microscopic particle is in some place. The particle itself does not spread out like a wave, but the probability of its occurrence is like a wave, strictly following the distribution of ψ square. The reason for the use of square was that the status of particles was described using complex numbers, which needed to be transferred into numbers in that way. In classical mechanics, the coordinates of the particles at a certain moment was an important property to describe the status of the particle’s motion. However, it seems that in quantum mechanics, the coordinates cannot describe the status of the microscopic particles exactly, on the other hand, probability should be used [10].

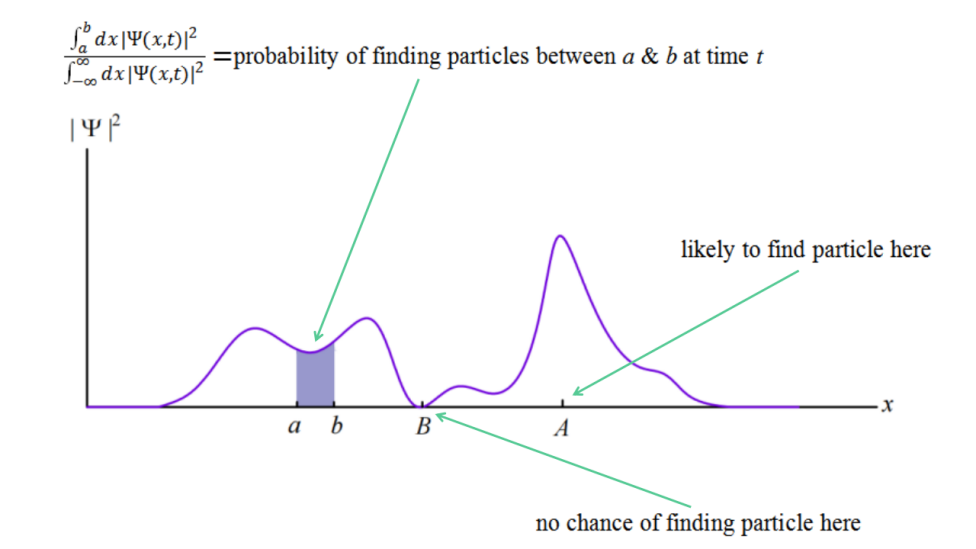
Figure 1. The probability of finding the particle in the interval from a to b achieved by integration.

8. Conclusion

This paper mainly illustrated the cracks that occurred in classical physics. Then the author introduces the birth of the quantum mechanics and some of the most important concepts in it. However, because of the author’s insufficient knowledge of mathematical, this paper does not demonstrate the specific derivation of the formula in quantum mechanics, but only clarifies its meaning. In the 21st century, the application of quantum mechanics in communication and computing is getting increasingly rich, and many technologies have been popularized and used. Quantum key distribution (QKD) is a method that uses quantum mechanics to provide unconditionally secure shared keys for both parties to ensure absolutely secure communication. The unconditional security of quantum key distribution benefits from a fundamental property of quantum mechanics: the quantum state cannot be replicated, so an eavesdropper cannot obtain valid information in it [11]. It is believed that in the near future, quantum physics will bring subversive scientific and technological revolution to the society and completely change the way people live and think.