1. Introduction

With the rapid development of science and technology, the scale of some infrastructure construction in urban life is becoming increasingly larger and larger. It is necessary to design and analyze some models to solve the problem of finding the shortest distance, which can solve problems like material loss and cutting expenses. The greedy algorithms will involve applications such as laying pipes, wires and optical cables between cities, finding shortest paths in communication networks, Internet of Things and transportation networks [1]. For the significance of the research, the minimum spanning tree is to strive for the least time and cost on the basis of the cost, such as laying architecture water pipes in the city. The greedy algorithm based on the minimum spanning tree can reduce the overhead and save the material cost. It can be modeled as vertices and the edges with weight between them. The purpose of designing and analyzing this MST is to find the minimum total distance so as to minimize the cost consumption, make it more convenient and save time and energy. This paper will devote into this problem and compare the methods to refine the most suitable condition respectively. Kruskal’s algorithm is nice of a mutually exclusive set data structure [2]. Predecessors will often take out the analysis, and there are many articles comparing the two algorithms in detail [3]. There are some papers that analyze whether there is a ring from the perspective of DFS(depth First Search) [4]. However, the main solution of this paper is through disjoint union set.

2. Comparative analysis of algorithms based on minimum spanning tree

Kruskal and Prim’s algorithm are two of the most classical greedy algorithms for generating minimum spanning trees of undirected connected graphs with weight.

2.1. Minimum spanning tree (MST)

A spanning tree with the lowest total edge weights is the shortest spanning tree of the original graph in an undirected connected graph with weights. The MST’s characteristic is: assume that U is a non-void proper subset of the vertex set V and that G=V, E> is a connected graph. There must be a minimal spanning tree of G that includes this edge if (u, v) is an edge of G, one of its linked vertices is in U(u∈U), and the other is not in U(v∈ v-u), also having the minimum weight (u, v).

The fundamental greedy solution to this problem is to construct an edge of the smallest spanning tree at each step. Set A is a variable that is tracked by the technique to guarantee that set A is always a subset of the minimal spanning tree prior for each iteration of the loop. The solution to this problem lies in locating the “safe edge,” which demands that if X is the least spanning tree of Y, then it must be confirmed that X∪{(u, v)} is still a subset of MST. Let’s use contradiction to explain this characteristic [5]. Let’s say that none of the minimal spanning trees of Y include (u, v). X doesn’t include (u, v). The edge has one end in U and one end in V-U because there must be an edge (u1, v1) in X linking the set of V-U vertices with the set of U vertices. X is not a spanning tree if there is no such edge between V-U and U.

2.2. Kruskal algorithm

Kruskal algorithm uses disjoint Union set to reduce time complexity and generate a minimum spanning tree. In this algorithm, each connected blocks will be seen as a set, Kruskal will sort the edges at the very beginning. Each vertex is an isolated and they belong to n independent sets. Then enumerate each edge in order. If this edge connects two different sets, then add this edge to the minimum spanning tree, so that these two different sets have merged into one set. If the two points connected by this edge belong to the same set, skip it until you have enumerated n minus 1 edges.

The most important part is that after adding the new edge, the key step is to judge whether it has formed a ring or not. It’s the core of the Kruskal algorithm [6].

The detailed steps are as follows:

Step a: The m edges should be sorted from the smallest to the largest according to the weight of the edges. \( { a_{1}}{,a_{2}} \) .. \( {a_{m}} \)

Step b: Add the sorted edges one by one to the MST set;

Step c: Judge whether there is a ring or not, that is G [S∪{ \( {a_{j}} \) }] does not contain rings [7]. We just need to check whether the two vertices of \( {a_{j}} \) contain the same branch in T. In other words, check whether the two vertices of \( { a_{j}} \) are connected in T, that is check the connectivity.

Step d: Merge the connection vertices;

For step c, disjoint union set is a good method. For each connection, find the ancestor of the two vertices to be connected until they find their first ancestor. Then compare, if they are the same, it is connected and can’t be connected any more, otherwise it can be connected. For each successful connection, those who are added to the “connected” set later will recognize the vertex that is already in the set as “father”. If both vertices are added to the set for the first time, then they are able to recognize ant vertex as “father”. For every successful connection between two families, the first ancestor of one family fathered the first ancestor of the other family. So, as long as the original ancestor is the same, it will absolutely form a ring.

Next is the pseudo-code to analyze its algorithmic complexity. Assume that the graph has n edges and m vertices.

1. A= \( ∅ \)

2. For vertex in G,V

3. Construct a set V

4. Sort by weight

5. construct a find-set

6. For each edge(u,v) \( ∈ \) G, add it to the MST

7. If find-set(u) \( ≠ \) find-set(v)

8. A=A \( ∪ \) {(u,v)}

9. merge (u,v)

10. return A

The time complexity in step 4 is O(nlogn), in step 7 is O(n+m) \( α(m) \) . Since each sub block is not nested but sequential, the one with the highest time complexity is O (nlogn).

3. Prim’s algorithm

The process of finding the minimum spanning tree by Prim’s algorithm adopts the idea of greedy algorithm. For the connected network containing n vertices, Prim’s algorithm finds an edge with the lowest weight from the connected network each time. This operation is repeated n-1 times, and the spanning tree consisting of n-1 edges with the lowest weight is the minimum spanning tree. Here we use a blue and white dot thought for better understanding the Prim’s algorithm. It is more graphic that the white dots represent vertices that are already connected using Prim’s, and the blue dots represent vertices that need to be connected. Each time a blue dot is whitened, the minimum of each blue dot to white dot group needs to be updated.

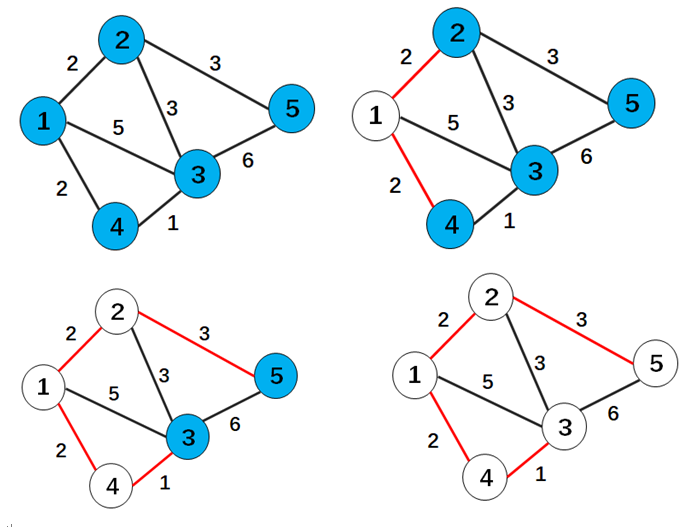
Figure 1. The procedure of determining the minimum spanning tree using the prim algorithm

As is shown in Figure 1, each vertex is marked in blue at the beginning. The first concern is to wash vertex 1, so we list the three edges that connected to vertex 1, and then we choose the shortest path2&4, next process is to find the shortest path that connected with 2&4. This will not end until all the blue dots are whitened.

Each time the Prim’s algorithm turns a blue dot U into a white dot, the minimum edge weight min[u] connected with the white dot is still the smallest among all the current blue dots. So add n-1 small edges to the spanning tree, and it ends up with a MST.

Here is a pseudo-code:

a) Initialization: min[v]= ∞(v≠1); min[1]=0; MST=0;

b) for (i = 1; i<= n; i++)

①Find the blue dot u with the smallest min[u].

②Mark u as a white dot

③MST+=min[u]

④For all the blue dots v connected to the white dot u

if (w[u][v]<min[v])

min[v]=w[u][v];

c) End of algorithm: MST is the sum of the weights of the minimum spanning tree;

The algorithm’s fundamental concept is: select the edge (u 0, v) that is connected to the starting vertex u 0 in the connected network G=V, E> and add its vertex to the vertex set U of the spanning tree [8]. The edge (u,v) with the lowest weight from each edge that has one vertex in U and the other vertex outside of U is chosen at each succeeding step, and its vertex is added to the set U. Continue doing this until the set U of spanning tree vertices contains all of the network’s vertices. The storage representation of the graph is the adjacency matrix.

The steps are:

1) Let the set of all vertices be V, and U be a subset of V, the set of edge is MST. At the beginning, the set of vertices U and the set of edges MST is empty;

2) Select a vertex from the set V of all vertices, set it as vertex No.1, add it to the vertex set U;

3) Of all edges associated with each vertex in U, first take an edge with the minimum weight ( \( {v_{i}},{v_{j}} \) ), where \( { v_{i}} \) ∈U, \( {v_{j}} \) ∈V-U;

4) Add edge ( \( {v_{i}} \) \( {,v_{j}} \) ) to MST and vertex \( {v_{j}} \) to U;

5) If U=n, the algorithm ends; otherwise, the execution will continue from step 3.

4. Comparison

Kruskal’s algorithm is an edge-dependent algorithm. The basic principle is to sort the number of edge sets, and then use a Disjoint Set Union to distinguish the points that enter and the points that do not enter. Traverse the number of edge sets in order from the smallest to the largest. If the two vertices’ edge are not in a set, output this edge, and merge these two points. Prim’s Algorithm finds the point from the current point that has the shortest path to your set and then pulls that point to your home set , prints an edge, and refreshes the path length to the other points.

According to the execution process of the Kruskal algorithm, all edges need to be sorted according to weight from the smallest to the largest. On the premise that no loop is formed, the edges with the smallest weight are added to the minimum spanning tree in turn. Therefore, the Kruskal algorithm can be used when the number of edges is small. Before finding the minimum spanning tree node, Kruskal algorithm adds the sorted weight edges to the minimum spanning tree in turn. When all the nodes are added to the minimum spanning tree, the minimum spanning tree of the connected graph is found [9]. When the number of edges is large, you can use the Prim algorithm because it adds one vertex at a time, making it suitable for large numbers of edges. Kruskal’s complexity is related to the number of edges, while Prim’s complexity is related to the number of vertices, which describes the sparsity of the graphs. As a consequence, Kruskal’s algorithm is better for sparse graphs, and Prim’s algorithm is better for dense graphs.

5. Conclusion

The goal of the two greedy algorithms is to locate the smallest spanning tree. In terms of approach, Kruskal needs to identify the minimal weight of the next edge after sorting the weights, whereas Prim’s algorithm frequently uses a direct search. Kruskal only needs to sort the weights once to find the minimum spanning tree, whereas the Prim algorithm needs to sort the adjacent edges several times. As a result, Kruskal is more efficient than Prim. In conclusion, Prim’s algorithm is superior for dense graphs whereas Kruskal’s technique is superior for sparse graphs. For this paper, for the analysis part of the Kruskal algorithm, except for the disjoint union set, the paper didn’t fully analyze the other method to determine whether the ring is formed, such as DFS(depth first search). In the future, it will be specifically analyzed why the disjoint union set is the optimal method.

Acknowledgment

At the beginning, I will show my deepest appreciation to my professor, who gave me the wonderful curriculum. My teaching assistant, who gave me patient instructions, also helps me a lot. Without their help, I couldn’t have completed my thesis.