1. Introduction

Image reconstruction is a fundamental problem in the area of computer vision and image processing. It aims to recover the cropped and lost part of the image under the situation of incomplete observation. This process plays a very significant role in various applications, including medical imaging, remote sensing mapping, video surveillance, image transmission, and image compression [1,2]. In real-world conditions, image degradation may be caused by various factors, such as sensor errors, noise pollution, or data loss during wireless network transmission [3]. A typical type of degeneration is the random loss of pixels. The pixels are lost completely in this case, and justifying what the lost pixels are depends on the rest of the observation data. Reconstructing this kind of image is very challenging because the size, region, and distribution of the lost area are totally random. Not only are the details needed to be recovered, but the consistency also needs to be maintained [4].

In the past ten years, deep learning has made numerous achievements in image reconstruction, including noise reduction, deblurring, super-resolution, and image restoration [5,6]. Among various neural network constructions, the U-Net was considered the most popular one in the field of image reconstruction. This was because of its encoder-decoder structure with skip connections [7]. Initially, U-Net was designed for biomedical image segmentation [8]. However, it is able to combine multi-scale contextual information with precise spatial positioning [9], so it also behaves well in recovering irregularly lost data. Skip connection is able to directly transfer high frame rate details abstracted from the encoder to the decoder, which helps with the details recovery.

Although U-Net has been widely used in structured image restoration problems, research on dealing with random loss in data (for instance, Bernoulli-dropped images) is relatively less [4]. In the Bernoulli-based degeneration model, every pixel in the original image has a probability p to remain constant and a probability (1-p) to be removed completely. This setting can model many problems in the real world, like random sensor failures in imaging equipment, packet loss in image transmission over unstable channels, and incomplete sampling in compressive sensing [3]. Restoring images under this condition required the model to utilize the limited observation effectively and generate reasonable content in those disappearing pixels.

In this research, the application of a deep learning network based on the U-Net in recovering Bernoulli-dropped images was explored. A dataset containing 800 high-resolution images was found, and they were synthetically degraded by applying Bernoulli masks with a fixed retention probability. The degraded images and their corresponding Bernoulli-dropped images are input as pairs to the U-Net model. The model is trained in a supervised learning manner to restore the original images. The model is optimized using a mean squared error (MSE) loss function, encouraging accurate pixel-wise reconstruction. These methods utilize the U-Net’s ability to combine multi-scale contextual information and handle local details, making it able to generate content that is structurally consistent and visually coherent under the situation of high loss rate.

The main contributions of this research are as follows. Formulating and reconstructing the Bernoulli-dropped images problem into a supervised learning manner and providing an implementation framework that is extendable to similar issues, adapting the U-Net architecture for this task and evaluating its reconstruction performance on a custom dataset with controlled levels of random pixel loss, and presenting both qualitative and quantitative results, including visual reconstructions and error metrics, to demonstrate the model’s effectiveness and limitations.

The remainder of this paper is organized as follows: the second part reviews the image restoration, sparse observation recovery, and also the research about reconstruction using U-Net; the third part introduces the methodology, including constructing a dataset, Bernoulli-dropped image generation, and network construction design; In the end, the fourth part is for conclusion and the future research direction.

2. Literature review

Image reconstruction refers to the process of restoring a high-quality original image from incomplete or degraded observations. It has a wide range of applications in many fields like medical imaging, remote sensing, video surveillance, and wireless image transmission [1,2]. The methods used can be classified into two main types: traditional techniques and methods based on deep learning.

2.1. Traditional method

The early method for reconstructing an image mainly depended on interpolation (such as bilinear interpolation and bicubic interpolation) and sparse representation methods based on the transform domain. These methods worked well in tackling regular lost or low-noise environments. However, in the conditions of high loss rate or complex texture, this often leads to blurring and artifacts [1]. The compressive sensing theory provides a new mathematical framework for image restoration under the condition of sparse sampling, but the accuracy of the assumption of signal sparsity limits its performance.

Besides, Maximum Likelihood Estimation (MLE) is one of the important statistical methods in traditional reconstruction. MLE estimates the most likely original image by assuming that the observed data follows a specific probability distribution (such as a Gaussian distribution or a Poisson distribution) and then finding the parameters that maximize the likelihood function of the observed data under this distribution assumption [3]. In the restoration of medical imaging and remote sensing data, MLE was usually used to reconstruct based on the noise model, in order to enhance the statistical consistency of the results. However, this method highly depends on the accuracy of the assumed noise distribution. When the actual noise distribution does not match the assumed or irregular distribution (such as a Bernoulli distribution), the performance of MLE may significantly deteriorate.

2.2. Image reconstruction based on deep learning

In recent years, Convolutional Neural Networks (CNNs) have made significant progress in tasks such as image denoising, super-resolution, and image inpainting [5,6]. The Generative Adversarial Network (GAN) enhances the authenticity of the reconstructed images by introducing adversarial loss, while the attention mechanism improves the model's ability to fuse global and local features [9]. For instance, the WaveFill model proposed by Yu et al. [5] processes high-frequency and low-frequency information separately, based on wavelet decomposition, which significantly improves the texture details of the repaired area. Wei and Wu [6] enhanced the global consistency and local detail restoration capabilities by combining the context discriminator with the U-Net.

2.3. U-Net and improvement

U-Net was initially proposed by Ronneberger for use in biomedical image segmentation. Its encoder-decoder structure and skip connection mechanism are widely used in image restoration, segmentation, and super-resolution tasks, because of its ability to extract multi-scale features under the condition of maintaining spatial resolution [7]. The improved versions that have emerged in recent years include the introduction of residual structures, attention modules, and bidirectional feature transfer mechanisms [7,9]. Xiang et al. [7] proposed BiO-Net, which enhances the efficiency of feature transfer through bidirectional recurrent connections and performs exceptionally well in medical image analysis and reconstruction.

2.4. Restoring randomly lost and bernoulli-dropped

In the cases of wireless image transmission, sensor networks, and compressive sensing, etc., the pixels lost tend to be irregular. The Bernoulli-dropped model assumes every pixel has a fixed probability of p to be lost and 1-p to be kept, which can effectively model these situations [3,4]. Aggarwal et al. [3] proposed a projection-based cascaded U-Net, which achieved excellent results in MRI sparse sampling reconstruction. However, its application in the restoration of random missing data in natural images is still relatively limited. This research aims to implement effective restoration of images with a high loss rate by combining the Bernoulli-dropped model and the U-Net structure.

3. Methodology

This study focuses on the natural image reconstruction task under the condition of Bernoulli-drop point degradation and has designed and implemented an end-to-end reconstruction network based on the U-Net.

3.1. Problem definition, dataset, and preprocessing

Given the original image  $$ \mathrm{x}\in \left[\mathrm{0,1}\right]\mathrm{H}\times \mathrm{W}\times \mathrm{C}$$  and the Bernoulli random mask M $$ \sim $$ Bernoulli (p), the observed image is (1):

$$ \mathrm{y}=\mathrm{M}⨀\mathrm{x}$$(1)

where  $$ ⨀$$  indicates element-wise multiplication. The objective of this study is to learn the mapping function $$ \mathrm{ }\mathrm{f}\mathrm{\theta }\left(\mathrm{y},\mathrm{M}\right)$$   $$ \approx $$  x to reconstruct the image under known conditions, given the original image and mask.

This paper uses the DIV2K dataset released by the NTIRE 2017 Single Image Super-Resolution Challenge as the source of the original clear images, which included 800 high-resolution natural images, covering various scenarios and textures. It is suitable as a training and evaluation benchmark for reconstructing models [9]. Every image was first resized to 512×512 and turned to grayscale to lower the computational cost and focus on restoration. Then, the Bernoulli-dropped image to every grayscale image was generated using the mask M∼Bernoulli (p) (in this paper, p is 0.3), and the observation was obtained, and those not observed were marked zero. The train set will be shuffled in the stage of training; pixel value was generalized by [0,1]. To ensure reproducibility, the random seed is fixed, and the data partitioning is kept consistent [9].

3.2. Network construction

In this paper, a symmetric encoder-decoder U-Net model is used, consistent with the common paradigms used in image repair/reconstruction tasks. The network was constructed by three layers of down-sampling encoder, a bottleneck layer, and three layers of up-sampling decoder. The features of the encoder and decoder are fused on the same scale through jump connections, allowing for the balance of global context and fine-grained spatial information.

3.2.1. Basic convolution block CBR

Each stage employs a sequence of two layers of convolution, activation, and normalization stacking (Conv3×3 + ReLU + BatchNorm), written as CBR (in_channels, out_channels). This is consistent with the CBR function in the code, which can maintain the stable growth of the receptive field while suppressing the internal covariate shift and improving the training stability.

3.2.2. Encoder (downsample), decoder (upsample) and bottleneck

The input is a single-channel grayscale image1×H×W. There are three layers:

1. enc1 = CBR (1→64), maintain resolution.

2. enc2 = CBR (64→128), followed by MaxPool2d (2) halves the resolution.

3. enc3 = CBR (128→256), the down-sampling is also achieved through the maximum pooling operation.

The maximum pooling gradually expands the receptive field layer by layer, enabling the bottleneck layer to gather more contextual information from a wider range.

middle = CBR (256→512), used to extract high-level semantic features at the minimum spatial resolution, serving as the global condition for the decoder's reconstruction.

At the decoding end, the resolution is restored through deconvolution upsampling, and it is concatenated with the encoded features of the symmetric layer:

1. up3: ConvTranspose2d (512→256) upsample and followed by e3, dec3 = CBR (512→256).

2. up2: ConvTranspose2d (256→128) upsample and followed by e3, dec2 = CBR (256→128).

3. up1: ConvTranspose2d (128→64) upsample and followed by e3, dec1 = CBR (128→64).

The jump connection provides high-resolution edge and texture features of the same scale as the input, significantly reducing the detail loss caused by multiple downsampling.

3.2.3. Output layer

Map the channel numbers back to a single channel through Conv2d (64→1, kernel_size=1), and obtain the reconstruction result x^∈ [0,1]1×H×W. Since the training loss uses MSE, the output does not necessarily require explicit activation. The reasoning and visualization stage will trim the results to the interval [0, 1].

3.2.4. Tensor dimension flow (taking 512×512 as an example)

1×512×512 → 64×512×512 → 128×256×256 → 256×128×128 → 512×64×64 →256×128×128 → 128×256×256 → 64×512×512 → 1×512×512

Here, “→” indicates the size changes resulting from convolution/pooling/upsampling and concatenation, ensuring that the output has the same resolution as the input.

3.2.5. Design trade-offs

1. Using ConvTranspose2d facilitates end-to-end learning of the upsampling weights; if checkerboard-like artifacts occur, they can be replaced with bilinear upsampling + convolution.

2. Three-layer downsampling and upsampling strike a balance between performance and memory usage; deeper layers can increase the receptive field but will also increase computational complexity and the risk of overfitting.

3. The combination of BatchNorm and ReLU has good compatibility with mini-batch training; if the batch size is very small, GroupNorm can be considered.

3.2.6. Loss function and optimization strategy

The loss function is the mean squared error (MSE) (2):

$$ \mathrm{L}=\frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{i}}^{^})}^2$$(2)

The optimizer is Adam, with an initial learning rate of  $$ 1\times {10}^{-3}$$ , a batch size of 4, and 10 epochs of training.

4. Result

The image reconstruction model based on U-Net proposed in this paper was evaluated on a dataset consisting of 800 grayscale images. As Figure 1 shows, the Bernoulli-dropped image (p=0.3) is input to the model to be reconstructed.

As shown in Figure 2, the damaged input image is processed by the trained model to generate a reconstruction result, which is then compared with the real image.

The result indicates that the model is able to reconstruct most of the information and texture under the condition of high density of dropped pixels.

To show the performance further, the MLE method is also used to construct an image in Figure 3.

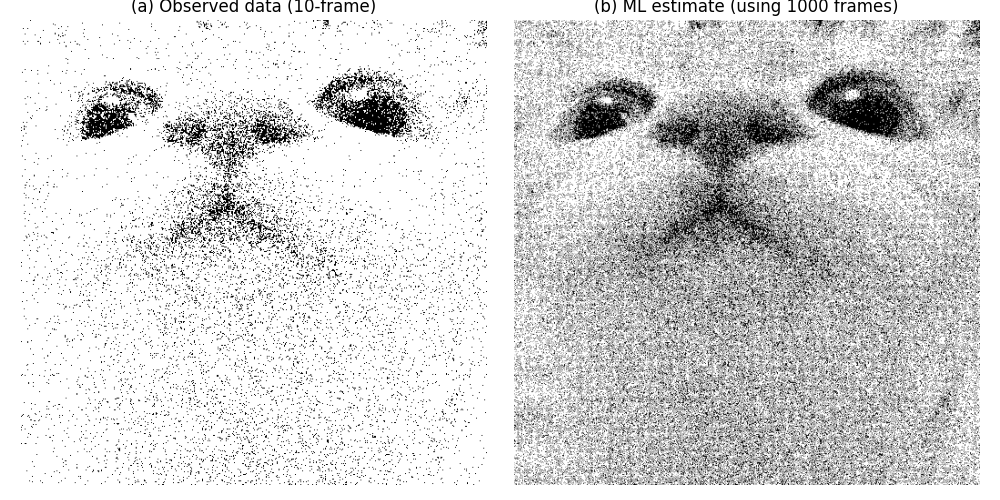
The MLE method uses 1000 frames of observed data for statistical reconstruction, while the U-Net model in this paper can complete the reconstruction with just a single damaged image. In the comparison, the method presented in this paper outperforms others in terms of the sharpness of edge restoration and the preservation of fine details in high-frequency textures. However, the MLE results often exhibit excessive smoothing in certain areas due to their reliance on statistical averaging.

The advantages of using the deep learning method over the traditional method:

1. Data-driven learning - The model can adapt to changes in data distribution and has greater robustness against noise, ambiguity, and random artifacts.

2. The inference speed is fast - after the model is trained, reconstructing a single image takes only milliseconds, making it suitable for real-time applications.

3. Higher reconstruction capability - The U-Net architecture is capable of capturing multi-scale features, thereby achieving more accurate restoration in structurally complex images.

Overall, the deep learning image reconstruction method proposed in this paper not only outperforms the classical methods in terms of visual quality but also has significant advantages in terms of efficiency and scalability. It provides an efficient and feasible solution for image restoration tasks in practical applications.

5. Discussion

This paper describes an experiment on reconstructing a Bernoulli-dropped image using the U-Net CNN. The results show that this method is significantly better than the one using MLE in terms of structural information recovery and detail restoration, especially in situations with a high pixel-dropped rate. The advantages mainly stem from the skip connection in the U-Net, enabling the model to preserve partial edge and texture characteristics effectively.

Although there is a limitation, first of all, in an extreme situation, such as having an extremely high pixel drop rate (p < 0.2), the problem of excessive smoothing or blurred texture will easily occur. This indicates that the model still has room to improve when handling extremely sparse observations. Secondly, in this experiment, only single-channel grayscale images were used for training and evaluation. In contrast, in actual situations, colorful images and more complex data distributions may require a higher ability from the model. Additionally, this paper only uses MSE as the loss function. MSE can ensure pixel-level restoration accuracy, but it is not good at sensing quality. In the future, it can be attempted to combine perceptual loss or structural similarity (SSIM) loss to further enhance the reconstruction effect.

Another notable aspect is the model's generalization ability. Although the experiments show that the U-Net performs stably on both the training set and the test set, its applicability when dealing with cross-domain data (such as switching between medical images and natural images) still needs further verification. This suggests that future research can introduce self-supervised or transfer learning methods to enhance the model's universality and robustness.

6. Conclusion

This paper proposes implementing the novel deep learning method based on the U-Net, aiming to reconstruct an image with randomly missing pixels. The research first constructed Bernoulli-dropped images using the DIV2K dataset. The experiment results show that this method outperforms the traditional maximum likelihood estimation method in terms of structure restoration, detail restoration, and reconstruction efficiency. To be more specific, the U-Net model remains capable of producing complete images despite high pixel loss rates and has an advantage in computational speed, making it suitable for real-time or large-scale image restoration scenarios.

The contributions of this paper are primarily in three parts: first, formalizing the Bernoulli-dropped image reconstruction problem as a deep learning task and providing a reproducible implementation framework. Secondly, the effectiveness of U-Net in the scenario of random data loss was verified, and it was compared with the classical methods. Lastly, this laid the foundation for subsequent research in color images, extreme missing rates, and cross-domain tasks.

The future work includes further optimizing the design of the loss function to enhance the perception quality; exploring deeper architectures or introducing an attention mechanism in the network structure to improve the performance; extending the method to color images and real transmission data; and combining self-supervised learning with generative adversarial networks (GAN) to enhance the robustness and generalization ability of the model.

Overall, this study not only demonstrates the potential of U-Net for reconstructing images with random pixel loss but also provides both practical and theoretical references for future researchers and scholars interested in similar subjects.