1. Introduction

Cancer is now the second leading cause of death in the world and will be responsible for nearly 10 million deaths in 2020 [1]. In the past, most cancer treatments relied on surgical resection, chemotherapy, and radiotherapy, which can cause serious side effects, but in recent years, immunotherapy has come into the picture for scientists. They started trying to utilize the human body's own immune system to treat cancer diseases. The main strategy is to exploit tumor-specific antibodies (passive immunotherapy) and the mechanism of cellular immunity (active immunotherapy) [2], aiming to decrease their suppression of the immune system. Currently, the three most popular categories are cytokines, vaccines, and monoclonal antibodies.

Although many new methods have been developed in humans’ ongoing battle with cancer, there are still many challenges. Biological systems are characterized by complexity and diversity, which makes it necessary to spend a lot of time and energy trying to find out the mechanisms or effects of drug treatments. However, by building mathematical models of tumor growth or pharmacokinetics, excessive experimentation can be prevented, and scientists can learn a lot of effective information for those diseases.

This paper is a comprehensive and brief review of the application of mathematical models in cancer immunotherapy research. It is divided into five sections. Section 2 deals with tumor-immune system interactions. Section 3 deals with the study of the effect of immunotherapy. Section 4 is about the search for the optimal situation. Section 5 is about the conclusion and discussion.

2. Mathematical models to describe tumor-immune interactions

Before introducing mathematical ideas and calculations into cancer treatment protocols, it is necessary for scientists to describe the mechanisms of tumor-immune interactions in mathematical terms.

Kuznetsov et al. proposed a mathematical model of the response of cytotoxic T-lymphocytes(CTLs) to tumor growth [3]. They defined ordinary differential equations (ODEs) for both immune effector cells and cancer cells. With this model, they predicted a tumor growth process with a 3- to 4- month deterioration cycle, which was validated to some extent by clinical research. Galach et al. considered the effect of time delay on the basis of this model to make it more complete [4].

De Boer et al. combined other cells and factors in immunodynamics to establish a model with a dozen differential equations to describe the anti-tumor immune response [5]. Also, they classified low- and high-antigenic tumors. Such a detailed model ultimately revealed the necessity of CTLs for the limitations of high antigenic tumors.

Those proposed mathematical models provide some theoretical foundations, mathematical equations, and important assumptions for later scientists to study the effects of cancer immunotherapy.

3. Mathematical models to study the effects of cancer immunotherapy

3.1. Cytokines and adoptive cellular immunotherapy

Cytokines are often used in conjunction with adoptive cellular immunotherapy (ACI). Cytokines are chemicals produced by immune cells. Among them, interleukin-2 (IL-2) is one of the few approved therapeutic drugs. Clinical studies have shown that they are able to activate the growth and expansion of immune cells, including cytotoxic T-lymphocytes (CTLs) and natural killer cells (NK cells) [6]. ACI refers to the injection of cultured immune cells into the host [7].

Kirschner and Panetta utilized mathematical models to establish the dynamic relationship between tumors, immune effector cells, and IL-2 [7]. In the model, E(t) refers to the concentration of immune effector cells, T represents tumor cells, and IL represents IL-2:

\( \frac{dE}{dt}=cT-{μ_{2}}E+\frac{{p_{1}}{EI_{L}}}{{g_{1}}+{I_{L}}}+{s_{1}}\ \ \ (1) \)

\( \frac{dT}{dt}={r_{2}}(T)T-\frac{aET}{{g_{2}}+T}\ \ \ (2) \)

\( \frac{{dI_{L}}}{dt}=\frac{{p_{2}}ET}{{g_{3}}+T}-{μ_{3}}{I_{L}}+{s_{2}} \ \ \ (3) \)

The first equation describes the rate of change in the concentration of the effector cell population , which is influenced by the antigenicity of the tumor, its own proliferation, and its external sources; The second equation uses a logistic growth model to describe the stimulation of the immune response to the tumor; The third one describes the production, depletion, and external sources of IL-2. Through the analysis, they predicted that it is difficult to achieve a good therapeutic effect by using IL-2 alone. If its input is low, it will not be able to destroy the tumor; If its concentration is high, it may have a pathological effect. However, it can achieve the effect of tumor elimination when treated concurrently with ACI.

Cappuccio et al. also used experimental results in mice as parameters to establish a model to study the relationship between IL-21 and tumors, but this model focused more on the effect of IL-21 on NK cells and CD8+ T cells [8]. The results showed that IL-21 can directly regulate the volume and function of these immune effector cells, and a therapeutic effect can be achieved for non-immunogenic tumors.

3.2. Vaccines

Dendritic cells (DCs) can be activated by tumor antigens in vitro. Therefore, the principle of DC vaccines is that DCs are able to be extracted from the body and then re-injected into the body carrying specific antigens [9].

Chaplain and Matzavinos developed a mathematical model to describe the growth of immunogenic tumors [10]. They developed a system of nonlinear partial differential equations for T lymphocytes, tumor cells, and their complexes. This model simulated the phenomena of dormancy and recurrence of cancer, and it was found that tumor-infiltrating cytotoxic lymphocytes play significant roles in the process. Joshi et al. made another model based on this one and added an antigen-presenting cell to it [11]. They investigated the role of antigen presentation and signaling pathways in tumor growth. It was shown that a cancer vaccine based on tumor antigen-pulsed DC cells was more effective in inhibiting tumor growth and recurrence than ACI, which provides some evidence for the active vaccination regimen.

3.3. Monoclonal antibodies

Studies have shown that the PD-1 receptor exists on T cells, and some tumor cells express programmed death ligand-1 (PD-L1). The combination of PD-1 and PD-L1 can inhibit T cell activity, thus suppressing the host immune system [12]. Therefore, in immunotherapy, scientists use anti-PD-L1 monoclonal antibodies to block immune checkpoints.

Radunskaya et al. developed a mathematical model to study combination therapy with monoclonal antibodies and DC vaccines [13]. In the model, the ability of one’s immune system is measured by a number of parameters representing the rate of tumor growth and the rate of T-cell killing. Then, they investigated the optimal way of combining and dosage of this drug by varying the dosage and schedule of the anti-PD-L1 drug. This type of modeling can be used for combination therapy studies and other immune checkpoint inhibitors, like CTLA-4.

3.4. Chemoimmunotherapy

Since it was found that some of the chemicals could kill rapidly dividing cells, they can be used to kill tumor cells, and this is called chemotherapy. Unfortunately, those chemicals will also kill some normal rapidly dividing cells, so the dose of drugs should be controlled strictly. Scientists recently combined the two therapies, and mathematical models help people analyze their feasibility and advantages.

De Pills et al. used ODEs to describe tumor growth in the presence of a combination of chemotherapy and cancer vaccines [14]. Through experiments and simulations in data of mice, they made some positive findings for chemoimmunotherapy. Later, they modified this model by incorporating baseline NK cell and activated CD8+ T cell concentrations from human data [15]. They found that chemoimmunotherapy was more useful in patients with higher immunocompetence. Based on this idea, Rodrigues et al. then established an ODE to verify the feasibility of chemoimmunotherapy for chronic lymphocytic leukemia [16].

For advantages, Pang et al. used numerical simulation to analyze the positive effect of the increase in the minimum effective concentration of the drug, and also verified that combination therapies lead to better therapeutic results [17]. Mamat and Subiyanto developed a mathematical model and applied it to two patients [18]. Ultimately, it came out that combination therapy is more effective than immunotherapy and chemotherapy alone.

4. Mathematical Models to Optimize Cancer Immunotherapy Regimens

In addition to classifying and predicting diseases and treatments’ effects, mathematical models have another important role in the biomedical field: calculating the optimal time and dosage of drug administration with the optimal control theory. When they build equations, they can select control parameters, such as the concentration of tumor cells or immune cells. Based on the numerical constraints on these parameters, they can acquire the optimal solution for the parameters by calculating the extreme values of the objective function [19].

Castiglione and Piccoli constructed a mathematical model to study the effects of DC vaccines [20]. They transformed it into a control problem by taking the mass of the tumor at the end of the treatment and the dose of the vaccine as a cost function. By using the hybrid control method, they calculated the interaction between the cost function and the time (Figure 1).

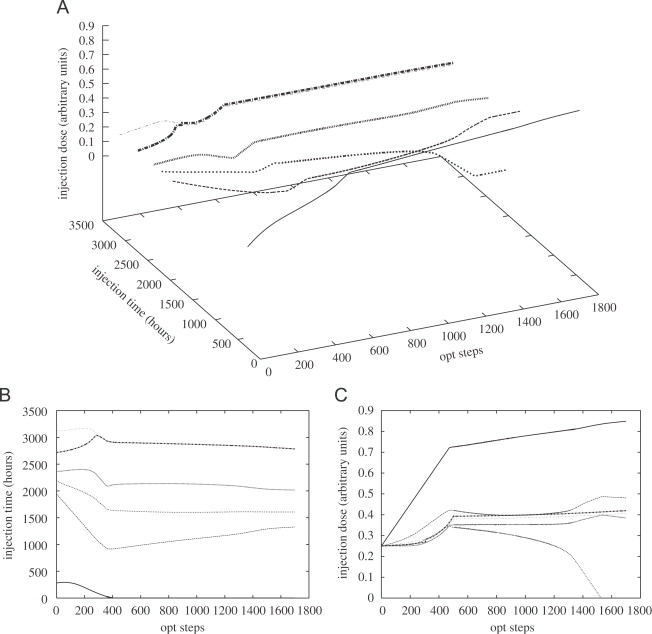
Figure 1. Evolution of the schedule during the optimization. A: the time and dose variation of cancer vaccination; B: the time variation of cancer vaccination; C: the dose variation of cancer vaccination

Figure 1A shows the time and dose variation of cancer vaccination. Figure 1B shows the time variation and Figure 1C shows the dose variation. It can be seen that a high dose of vaccination should be given at the beginning of the treatment, while a small dose of vaccine should be used several times later.

Qomlaqi et al. proposed a comprehensive mathematical model to describe the interaction between cancer and the immune system in mice [21]. They considered the roles of NK cells, cytotoxic T cells, helper T cells, regulatory T cells, DC, and IL-2. In the optimal plan of the simulation, they found that the DC vaccine ought to act before the maximum number of CD8+ cells.

5. Conclusion

In this review, the application of mathematical models to cancer immunotherapy is discussed. Many scientists first build models to describe the tumor-immune interaction by introducing some parameters about the growth rate of cells. Based on those models, scientists add some components to introduce the function of immunotherapy drugs. Therefore, they can develop a mathematical model to predict the effects of those drugs. While others often continue to modify and improve some useful models, they become closer to reality. Currently, scientists focus more on cytokines, cancer vaccines, and monoclonal antibodies, and the research method of modeling has made some contributions in all those different ways. Also, some scientists try to combine immunotherapy with traditional cancer treatment methods. Chemoimmunotherapy is one of the most popular, and many models have preliminarily verified its feasibility. In addition to predicting what will happen after the drug, mathematical models can also calculate when and how much the drug should be administered, which is accomplished through the use of optimal control theory. In conclusion, mathematical modeling has become a powerful tool in the field of cancer treatment research. It can provide some theoretical basis for efficacy and mechanism and can be used as a simulation experiment before clinical trials. However, there are still some problems. When scientists build their models, most of them will choose to simplify the situation, which can lead to some inaccuracies in the predicted results and can be fatal in the field of medicine. Also, much of the research remains theoretical, making it difficult to go further toward real-world applications. It may require the cooperation of mathematicians, biologists, and clinicians to realize In the future, scientists can further study the optimal solution of the combination treatment plan through mathematical modeling since it can avoid some of the side effects of traditional treatments. In the era of big data, mathematical models can also contribute to the field of precision medicine. By considering individual differences and data, the use of mathematical models to calculate the optimal dose for an individual and develop a personalized treatment plan may become the direction of future research.