1. Introduction

In the context of energy shortages and environmental protection, the improvement of energy utilization efficiency has become an important topic on a global scale [1-3]. As the core technology of energy conversion, the heat engine plays an important role in realizing sustainable energy utilization and directly affects energy utilization efficiency and environmental sustainability. However, in practical applications, the efficiency of heat engines cannot be greatly improved, which is often restricted by various factors [3-5].

In order to further improve the efficiency of the heat engine, this paper will explore ways to improve the application technology of the mainstream heat engine model in the real world to achieve more efficient energy conversion. First, a basic overview of heat engines and heat engine efficiency is introduced, and then the key concept of heat engine efficiency is discussed in depth. At the same time, in order to explain the efficiency of heat engines more specifically and clearly, this paper will choose two mainstream heat engine models, the Carnot heat engine and the Stirling heat engine, as examples and deeply discuss their working principles, theoretical derivations, influencing variables, and limiting factors in practical application. This study provides a systematic evaluation of the technical progress of heat engine efficiency technology, and has important reference value for promoting the sustainable and healthy development of technology in this field.

2. Overview of heat engines and its efficiency

2.1. Heat engine

A heat engine is a mechanical device that periodically converts the chemical energy of a fuel into internal energy and then into mechanical energy, such as steam engines, steam turbines, gas turbines, internal combustion engines, and jet engines. Heat engines usually use gas as the working medium, and use gas to expand by heat to do work. Theoretically, all heat engines should satisfy the following three conditions; the system absorbs heat from a high-temperature heat source, the system releases heat to a low-temperature heat source, and the network is periodically performed externally.

2.2. Efficiency of heat engine

Studies show that the heat engine cannot convert all the heat absorbed from the high-temperature heat source into work. That is, the efficiency of the heat engine cannot reach 100% [2]. Any heat between the two temperatures of the engine does not produce entropy, because the entropy lost by the heat reservoir is exactly equal to the entropy gained by the cold reservoir, and the entropy of the system does not change as the system experiences a cycle. Therefore, the maximum efficiency of any heat engine must be less than the Carnot efficiency. In general, the entropy of the system increases as heat flows from a high to a low heat source. According to the current situation, it is necessary to increase the ratio of the heat converted into useful work to the total heat absorbed by the heat engine from the high-temperature heat source as far as possible through various technical means.

\( η \) is used to represent the efficiency of the heat engine, \( {Q_{H}} \) and \( {Q_{C}} \) respectively represent the heat emitted by the high temperature heat source and the heat absorbed by the low temperature heat source, and \( W \) represents the useful work done by the heat engine [6]. Then we can get:

\( η=|\frac{W}{{Q_{H}}}|\ \ \ (1) \)

Since the state of the system remains the same throughout the cycle, so the internal energy \( ΔU=0 \) . According to the first law of thermodynamics:

\( ΔU=Q+W\ \ \ (2) \)

Where: \( Q \) is the heat absorbed or released, when \( Q \gt 0 \) is endothermic heat, when \( Q \lt 0 \) is exothermic heat, \( Q={Q_{H}}-{Q_{C}} \) , \( W \) is the work done externally by the system.

Then we can get:

\( -W={Q_{H}}-{Q_{C}}\ \ \ (3) \)

Combining formula (1) and (3), the formula of heat engine efficiency can be obtained as follows:

\( η=\frac{{Q_{H}}-{Q_{C}}}{{Q_{H}}}=1-\frac{{Q_{C}}}{{Q_{H}}}\ \ \ (4) \)

3. Mainstream heat engine model and principle

3.1. Carnot heat engine

The Carnot heat engine is an ideal Icano cycle heat engine whose basic structure was proposed by French scientist Carnot in 1824. He envisioned a special cycle consisting of two reversible isothermal processes and two reversible adiabatic processes, called the Carnot cycle.

3.1.1. Carnot heat engine efficiency. As shown in Figure 1, the Carnot positive loop sequence is 1→2→3→4→1. Suppose the cycle contains Vmol of ideal gas. The state parameters at 1, 2, 3, and 4 are respectively \( ({P_{1}},{V_{1}},{T_{1}}),({P_{2}},{V_{2}},{T_{1}}) \) , \( ({P_{3}},{V_{3}},{T_{2}}),({P_{4}}, {V_{4}},{T_{2}}) \) . Where \( P \) and \( V \) are pressure and volume, respectively, \( {T_{1}} \) is the temperature of high temperature heat source, \( {T_{2}} \) is the temperature of low temperature heat source [1].

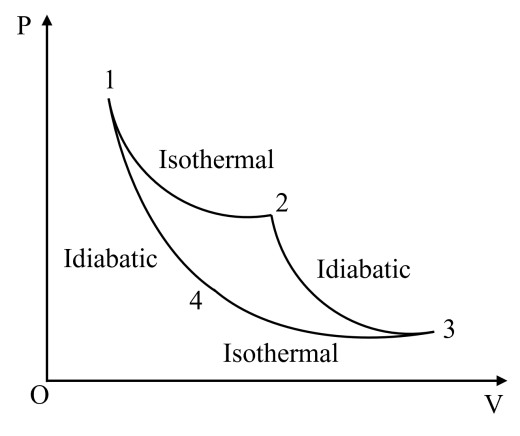
Figure 1. Carnot positive cycle.

As shown in Figure 1, in the adiabatic process 2→3, 4→1, there is no heat exchange during this process. Combined with formula (2), we can obtain:

\( -ΔU=PdV\ \ \ (5) \)

To raise the temperature of an object by one degree, the amount of heat required depends on environmental factors such as pressure and temperature, especially whether the outside world is doing work on it. The specific heat capacity of the object at this time is:

\( C=\frac{Q}{ΔT}=\frac{ΔU-W}{ΔT}\ \ \ (6) \)

Where \( ΔT \) is the temperature change.

Since the volume does not change during work done on the object, then \( W=PdV=0 \) . Then the specific heat capacity at the same volume is:

\( {C_{V}}={(\frac{∂U}{∂T})_{V}}\ \ \ (7) \)

It can be obtained by combining the ideal gas equation of state, \( PV=nRT \) :

\( -n{C_{V}}dT=(\frac{nRT}{V})dV\ \ \ (8) \)

Where n is the amount of the substance of the gas, and the unit is mol. \( R \) is the thermodynamic constant, \( R \) ≈8.314J/(mol·K).

Then combine \( γ=\frac{{C_{P}}}{{C_{V}}} \) , we can finally get:

\( {T_{1}}V_{2}^{γ-1}={T_{2}}V_{3}^{γ-1}\ \ \ (9) \)

\( {T_{1}}V_{1}^{γ-1}={T_{2}}V_{4}^{γ-1}\ \ \ (10) \)

Then analysis of the whole cycle step by step can be obtained:

Segment 1→2 is isothermal expansion, meanwhile \( {V_{2}} \gt {V_{1}} \) . The system does external work, the internal energy is unchanged, and the heat is absorbed from the high temperature heat source, so:

\( Δ{U_{1}}=0\ \ \ (11) \)

\( {W_{1}}=-\grave{Ο}_{{V_{1}}}^{{V_{2}}}PdV=-nR{T_{1}}ln{\frac{{V_{2}}}{{V_{1}}}}\ \ \ (12) \)

According to the first law of thermodynamics:

\( {Q_{1}}=Δ{U_{1}}-{W_{1}}=nR{T_{1}}ln{\frac{{V_{2}}}{{V_{1}}}}\ \ \ (13) \)

(ii) Segment 2→3 is idiabatic expansion, meanwhile \( {{V_{3}} \gt V_{2}} \) The system does external work, the internal energy is reduced, neither heat absorption nor heat release, so:

\( {Q_{2}}=0\ \ \ (14) \)

(iii) Segment 3→4 is isothermal compression, meanwhile \( {{V_{3}} \gt V_{4}} \) . The external environment does work on the system, the internal energy is unchanged, and the external heat is released, so:

\( Δ{U_{3}}=0\ \ \ (15) \)

\( {W_{3}}=-\grave{Ο}_{{V_{3}}}^{{V_{4}}}PdV=-nR{T_{2}}ln\frac{{V_{4}}}{{V_{3}}}\ \ \ (16) \)

According to the first law of thermodynamics:

\( {Q_{3}}=-{W_{3}}+Δ{U_{3}}=nR{T_{2}}ln{\frac{{V_{4}}}{{V_{3}}}}\ \ \ (17) \)

(iv) Segment 4→1 is adiabatic compression, meanwhile \( {{V_{3}} \gt V_{4}} \) The external environment does work on the system, neither absorbing heat nor releasing heat, so:

\( {Q_{4}}=0\ \ \ (18) \)

In summary, the efficiency of the Carnot heat engine is:

\( η=\frac{|{Q_{1}}|-|{Q_{3}}|}{|{Q_{1}}|}=\frac{nR{T_{1}}ln{\frac{{V_{2}}}{{V_{1}}}}-nR{T_{2}}ln{\frac{{V_{3}}}{{V_{4}}}}}{nR{T_{1}}ln{\frac{{V_{2}}}{{V_{1}}}}}=\frac{{T_{1}}-{T_{2}}}{{T_{1}}}=1-\frac{{T_{2}}}{{T_{1}}}\ \ \ (19) \)

The efficiency of Carnot heat engine is only determined by the temperature of high temperature heat source and low temperature heat source, so theoretically, the only way to improve the efficiency of Carnot heat engine is to increase the temperature of high temperature heat source and reduce the temperature of low temperature heat source.

3.2. Stirling engine

Stirling heat engine is an external gas turbine that can absorb heat from external sources for periodic reciprocating motion, and its cycle process is shown in Figure 2 [7]. The working substance can be air or any other gas, and the engine consists of two cylinders with pistons [5].

Although the shape of the ideal cycle of Stirling heat engine is similar to the three ideal cycles of the internal combustion engine, it is simpler than the ideal cycle of the internal combustion engine, which also shows that the factors affecting the efficiency of the Stirling heat engine are less than the ideal cycle of the internal combustion engine, and the way to improve the efficiency of the Stirling heat engine is simpler. And the whole process of Stirling cycle will not produce waste gas, so it will not cause pollution to the environment, meet the current requirements of energy conservation and emission reduction, but also reduce the heat taken away by the waste gas, improving the efficiency of the heat engine.

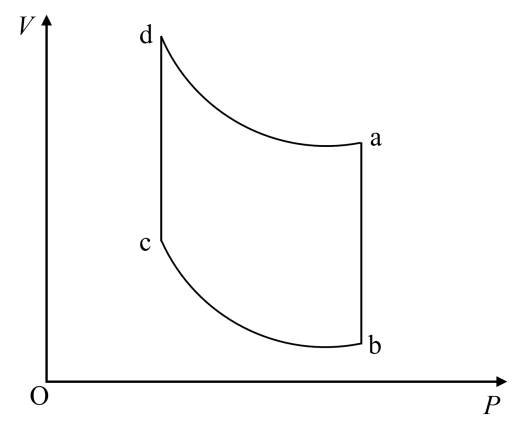
Figure 2. Stirling cycle.

As shown in Figure 2, the temperature in segment b-c is \( {T_{1}} \) . The system is an ideal gas, and its internal energy remains constant during the isothermal process, \( ΔU=0 \) . So, the heat absorbed is:

\( {Q_{1}}=-W=-\grave{Ο}_{{V_{A}}}^{{V_{B}}}(-PdV)={nRT_{1}}ln{\frac{{V_{c}}}{{V_{b}}}} \ \ \ (20) \)

The temperature in the d-a segment is \( {T_{2}} \) _, Similarly, the heat emitted can be:

\( {Q_{2}}={nRT_{2}}ln{\frac{{V_{a}}}{{V_{d}}}}\ \ \ (21) \)

Throughout the cycle: \( {V_{a}}={V_{b}} \) , and \( {V_{d}}={V_{c}} \) _. Therefore, the efficiency of this cycle is:

\( η=1-\frac{{T_{2}}}{{T_{1}}}\ \ \ (22) \)

In summary, the theoretical efficiency has nothing to do with other factors such as the nature of the working medium, and only depends on the temperature of the two heat sources.

3.3. Comparative analysis of heat engine

Carnot heat engine and Stirling heat engine, as two kinds of thermal energy conversion equipment, are similar in working principle, structure and performance.

The Carnot cycle is an ideal cycle consisting of two reversible isothermal processes and two reversible adiabatic processes. Its working principle is based on adiabatic expansion and compression, through the exchange of heat between the input heat source and the output cold source to complete a cycle. The Stirling heat engine is a cycle consisting of two isothermal processes and two isovolumetric processes. Its working principle is based on the periodic expansion and compression of gases and the exchange of heat between gases [6].

The Carnot heat engine is usually composed of a working medium and two constant temperature heat sources, of which the working medium can be any substance with ideal gas properties, while the Stirling heat engine is usually composed of a working medium, two heat exchangers, and two pistons.

The Carnot heat engine is theoretically the most efficient heat engine, and its efficiency depends on the temperature difference between the working medium and the low heat source. The efficiency of Stirling heat engine is relatively low, depending on the design of the heat exchanger and the characteristics of the working medium.

Therefore, the Carnot heat engine is often used in thermodynamics teaching and analysis, and is rarely used in practical engineering, while the Stirling heat engine is widely used in some specific fields, such as submarines, solar power generation, cold surface portable equipment, etc. [3]. However, from the theoretical model level, although the cycle process is different, the efficiency of the two heat engines depends on the difference between the high temperature heat source and the low temperature heat source.

4. Energy reduction application of heat engine model

Heat pump technology is an efficient heat transfer equipment based on the Stirling heat engine model. Its basic working principle is to input a small amount of high-quality power to achieve the transfer of low temperature heat to high temperature heat, generating the required convection and heat dissipation. Currently, commonly used heat pump types are electric driven steam compression heat pumps, absorption heat pumps, thermoelectric heat pumps, and so on. Heat pump technology has great application prospects and market potential in the fields of building heating and domestic hot water. Taking air source heat pumps as an example, the following three optimization suggestions can improve the efficiency of air source heat pumps:

• Design multi-mode flow control [8]. The research shows that the ambient temperature has a significant effect on the performance coefficient of the air source heat pump system, and the operating performance of the system is best when the ambient temperature is 30℃. If a single control mode is used, the performance coefficient of the air source heat pump system is not high most of the time due to environmental changes. Therefore, when designing the air source heat pump control system, the multi-mode process working medium system, such as noon mode and winter energy saving mode, can be designed for users to choose from according to different user needs, typical seasonal change characteristics, and daily temperature change rules.

• Optimized defrosting control design. Studies have shown that the main reason for the unsatisfactory performance of the unit during operation in areas with low temperatures and high relative humidity is the decrease in heating capacity caused by frost formation and defrosting of the evaporator. Therefore, effective defrosting methods must be used for timely defrosting [6]. At present, the defrosting method commonly used in air source heat pump is reverse circulation hot gas defrosting, and the automatic defrosting control method is particularly critical.

• Reasonable configuration of throttling device [8]. Using different capillaries, the performance of air source heat pump system in various environments is very different. When the ambient temperature is higher, the performance of thick and short capillaries is better. When the ambient temperature is lower, the performance of thin and long capillaries is better. In order to solve this problem, only the double capillary can meet the heat demand and solve the problem reasonably.

5. Conclusion

In this paper, the heat engine model and its application are analyzed, and it is concluded that some means can be used to improve the heat engine efficiency, and the heat engine efficiency is not unupgradable. Combined with the actual case analysis of air source heat pump, whether it is to design a variety of control modes, optimize defrost control, or configure throttling devices, the purpose is to reduce the impact of changes in ambient temperature on the efficiency of air source heat pump. From the two levels of open source and throttling, comprehensively improve the heating capacity to increase the temperature of high temperature heat sources, and reduce energy waste through design, so as to improve energy efficiency and reduce energy consumption.

However, this study also has some shortcomings: First, this study is a qualitative study without empirical analysis of large samples, and many indicators only stay in the qualitative description stage. Secondly, this study focuses on the current development of heat engine efficiency technology, and the economic benefit evaluation of each technology is still insufficient. Thirdly, this study has a general idea of the application and promotion path of heat engine efficiency technology, and the specific implementation suggestions are not rich enough.