1. Introduction

Although classical computers increase their ability to computation followed by Moore’s Law, they seem to reach their limitation contemporarily, i.e., hard to improve hugely as before. With the minification of their sizes, it is impossible to take the quantum effect out of consideration. Besides, to avoid the weakness of classic computers, scholars also propose some other ways such as crystal valves and quantum dots, where quantum mechanics still dominate [1]. Since the discovery of the concept of quantum, the subject has changed the cognition of the world and sped the creation of a large number of new technologies. Therefore, someone came up with the idea that connects quantum mechanics and computations to break through the limitation. In other words, researchers want to create a computer that is based on quantum logic initially to process information [1].

There are some differences between classical computation and quantum computation. According to Shannon’s information theory, the bit, the carrier of information, is widely used in the production and process of information with a binary algorithm. Similarly, the concept of a combination of quantum and bit—qubit—is coined to represent messages in quantum computation. A qubit is a unit vector in the vector space C², which is the superposition of |0⟩ and |1⟩ corresponding to bit 0 and bit 1, respectively. Besides, the transformations on qubits are unitary, different from the operations in classic. Moreover, the key to quantum information is quantum entanglement. Object to quantum mechanics, Einstein, Podolsky, and Rosen proposed a paradox, which accidentally introduced entanglement into physics [2], blooming quantum information.

Based on the former physical knowledge, Feynman et al. proposed the idea, which is considered as the beginning of quantum computers [3]. Feynman suggested a machine simulating physics directly and then give some basic thoughts about simulating time and simulating probabilities [4]. Afterward, from the reversible system, he gave some reasons that quantum computers can reduce the occurrence of entropy and irreversible interaction and the reduction of their size has no limit [5]. With many years of development, quantum information has achieved greatly in quantum computers, quantum communication, quantum cryptology, and quantum algorithm.

Quantum circuits and quantum gates play an essential role in quantum information. Quantum circuits are channels to transmit qubits and connect different quantum gates, showing the logic of the process, while quantum gates serve as the operation or transformation of qubits. Recently, quantum gates and circuits have gained ample accomplishments. Examination of the fidelity of quantum gates and improvement of fidelity of quantum gates can monitor and advance the accuracy of a quantum process [6-9]. Besides, the teleportation of quantum gates is another way to transmit messages prevalent for modularity and fewer errors [10]. This paper provides a brief introduction to the advantages of quantum bits, quantum circuits, and quantum gates and their future development, as well as pointing out the more cutting-edge scientific discoveries of today and linking them to possible future directions in the discipline. Besides, we also introduce the limitation and prospects of quantum information to urge further study.

2. Quantum Information

2.1. Quantum Bit

It is well known that in classical information theory, we use the bit to represent the carriers by which information is transmitted. A bit is a binary variable whose value is often written as 0 and 1. Therefore, in a classical computer, one can represent all information as 0 and 1 utilizing a binary algorithm, e.g., for an integer N we can represent it as

\( N=\sum _{k=0}^{n-1}{a_{k}}{2^{k}}\ \ \ (1) \)

The advantage of using binary for classical bits is that such data is ideally suited for storage in electronic devices [1]. An electronic circuit consists of two parts, wires, and gates, where the bits carry information in the wires and the bits are logically manipulated at the gates, a process that is the input and output of classical information [1]. In analogy to the carrier bit in classical information theory, for quantum information theory, this study will refer to the carrier of information as the quantum bit (qubit). As mentioned before, classical bits have only two states, either 0 or 1, whereas in quantum computing we use Dirac notation and represent quantum bits in a two-dimensional Hilbert space

\( |0⟩=[ \begin{array}{c} 1 \\ 0 \end{array} ],|1⟩=[ \begin{array}{c} 0 \\ 1 \end{array} ]\ \ \ (2) \)

The classical 0 corresponds to \( |0⟩ \) , and the state 1 in the classical corresponds to \( |1⟩ \) (here the requirement is that it should be orthogonal \( |0⟩,|1⟩ \) , i.e., mutually independent). There seems to be little difference between classical and quantum, but according to one of the fundamental assumptions of quantum mechanics: the principle of superposition of states, in quantum information the real state presented is in fact in the form of superposition of states (when not measured) \( |ψ⟩=α|0⟩+β|1⟩ \) , where α and β are complex numbers whose squares denote the probability of occurrence rate, respectively, and to satisfy normalization, there should be \( {α^{2}}+{β^{2}}=1 \) . In contrast, for the case with two quantum bits, four ground states \( |00⟩, |01⟩, |10⟩, |11⟩ \) are obtained by linear superposition [11]:

\( |ψ⟩={C_{00}}(|0⟩⊗|0⟩)+{C_{01}}(|0⟩⊗|1⟩)+{C_{10}}(|1⟩⊗|0⟩)+{C_{11}}(|1⟩⊗|1⟩)\ \ \ (3) \)

By analogy, for n quantum bits, we need a superposition of \( {2^{n}} \) basis vectors to get the state of the system. In contrast to classical bits, although the state of a quantum bit is not 0 or 1, in a mixed state, when we measure it, the mixed state eventually collapses to one of \( |0⟩ or|1⟩ \) and gives the classical value of 0 or 1 [12], but the quantum computer still has advantages in information storage and information processing that the classical computer does not have. For example, when we study a system of 40 spin one-half particles, a classical computer has to store \( {2^{40}} \) bits of memory, but a quantum computer only needs 40 quantum bits to solve this problem [13]; when we process the above information, we need to operate \( {2^{40}} \) several times to ensure that each state is acted upon, but a quantum computer only needs 40 operations. In addition, the entangled state of the quantum can bring many advantages to quantum computing [14].

For a more convenient and visual understanding of quantum bits, we generally rewrite equation (3) in the following form as

\( |ψ(θ,ϕ)⟩=cos\frac{θ}{2}|0⟩+{e^{iϕ}}sin\frac{θ}{2}|1⟩\ \ \ (4) \)

This \( |ψ(θ,ϕ)⟩ \) can then be considered as a vector pointing from the center of the ball to any point on the ball, and the operations performed on the quantum bits can be considered as rotations of this vector. This ball is then called a Bloch ball [1]. While the above is a mathematical analysis of the concept of a quantum bit, the next step is to describe the quantum bit from a physical point of view. A quantum bit is a two-energy quantum system, and in equation (3) we use \( |0⟩,|1⟩ \) , this set of basis vectors, which physically means that a quantum bit is represented by vertically polarized light and horizontally polarized light, as a two-energy system. For example, if one chooses the spin of an electron as the carrier of a quantum bit, it can be considered as the different spin directions of the electron. If we use the energy level state of the electron as the carrier, we can put the two basis vectors corresponding to the case where the energy level of the electron is in the ground state and the excited state respectively [12, 13].

2.2. Quantum Lines

A quantum line, also known as a quantum circuit, can be thought of as a combination of quantum logic gates and quantum bits, in which the effects of each quantum logic gate are understood to be applied in turn to the quantum bits (as shown in Fig. 1). The results of measuring the quantum line are measured using the principle of projection measurements.

Figure 1. A quantum line with two quantum bits.

The superposition principle can be demonstrated in quantum computing, which relies on the superposition of quantum states, i.e., the coexistence of some quantum states at one time, which is known as "Schrödinger's cat", and the superposition of quanta can be demonstrated by Young's double slit interference experiments on electrons [15] and Wheeler delayed selection experiments [16, 17]. Thereafter, it follows that the state of a computer of size n quantum bits can be expressed as \( |Ψ⟩=\sum _{i=0}^{{2^{n}}-1}{c_{i}}|i⟩ \) . Thus, in this quantum circuit, a computer is used as a quantum store to simulate both the vector of quanta and to store all possible states of quanta at the same time. The advantage of quantum computing is that the superposition of quantum states can be used to vectorize all the results of a quantum without requiring the researchers to input the results multiple times, and the results increase as the number of 2ⁿ quantum bits increases.

2.3. Quantum Gate

In contrast to traditional logic gates and gates and or gates, quantum computers use quanta to perform calculations that can exist in a superposition of "0" and "1" states, which are also dependent on the superposition of quanta and quantum gates are reversible. These quantum calculations rely on quantum logic gates, which are divided into two categories, single-quantum gates, indicated and multi-quantum gates. Single quantum gates are useful because they can switch the state of a quantum bit between "0" and "1", and can be written when the computational base is "0" and "1". "1" can be written in the as \( |Ψ⟩=α|0⟩+β|1⟩, |α{|^{2}}+|β{|^{2}}=1 \) . The difference between a multi-quantum bit gate and a single quantum bit gate is that it connects two or more quantum bits to perform the algorithm.

In this section, it is shown that single quantum bit gates and double quantum bit controlled non-gates are universal gates for quantum computing, i.e., all quantum gates can be represented by these two quantum gates. Let’s first show that the controlled U-gate can be disentangled into a single quantum bit gate and a controlled non-gate. For a controlled U-gate consisting of an arbitrary Missy-positive transformation U acting on a single quantum bit, it means that the quantum gate U acts on the target bit when the control bit is; if the control bit is, then no operation is performed on the target bit. Since any positive matrix requires the rows and columns of the matrix to be orthogonally normalized, we can assume that the correct transformation U is written in the following form.

\( U=[\begin{matrix}\frac{{e^{i(δ-\frac{α}{2}-\frac{β}{2})}}cos{θ}}{2} & -\frac{{e^{i(δ-\frac{α}{2}+\frac{β}{2})}}sin{θ}}{2} \\ \frac{{e^{i(δ+\frac{α}{2}-\frac{β}{2})}}sin{θ}}{2} & \frac{{e^{i(δ+\frac{α}{2}+\frac{β}{2})}}cos{θ}}{2} \\ \end{matrix}]=Φ(δ){R_{z}}(α){R_{y}}(θ){R_{z}}(β)\ \ \ (5) \)

where

\( Φ(δ)= [\begin{matrix}{e^{iδ}} & 0 \\ 0 & {e^{iδ}} \\ \end{matrix}]\ \ \ (6) \)

and \( {R_{y}},{R_{z}} \) are the matrices that rotate about z and y axes. It can be obtained that for any such matrix U, there are matrices A, B and C

\( A={R_{z}}(α){R_{y}}(\frac{θ}{2}), B={R_{y}}(-\frac{θ}{2}){R_{z}}(-\frac{α+β}{2}), C={R_{z}}(\frac{β+α}{2})\ \ \ (7) \)

Hence, \( ABC=I, Φ(δ)A{σ_{x}}B{σ_{x}}C=U \) . Therefore, one can use the route shown in the Fig. 2 instead of the controlled U-gate. It indicates that when the control bits are \( |0⟩ \) , the target bits remain the same as the initial state after passing through the quantum gate CBA, respectively. When the control bits are \( |1⟩ \) , target bits pass through the quantum gate respectively \( C{σ_{x}}B{σ_{x}}A \) , Re-use of logic gates \( Φ(δ) \) to eliminate the extra phase, we get the same result as if the initial quantum state had been transformed by U.

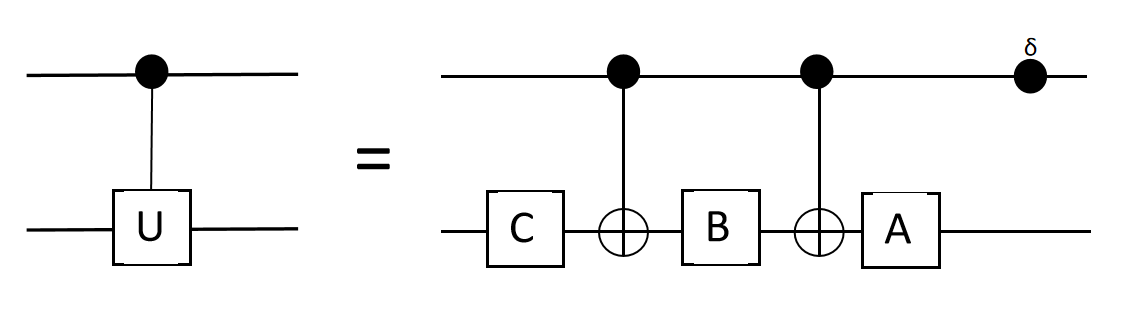
Figure 2. Unitary U can be composed of single quantum gates and 2-bit XOR gates.

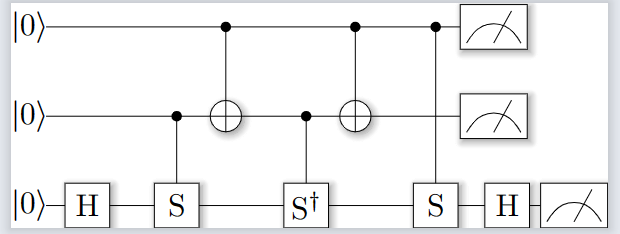
Figure 3. Toffoli gates can be composed of controlled non-gates, controlled U-gates, and Hadamard gates. The left is a Toffoli gate and the right is the alternative circuit, both drawn by ProjectQ.

Quantum Gate \( {C^{k}}-U \) denotes when the quantum states of all the control bits in the controlled line are \( |1⟩ \) , Only then is the change U operation performed on the target bit; only the presence of a quantum state of the control bit as \( |0⟩ \) , then no operation is performed on the target bit. In classical computing, \( {C^{2}}-U \) Gates, also known as Toffoli gates, are universal gates and as such have a very important role in classical computing. Likewise, it has a pivotal role in quantum computing. It can be shown that Toffoli gates can be composed of controlled non-gates, controlled U-gates, and Hadamard gates, as shown in Fig. 3. Here, S denotes

\( S= [\begin{matrix}1 & 0 \\ 0 & i \\ \end{matrix}]\ \ \ (8) \)

S and \( {S^{†}} \) both can be constructed with controlled non-gated single quantum bit gates Having obtained Toffoli's generic quantum gate construction method, it is possible to further generalize it with the help of Toffoli gates and auxiliary quantum bits to obtain any \( {C^{k}}-U \) gate both can be obtained using single-bit quantum gates and controlled non-gate constructions. For any unitary transformation acting on n qubits, we first use the decomposition formula proposed by Barenco et al. in 1995

\( {U^{(n)}}=\prod _{{2^{n}}-1}^{i=1}\prod _{i-1}^{j=0}{V_{ij}}\ \ \ (9) \)

the \( {V_{ij}} \) is to rotate \( |i⟩, |j⟩ \) following a 2x2 unitary matrix. The construction of \( {V_{ij}} \) can utilize the Gray code. The quantum state \( |i⟩ \) is transformed into \( |{i_{f}}⟩ \) state through a generalized gate, so that the Gray code of state \( |i⟩ \) is only one digit different from code of state \( |j⟩ \) . Then, \( {C^{k}}-U \) gate is used to rotate \( |{i_{f}}⟩ \) state and \( |j⟩ \) state and reversible transformations are operated for used states to restore them. Based on the above process, \( quantum gate{ V_{ij}} \) only acting on \( |i⟩ and |j⟩ \) is constructed [1, 18]. To put it in a nutshell, it is proved that single quantum bit gates and the CNOT gate are universal logic gates for quantum computing.

3. Applications of Quantum Gate

3.1. Examination of Fidelity of Quantum Gates

It is demonstrated that the information can be coded to the properties of particles, e.g., orbital angular momentum, path, and polarization. Subsequently, it is transmitted and measured along the quantum circuit where quantum gates lie and make operations to the carriers. Based on the process, quantum states and quantum gates are valuable resources for the spread of information. Before using the operations and carriers to compute or transmit, it is essential to examine whether they are satisfied our expectations [7]. Fidelity, a central concept to quantum information, provides a mathematical prescription for the quantification of the degree of similarity of a pair of quantum states, as well as for the examination of quantum gates between the theoretical gates and expected gates [6]. Nowadays, the examination has included: quantum state tomography, direct fidelity estimation, and efficient verification of quantum gates etc. [7].

3.2. Improvement of Fidelity of Quantum Gates

High-quality two-qubit gates with high fidelity are crucial for quantum information processing [8]. Currently, the decrease in the fidelity of quantum gates mainly comes from the following three reasons: imperfect control, non-ideal interactions, and decoherence which is the dominant source in the protocols [19]. For decades, many researchers have struggled for methods to hold high-fidelity gates. One of them is to introduce the idea of adiabatic into quantum gate operations due to the insensitivity of adiabatic characteristics. It is reported that a two-qubit-super adiabatic (TQSA) gate protocol based on parametric modulation enables a fidelity of 94.2% and even higher with higher coherence [7, 8]. Besides, there is a way that combines the conventional time-optimal quantum control strategy with dynamically corrected gates techniques constructing a unitary transformation which is coherence free. This protocol has been proven effective in theory and experiments [9].

3.3. Teleportation of Quantum Gates

With the rapid development of quantum computation, nowadays scientists have come up with a more effective and efficient method to deal with the noise and errors from the environment, i.e., modularity. The modular architecture is a distributed network of modules composed of small components and communicated by both the classical and quantum channels. A small component mainly consists of two parts: data qubit(s) that store and process information and communication qubit(s) that mediate the interaction between different modules. Adopting these circuits, one can isolate the process in the module and there will be less interaction between the different modules, which means the system will keep high efficiency even the scale expands. Initially, scholars realized the state teleportation of unknown quantum states between two modules. Expanding the technique, scientists conceive the teleportation of quantum gates similarly. The chosen gates can implement a unitary operation between two unknown states with a protocol without any direct interaction between the two data qubits. The process of teleportation of CNOT gate can be shown in Fig. 4. D1 and D2 represent data qubits while C1 and C2 represent communication qubits. The procedures are: (1) C1 and C2 are entangled by the quantum channel, (2) the CNOT gates entangle C1 and D1, C2 and D2 respectively, (3) measure C1 and C2, (4) give feedback to D1 and D2 after measurement [20]. It is demonstrated that the CNOT gate and the controlled-G gate are possible theoretically [10, 20].

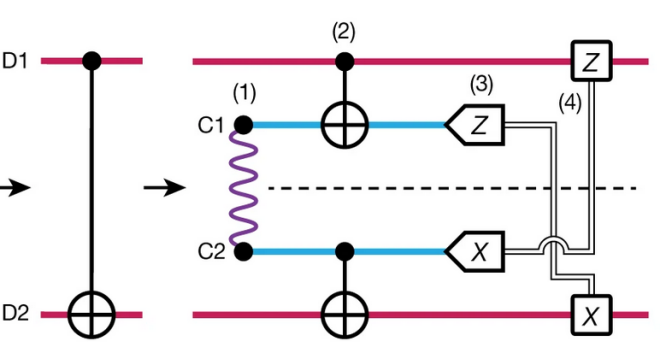
Figure 4. the brief process of teleportation of CNOT gate.

4. Limitations & Prospects

Although quantum information has achieved a multiplicity of accomplishments, it still faces some problems and limitations in quantum algorithms and quantum control systems, which simply means no operable application has been realized. From the software of computation, it is known that the computer needs algorithms to function on the import data then it can outport results in classic computers. Similarly, in quantum computers, people also need some algorithms specialized for quantum systems to do calculations or other operations. Algorithms including Shor algorithms, Grover algorithms, and variational quantum eigen solver algorithms have been proposed, but it requires more algorithms applied to quantum computers to realize practical quantum computation. Besides, quantum control systems are also required to improve, where the systems connect quantum algorithms and quantum physics systems. The main challenges of quantum control systems are prompt feedbacks to realize feedback control and a close connection between algorithms and physical systems [21]. Presently, many institutions and companies, e.g., Google and IBM have explored superconductivity-based, optical-based, and other methods-based quantum control systems.

From a short-term perspective, quantum computing can be implemented in quantum simulation, quantum optimization, and quantum-enhanced artificial intelligence. To be specific, compared with the function of approximation of nature in classical computers, quantum simulation is the most fundamental application to simulate the physical principles of nature radically and chemical processes precisely. The accuracy of modeling can be improved, and the efficiency of research and development in areas such as biopharmaceuticals and chemical materials can be enhanced. Hence, in the biomedical field, the middle and latter stages of drug manufacture require a large amount of data modeling and calculation, where very high computing power to analyze the molecular properties of the drug simulation is necessary. On this basis, quantum computers just have an advantage over classical computers. Therefore, quantum computing is a disruptive technological development with enormous potential value in both information science and the future strategic deployment of the resources that underpin quantum information science, which has been developed by leaps and bounds in recent years on all fronts.

5. Conclusion

In summary, we focus on quantum bits, quantum circuits, quantum gates, and their applications. The model of quantum computing has its origins in the Turi computer and is based on the theory of quantum mechanics, which has been verified by numerous experiments since the beginning of the 20th century. It differs from conventional computers in the way it uses storage in the form of quantum superposition states and computation through the evolution of quantum states, thus achieving a quantum computer that takes less time than a classical computer to solve certain computational problems. Due to the current limitations on the number of quantum bits available with current technology, the computation of medium-scale quantum gates may be difficult to achieve applications shortly. Although quantum computers have very many advantages, they can only perform quantum computations that do not require a large number of operations. In the future, quantum computing will have greater development in quantum algorithms, quantum simulation, and quantum system control, to realize the true application of quantum informatics. Overall, these results offer a guideline to learn the basic concepts about quantum information such as qubits, quantum circuits, and quantum gates. Besides, it is also beneficial for researchers to know the cutting-edge developments, promoting further knowledge of quantum information.