1. Introduction

1.1. Discovery of dark matter

Galaxies are the basic blocks in the Universe. Galactic clusters are where the abundance of galaxies is much higher than the cosmic void. In galactic clusters, a huge gravitational well keeps the galaxies bound. However, the galaxies in the clusters we observed seemed to not have enough mass to hold them together, implying the existence of dark matter. Dark matter cannot be observed directly but consists of approximately 30% of components in the Universe, was first discovered by scrutinizing the rotation curves of nearby galaxies [1]. The rotation curve is the circular velocity of a particle in orbit around the centre of the galaxy as a function of radius (the distance from the centre) [1]. By measuring the radial velocity from the Doppler shift of the absorption spectrum and observing material that is in the gravitational potential of the galaxy, we can calculate the velocity of objects moving around the centre of the galaxy.

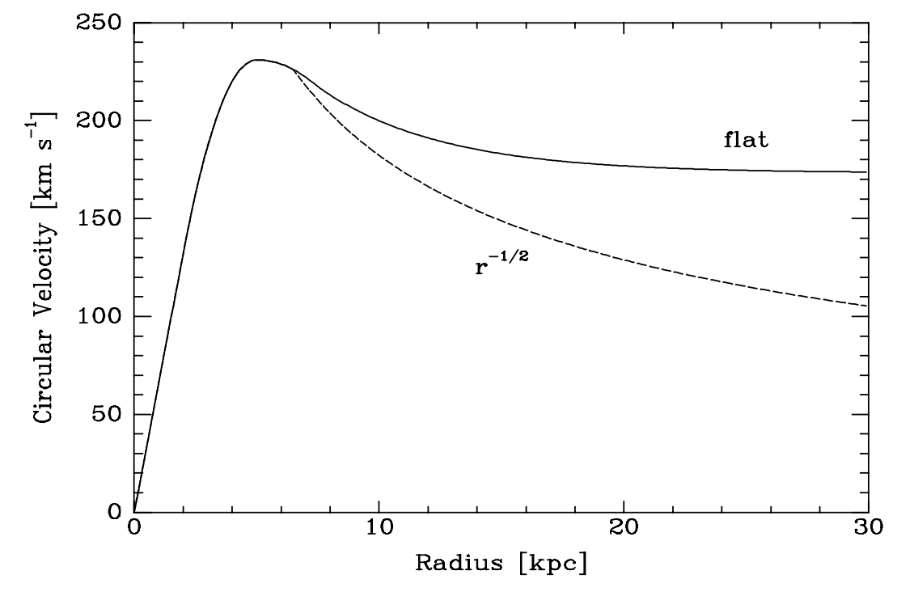
Figure 1. A schematic example of a galaxy’s rotation curve – The object’s circular velocity as a function of its radius. The “flat” rotation curve represents the measured rotation curve according to the data collected. The r^-1/2 rotation curve represents the predicted rotation curve according to the Keplerian fall-off [1].

The difference between the predicted rotation curve and the observed rotation curve shown in Figure 1 suggests the existence of unseen masses, now known as dark matter, providing deeper gravitational potential well in galaxies. The “flat” rotation curves are observed in almost all galaxies. For example, in our Milky Way, dark matter is about 80-90% of the Galaxy's mass, in order of 10¹² solar mass [1].

To further examine dark matter’s gravitational effect, astronomers’ study gravitational lensing. The brightening of stars/quasars when masses pass in their foreground. The compacted masses in galaxies effectively serve as a lens for objects in the background creating an optical image with a visible Einstein ring. When seen from optical telescopes captured in Figure 2, conspicuous arcs of gravitationally lensed distant background galaxies are imaged around the galaxies [2].

Figure 2. An optical image captured of the central region of the galaxy cluster Abell 2218. The arcs in the image are the gravitationally lensed image of distant background galaxies [2].

According to observation and plotting of the relative amplitude of fluctuations on angular scales, the geometry of our universe is flat, as \( {ω_{M}}+{ω_{λ}}=1 \) . Different values of \( {ω_{M}}+{ω_{λ}} \) would result in a variety geometry of universe shown in Figure 3. In modern cosmology, approximately 30% of the universe is made of matter, among them 95% is a dark matter [3]. The other 70% is known as dark energy.

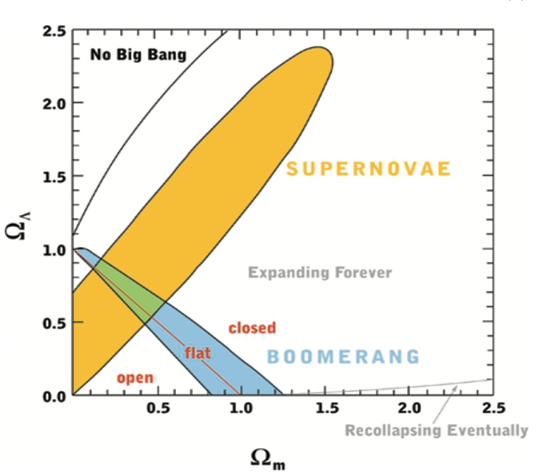
Figure 3. Data collected by BOOMERANG which shows the corresponding models of Universe to the combination of different percentages of matter and energy [3].

1.2. The nature of dark matter

Dark matter, things in our universe that do not emit waves of any frequency detectable, have a few possible natures and forms. The oblivious nature of dark matter meant that atomic gas, dust, stars, white dwarfs, electrons, and protons are impossible candidates for dark matter since they all emit observable wavelengths [1].

For instance,

• Atomic gas would radiate too strongly as 21 cm.

• Ionized gas would emit strong X-rays in thermal-free radiation.

• Dust would emit Infrared radiation and would produce a visible distinction with the background objects by the halo surroundings of other galaxies.

• Stars, whether it be main sequence stars or giant stars, they are all too luminous.

• Neutron stars, black holes, and white dwarfs are all the remnants of a star’s death which meant that they are metallically abundant and easily detected.

• Electrons and protons are ionized hydrogens that could also be easily detected.

After all the exclusion, there are a few candidates contending be to dark matter:

• Brown dwarf and planets (a type of Massive Compact Halo Objects) ranging from the size of Jupiter to 70 times the size of Jupyter emits little radiation [3].

• Massive neutrinos: neutrinos seem to have mass but it is not clear whether their mass can make up a significant component of dark matter [3].

• “Cold Dark Matter” is a category defined by astronomers as currently undiscovered diffused particles that are weakly interacting (just like neutrinos) [3].

After scanning the possibilities, there are mainly two categories for dark matter that are neither excluded nor arguably unlikely: diffused “Cold Dark Matter” and MACHOs [3].

1.3. MACHOs in the milky way

In 1986, astronomer Paczynski proposed an experiment to test if the dark halos in our Milky Way is composed of MACHOs. He assumed that dark halo would extend to Milky Way’s satellite galaxy, the Large Magellanic Cloud, at a distance of 50 kpc [1]. He calculated the probability of dark matter at the line of sight at any given moment, yielding one in a million stars in LMC should be significantly lensed by MACHOs within dark halos [1].

Further analysis by astronomers suggests that the crossing time scale of a solar mass MACHOs at half of the distance to the star would be 6 months. If the halo is composed of Jupiter-mass MACHOs, it would take 6 days [1].

The calculation is then contrasted with a 6 years of data collection monitoring 10 million stars: only 15 lensing events have been found for each experiment as opposed to 100 events expected. The significantly fewer amount of lensing events detected meant that MACHOs only contributed to a small portion of the dark halo in the Milky Way. Astronomer now suspects that the bulk of dark matter is made of cold dark matter rather than MACHOs [1].

1.4. Difficulty on detection of cosmic microlensing

Just like Paczynski’s problem of his samples, the crossing time of microlensing events at cosmic distance is at scales of months or even years. The further the distance between the lenses and the sample, the longer it takes the sample to cross its lens. Crossing time at the scale of days meant that the microlensing light curve is virtually impossible to be noticed. In addition, stars at cosmic are too faint with our given technology of telescopes. This greatly limits possible candidates for the light source to research.

In this paper, quasars, trillion times brighter than our sun, effectively serve as the background source. Quasars are bright enough for telescopes to measure the nuances of their light curve, and the radio-loud quasars also potentially possess superluminous motion, meaning a more observable crossing time. During data collection, a microlensing event whose crossing time is at the scale of days is observed.

This paper was organized as follows. In Section 2, the physics of microlensing and superluminous motion is introduced. In Section 3, the data collection process, the light curve of microlensing activity, and the implications of the light curve is discussed. A brief conclusion is given in Section 5.

2. Theory

2.1. Physics of microlensing

General relativity has predicted that space is curved due to the presence of MACHOs. In Schwarzchild’s metrics, from a distant observer's perspective, light is acquiring a speed less than \( c \) due to compact mass that forces the light to bend around the mass (just as the rarefactions predicted by Snell’s laws) [1]. Consider the following Geometric example of a light ray bending around a compact mass:

Figure 4. A geometric diagram of microlensing that demonstrates the situation when the Source (denoted as \( S \) ), lens (Shown through a dot), and Observer (a symbol of an eye) is aligned perfectly on the same optical axis [1].

In the microlensing geometry shown in Figure 4, denote the \( S \) as the light source, \( I \) as Image, \( α \) as the bending angle of the ray, \( b \) as the closest approach of the light ray to the compact mass, \( {D_{LS}} \) as the distance from the lens to source, \( {D_{OL}} \) as the distance of lens to object, and \( {D_{OS}} \) as the distance from the source to object. By symmetry (rotate the graph around the optical axis) the image of the source will deform into a ring known as Einstein angle ( \( {θ_{e}} \) ) [1].

By assuming that the gravitational field is weak, \( \frac{4GM}{{C^{2}}.b}≪1 \) , general relativity with thin lens approximation gives the bending angle \( α=\frac{4GM}{{C^{2}}.b}≪1 \) , so \( α \) is a small angle. In this case, we have \( b≪{D_{OL}} \) , implies \( {θ_{E}}≪1 \) .

Therefore:

\( SI=α. {D_{ls}}={θ_{E}}.{D_{os}} \) (1)

Substituting \( α=\frac{4GM}{{C^{2}}.b} \) for \( α \) , with \( b= {R_{E}}= {D_{ol}}.{θ_{E}} \)

\( \frac{4GM.{D_{ls}}}{{C^{2}}.{θ_{E . }}{D_{ol}}}={θ_{E}}.Dos \) (2)

Isolating \( {θ_{E}} \) :

\( {θ_{E}}={(\frac{4GM.{D_{ls}}}{{c^{2}}.{D_{ol}}.{D_{os}}})^{\frac{1}{2}}} \) (3)

This equation is the main equation used in the project.

2.2. Microlensing in cosmic distance

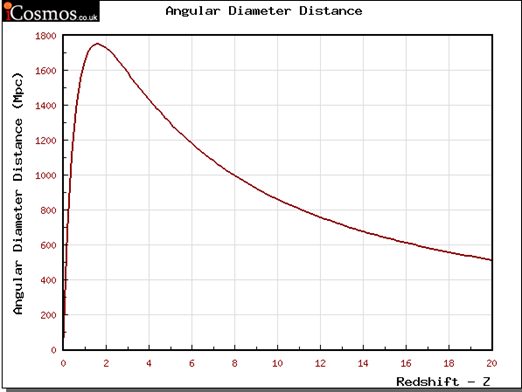
Figure 5. The angular diameter distance as a function of redshift.

However, a Euclidean plane isn’t accurate in calculating the distances in this project. In the cosmological model, angular diameter distance is used in calculations. Angular diameter distance is defined as the ratio of an object’s physical transverse size to its angular size in radians. This distance converts the angular separation in telescope images into proper separation as the source. Figure 5 suggests that distance does not increase indefinitely at the redshift increases, it also turns over at \( z \) ~1. Therefore, more distant objects actually appeared smaller in angular diameter distance [1].

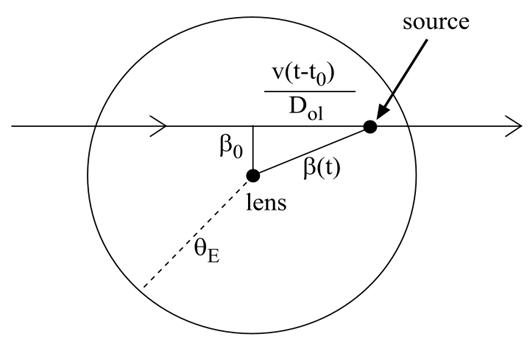
Figure 6. Geometry of Microlensing Events allowing astronomers to derive formulas from it.

Figure 6 illustrates the microlensing in the observers’ perspective (with the Einstein ring \( {θ_{E}} \) indicated and a source that is projected behind the lens). The source moves at a constant traverse velocity with its closest approach to the lens \( {β_{0}} \) . From the Pythagorean theorem \( β(t) \) can be established [1].

Astronomers yield the theoretical light curve model for microlensing:

\( u(t)={[u_{0}^{2}+\frac{{(t-{t_{0}})^{2}}}{{τ^{2}}}]^{1/2}} \) (4)

where \( {u_{0}}=\frac{{β_{0}}}{{θ_{E}}} \) , \( τ=\frac{{θ_{E}}{D_{ol}}}{v} \) .

Since \( {u_{0}}=\frac{{β_{0}}}{{θ_{E}}} \) , when \( u \) = 1 (the source is on the Einstein ring), the source would be magnified by 34%. The light curves caused by difference values of u have been illustrated in the previous figure.

2.3. Superluminal movement of quasar jets

Superluminal movement refers to a celestial object that appeared to possess a speed faster than \( c \) due to the difference between the actual distances travelled by the object and the measure of its proper motion [4]. Figure 7 suggests that even though 4 years have elapsed, the quasar’s jet is 27 light years away from the quasar [5].

Figure 7. The superluminal motion observed in the jet of a quasar.

Figure 8. This Diagram shows a celestial object moving from position \( A \) at \( {t_{1}} \) to position \( B \) at \( {t_{2}} \) . As the observer ( \( O \) ), the proper motion of the object CB is observed [1].

The velocity of the quasar to an observer derived from geometry of Figure 8:

\( {V_{T}}=\frac{ϕ{D_{L}}}{δ{t^{ \prime }}}=\frac{v.sinθ}{1-βcosθ} \) (5)

The ratio of apparent velocity and the speed of light:

\( {β_{T}}=\frac{{V_{T}}}{c}=\frac{β.sinθ}{1-βcosθ} \) (6)

When \( θ \) is a small angle and \( β \) approaches 1 ( \( v \) approaches \( c \) ), then \( {β_{t}} \) > 1, and super luminous motion is a kind of apparent phenomenon, but not a physical velocity.

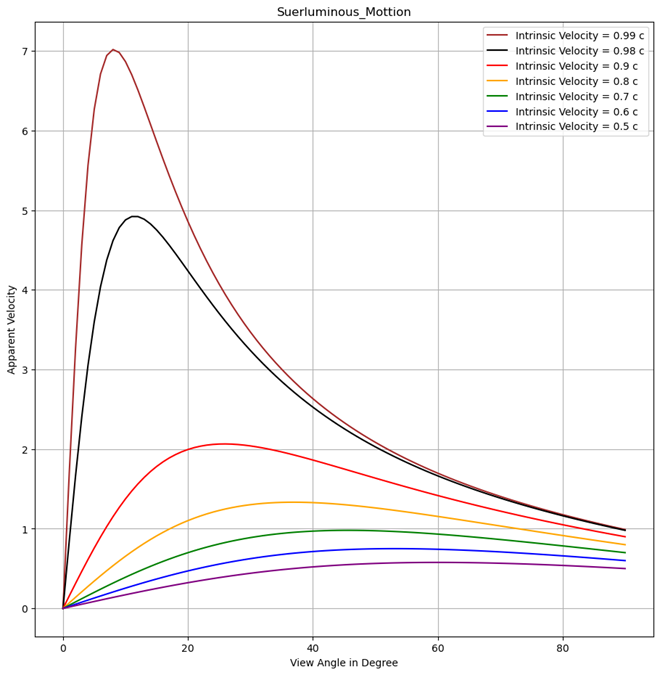
Figure 9. Superluminal motion as a function of intrinsic velocity and the view angle. For each intrinsic velocity of the object, there is a corresponding optimal view angle that maximizes its apparent velocity. For example, an object moving at an intrinsic velocity of 0.99c cannot be observed at a velocity higher than 7c.

At each intrinsic velocity, from 0c to 10c, there is an optimal view angle that maximizes its apparent velocity observed by the observer shown in the turnovers of the graph in Figure 9. For instance, an object with an intrinsic velocity of 0.99c can be observed as an object moving at the speed of 7c seen at roughly 10 degrees. The relative location of where the Earth and the relative speed between the Earth and the Quasar plays a key role in viewing the superluminous motions of quasars.

3. Analysis of WISE J182159.47+681843.0

3.1. Collection of WISE light curve

The Wide Field Infrared Survey Explorer was launched by NASA to image the entire sky in infrared. The survey provides data in different light frequencies, confirming whether the light variability is an intrinsic or an external factor. During research two isolated microlensing events toward quasar WISE J182159.47+681843.0 is discovered during research.

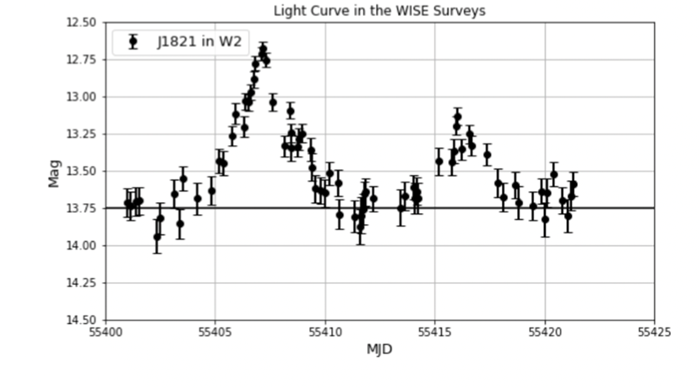
Figure 10. The graphs above are the light curves obtained from WISE Survey from two different wavelengths of light (W1 and W2). In the plot, the two light curves look similar, both possessing two separate peaks of magnitudes. The similarity suggests that the microlensing is not caused by intrinsic factors but rather something extrinsic – a microlensing event.

After model fitting this graph yielded from WISE survey presented in Figure 10, estimation of the crossing time of both microlensing activities can be obtained, allowing us to estimate the diameter of the Einstein ring and then their masses.

3.2. Identify the location of gravitational lens

After some research about this miraculous double microlensing event, a picture has been captured that suggested a galactical cluster at the foreground of the quasar.

Figure 11. This picture is adapted from RXJ1821.6+6827: A cool cluster at \( z \) =0.81 from the ROSAT NEP survey by Gioia et al [6].

In Figure 11, the redshift and the location of the quasar and the galactical cluster are labelled clearly on the graph, it is high possible that the candidate of the lens in among the galactical cluster. But more analysis is needed to narrow down the mass of the lens to determine whether the lens has a solar or planetary mass.

3.3. Analysis of WISE light curves

Using the theoretical light curve model for microlensing to fit the observed light curve by WISE, the variable of the microlensing geometrics can be determined.

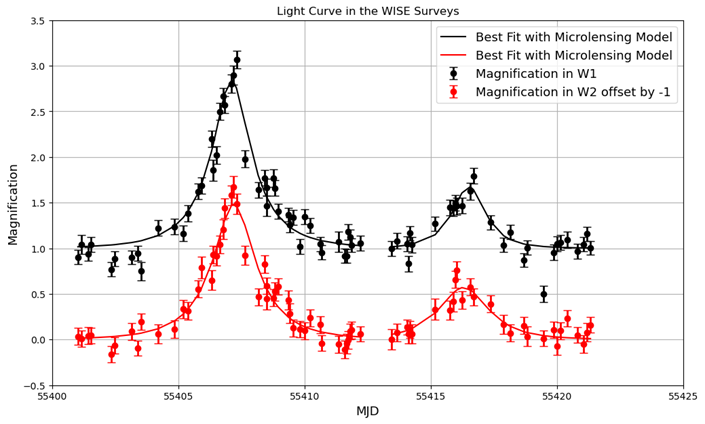
Figure 12. Light curves yielded from both W1 and W2, with best fit models for microlensing events.

From the model fitting and yielding Figure 12, estimation of the crossing time of the lens is made (about 2 days for the left event and 1.3 days for the right event). The following equation can be used to establish the relationship between the lens's mass and the lens's velocity.

\( {R_{E}}={(\frac{4GM.{D_{ls}}}{{c^{2}}.{D_{ol}}.{D_{os}}})^{\frac{1}{2}}} \) (7)

\( M=\frac{R_{E}^{2}{c^{2}}}{4G}.\frac{{D_{L}}}{{D_{ls}}{D_{s}}} \) (8)

R = Crossing time × velocity

So, \( M= \frac{(v × t) {c^{2}}}{4G}.\frac{{D_{L}}}{{D_{ls}}{D_{s}}} \) .

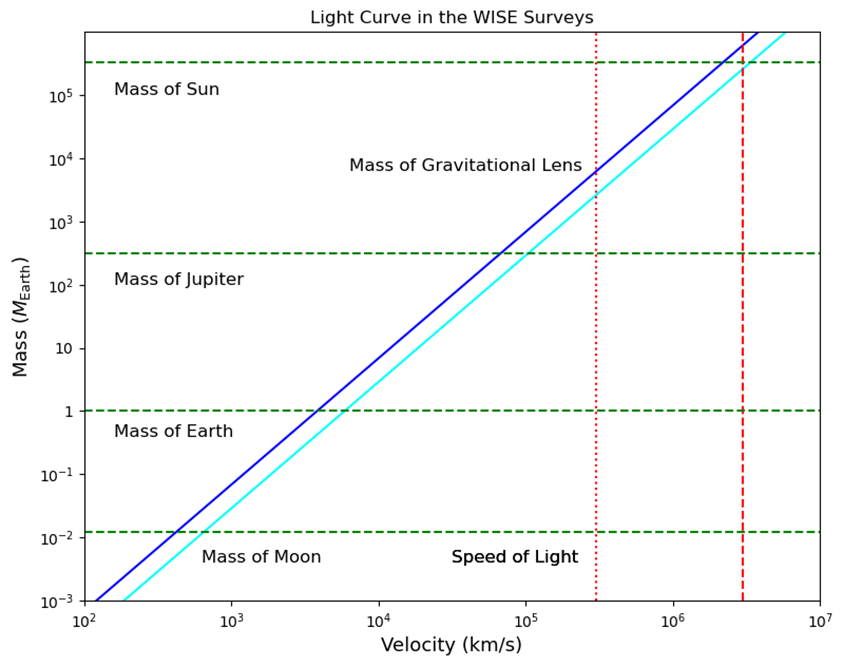
Figure 13. The mass of two lensing objects dependent on the relative velocity (blue and cyan slant lines). The mass of the Moon, Earth, Jupiter, and Sun is labelled by dashed green lines. The speed of light and the 10 times the speed of light is labelled by vertical red lines.

By estimating the crossing time from the WISE light curve as 2 days and 1.3 days, the calculation yields the following graph in Log space.

3.4. The nature of the lensing objects

The graph of the mass and velocity of the lens (presenting in Figure 13) yielded from assuming that the lens is within the cluster in the foreground suggests that the lens is in the order of either solar mass or planetary mass. The mass depends on whether the lens is in superluminous motion or not. Unfortunately, we cannot measure the traverse velocity of the lens since we cannot receive any forms of the wavelengths of light from the lens.

Nevertheless, by assuming different velocities of the lenses and finding of the possible relationships between them can provide insights of what the lens in the case of J1821 is. The separation of the microlensing events is around 10 days. If the velocity of both lenses is around 5000 km/s (meaning that the mass of the two lenses is at the order of planetary mass), the distance between the two lenses is 7 AU. The distance of 7AU apart meant that the two planets would likely be in the same solar system.

But what if the lenses are solar masses, meaning they have a velocity of around 10⁶ km/s. The calculation yields that the two stars are 100 AU apart. Two stars with a mere distance of 100AU mean that they are gravitationally bounded; therefore, it would be a binary system. Admittedly, assumptions of lenses’ location, velocity, and mass are made in order to acquire this information. Astronomers now can keep track of the region and potentially map out a new solar system in deep universe.

4. Conclusion

In this project, I discovered two isolated microlensing events toward quasar J1821. The WISE light curves in W1 and W2 bands are almost identical in magnification. The crossing times for the two events are in the scale of the day, the lenses are probably a star or sub-stellar object. A galactic cluster with a redshift of 0.81 lies in our sight of view quasar consolidates my conclusion. The galaxies in galactic clusters are a possible host of the lenses. In this case, by probing the relationship between the distance separating two distinct microlensing events, it is positive that a solar system lies in that particular area of deep space. The quantity of discovered single microlensing events is minuscule. The double-microlensing events discussed in the paper are the only events astronomers have recorded. The findings of implications from the light curves proved the effectiveness of studying microlensing activities as means of learning about stars, planets, and dark matter in deep space.