1. Introduction

The large number of observation results that violate the basic Newton’s laws have suggested the existence of dark matter (DM). DM is assumed to take up about 85% of the universe’s mass, and it might have unavoidably acted a critical role in affecting the development of galaxies and stars. Whereas, the nature and characteristics of DM still remain unsolved, and it is one of the most important frontiers in astrophysics.

Primordial black hole (PBH) was first proposed by Zel’dovich and Novikov. Then in 1995, Bousso and Hawking examine the probability of PBHs in an ordinary Friedman universe and a universe containing PBHs [1]. Theoretically, there’s no collision happens on PBHs, and they are also non-relativistic. Thus, PBHs are recognized as one of reliable candidates for DM. They were formed during the earliest stages of the universe, assumingly through the collapse of large energy density fluctuations [2], instead of through the collapse of stars as normal black holes, and this formation process can be described with a three-zone model (seen from Fig. 1) [3]. The non-evaporating PBHs of substantial massive might cause effects on the universe that can be detected, such as abnormal distortion of cosmic microwave background (CMB), special gamma ray bursts, the constitution of stars, or the formation of DM [4].

From the detectable signals listed above, scientists have found some cosmological data that indicates the existence of a PBH. In 2016, LIGO (Laser Interferometer Gravitational-Wave Observatory) laboratory observed several gravitational waves emission events from two merging black holes, and intense discussion followed. Carr focused on PBHs within mass ranges of \( 1{M_{⊙}} \lt M \lt {10^{3}}{M_{⊙}} \) , \( {10^{20}}-{10^{24}}g \) , and \( {10^{16}}-{10^{17}}g \) , discussed their formation mechanism and their possibility of being dark-matter candidates. He discovered that scenarios of \( 1{M_{⊙}} \lt M \lt {10^{3}}{M_{⊙}} \) and \( {10^{20}}-{10^{24}}g \) still yield all dark matter, and he also formed the Carr-Hawking collapse model [5]. In this model, he explained that a PBH is formed only under the condition when the disturbance enters the horizon lies within \( w={δ_{c}} \lt {δ_{H}} \lt {δ_{max}}=1 \) , where \( {δ_{H}} \) is the density perturbation and \( p=wρ{c^{2}} \) is assumed [4]. In another study, analyzed with N-body simulations, the formation and disruption process of PBH pairs are in good agreement with the gravitational waves’ emission events, which backs up the theory that PBHs contribute to a great proportion of dark matter in the universe [2]. Combining the finding of LIGO and Plank data, Lu Chen et al. construct limits for the abundance of PBHs and with the result implicate events rate of PBH binaries mergers, which is approximately \( 5 (Gp{c^{-3}} y{r^{-1}}) \) for \( {M_{bph}}=10{M_{⊙}} \) and 2000 \( (Gp{c^{-3}} y{r^{-1}}) \) for \( {M_{bph}}=2{M_{⊙}} \) [5].

However, still, the PBHs’ existence hasn’t been directly spotted or confirmed. Scientists from all over the world have been trying to get direct observation evidence of PBH through sky survey projects such as SGARFACE [6]. This experiment further narrows down the constraints for PBHs. More systems like EGRET and FERMI are trying to detect the gamma ray radiation from the evaporation of PBH with \( {M_{pbs}}≤7×{10^{12}} kg \) . Thus, to assist the search for PBHs, this paper aim to point out some possible coordinates of where PBHs have existed. One uses the more recently and delicately designed THESAN simulations to track and map the DM density field in early universe. By filtering out the areas with denser DM distribution, one can get the observation goals that may increase the possibility of discovery and reduce the workload to minimum at the same time.

Figure 1. Taking confidence level of 95%, the upper boundary on the abundance of PBHs in DM and shows relationship between \( {M_{bph}} \) and \( {f_{pbh}} \) . The black solid line indicates the result from calculation and the grey line corresponds to the constraints from data.

2. Basic descriptions of THESAN

2.1. Project description

THESAN is a set of large volume ( \( {L_{box}}=95.5 cMpc \) ) radiation hydrodynamic simulations that, with unparalleled physical fidelity, self-consistently portray the reionization process and the galaxies responsible for it [7]. It was built aiming to understand how universe works especially during the first billion years following the Big Bang. In particular, it seeks to shed light on how galaxies and the intergalactic medium interacted during the Epoch of Reionization. The design strategy enables previously unattainable observations of both cosmic reionization and galaxy formation processes at the same time by incorporating the successful IllustrisTNG galaxy simulation framework with non-equilibrium heating and cooling, self-consistent radiation transport, realistic ionizing sources such as binary star systems and active galactic nuclei, as well as a model for cosmic dust genesis, evolution, and annihilation. It also has a number of medium resolutions used to investigate adjustments in the physical model, including research of numerical convergence, the dependency of source escape fraction on galaxy mass, and alternative dark matter models. Thus, with the large amount of data and models support, the system’s capable of doing complex and accurate simulation of early universe. Since the capability of current telescopes is limited, the numerical simulations can provide more controllable and approachable map of the universe as a supplement to observational data for astrophysicists.

2.2. Improvements compared to previous system

The numerical resolution of THESAN exceeds that of earlier simulations of similar volume. It takes galaxy formation models to yield physical characteristics that are consistent with observations of the present universe [8]. Such strategy is ambitious yet necessary to further our comprehension. The THESAN simulations carefully take into account processes invulved in the evolution of the universe, including rapid gas cooling brought on by cosmic expansion, structure formation triggered by the growth of dark matter overdensities, galaxy formation as rarefied gas collapese into the central regions of DM halos, and the emergence of complicated landscapes within the first billion years.

Table 1. Simulation of THESAN-HR suite.

With the hybrid Tree-PM apprach, gravity is solved. With the quasi-Lagrangian Godunov method, hydrodynamics is solved [9]. To carry out these simulations, SuperMUC-NG machine at the LRZ, one of the largest supercomputers in the world, is used. It employs approximately 60,000 processors, working simultaneously in parallel, for roughly 30 million hours of continuous calculations. THESAN simulations additionally take into account the cosmic dust, making it even more distinctive in the context of astrophysics simulations. Recently, dust reprocessed light has developed into a potent technique for examining the characteristics of the first galaxies. It is fast supplying plenty of knowledge about the early Universe's circumstances. Thus, self-consistently imitating this component is crucial for us to test our understanding of the early galaxies with prospective data from stronger observatories, even if dust modelling in simulations is a young technique.

3. Simulation sets

Due to the improvements made by THESAN simulations mentioned before, one employed THESAN-HR suite to simulate and map the distribution of DM in early universe. The applied simulations are listed Table 1 provides a summary of the simulations' specifics and numerical parameters. At the initial redshift of \( {z_{in}}=49 \) , with the Lagrangian perturbation theory of second order and the Gadget-4 code, the initial conditions are produced [8]. One employs the same linear matter power spectrum produced by Camb, which was also used in the IllustrisTNG simulation and the fiducial THESAN simulations, for the CDM model. Besides, as shown in Table 1. The models in the suite provide reduction in the linear matter power spectrum of low scales. They may have non-trivial effects on early structure developing.

For the WDM model, the DM particles’ free streaming brings cutoffs to the disturbances of density field at low scales. At the circumstance of thermal relic WDM, the transfer function is stated as

\( T(k)=(1+{(ak)^{β}}{)^{γ}} \) (1)

where \( β=2v \) , \( γ=-5/v \) , \( v=1.12 \) , and the characteristic scale of the damping is controlled by \( α \) [9]. When the linear WDM suppression reaches 1/2 in terms of matter power w.r.t. the ΛCDM case, the half-power wavenumber can be roughly calculated as

\( k_{1/2}^{WDM}≅22h \) Mpc \( { ^{-1}}(\frac{{m_{WDM}}}{3keV}{)^{1.11}}(\frac{{Ω_{DM}}}{0.25}{)^{-0.11}}(\frac{h}{0.7}{)^{1.22}} \) (2)

where \( {m_{WDM}} \) represents the WDM particle’s mass and \( {Ω_{DM}}≡{Ω_{0}}-{Ω_{b}} \) represents DM’s cosmological abundance [9]. One takes \( {m_{WDM}} \) = 3keV, which is of interest for the explanation of the 3.55 keV X-ray from the center of galaxies and is at the boundary of observational constraints [9]. For the IDM model that features DAOs, the model in the ETHOS framework will be taken. Two parameters, wavenumber of the first acoustic peak, \( {k_{peak}} \) , and amplitude of the first acoustic peak, \( {h_{peak}} \) , mainly controls the transfer function in DAO model. One uses the parameters \( {k_{peak}} \) = 40 ℎMpc \( { ^{-1}} \) , \( {h_{peak}} \) = 1. In this instance, the first damping wing’s half-power wavenumber in the power spectrum is

\( k_{1/2}^{sDAO}={k_{peak}}/2.5≅16hMp{c^{-1}} \) (3)[9]

4. Simulation results & analysis

Each panel has a zoomed-in view of the buildings surrounding the enormous halo in the upper left corner. Fewer low-mass haloes and filamentary structures are developed, because of the decreased small-scale power spectrum in models of altDM. Due to the DAOs, the sDAO model exhibits residual turbulence at tiny scales. With a single dampening of the power spectrum, it differs slightly from the WDM and FDM models. While a few small-scale structures can still emerge, the sDAO's overall density field is flattened.

With the initial conditions stated in part 4.1, this study runs the simulation suite. Using the fiducial THESAN physics, the simulations produced the DM density fields and are displayed in Fig. 2. Runs with homogeneous UVB produce nearly same DM distributions, which are displayed in Appendix A of Ref. [9]. Photographs of DM surface density maps at z = 6 in various models specified in Table 1 are provided in Fig. 2. In the lower panel, the column density map of neutral hydrogen at z = 6 in the simulations is shown. The camera position and the slice of volume visualized are kept the same as upper right left panel of Fig. 2. From the DM density field at z=6 that have been published by THESAN simulation; one finds DM halos where the DM density’s especially high. The total mass of all substances and particles bound by gravity defines halo mass, and THESAN-HR suite permits the accurate prediction of the halo characteristic, which is around 5× \( {10^{7}}{M_{⊙}} \) [9]. Since the PBHs are results of fluctuation and collapse happened at areas of extremely high density, these halos would indicate places with higher possibility of where a PBH might have been formed.

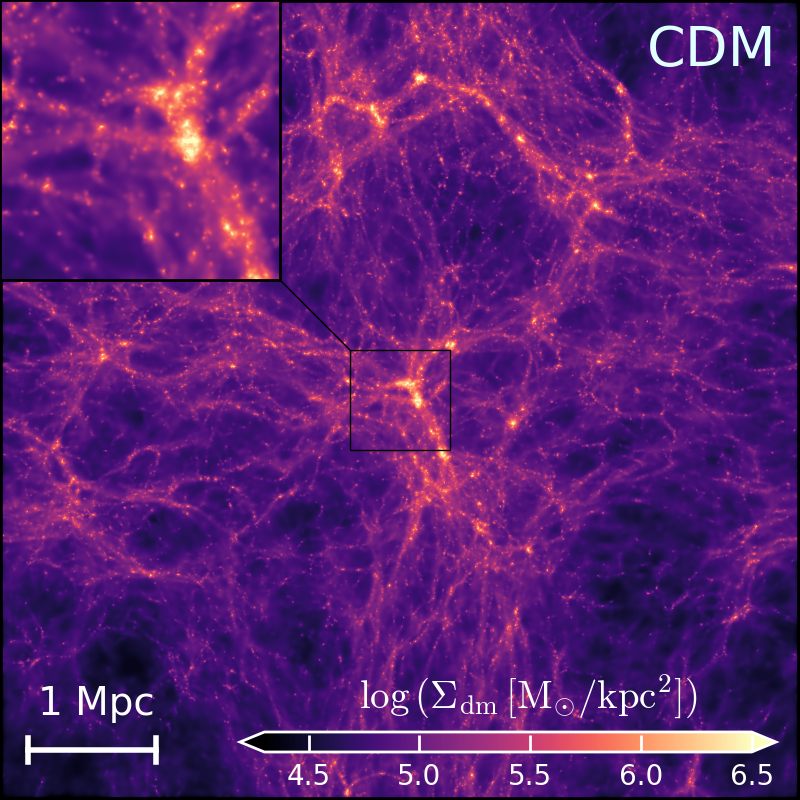
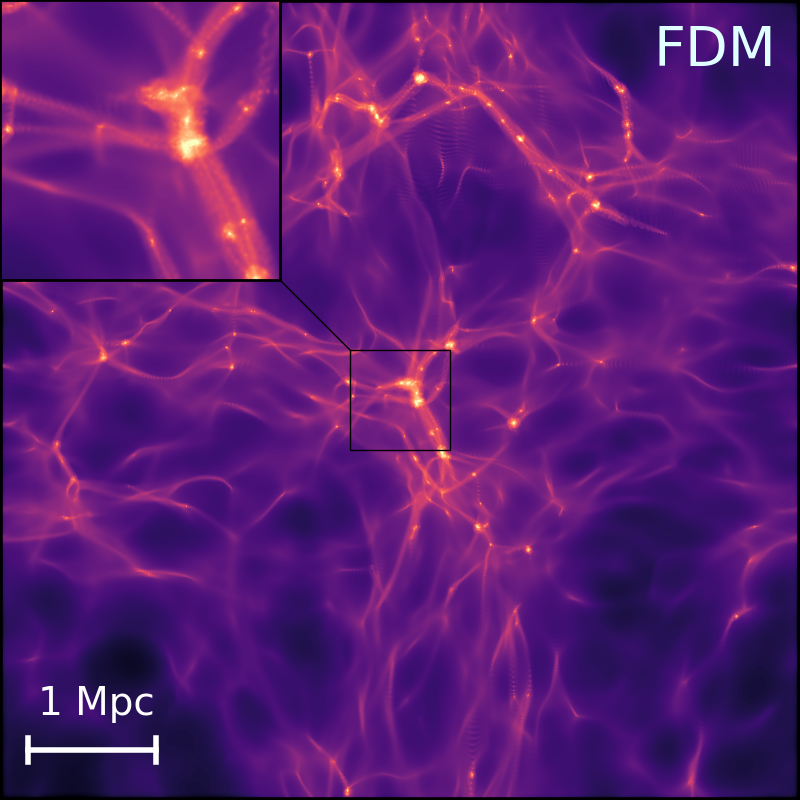
Figure 2. The DM density field from the simulations [9].

5. Limitations & prospects

Since the simulation data from THESAN that scholars have access to are still limited to only a few papers, the data analyzation isn’t that ideal. From only the DM density field at z=6 included in [9], one can’t observe the change in distribution of DM density. The coordinates of DM halos indicated in the maps within panorama universe is unclear, so one can only obtain the relative position of these dark matter halos. Thus, it’s hard for us to establish more systematical, representative, and accurate model for the indicators of PBHs. Also, only through simulation systems, our determination for universe at high redshift is unavoidably.

It is hoped that in the future, with more data released by THESAN simulation and corrections continue to be made, scholars will get more accurate estimator for the positions of possible DM halos. It is hoped that the further released data will include more complete parameter for the measurements of coordinate, density, or mass distribution. In addition, direct observations are of course more reliable or better than computer simulations. With larger number of parameters being collected from all telescope’s observational tasks, a more accurate image for universe at its origin will be graphed with models like Einstein’s field equations together with perfect fluid and state equation, combined with gravitational constants G and cosmological constant Λ [10].

6. Conclusion

In summary, the formation mechanism of primordial black holes suggests that the PBHs are possibly from collapse of large density fluctuations in early universe, such as a first-order phase transition or in some curvaton scenarios. Thus, this study provides a way to use dark matter density map and determine the possible coordinates where PBHs formed. This paper uses the THESAN system to display the condition at early universe. This study describes the basic principle and goals of THESAN and introduce its advantages over other prior simulation systems on describing the universe at reionization decades. This study set the initial conditions for DM density field simulation with the appropriate suites, and one successfully acquires the simulation data from THESAN system for DM density field at z=6 of partial early universe. Several DM halos are displayed in the DM density maps, and they are defined as indicators for PBH formation. This method of determination possible coordinates will offer us a series of places to be observed or detected preferentially, and thus might raise the efficiency for the search of PBHs.