1. Introduction

Cryptography is the process of allowing the sender and receiver to securely communicate and deliver their messages. Due to the fast development of the Internet, it is easy to leak users’ data without knowing it [1]. Thus, cryptography helps secure the data and information from plain text. One major category is Classical Cryptography. It includes the ciphers that are before 1950 and every Classical Cipher is broken. There are three components in a cipher. The plaintext, key, and ciphertext.

There are two types of keys, public and private keys. The public key is used to encrypt the data and messages, and it is shared between the sender and receiver. The private key is used to decipher data and messages [1]. The pair of a public key and a private key can complete the whole delivery process. Data is encrypted with a public key by the sender and the receiver can only decrypt with the corresponding private key. There are three algorithms in secret key encryption (SKE), key generation algorithm, encryption algorithm, and decryption algorithm. The key generation algorithm needs no input and outputs a key. The encryption algorithm takes the input as the message and a key. It outputs a ciphertext. The decryption algorithm takes the ciphertext and a key as input and then outputs the original plain text.

To test whether a cipher is secure enough, the access needs to be controlled with only the sender and receiver. Other people cannot access the message so that the information will not leak out. Also, during the sending process, there should be no loss or modification of information after the sender has sent it. What is more, authentication is important as the user's identity needs to be checked. Otherwise, any person can access the information [1].

The main theme of this essay is to analyze and organize Classical Cipher. Classical Cryptography can be classified into three categories, Substitution cipher, Polyalphabetic Substitution Cipher, and Transposition cipher. Substitution Cipher has an encryption algorithm to substitute the original letter with another letter. Polyalphabetic Substitution Cipher is to encrypt the plain text letter through groups of letters or words. A transposition cipher is to change how the letters in the explained text are arranged without changing what they are. This essay includes several examples of each category. Substitution cipher contains the Caesar Cipher and Simple Substitution Cipher. Polyalphabetic Substitution Cipher includes Vigenere Cipher. Transposition cipher consists of Scytale and Rail Fence Cipher. The meaning of this research is to make a better record or catalog of the history of Classical Cryptography. Then understanding Classical Cryptography can be more systematic.

2. Substitution Cipher

2.1. Caesar Cipher

Caesar Cipher is one of the earliest known cryptographic systems. Around 50 BC, Julius Caesar was proposed to send some vital secret messages to his army. He wrote to Marcus Cicero by shifting every letter 3 steps along the alphabet. This means that A is encrypted to D, B is encrypted to E, and X is encrypted to A. Then this type of cipher is then named Caesar Cipher. [2]

The main principle of the Caesar Cipher is to shift each character with a definite shift number. In the Caesar Cipher, the key is the shift number. Moving each character forward by the shift number can encrypt the text. Take shift number 5 and the short sentence "See you tomorrow" as an example. Just as shown in Figure 1, shifting the letter S with five steps forward will result in X. Letter e will be enciphered to j. Then the word See can be encrypted as Xjj. For the term you, the letter y will be shifted to d. Letter o will become t. Letter u will be z. Then the word you will become dtz after Caesar Cipher. By repeating this process, the encrypted text will become "Xjj dtz ytrtwwtb. " For people who plan to steal the encrypted text but without the key, what they can see is just some random letters that make nonsense. The ciphered text "Xjj dtz ytrtwwtb" and shift number five can also decrypt the cipher. Shifting the letter 5 steps backward will get the original text.

Table 1. Caesar Cipher with shift number 5.

In total, there are only 26 possible keys for Caesar Cipher. All characters have 26 possibilities for cipher results. Compared to other types of ciphers and rules for keys, the total number of possible keys needs to be bigger. There are several ways to break the Caesar Cipher. One way is to try every possible key. Still use the example mentioned above. Try the shift number as 1. Then the word Xjj may be encrypted from Wii, which is not a common English word. Shift number 1 is not the correct number. Then try some other shift numbers. The number 2 gets the result Vhh. Shift number 3 gets the word Ugg. For shift number 4, the result is the word Tff. Until it gets to shift number five, the word Xjj shows a common English word, See. There are possibilities that the real shift number is 2, 3, or 4. This is because VHH is a name for a type of antibody, UGG is a brand name, and TFF may be an abbreviation for a special term. These three words may be part of the original text and the word Xjj is being encrypted from them. To exclude the possibilities of shift numbers 2, 3, or 4, it is necessary to check the other words "dtz ytrtwwtb" using the same shift number and trace backward. Then it is obvious to find out that only shift number 5 can be used to decrypt the whole text into a sentence that people can read.

Another way to break the Caesar Cipher is to use the frequency analysis of English letters. In the post titled English Letter Frequency Counts by Peter Norvig [3], his research result shows that the letter e has the highest frequency in English. Thus, in a passage or a paragraph that was encrypted by Caesar Cipher, guess the letter that has the highest frequency in the passage as enciphered by e. Then count the shift number between them. Try the shift number on other letters and see if the shift number works. Take "Xjj dtz ytrtwwtb" as an example. The letter with the highest frequency in the text is t as it appeared four times. Make the letter t enciphered by the letter e. Then the shift number should be 15. The result sentence is "Iuu oek jecehhem". This is clearly the wrong sentence. Then try the letter w because it appears twice. The shift number needs to be 18 so that the letter e can be encrypted to the letter w. "Frr lbh gbzbeebj" is the result sentence but it is wrong. Then try the letter j and the shift number should be 5. By tracing backward, the original text appears as "See you tomorrow".

Caesar Cipher is classified as a type of substitution cipher because it follows the principle of substituting a letter from the original text for another. The key for Caesar Cipher is named shift number and has a range of integers between 0 and 25. The original text can be transferred to encrypted text through the shift number. The major drawback of Caesar Cipher is that its range of keys is too small, making the cipher easy to break.

2.2. Simple Substitution Cipher

The Simple Substitution Cipher encrypts the plain text by shuffling the alphabet. Each letter in the alphabet has a random corresponding encrypted letter. The key to the Simple Substitution Cipher is the one-to-one relationship between the original alphabet and the shuffled alphabet.

Table 2. Example of a key of Simple Substitution Cipher.

In Figure 2, the row Ciphered Text is a randomly shuffled alphabet. Each column refers to the correspondence between each letter. Take Figure 2 as an example of the key of the Simple Substitution Cipher. When encrypting the plain text, "Believe me", B will be encrypted by F. E will be encrypted as d. L will become u. Letter i will be encrypted to letter p. V will be h. Letter m will become r. Then the cipher text of "Believe me" would be "Fdupdld rd". To decrypt, with the table above, first look at letters in row 2, Ciphered Text. Then refer to row 1, Plain Text. Each encrypted letter will be translated into the original text. For the example sentence, "Fdupdld rd", F in row 2 refers to the letter b. Letter d in row 2 points to letter e in row 1. By repeating this process, the plain text "Believe me" can be found.

Simple Substitution Cipher has a total number of 26! keys (! refer to factorial function). The first grid after the "Ciphered Text" has 26 possible letters. The second grid has 25 possible letters. The third grid has 24 possible letters. In total, to construct the whole relationship, there will be 26×25×24×…×2×1 = 26! possible keys. Compared to Caesar Cipher, this is a relatively large number of keys. It is hard for people to try every possible relationship between letters.

There is still a way to break this Simple Substitution Cipher. Same to Caesar Cipher, the post titled English Letter Frequency Counts [3] can be used to break the cipher. When receiving the complete passage, computing the frequency of each letter can help compare with the research result in the post. For instance, in the post, the letter e has a frequency of about 12.49% [3]. In the encrypted passage, the letter d also has a frequency of about 12%. Then it is reasonable to assume that the letter e can be encrypted into letter d. In the post, it is also said that the two-letter sequence, also named bigram, HE has a frequency of about 3.07% [3]. In the passage, if the two-letter sequence od also has a similar frequency 3%. Then an appropriate assumption can be made that letter h can be encrypted to letter o and letter e can be encrypted to letter d. However, this breaking solution gets a limitation as it needs plain text to be a passage. Then the frequency analysis of the passage could be accurate and helpful. It is impossible to use frequency analysis to break a Simple Substitution Cipher with only one sentence as plain text.

3. Polyalphabetic Substitution Cipher

3.1. Vigenere Cipher

Table 3. Vigenere table.

Around 1467, Leon Battista Alberti gave the first well-documented description of a polyalphabetic Cipher [4]. Later, Johannes Trithemius invented the tabula recta, which is the shifted alphabet. This invention is a critical component of the Vigenere cipher. In 1553, Giovan Battista Bellaso, the Italian cryptographer, added a key to switch between the tabula recta, making the system more secure than before. Later on, in 1586, Blaise de Vigenere, the French physicist, invented a type of polyalphabetic cipher called an autokey cipher and demonstrated it at the court of Henry III of France. In the 19th century, the invention of the Bellaso cipher was mistakenly attributed to Vigenere. This cipher was later called the Vigenere Cipher [5].

The encryption of the Vigenere Cipher needs the Vigenere Table, shown in Figure 3. Take the key, CIPHER, and text "do not take it to heart" as an example. Since the key, CIPHER, has six letters, the plain text also needs to be grouped into every six letters. Then the result can be shown in Figure 4.

Table 4. Key-plaintext relation table.

According to Figure 4, for every plain text row, find the intersection in Vigenere Table between its corresponding key letter. Plain text letters refer to the top horizontal line and the key letter refers to the left vertical column, shown in Figure 3 as bold. To encrypt the first letter, find the letter d in the Vigenere Table which is the fifth grid of the top horizontal line is also the letter d, referring to column 5, and the letter C in the Vigenere Table which is the fourth grid of left vertical column, meaning row 4. The intersection between column 5 and row 4 is f. Thus, the cipher text of the letter d by the key letter C is the letter f. Repeating the whole process can result in the sentence "fw cvx kcst px kq pthvk". [6]

To decrypt, with the sentence "fw cvx kcst px kq pthvk", separate the letter into groups and each group has 6 letters. The result is shown in Figure 5.

Table 5. Key-ciphertext relation table.

According to Figure 5, the key letter refers to the left vertical column, shown in Figure 3 as bold, and cipher text letters refer to the letters in the corresponding row of key letters. To decrypt the first column of cipher text, find the letter C in the Vigenere Table which is the fourth grid of the left vertical column, meaning row 4. Letter f appears on the fifth grid, referring to letter D. Letter c appears on the second grid, meaning letter A. Letter q is in the sixteenth grid, pointing towards letter O. Thus, the original text of the letters f, c, and q by the key letter C is the letter D, A, and O. Repeating the whole process can get the result sentence as "do not take it to heart".

The total number of keys is 26 to the power of n, in which n is the number of letters in the key. If n is quite large, like about 100, then it is extremely hard to guess and try all possibilities of keys. But it can also be broken by frequency analysis. Polyalphabetic Substitution Cipher is similar to Substitution Cipher. The difference is that Substitution Cipher follows the same principle, in which the same letter will be encrypted to the same other letter and it will not change. For example, in the Caesar Cipher with shift number 3, A will also be shifted to D. However, in Vigenere Cipher, the same letter in the plain text results in different cipher letters like letter x and letter k.

4. Transposition Cipher

4.1. Scytale

Scytale is usually used by ancient Spartans to send messages. In the Roman historian Plutarch, there is some description of how the Scytale works. Before sending out the messages, the key for Scytale is two pieces of wood that are alike. The woods are similar in length, diameter, and thickness. The sender and the receiver each get one piece of wood. The information will be written on parchment. By wrapping the parchment around the wood and leaving no vacant space between every lap, the message can be written down on the parchment with one letter per lap in each row. When the parchment is taken off, only some disarranged letters can be seen without the correct wood. The process of delivering the message only includes the parchment with no wood. When the receiver gets the parchment, winding it on the wood can make the information be shown. Figure 6 is a demonstration of how Scytale works [7].

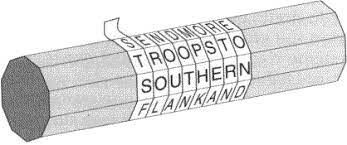
Figure 1. Scytale [8].

The key to the Scytale is wood of similar dimensions. With the wrong wood and wrong dimensions, the number of letters being shown in each column will be different. For example, in Figure 6, there are 4 letters in each column. However, with a thinner stick, there will be more than 4 letters in each column and it makes the receiver unable to read the message. The development of Scytale is the Columnar Transposition as the illustration of Scytale can be written as a rectangle [7].

4.2. Rail Fence Cipher

Rail Fence Cipher is also called Zigzag Cipher. It gets its name from its process of encryption [9]. Suppose the plain text is "I have a secret to tell you" and the key number is 3. Then the text can be written starting from the top left corner, writing three rows vertically. The result can be shown in Figure 7. The text can be encrypted as a long-length word, "Ivsrteyheeeoloaacttlu".

Table 6. Plain text after Rail Fence Cipher.

To decrypt, the text should be divided into three rows. There are 21 letters in the text. With the key number as 3, then there should be 7 letters in each row. The text can be transformed into "Ivsrtey heeeolo aacttlu". Taking every first letter in each group. Then take the second letter from each group. Repeatedly, the text "Ihaveasecrettotellyou" will be the result. Thus, the plain text "I have a secret to tell you" can be formed.

Another form of Rail Fence Cipher is in W form. Writing the letters in the W form will get the result of Figure 8. The result of the arrangement of letters will be different from the normal form. In this W form, the encrypted text is "Ietluhvaertoeloasety", which is a little bit different from the normal form.

Table 7. Plain text after Rail Fence Cipher in W form.

5. Conclusion

Classical Cryptography can be roughly divided into three categories, Substitution Cipher, Polyalphabetic Substitution Cipher, and Transposition Cipher. In this essay, each category is provided with several examples. Substitution Cipher is the substitute of one letter for another letter. It usually follows a general principle and once one pattern between 2 letters is found, it will not change. In Caesar Cipher, all plain text should be encrypted by shift number. In Simple Substitution Cipher, one letter is linked to another letter randomly. Once the encryption method is defined, the corresponding ciphertext of the same letter will not change, and only one possible corresponding ciphertext exists. Polyalphabetic Substitution Cipher is a type of transformation of Substitution Cipher. Simple Substitution Cipher uses a group of letters to be the key for encryption. The difference between Simple Substitution Cipher and Substitution Cipher is that there could be different corresponding ciphertexts for the same plain text [10]. Transposition Cipher is to shift the places of the plain text. The Difference between Transposition Cipher and Substitution Cipher is that the plain text in Substitution Cipher does not be changed to another place [10]. Instead, the plain text has been substituted by other letters. But for the Transposition Cipher, the plaintext is staying unchanged but the Cipher changes its position.

The essay concludes a way of classification of the ciphers. However, the classification is still on a preliminary model and in each group, only several examples of ciphers are included in this essay. To make a complete categorization of Classical Cipher, there is still lots of work to do including more Cipher examples and improving the whole classification system.