1. Introduction

Fractal is a newly developing subject used to study nature and irregular images and patterns, which was first stated and named by Mandelbrot [1]. He raised this concept based on his profound and massive research of natural shapes. He named it fractal from the Latin word fractus. The meaning of fractus is just as what he thought because fractal is irregular, fractional, and fractured, and fractus, in its original meaning, is a cracked and dissociated fragment. He believed that the thoughts of fractal geometry can deal with complex and strange irregular objects in nature. In the decades that followed, many mathematicians and physicians extended his theorem. Besides, fractals can be seen as a unique and brand new angle of view in the research of the calculation of complex problems [2]. They use the fractal theorem to observe some patterns in historical relics and modern design. They have also applied the fractal theorem in many aspects. These applications have profoundly affected the society and life of human beings, but people hardly feel them. These applications are based on the most significant characteristic of fractal, self-similarity. These applications have commonly affected the daily life of the public and their view of the world.

Moreover, Mandelbrot defined self-similarity as the part shape is similar to the entirety in some way [3]. For example, fractal images are specific shapes with self-similarity, which means they look the same in any magnification. Therefore, this particular shape can be divided into several parts, each of which is (at least approximately) a copy of one of the original shapes on a small scale. So, shapes with such a feature can be seen as fractal geometry, and all fractal geometry patterns own this feature. Specialists use this feature to generate many meaningful shapes and patterns.

This paper is based on the former research of fractal geometry and self-similarity; it contains four parts. Section 1 introduces the meaning and explanation of fractal geometry, and section 2 discusses some famous examples, including the Koch curve and Sierpinski triangle gasket, and leads to the definition of self-similarity. Section 3 provides some self-similar phenomena in nature and application in life, including measuring the coastline's length, the similarity of stock market quotation in specific dimensions of space and time, and the self-similarity of exploration in geometry. The goal of this passage is to give and explain the meaning of fractal geometry, discuss the explanation of self-similarity of fractal geometry and provide applications of self-similarity in real life.

2. Fractal geometry

Fractal geometry is a branch of geometry, but it is different from geometry. It is a completely brand-new angle to describe and explain the world. It can be used to provide a different method to observe some physical and chemical phenomena. It can also be used to observe the natural landscape and scenery. Scholars and specialists use its characteristics to generate some meaningful academic patterns and shapes to elucidate fractal geometry further.

However, the public seems to not realize that they are affected by fractal geometry. In fact, fractal geometry is everywhere in nature and daily life [4]. For example, the designed patterns on the floor ties are common in public life, they usually have some similar patterns to each other, which can be seen as the application of fractal geometry; the patterns on the historical relics are also similar; the rivers and mountains themselves are indeed kind of similar if people observe them in an appropriate angle. The fractal geometry provides a special view to observe this world, it can bring people a feeling to discuss its interrelationship.

Fractal geometry is significant for human beings because it can turn complex problems into simple and easy questions, which will vastly simplify the progress of calculation and tremendously lift efficiency [5]. It can use the characteristic of similarity of objects to find out their interrelationship. So fractal geometry gives people a wide angle to realize this world.

Fractal geometry patterns and shapes are usually intuitionistic, once people get to know the meaning of fractal geometry, they will easily judge whether a shape is fractal geometry or not. Even they can use the theorem of fractal geometry to design some patterns based on the most important characteristic of self-similarity.

3. Self-similarity

Self-similarity means that the part shapes are similar to the whole one in some way [6]. In common, it contains three types, exact self-similarity, approximate self-similarity, and statistical self-similarity. This passage only introduces the former two types.

3.1. Style and spacing

Exact self-similarity is strictly and precisely similar between the part and the whole shape in all scales and ranges. There are three examples below to explain this concept further.

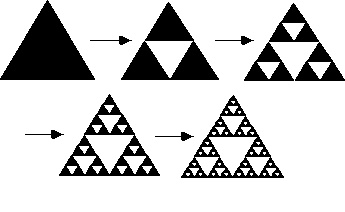
3.1.1. Sierpinski triangle gasket. This is the constitutive process of the Sierpinski triangle gasket below. This process starts first with an equilateral triangle, dividing this triangle into four same little ones and removing the middle one. Then repeat the same stages above to the rest three little triangles and continuing in this way infinitely gives rise to the Sierpinski triangle gasket [7]. In Figure 1, it can be clearly found that the small triangle is similar to the bigger one, which means the small triangle can be magnified to be a bigger one. So regardless of which triangle is chosen, it can always be seen as a triangle magnified or shrunk by others, and the parts are always strictly similar to the whole triangle.

Figure 1. The process of producing the Sierpinski triangle. (Source: https://timefliesedu.com/2019/ 03/07/sierpinskis-triangle/).

3.1.2. Koch curve. The second example is the Koch curve. The generation stages of the Koch curve are similar to the Sierpinski triangle gasket. In Figure 2, these steps start with a line, dividing this line into three equal parts and constructing an equilateral triangle based on the middle line segment. Then remove the middle line remain the rest four lines and repeat the steps on every line above infinitely to get the Koch curve [8]. It can be shown that every line is similar to others, which means the short line can be magnified to be a longer one, and the long line can be shrunk to be a smaller one. So whatever a line is chosen, it can always be seen as a line magnified or shrunk by others, and the small parts are always precisely similar to the whole curve [8].

Figure 2. Process of producing the Koch curve. (Source: https://fractalfoundation.org/resources/ fractivities/koch-curve/).

Overall, all generations of these examples are based on the same characteristic, self-similarity. Their constitutive procedure is almost the same and every part is strictly and precisely similar with the whole fractal. It also means that only using mathematical theorem and technology can generate exact self-similarity.

3.2. Approximate self-similarity

Approximate self-similarity is more sketchy and common, it is also similarity between the part and the whole shape, but not all scale and range.

Figure 3 is a composite image of magnified branches. With the continuing magnification of the branches' image, it leads to the conclusion that the part branches are similar to the whole branches. But it is unsustainable. If this picture of branches is magnified infinitely, it will finally be a wispy spot or a line segment.

So approximate self-similarity is confined by some range and scale. Some objects will no longer approximate self-similarity if their magnification exceeds some extent. However, this type is the most common self-similarity in nature, it can be easily found in real life.

Figure 3. The approximate self-similar branch of a tree [8].

3.3. Self-similar phenomenon in nature

Figure 4. The self-similar mountain and river in a high shot. (Source: https://www.108hei. com/archives/4885).

In Figure 4, these self-similar phenomena in nature are the most common approximate self-similarity. Although it can be seen as self-similar in this picture, when people observe them in an extremely big or small shot, this phenomenon will no longer exist.

3.4. Applications of self-similarity

There are many applications of self-similarity. Almost every professional field is relevant to it. It provides a new and unique angle to view this world. There are three examples below.

The coastline can not be precisely measured because the edge of the coastline is irregular, and standardized scaling tools can not measure it. If rulers are used to measure the coastline, the length of the coastline is theoretically infinite because the ruler can only measure a straight line, and the edge of the coastline is winding and continuous [9]. It means that let a spot measure a line. Therefore, the length of the coastline can not be differential. If the fractal theorem is used to deal with this problem, the coastline can be infinitely shrunk and magnified; it can be seen as using a ruler to measure a line, and the problem could be resolved.

The view of a fractal can also observe the ups and downs of the stock market. The stock market quotation is self-similar in specific dimensions of space and time because the trends are always seen as waves; they are similar, no matter how big or small [10]. So, the financial analyst can forecast the trend of the future stock market by using the characteristic of self-similarity of the market, and the economist can analyze and summarize the trend of the future world economy. People can use the self-similarity of stock market quotations and economic trends to judge whether they should save money or buy goods.

The geographer can explore terrain and landforms in this way. In Part 2, the author shows that rivers and mountains can be observed to have the characteristic of self-similarity in certain viewing angles. When geographers explore unknown topography, they can deduce the unknown from the known to judge what it is.

So, it can be clearly shown that self-similarity in fractal geometry can be seen in a circle. Whatever shape is shrunk or magnified, it can be found that this shape can always be seen as itself, which is contraction.

However, the self-similarity in fractal geometry is its shining point; specialists can use this characteristic to deal with most complex problems. Until now, scientists and mathematicians have cooperated to solve some complex physical and chemical phenomena; they can view this phenomenon differently and try to link it with self-similarity and fractal it to reach a remarkable conclusion.

Nowadays, artists have created many fantastic paintings, sculptures, and buildings. Most of these artworks have the characteristic of self-similarity; the public can appreciate one artwork more easily if they enjoy this artwork in the view of self-similarity. They can also use this angle to enjoy the landscape, such as lakes, rivers, and mountains.

An ancient book, I Ching, shows that though the historical events are different, their nature is similar; though the stages of history are separated by hundreds of years, their nature is similar. This remains essentially the same despite all apparent changes.

So, viewing this world from a unique angle, self-similarity, it would come to a minority but fitting conclusion.

4. Conclusion

The characteristic of self-similarity widely exists in nature and real life. Approximate self-similarity is most common among the natural landscape, and exact self-similarity is almost exclusively in manufactured things and shapes. Self-similarity is one of the most significant characteristics of fractal geometry. It can be regarded as fractal geometry based on self-similarity. If self-similarity is missed, fractal geometry will no longer exist. The applications of self-similarity are wide; specialists can use it to combine mathematics and natural science to research physical phenomena, and analysts can use it to forecast the trends of certain things like the stock market and economy. People can use it to enjoy the beautiful scenery and landscape more easily and appreciate the artworks and historical relics from a unique angle. It can also be used to generate regular objects. The Koch curve and Sierpinski triangle gasket are well-known examples.

Fractal geometry originates from nature, a summary of nature and life. It is a branch of geometry, but it is different from geometry. It is the thoughts combining simpleness and complexity. Applying the fractal geometry theorem in daily life would give a new and unique view of this world. With deeper study and research, it will break the narrow world cognition of the public, broaden the horizon of people, and boost the progression of science and technology.