1. Introduction

Group movement is an orderly movement that occurs spontaneously in a system composed of many self-driven units [1-3]. These phenomena are studied through experiments, simulations [4], and theory [5, 6]. One of the most famous models is the Vicsek model introduced by Tamás Vicsek et al. in 1995 [7].

In previous work, the average velocity of all particle motions was used as the order parameter of the Vicsek [7-9] model. Tamás Vicsek and others believe that the type of phase transition that occurs in the Vicsek model is a continuous phase transition. However, the continuity of the Vicsek model phase transition has been questioned by Chaté et al. [8, 9]. Chaté et al. believe that in real systems, the Vicsek model has this discontinuity characteristic. Therefore, the continuity of phase transitions in the Vicsek model is not exactly defined.

Huepe et al. [10] questioned the use of velocity as the order parameter of the Vicsek model. They discussed the number density of particles that act on particles as the order parameter of the Vicsek model, and considered that the phase transition type of the Vicsek model is continuous phase transition.

Due to disputes over the order parameters and phase transition types of the Vicsek model, continuous phase transitions and discontinuous phase transitions appear in different regions in the phase diagram of the Vicsek model drawn by R. T. Wicks et al. [11].

Xu Li et al. applied the eigen microstate method to the study of Vicsek model and found that there are three main eigen microstates [12]. Continuous phase transition and discontinuous phase transition exist at the same time. However, Li et al. [12] only discussed the impact of noise on the Vicsek model in a small noise range, and did not discuss the impact of density on the Vicsek model, and did not calculate the specific critical exponent of the Viscek model. It is difficult to describe the behavior of the Vicsek model in the entire phase space.

Based on this, this paper first further studies the Vicsek model under the influence of noise, and calculates the size of the specific critical exponent. Secondly, this paper discusses the behavior of the Vicsek model under the influence of density. Finally, through a large number of numerical simulations, the Vicsek model is drawn phase diagram, thereby illustrating the behavior within the phase space of the Vicsek model. And the entire phase space is divided into an ordered liquid phase, a disordered liquid phase, and a disordered gas phase.

2. Vicsek model and Eigen microstates

Tamás Vicsek et al introduced the Vicsek model in 1995 [7]. In the model, the particle is described as the direction of the particle position \( {r_{i}}(t) \) and particle velocity \( {Θ_{i}}(t) \) . The evolution of particles is determined by the following two equations:

\( \begin{cases}\frac{{Θ_{i}}(t)={⟨{Θ_{j}}(t-∆t)⟩_{|{r_{i}}-{r_{j}}| \lt r}}+∆θ(t)}{{r_{i}}(t+∆t)={r_{i}}(t)+{v_{0}}∆t(\begin{matrix}cos{{Θ_{i}}(t)} \\ sin{{Θ_{i}}(t)} \\ \end{matrix})}\end{cases}, \ \ \ (1) \)

where \( {〈{Θ_{j}}(t)〉_{|{r_{i}}-{r_{j}}| \lt r}} \) is the average motion direction of particles within distance \( r \) ; and \( ∆θ(t) \) is in the range of \( [-\frac{η}{2},\frac{η}{2}] \) uniform disturbance. When the particle moves, it moves in a new direction according to the given speed \( {v_{0}} \) .

At the initial moment, \( N \) particles will be evenly distributed in the periodic two-dimensional space of \( L×L \) .

For the Vicsek model, we introduce the neighbor number density of particle \( i \) at time \( t \) :

\( {n_{i}}(t)=\frac{{N_{i}}(t)}{π{r^{2}}}, \ \ \ (2) \)

where \( {N_{i}}(t) \) represents the number of neighbors to particle \( i \) at time \( t \) . From this, we can get the fluctuation of the neighbor number density of particle \( i \) at time \( t \) .

\( δ{n_{i}}(t)=\frac{{n_{i}}(t)-\bar{n}}{\bar{n}}, \ \ \ (3) \)

where \( \bar{n} \) is the average number density of neighbors of \( N \) particles at \( M \) time points:

\( \bar{n}=\frac{1}{MN}\sum _{t=1}^{M}\sum _{i=1}^{N}{n_{i}}(t).\ \ \ (4) \)

Based on this, the state of particle \( i \) at time \( t \) can be described as:

\( {s_{i}}(t)=[\begin{matrix}cos{{θ_{i}}(t)} \\ sin{{θ_{i}}(t)} \\ δ{n_{i}}(t) \\ \end{matrix}],\ \ \ (5) \)

where \( {θ_{i}}(t) \) is the movement direction angle of particle \( i \) at time \( t \) . Writing the state of \( N \) particles at time \( t \) together, and performing singular value decomposition after normalization:

\( A=\sum _{n = 1}^{r}{σ_{n}}A_{n}^{E}=\sum _{n = 1}^{r}{σ_{n}}{v_{n⨂{u_{n}}}},\ \ \ (6) \)

\( {A_{ij}}=\sum _{n = 1}^{r}{σ_{n}}{({v_{n}})_{i}}{({u_{n}})_{j}}.\ \ \ (7) \)

Furthermore, the weight \( W_{n}^{E} \) of the eigen microstate in the Vicsek model can be obtained, where \( W_{n}^{E}= σ_{n}^{2} \) . In this way, the original Vicsek model can be used as an eigen microstate \( U= [{u_{1}},{u_{2}},⋯,{u_{r}}] \) and the probability density distribution \( {w^{E}}= [w_{1}^{E},w_{2}^{E},⋯,w_{r}^{E}] \) corresponding to each eigen microstate. Then, arranging the \( {σ_{n}} \) corresponding to the eigen microstates in order from large to small. The greater the value of \( {σ_{n}} \) , the greater the value of \( W_{n}^{E} \) .

3. Expansion of scaling analysis of eigen microstate method and group motion

In this chapter, we further analyze the phase transition of the Vicsek model under different noises, calculate the critical exponent of the Vicsek model, and study the phase transition of the Vicsek model under different densities.

3.1. Phase transition of Vicsek model under different noise

The probability amplitude \( {σ_{n}} \) of the eigen microstate \( {u_{n}} \) satisfies the scaling form:

\( {σ_{n}}(η,L)={L^{-\frac{{β_{η}}}{{υ_{η}}}}}{f_{I}}({h_{η}}{L^{\frac{1}{{υ_{η}}}}}), \ \ \ (8) \)

Where \( L \) is the system scale, \( {β_{η}} \) is the critical exponent of \( {σ_{n}} \) under the influence of noise, \( {υ_{η}} \) is the critical exponent of the correlation length under the influence of noise, \( {h_{η}} \) is the distance from the noise to the phase transition point. The system weight factor satisfies the scaling form:

\( W_{n}^{E}(η,L)=σ_{n}^{2}(η,L)={L^{-2\frac{{β_{η}}}{{υ_{η}}}}}f_{I}^{2}({h_{η}}{L^{\frac{1}{{υ_{η}}}}})={L^{-2\frac{{β_{η}}}{{υ_{η}}}}}{F_{I}}({h_{η}}{L^{\frac{1}{{υ_{η}}}}}).\ \ \ (9) \)

Taking the partial derivative of \( {h_{η}} \) , then:

\( \frac{∂W_{n}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}}}{∂{h_{η}}}={L^{\frac{1}{{υ_{η}}}}}F_{I}^{ \prime }({h_{η}}{L^{\frac{1}{{υ_{η}}}}}).\ \ \ (10) \)

The partial derivative of \( W_{n}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}} \) with respect to \( {h_{η}} \) and the system scale \( L \) satisfy a power law relationship.

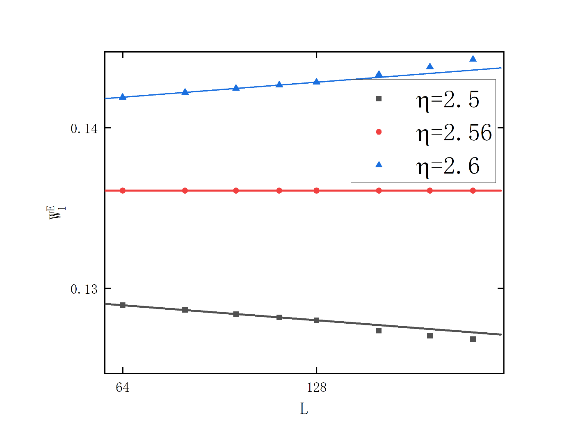
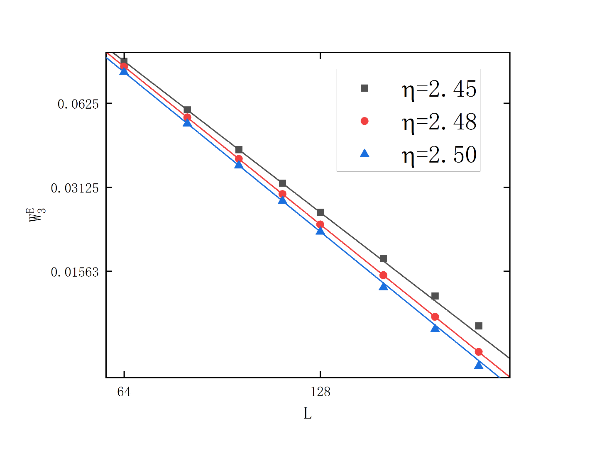
Figure 1. (Color online) \( Log-Log \) plot of \( W_{I}^{E} \) versus \( L \) around transition points: (a) \( W_{1}^{E} \) , \( {η_{1c}}=2.56 \) , \( \frac{{β_{1η}}}{{ν_{1η}}}=0 \) ; (b): \( W_{2}^{E} \) , \( {η_{2c}}=2.48 \) , \( \frac{{β_{2η}}}{{ν_{2η}}}=0.94 \) ; (c): \( W_{3}^{E} \) , \( {η_{3c}}={η_{2c}}=2.48 \) , \( \frac{{β_{3η}}}{{ν_{3η}}}=\frac{{β_{2η}}}{{ν_{2η}}}=0.94 \) ;( Li et al. [12].)

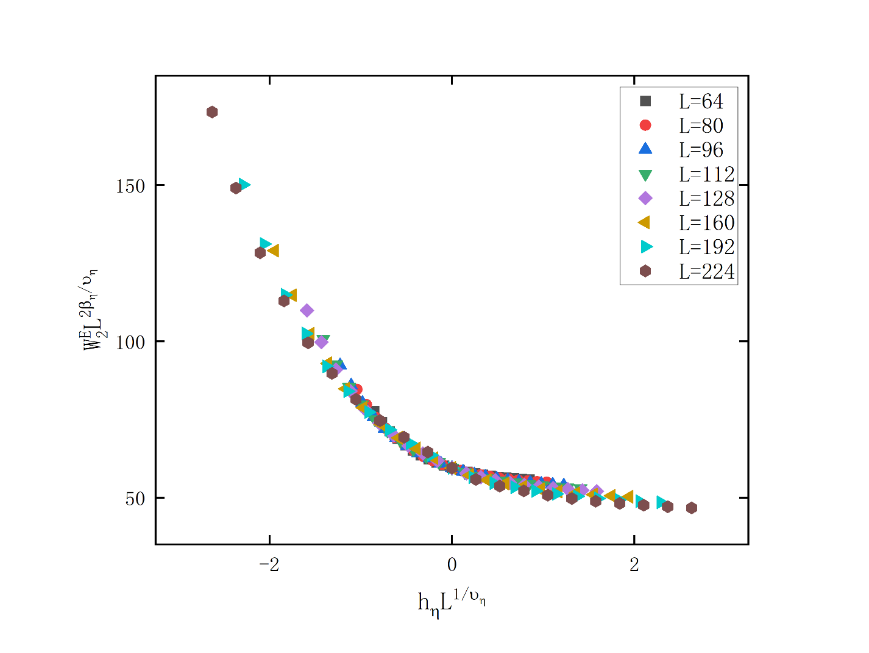
Taking the data of \( ρ=0.5 \) as an example, as shown in Figure 1, the first largest eigen microstate of the Vicsek model undergoes a discontinuous phase transition at \( {η_{1c}}=2.56 \) . As shown in Figure 1, the second largest eigen microstate of the Vicsek model undergoes a continuous phase transition at \( {η_{2c}}=2.48 \) and \( \frac{{β_{2η}}}{{ν_{2η}}}=0.94 \) . As shown in Figure 1, the second largest eigen microstate of the Vicsek model undergoes a continuous phase transition at \( {η_{3c}}={η_{2c}}=2.48 \) and \( \frac{{β_{3η}}}{{ν_{3η}}}=\frac{{β_{2η}}}{{ν_{2η}}}=0.94 \) . It is consistent with the conclusion of the work of Li et al. [12]. As shown in Figure 2, the relationship between \( W_{2}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}} \) and \( {h_{η}}{L^{\frac{1}{{υ_{η}}}}} \) is analyzed. It can be found that near the critical point, that is, within the range of \( η≈{η_{c}} \) and \( {h_{η}}{L^{\frac{1}{{υ_{η}}}}}≈0 \) , data at different scales can be scaled together. This means that within this range, the critical phase transition phenomenon of the Vicsek model still exists at different scales.

(b)

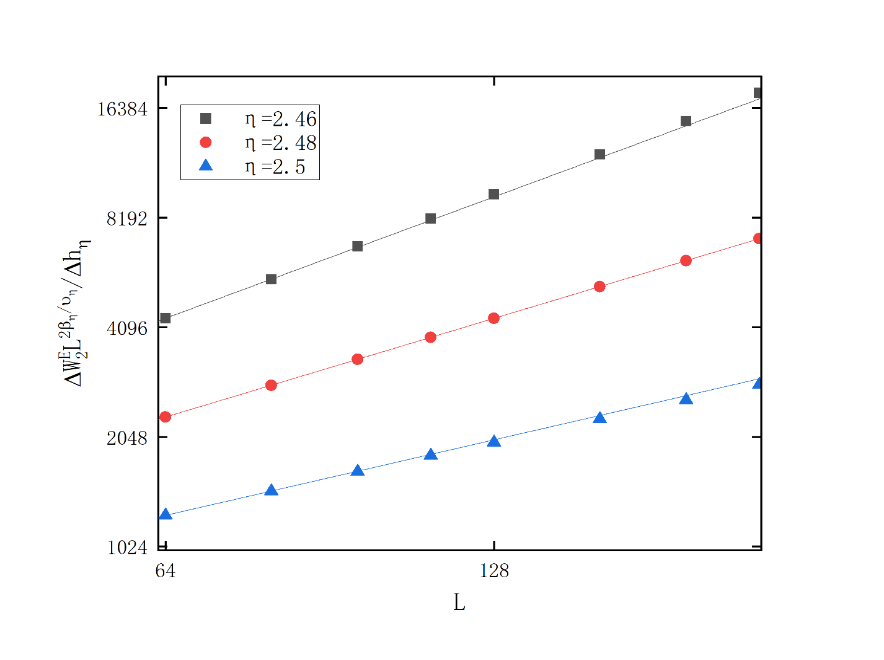
Figure 2. Log-Log plot of around transition points (a)The relationship between \( W_{2}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}} \) and \( {h_{η}}{L^{\frac{1}{{υ_{η}}}}} \) in the second largest eigen microstate at \( ρ=0.5 \) ; (b): \( Log-Log \) plot of the partial derivative of \( W_{2}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}} \) with respect to \( {h_{η}} \) : \( \frac{1}{{υ_{η}}}=1.20 \) . (Since the results in the simulation analysis are discontinuous, the difference is used instead of the partial derivative here.)

As shown in Figure 2, by calculating the partial derivative of \( W_{2}^{E}(η,L){L^{2\frac{{β_{η}}}{{υ_{η}}}}} \) with respect to \( {h_{η}} \) , and analyzing it as the system scale L changes, it can be found that a power law relationship is satisfied between them. The reciprocal of a straight line in Figure 2 whose slope is a critical exponent. The reciprocal of the critical exponent. Then the critical exponent \( {β_{η}}=0.783 \) of the probability amplitude \( {σ_{n}} \) under the influence of noise and \( {ν_{η}}=0.833 \) of the correlation length under the influence of noise can be ontained.

4. Conclusion

This paper explores the scaling form and weight factor critical exponent of the continuous phase transition by an in-depth study of the microstate characteristics of the Vicsek model under different noise and density conditions, using the finite scale scaling method. The authors highlight the influence of density on the Vicsek model, revealing the phase transition behavior that emerges in different eigen microstates. By comparing the behavior under different parameter conditions, it can be found that noise play a key role in the Vicsek model.