1. Introduction

In the realm of information security, the CIA triad (Confidentiality, Integrity, and Availability) represents three pivotal facets to heed [1]. Standing as a foundational element of information security, cryptography predominantly centers on data integrity and confidentiality. It utilizes mathematical algorithms to morph data into an unintelligible and scrambled form during storage and transmission, barring unauthorized access to the safeguarded data. Pinpointing the exact inception of cryptography proves challenging, with its comprehensive development emerging prominently during the Renaissance. Initially, cryptography was a basic practice of substituting letters with others in a distinctive sequence. The significant leap in cryptography occurred in 1977 with the U.S. government’s release of the Data Encryption Standard (DES) [2], signaling a transformative progression in the field. The year 2001 saw the unveiling of the Advanced Encryption Standard by the American National Institute of Standards and Technology. Despite both DES and AES falling under the umbrella of symmetric cryptography, this article delves deeply into AES. Conversely, the RSA algorithm, emerging in 1978, is an exemplar of asymmetric cryptography. Named after its innovators (Rivest, Shamir, and Adleman), RSA distinguishes itself by employing separate keys for encryption and decryption, with only the encryption key available publicly [3]. This contrasts with the symmetric cryptography approach where a singular secret key is utilized for both encryption and decryption processes.

2. Relevant theories

2.1. Euler’s Totient Function

The Euler's totient function, also called totient function, is denoted as \( φ(n) \) . It counts the number of positive integers less than or equal to n that are relatively prime to n, or the number of totatives of n.

The equation of Euler’s totient function is defined as follows:

\( φ(n)=\prod _{(p|n)}(1-\frac{1}{p})\ \ \ (1) \)

For example, \( φ(80) \) can be obtained through the following equation:

\( φ(80)=80*{(1-\frac{1}{2})^{4}}*(1-\frac{1}{5})\ \ \ (2) \)

2.2. Euler’s theorem and Fermat little theorem

When positive integers a is relatively prime to n, there is the following formula:

\( {a^{φ(n)}} ≡ 1(mod n)\ \ \ (3) \)

Fermat little theorem is a special condition derived from Euler’s theorem (when n is a prime number):

\( {a^{p-1}} ≡ 1(mod p)\ \ \ (4) \)

In this formula, p-1 = \( φ(p) \) . This is because p is a prime number, the only prime factor of n is n itself. Then, \( φ(p) \) is given by this formula: \( φ(p) \) = \( p*(1-\frac{1}{p}) \) =p-1

2.3. Chinese Remainder theorem

Chinese Remainder theorem is defined as:

When m₁, m₂, ..., mₙ are pairwise coprime positive integers, and a₁, a₂, ..., aₙ are integers, Then the following equation must have solution:

\( \begin{cases} \begin{array}{c} x≡{a_{1}}(mod {m_{1}}) \\ x≡{a_{2}}(mod {m_{2}}) \\ …… \\ x≡{a_{n}}(mod {m_{n}}) \end{array} \end{cases}\ \ \ (5) \)

The solution x can be obtained by the equation (N is the product of all \( {m_{i}} \) :

\( x≡\sum _{i=1}^{n}{a_{i}}×\frac{N}{{m_{i}}}×[{(\frac{N}{mi})^{-1}}]\ \ \ (6) \)

3. RSA and AES cryptography

3.1. Introduction to AES

The Advanced Encryption Standard, initially termed the Rijndael algorithm [4], is the brainchild of Belgian cryptographers Joan Daemen and Vincent Rijmen. Presented alongside twenty other algorithms to the National Institute of Standards and Technology (NIST), the Rijndael algorithm was ultimately published as the AES algorithm by NIST on November 26, 2001. Serving as a robust alternative to the Data Encryption Standard (DES), AES operates as a block cipher encryption algorithm, utilizing a symmetric key for both the encryption and decryption of data [5]. AES processes a plain-text of 128 bits, while accommodating encryption and decryption keys of 128 bits, 192 bits, and 256 bits. An additional two rounds are necessitated for every incremental 64 bits in the key. Within this framework, both text and key undergo a conversion into a 4*4 matrix, with each byte represented as a hexadecimal number. This discussion centers primarily on the utilization of a 128 bits key in AES. Figure 1 outlines the fundamental encryption process for a 128 bits key within AES. For decryption, this process is executed in reverse. The procedure unfolds across three primary sections: Key Expansion. Nine Rounds Circulation:

a. Byte Substitution.

b. Row Shifting.

c. Column Mixing.

d. Round Key Addition.

Final Round:

a. Byte Substitution.

b. Row Shifting.

d. Round Key Addition.

Each section plays a crucial role, ensuring the integrity and security of the encryption and decryption processes within the AES algorithm..

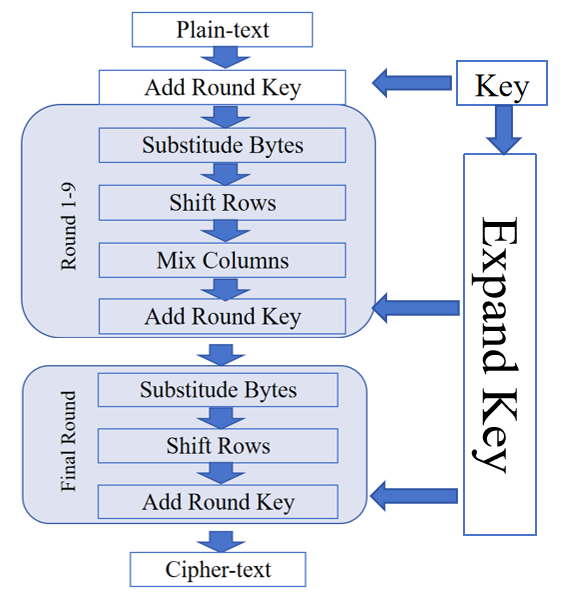
Figure 1. Process of encryption in AES (Photo/Picture credit: Original).

3.1.1. Specific process of AES. Key expansion in nine rounds and the final round, “Add Round Key” requires the original key to be expanded to generate ten round keys. As shown in Table 1.

Table 1. Original key and blank round key.

As shown in Table1., the 128 bits key is segmented into 16 sections, each section is denoted by hexadecimal number. Each column is denoted as \( {W_{i}} \) , and the columns of ten round keys are generated by the initial four column. When i is not a multiple of four, \( {W_{i}} \) = \( {W_{i-4}}⊕T({W_{i-1}}) \) ( \( ⊕ \) is a type of logical operation, called xor, such that if the values of a and b are not the same, the result is 1; If the values of a and b are the same, the result is 0). When i is a multiple of four, \( {W_{i}} \) = \( {W_{i-4}}⊕T({W_{i-1}}) \) . Function T consist of three parts:

Rotation: Shifting each section by one byte, showing in Figure 2

Substitution: Using the S-BOX to substitude the result of Rotation.

Xor-ing: Performing a xor between the result from substitution and round constant [6].

Figure 2. Rotation process (Photo/Picture credit: Original).

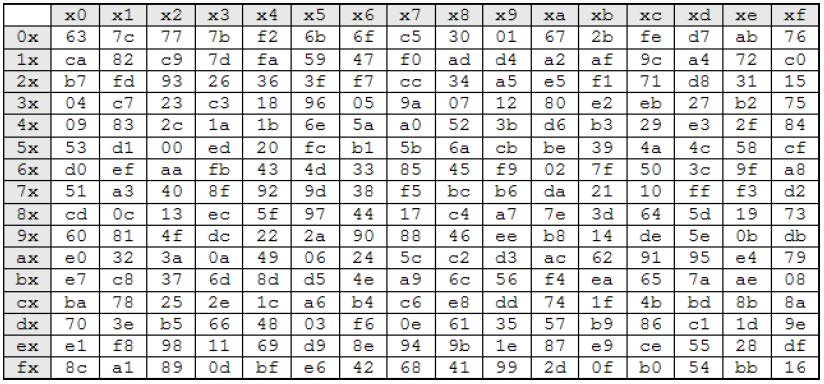
Figure 3. AES S-BOX (Photo/Picture credit: Original).

Process within nine rounds circulation and final round.

Substitude Bytes.

In this process, each byte in the matrix is substituded using the s-box.

Shift Rows:

Each row of the matrix is shifted to the left. As showing in Figure 3, the first row shifted by zero byte; for each row that follows, one more byte is shifted.

Mix Column:

The resulting matrix of “shift rows” is mixed with a given matrix using a specified formula.

Add Round Key:

Performing a xor operation between the result from “mix column” and the round key. The first “Add Round key” that was done to plain-text in Figure 4 uses the original key to do xor operation.

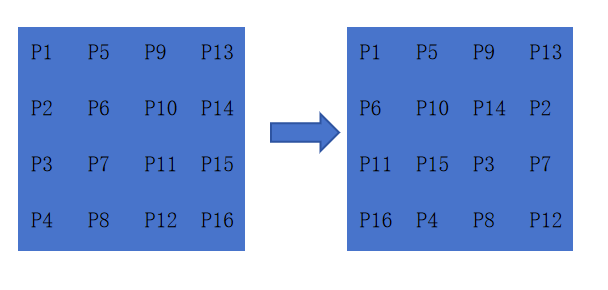
Figure 4. Process of shift rows (Photo/Picture credit: Original).

3.2. Introduction to RSA cryptography:

Using the Euler's theorem and building on Diffie and Hellman’s idea, Rivest, Shamir, and Adleman designed RSA by 1978. It uses a public-key cryptosystem and digital signatures [7]. The term public-key cryptosystem refers to a cryptosystem with a public encryption key and a secret decryption key. Every sender can use the encryption key to transform the plain-text into the cipher-text and send it to the receiver. The mechanism of public key cryptosystem is denoted by the following formula:

\( D(E(M))=M\ \ \ (7) \)

It is extremely hard to compute the decryption key D from the encryption key E without additional information, so a public E does not undermine the confidentiality of D. It is a “trap-door one-way function”, meaning that D can only be computed in one direction [8].

3.2.1. Mathematical mechanism of RSA. When Bob want to compute the private key and public key used in RSA. He first need to generate two large prime numbers p and q, let n=p*q, and find the \( φ \) (n). Because p and q are both prime numbers, \( φ \) (n) = (p - l) (q - 1). Then he find an integer b such that e is between 3 and n and relatively prime to \( φ \) (n) and a multiplicative inverse modulo d of e such that ed \( ≡ 1(mod φn) \) . n and e are public, and d is kept secret.

When Alice wants to encrypt a plain text message, the plain text is converted into a integer, call it x. Then, x is segment such that each \( {x_{i}} \) is less than n. Alice can encipher x by the following formula:

\( {y_{i}} \) ≡ \( {{x_{i}}^{e}} \) (mod n). Alice then sends the cipher text y to Bob. To decipher the cipher text y, Bob can use the following formula:

\( {x_{i}}≡{{y_{i}}^{d}}(mod n)\ \ \ (8) \)

The decryption and encryption process can be done in such way is largely because the process of generating the public and secret key. From the encryption and decryption process, \( {{y_{i}}^{d}} \) ≡ \( {{x_{i}}^{ed}} \) (mod n) can be obtained. Since ed \( ≡ 1(mod φ(n)) \) , \( {{y_{i}}^{d}} \) ≡ \( {{x_{i}}^{ed}} \) (mod n) can be written as \( {{y_{i}}^{d}} \) ≡ \( {{x_{i}}^{k φ(n)+1}} \) (mod n). Since n is the product of two large number, \( {x_{i}} \) is always relatively prime to n except x is equal to p or q. According to Euler’s theorem, \( {{x_{i}}^{k φ(n)+1}} \) ≡ \( {x_{i}} \) (mod n). A entire formula is obtained:

\( {{y_{i}}^{d}}≡{{x_{i}}^{ed}}≡{{x_{i}}^{k φ(n)+1}}≡{x_{i}}(mod n)\ \ \ (9) \)

3.2.2. Digital signature. RSA implements digital signature to ensure that senders can verify the message from the third party. If Bob, the person who has the secret key, wants to send a message to Alice, he can use the secret key d to sign the message m: s= \( {sig_{sk}}{(m)=m^{d}} \) (mod n)

Then, Bob sand the message m with the digital signature s to Alice. Alice can verify the signature using her public key e to get m’: m’= \( {s^{e}} \) (mod n). then compare m’ with m. If they are the same, then the message is from Bob since only Bob has the secret key.

3.2.3. Efficient method for decryption process. When using secret key d to decrypt the cipher text \( {y_{i}} \) , Chinese remainder theorem can be implemented to accelerate the process since owner of the secret key knows p and q. \( { x_{i}} \) ≡ \( {{y_{i}}^{d}} \) (mod n) can be rewrite as:

\( \begin{cases} \begin{array}{c} {x_{i}}≡{{y_{i}}^{d}}(mod q) \\ {x_{i}}≡{{y_{i}}^{d}}(mod q) \end{array} \end{cases}\ \ \ (10) \)

For example, when Bob gets a cipher-text 178. The secret key d is 63, and p and q are 23 and 17 (In real situation, p and q are much larger, and that is why Chinese Remainder Theorem is used). The plain-text \( {x_{i}} \) satisfies the following equation: \( {x_{i}} \) ≡ \( {178^{63}} \) (mod 391)

Applying Chinese Remainder Theorem, the equation can be rewrite as:

\( \begin{cases} \begin{array}{c} {x_{i}}≡{178^{63}}(mod 23) \\ {x_{i}}≡{178^{63}}(mod 17) \end{array} \end{cases}\ \ \ (11) \)

After the simplification using basic property of congruence and Euler’s Theorem, equation can be rewrite as:

\( \begin{cases} \begin{array}{c} {x_{i}}≡{17^{19}}(mod 23) \\ {x_{i}}≡{8^{15}}(mod 17) \end{array} \end{cases}\ \ \ (12) \)

Then, using Chinese Remainder Theorem, \( {x_{i}} \) is obtained by the following formula:

\( {x_{i}}≡17×17×{17^{-1}}(mod 23)+8×23×{23^{-1}}(mod 17)≡25\ \ \ (13) \)

3.3. Combined application of AES and RSA

Both AES and RSA have their advantages and disadvantages. With the help of the computer, AES can quickly encrypt large amounts of information. However, since AES is a symmetric key encryption, it is not secure as RSA. When p and q are large enough, RSA is almost impossible to attack, but the process of encryption and decryption can be time consuming. These limitations have made them hard to implement in some field. A combined application of AES and RSA may solve the problems to some extent.

3.3.1. A hybrid algorithm used in file encryption. File encryption requires an efficient, secure algorithm, so neither AES nor RSA can meet the requirement. A hybrid algorithm is proposed. Basically, the file is been encrypt for two times [9]. Firstly, AES is used to encrypt the file and generate first cipher-text C1. Then, the public key of RSA is used to encrypt the key of AES and C1 to get second cipher-text C2. During the decryption, the secret key of RSA is used to get C1 and the key of AES. Then, the key of AES is used to decrypt C1 to get the original file. Proposed in [10], this hybrid algorithm can secure the information even if an unauthorized third party knows the key of AES since only the secret key of RSA can decrypt C2. Also, this hybrid algorithm is more efficient than simply implement RSA. This is because AES divided text into many 128 bits sections, and each section is encrypted using RSA separately. A relative shorter section can enhance the efficiency of RSA.

3.3.2. A hybrid algorithm used in E-mail encryption. Symmetric encryption is widely used in E-mail encryption when sending sensitive and private information. However, the process of distributing the key can be risky. Also, since symmetric encryption does not have a digital signature, the identity of the information cannot be confirmed. A hybrid encryption using AES and RSA is proposed to solve such problem. As shown in Figure 5, two pairs of RSA key are generated, one pair is used to encrypted the AES key and plain-text, and another is used to sign the messages. This hybrid encryption implemented a digital signature to enable Bob and Alice to verify the identity of each other. Also, a leakage of RSA public key will not cause any risk since the secret key is not unknown for everyone except the designer of RSA key pair.

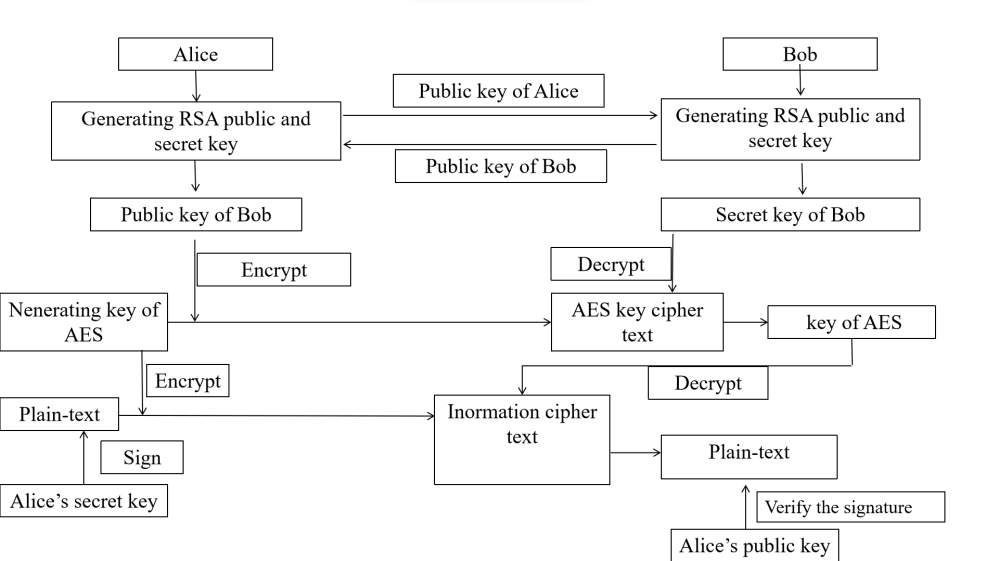
Figure 5. Process of Hybrid Encryption and Decryption (Photo/Picture credit: Original).

3.3.3. A Conclusion About hybrid algorithm using AES and RSA Algorithm. A hybrid encryption Using RSA and AES always uses AES to encrypt the data since AES is more efficient at encrypting large amount of data (it may also accelerate RSA algorithm since the text is divided into 128 bits sections). RSA is used to sign the message and to encrypt the key of AES. So, hybrid encryption avoids the process of distributing the key of AES and enables different parties to check the identity of each other.

4. Conclusion

The above discussion comprehensively explores the intricacies of encryption and decryption processes, emphasizing the utilization of formulas and theorems to enhance these operations. The text methodically explains the RSA digital signature mechanism and its crucial role in ensuring secure communication between entities. Additionally, it outlines the application of the Chinese Remainder theorem in decryption, augmenting the efficiency of the process.

Moreover, the discussion broadens to include the amalgamation of AES and RSA in a hybrid encryption algorithm. This dual application optimizes the encryption and decryption processes by harnessing the strengths of both algorithms, guaranteeing not only efficiency but also heightened security. Clear examples of hybrid encryption use cases in both file and email encryption provide a pragmatic understanding of its real-world application. In conclusion, this exploration offers profound insight into the realm of encryption, detailing processes, algorithms, and their diverse applications. It lays a robust foundation for comprehending the practical implementations and benefits of hybrid encryption mechanisms, especially the combined use of AES and RSA. The detailed exposition of processes and methodologies highlights the significance of employing stalwart encryption methods to safeguard communication and data, reinforcing the imperative for continued advancements in this essential technological field.