1. Introduction

The Twin Paradox is proposed in 1911, as a classic paradox of special relativity, in that era, the scientist applied ways like Minkowski geometry to explain and get the conclusion that there’s actually no paradox, and the time of the moving object does move more slowly. As science developed, this paradox can also be explained using general relativity’s time dilation effect in the gravitational field. Subsequently, this paradox was tested in 1971 with an experiment by American scientists [1].

As one of the greatest accomplishment in 20th century, the relativity, both special and relativity can be applied both theoretically and pragmatically in many fields that need accurate measurement as a better estimation of statics such as the satellite and the particle accelerator. The relativity has become a rudimentary theory for many advanced fields.

This paper mainly explains the Twin Paradox in the following three ways: the Lorentz transformation, the Minkowski geometry, a special geometry including both space and time, which is proposed to have a better explanation of the special relativity and gravitational time dilation in general relativity, and will also expand to other effects in relativity, such as the gravitational redshift. Through reviewing several explanations, this paper hopes to offer some references for a better understanding of the Twin Paradox.

2. Basic introduction to Twin Paradox

2.1. Contents

The Twin Paradox was proposed by French physicist P. Langevin in 1911 to question the special relativity of Einstein. This paradox introduces a case when a pair of twins went out for space travel, since the one on the spacecraft is moving relative to the one on the earth, according to special relativity, his clock will move more slowly relative to the one on the earth; however, since the earth is also moving relative to the spacecraft, the clock on the spacecraft should also move more slowly relative to the one on the earth.

According to special relativity and Lorentz transformation, time is relative in a certain reference frame with the formula

\( {t^{ \prime }}=\frac{t-\frac{vx}{{c^{2}}}}{\sqrt[]{1-\frac{{v^{2}}}{{c^{2}}}}}\ \ \ (1) \)

As for an object moving at a speed close to the speed of light, its time will be slower than a motionless one. Supposing that the speed of the spacecraft is 0.8c, as a result, the time of the earth relative to the spacecraft is \( t×\sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}} \) , which is 0.6t. However, relative to the spacecraft, the earth is also moving at a speed of 0.8t, which the formula can be uesed again to get that the time of the spacecraft is

\( 0.6t×\sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}}\ \ \ (2) \)

which is 0.36t. And that is the paradox.

2.2. Flaw analysis

This paradox might seem reasonable, but it ignores a significant period of the spacecraft-the turning back period which it needs to decelerate and then accelerate. Actually, the time the spacecraft experienced is the same as the earth has observed, which is 0.8 times of the earth. Although the earth is also experiencing this period relative to the spacecraft, the spacecraft can actually feel the overload caused by the acceleration. Specifically, the person on the spacecraft will suddenly discover that the person on the earth turns much older when he turns around. This period might seem ordinary, but it the key to this paradox. In the following passage, this paper will give three main explanation based on the acceleration.

3. Explanations of the Twin Paradox

This section mainly explains the Twin Paradox from the following three perspectives: the Lorentz transformation, the Minkowski geometry, and a special geometry.

3.1. Lorentz Transformation

In special relativity, if a motion wants to be determined, the observer must be fixed on a certain reference frame [2]. As this paper mentioned before, from the earth’s point of view, the time of the spacecraft is the same as it has experienced, because the observer on the earth remained in one reference frame. However, in the view of the spacecraft, the reference frame has changed when it turns back. That is, this motion has been separated into two parts-leaving parts and returning parts. Therefore, after getting clear of the reference frame, the calculation can be made from a fixed reference of the frame, which is the period that the spacecraft hasn’t turned back. In that reference frame, the time of the spacecraft (let \( t \) to be the total time the earth has experienced) is the same as the paradox,

\( {t^{ \prime }}=0.5×t×\sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}}×\sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}}=0.18t\ \ \ (3) \)

Where the time on the earth the observer see is \( \sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}} \) times of the time on the spacecraft, which the observer on the earth seen as \( \sqrt[]{1-\frac{{0.8c^{2}}}{{c^{2}}}} \) times of the time of the earth. However, when the spacecraft turns back, the reference frame has changed, but if a correct answer wants to be concluded, the observer must stay at the same reference frame, and according to the Lorentz Transformation of speed ( \( u \) is the relative speed between two reference frames),

\( {v^{ \prime }}=\frac{v-u}{1-\frac{vu}{{c^{2}}}}\ \ \ (4) \)

the speed of the spacecraft when it’s returning relative to the speed of it when it’s leaving is

\( {v^{ \prime }}=\frac{0.8c-(-0.8c)}{1-\frac{0.8c×(-0.8c)}{{c^{2}}}}≈0.97561c\ \ \ (5) \)

Therefore, from the reference frame of the spacecraft when it’s leaving the earth, the earth is leaving him at a speed of 0.8c, and the spacecraft is chasing the earth at a speed of 0.97561c. And the time they have experienced before they met is

\( {t^{ \prime \prime }}=t×\frac{0.5}{0.97651-0.8}≈2.8327t\ \ \ (6) \)

Therefore, from the perspective of the leaving spacecraft, the total time that the spacecraft has experienced should be the sum of the time of the spacecraft from both reference frames. Since t’’ is the time that the leaving reference observes, if the time of the returning spacecraft wanted to be gotten, Lorentz Transformation is needed to apply on it, which is:

\( {t^{ \prime \prime \prime }}={t^{ \prime \prime }}×\sqrt[]{1-{\frac{(0.97651c)}{{c^{2}}}^{2}}}≈0.62t\ \ \ (7) \)

Therefore, the total time of the spacecraft \( { t_{s}} \) = \( t \prime \) + \( t \prime \prime =0.8t \) , the exact same result as the earth observes. Conclusively, this problem is solved perfectly just using special relativity and Lorentz Transformation.

3.2. Minkowski geometry

3.2.1. Basic introduction of Minkowski geometry. Minkowski geometry is a new type of geometry that despite the basic three dimensions, it includes another dimension-time dimension which can be defined as an imaginary axis- \( cti \) . The reason for using cti as an axis owing to two reasons: the characteristic of the imaginary number (an imaginary number times i can be represented as rotating 90 degrees) matches the rotating axis of Lorentz transformation well [3], and the units of the time axis and space axis have to be the same. And because of the specialty of the imaginary numbers, the distance between two points in Minkowski geometry is different from the conventional reference frame, which its distance \( l=\sqrt[]{{x^{2}}+{y^{2}}+{z^{2}}} \) .

The world line in Minkowski geometry is \( {dL^{2}}={c^{2}}d{t^{2}}-d{l^{2}} \) [4], where \( L \) represents the distance between the points, and τ, which is L divided by c, is the world line, the time of one particular frame. Through this method, Lorentz Transformation can be explained in geometric ways in Figure 1:

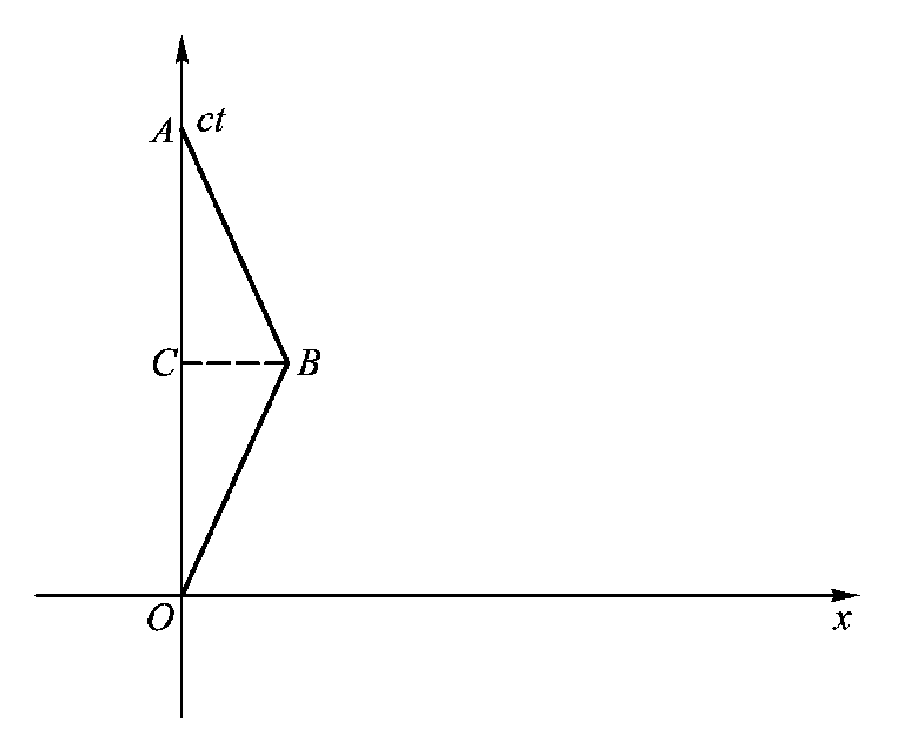
Figure 1. The graph of the Twin Paradox [4]

In Figure 1, the world line of a constant object is \( \int _{0}^{t}\frac{\sqrt[]{{c^{2}}d{t^{2}}-d{x^{2}}}}{c} \) , while x equals to zero since it doesn’t move. However, a moving object (presumed that its speed is constant) moving at a speed v’s world line is \( \int _{0}^{t}\frac{\sqrt[]{{c^{2}}d{t^{2}}-d{x^{2}}}}{c} \) . Since \( x=vt \) , now the world line of the moving object is \( t\sqrt[]{1-\frac{{v^{2}}}{{c^{2}}}} \) , which fit the Lorentz transformation exactly well.

The analysis above shows that from the one who is stable, Lorentz transformation can be applied. However, relative to the one who is moving, since moving is relative, Lorentz transformation can also be applied. The only difference is that the axis have to be perpendicular or parallel to the trail of the moving object in the frame.

3.2.2. Using Minkowski Geometry to solve the Twin Paradox. Using above conclusions, the graph of the Twin Paradox can be shown in Figure 1, where ABO represents the space-time distance of the spacecraft, and ACO is the one of the earth, and their time passed is the length of their world line.

According to this graph in Figure 1, ABO equals two times of OB, where the relationship of OB and OC has been proved before, and fits exactly well with the Lorentz transformation.

It’s also possible to use another way to explain the Twin Paradox by applying the change of the reference frame. Owing to the specialty of the Minkowski geometry, OB is actually smaller than OC, on the contrary OB=OB’, like what’s shown in the graph. Similarly, the length of AB is actually equal to AB’. And it’s obvious to see that at the time the spacecraft turns around, the world line of the earth suddenly skips from B to B’, meaning that the age of the earth surged.

3.3. General Relativity

3.3.1. Equivalence Principle. In the following section this paper states that at the instant the spacecraft turns around, which needs massive acceleration, the clock on it has been greatly slow down. Therefore, it’s suspected that acceleration will cause a time dilation which can be explained using general relativity. General relativity considered a uniform gravitational field and a uniform acceleration as equivalent. Therefore, supposing there are two apparatus that can count time, emit light signals and receive them in an elevator speeding up at a constant acceleration a. One of them is placed at the bottom of the elevator and emits two light signals with interval \( {t_{1}} \) , and the other receives them and counts the time interval \( {t_{2}} \) . Suppose that the elevator starts from the ground and let the height of the ground be zero, the motion equation of the apparatus of the ground is

\( {x_{1}}(t)=\frac{1}{2}a{t^{2}}\ \ \ (8) \)

And the one on the top of the elevator is

\( {x_{2}}(t)=\frac{1}{2}a{t^{2}}+h\ \ \ (9) \)

Where t represents the time after the elevator starting to move, and h represents the height of the elevator.

Now, presuming that the elevator starts moving and simultaneously the apparatus on the bottom emit the first the light signal, and after a time interval \( {t_{1}} \) , it emits another signal. According to these descriptions, two equations can be derived:

\( \frac{1}{2}a{t^{2}}+h=\frac{1}{2}a{t^{2}}+ct\ \ \ (10) \)

\( \frac{1}{2}a{(t+{t_{2}})^{2}}+h=c(t+{t_{1}}-{t_{2}})+\frac{1}{2}a{(t+{t_{1}})^{2}}\ \ \ (11) \)

After some mathematical derivations, it will be surprising to discover that \( {t_{1}} \) and \( {t_{2}} \) are not the same, but have a surprising relationship that

\( {t_{1}}={t_{2}}(1-\frac{gh}{{c^{2}}})\ \ \ (12) \)

According to the above calculation, if there is an observer who is at the top of the elevator, he will discover that his clock is different from the one who is at the bottom, since the interval of both signals reaching here will also decrease, which means, the time interval of the transport of the message of the start of a single second and the end of this second will also increase, which means a dilation in time. Additionally, according to the equivalence effect [5], one cannot determine whether they are at a uniform gravitational field or accelerating. Hence, the clock in a gravitational field will also become slower.

3.3.2. Gravitational Redshift. According to that conclusion, there is also another interesting phenomenon called gravitational redshift, which means the color will turn red in a gravitational field. As for an observer apart from the gravitational field, the frequency of the light in the will decrease, and since the frequency of the light impacts the color of the object, and the red light tends to have a lower frequency, the color in a gravitational field will become red relative to one who is not in the gravitational field.

3.3.3. Expain the Twin Paradox with general relativity. In this case, when the spacecraft turns around, the massive acceleration can be also considered as a strong gravitational field, in which the spacecraft’s clock will slow down [6]. Hence, when the spacecraft get rid of the gravitational field, its time has been slower than the one on the earth, which is similar to the conclusion that the Minkowski Geometry showed. There’s another explanation, since the spacecraft want to get out of the gravitational field, it has to consume energy, and since \( E=hγ \) , the frequency of the clock will also decrease, which causes a time dilation.

4. Conclusion

The Twins Paradox, proposed in 1911, is a classic paradox of the special relativity, in that era, the scientist has applied ways like Minkowski geometry to explain and conclude that there’s actually no paradox, and the time of the moving object does move more slowly. As the science developed, this paradox can also be explained using general relativity’s time dilation effect in the gravitational field. Subsequently, this paradox is been tested in 1971 using an experiment by American scientists. The twin paradox, is not in essence a paradox, but an absolute effect, it has been solved. This paper reviews the Twin Paradox and its basic explanations from three perspectives: Lorentz Transformation, Minkowski Geometry, and gravitational time dilation in general relativity. The method of discussing the twin paradox through Lorentz transformation makes full use of special relativity and is highly evaluated by the theorists. Through Minkowski Geometry, not only can the calculation be simplified, but also the whole physical situation be more clear and intuitive. This paper also introduces related theories based on the above conclusions like gravitational redshift. However, this paper is lack of some mathematical steps to prove these conclusions. Therefore, some of the supplements are still needed to be added.