1. Introduction

Quantum entanglement is a nonclassical correlation property in quantum mechanics, referring to the nonclassical relationships between multiple subsystems in a quantum system. Entangled quantum systems cannot be described as simple superpositions of individual subsystems but require consideration of the correlations between all subsystems. Even when the subsystems are far apart, a measurement on one subsystem instantaneously affects the state of other subsystems (see Figure 1). Quantum entanglement breaks the local realism of classical physics and exhibits strong nonlocal quantum correlations. This nonclassical correlation endows entangled systems with potential advantages in quantum information processing. The entanglement between two particles is the simplest form of quantum entanglement, but it is also possible to generate complex entangled states among multiple particles or entanglement between different degrees of freedom. Quantum entanglement can be classified into zero-coupling states, Bell states, W states, etc., each with its specific correlation properties. Generating and manipulating different quantum entangled states are crucial for quantum information processing [1].

Figure 1. Illustration of quantum entanglement, where the spin of one particle can affect the spin of another particle.

Quantum entanglement is an extremely weak quantum interaction, even weaker than general quantum interactions, making it difficult to detect in experiments. However, it is one of the most important concepts in quantum physics. The study of quantum entanglement can help us better understand the nature of quantum physics. It can play a significant role in fields such as quantum computing and quantum communication and can be used to achieve advanced quantum technologies, such as quantum teleportation. Quantum entanglement reveals the essence of the quantum world and serves as the foundation for the implementation of quantum communication, computing, and other technologies, making it of great significance in quantum information science.

In conclusion, quantum entanglement is an important phenomenon in quantum physics that can help us better understand the field and enable advanced quantum technologies such as quantum computers and quantum communication. This paper focuses on the phenomenon and principles of quantum entanglement, reviews the scientific principles and related applications of quantum entanglement, and discusses current challenges and future directions in its development.

2. Theoretical Foundations of Quantum Entanglement

This section provides a detailed exposition of the theoretical foundations of quantum entanglement. The aim is to comprehensively and systematically equip readers with the understanding of the characteristics, classification methods, measurement tools, operational techniques, and dynamical evolution laws of quantum entanglement, thus laying the groundwork for subsequent applications.

2.1. Characteristics of Quantum Entanglement

Quantum superposition refers to the ability of a quantum system to exist in a superposition state of different quantum states. In quantum physics, a quantum state describes the state of an isolated system and contains all the information about the system. According to Born’s statistical interpretation of wave functions, knowing the information about the quantum state of a system allows us to determine the results of measurements on the system. Quantum states can be classified as pure states or mixed states. A superposition state, also known as a superposition state, is a state obtained by a linear combination of several quantum states of a quantum system that are normalized [2]. The states of an electron with coherent spin to the right and a positron with coherent spin to the left are correlated, which is referred to as quantum coherence. This coherence can only be explained by quantum theory, or the “correlation between states.” One explanation is based on a hypothetical experiment proposed by Einstein and his collaborators in 1935. In this thought experiment, an electron and a positron, generated by energy in a high-energy accelerator, fly in opposite directions. When not observed, both particles exist in a superposition state of spin to the right and spin to the left. However, when measured and the electron is observed in the spin to the right state, the positron must be in the spin to the left state due to the conservation law, as the electron and positron are created from energy conversion. This correlation between the states of “electron spin to the right” and “positron spin to the left” is known as “quantum coherence” [3]. Quantum coherence is essential for achieving efficient parallel computations in quantum computers. Quantum bits (qubits) that are related to each other act as a collective entity. Therefore, any manipulation of one qubit immediately affects the other qubits in the sequence. This characteristic is the key to the high-speed computation capability of quantum computers [4].

Figure 2. Schematic of Quantum Entanglement Properties[5]

2.2. Classification of Quantum Entangled States

Quantum entanglement can be classified into three types based on the relationship between quantum systems: pure state entanglement, mixed state entanglement, and composite state entanglement.

1. Pure State Entanglement: When two or more quantum systems are in a pure state, their entanglement is referred to as pure state entanglement. In pure state entanglement, the states of two or more systems are completely correlated, resulting in strong interactions between them. For example, the state changes of entangled particles in pure state entanglement are completely identical.

2. Mixed State Entanglement: When two or more quantum systems are in a mixed state, their entanglement is referred to as mixed state entanglement. In mixed state entanglement, the interactions between two or more systems are partially correlated. Therefore, this type of entanglement is weaker than pure state entanglement. For example, the state changes of entangled particles in mixed state entanglement are partially identical.

3. Composite State Entanglement: When two or more quantum systems are in different states, their entanglement is referred to as composite state entanglement. In composite state entanglement, the interactions between two or more systems are complex and generally weaker than pure state and mixed state entanglement. For example, the state changes of particles in different states are complex, and their interactions are relatively weak.

These three types of quantum entanglement have significant physical significance and practical applications. In fields such as quantum computing, quantum communication, and quantum key distribution, entanglement is one of the key technologies for realizing quantum information processing and communication.

2.3. Measurement of Entanglement

Entanglement can be measured using the entanglement degree of quantum states. The entanglement degree is a numerical value that represents the degree of entanglement of a quantum state. When the entanglement degree between two quantum systems is 1, they are maximally entangled, and when the entanglement degree is 0, they are unentangled.

Quantum entanglement is a crucial concept in quantum mechanics that describes non-classical quantum correlations between two or more particles. In an entangled state, the states of two or more particles are closely connected, even if they are spatially separated by a significant distance, exhibiting a mysterious connection.

To quantify the degree of quantum entanglement, measures such as entanglement entropy or Schmidt decomposition are introduced. The entanglement entropy is a measure used to quantify the degree of entanglement between two or more particles. It is used to measure the degree of entanglement between two or more particles and the strength of their correlations in certain aspects. If the entanglement entropy between two or more particles is 0, they are unentangled, whereas if it is positive, they exhibit quantum entanglement.

Schmidt decomposition is another commonly used method to describe quantum entanglement. It is a mathematical decomposition method that decomposes a multi-particle wave function into a tensor product of two single-particle wave functions. This decomposition is used to describe the entanglement relationship between two or more particles. Schmidt decomposition decomposes a multi-particle wave function into a tensor product of two single-particle wave functions, which describe the degree of entanglement between two particles.

The measurement of entanglement is of great importance in applications such as quantum information processing and quantum communication. For example, in quantum cryptography, quantum entanglement can be used to construct protocols for secure communication. In quantum computing, entanglement can be used for communication and control between qubits, enabling quantum computation. Therefore, the measurement and application of entanglement have significant theoretical and practical significance.

In quantum mechanics, especially in quantum information theory, linear entropy is a commonly used low-order approximation of von Neumann entropy. In quantum mechanics, especially in quantum information theory, linear entropy is defined as the density matrix of a system. According to the definition, the linear entropy ranges from 0 to 1, where d is the dimension of the density matrix. Some researchers define the normalized linear entropy as a measure of entanglement dimension in composite systems. It also reflects the effective entanglement dimension in entangled states, making it an important measure of quantum entanglement. It has significant applications in studying quantum coherence in multi-particle quantum systems and other quantum information processing tasks.

The term “pure state” appears in various fields, including quantum mechanics in physics and functional analysis theory in mathematics.

In quantum mechanics, a pure state is composed of an ensemble with identical statistical properties, while a mixed state, in contrast to a pure state, can be decomposed into more than two ensembles. In quantum mechanics, various formalisms exist to represent quantum states, such as density matrices or density operators, which distinguish between pure and mixed states.

2.4. Entanglement Operations

LOCC is a method used in quantum information to manipulate quantum states. In simple terms, when a quantum system is divided into many parts, measurements and operations are limited to each individual part, while classical communication is allowed between the parts. LOCC refers to a common set of operations in the study of quantum information theory, specifically used to describe interactions between separated subsystems [6].

Specifically, LOCC operations consist of the following elements:

1. Local single-party operations: Quantum logic gates or measurements performed on each individual subsystem.

2. Classical communication: Exchange of classical information, such as measurement results, between subsystems.

3. Coordination of local operations: Subsystems can coordinate and adjust local operations based on received classical information.

4. Absence of non-local operations: Subsystems cannot perform joint global quantum operations.

LOCC operations correspond to distributed quantum information processing in practical applications, where communication between nodes is limited to classical channels. Many quantum information processing tasks can be achieved using LOCC operations, such as quantum cloning and quantum secret sharing. However, there are tasks, such as quantum teleportation, which cannot be accomplished using LOCC [7].

Entanglement control is an important concept in the field of quantum information science, involving the generation, transmission, manipulation, and measurement of quantum entanglement. In entanglement control, researchers use specific operations and control methods to create interactions between two or more particles in a quantum system, making their states correlated with each other. This correlation is highly valuable in quantum information processing and can be utilized for tasks such as quantum communication, quantum computation, and quantum teleportation.

In practical applications, the achievement of quantum entanglement control requires addressing various challenges, including improving the stability, scalability, and operational speed of entanglement. Currently, researchers have implemented quantum entanglement control in various physical systems, such as particle pairs, atoms, molecules, photons, and macroscopic objects. With further advancements in quantum science and technology, we can expect more efficient and stable quantum entanglement control, thereby driving the development of quantum information science.

3. Experimental Realization of Quantum Entanglement

3.1. Implementation of Quantum Entanglement in Different Physical Systems

Particle pairs: Quantum entanglement was initially observed in particle pairs, such as electrons and positrons. When two particles interact, their quantum states become entangled. This entanglement can be used for quantum communication, such as quantum teleportation, or for quantum computation, such as manipulating quantum bits. In atomic systems, quantum entanglement can be utilized for quantum storage and quantum computation. For example, ytterbium atoms can be used for quantum information storage, and cold atom systems can be employed for quantum bit manipulation. In molecular systems, quantum entanglement can be utilized to study intermolecular forces and molecular structures. For instance, entanglement in diatomic molecules can be used to investigate the dynamics and mechanisms of chemical reactions. In optical systems, quantum entanglement can be utilized for quantum communication and quantum computation. For example, photon pairs can be used for quantum teleportation, and optical quantum computing can utilize the quantum states of photons [8-10]. Although quantum entanglement is typically considered a phenomenon of the microscopic domain, in certain cases, macroscopic objects can also exhibit quantum entanglement. By interacting the state of a macroscopic object with microscopic particles, macroscopic quantum entanglement, known as “macroscopic quantum superposition,” can be achieved [11].

3.2. Detection and Proof of Quantum Entanglement

Quantum entanglement is a crucial phenomenon in quantum mechanics and can be observed and verified through experiments. The following are some methods for observing and verifying quantum entanglement.

Bell inequality experiment: Bell inequality is a criterion for testing whether a physical system adheres to local realism. By constructing experiments to test whether Bell inequalities are violated, one can determine if entanglement exists between two particles. Bell inequalities are derived based on local realism and classical correlation theories, providing constraints on classical correlations. Quantum mechanics predicts the existence of nonlocal quantum correlations between entangled particles, allowing for correlations that exceed the upper limit imposed by classical correlations. By designing experiments to detect spin/polarization correlations in different directions and collecting a large amount of measurement data, one can calculate the correlation coefficients of different quantum states and use them to test the values on both sides of the Bell inequality. If quantum correlations violate the Bell inequality, then entanglement is detected. This experiment clearly demonstrates nonlocal realism in the quantum world and validates the predictions of quantum mechanics. Different quantum inequalities can also be used to test different types of entanglement. Repeating experiments can further test the universality of entanglement effects. The experimental results showcase the nonclassical properties of quantum correlations and refute local realism’s description of quantum theory. By testing the nonlocality of quantum correlations, this experiment directly proves the existence of quantum entanglement in the microscopic world.

Interference experiment: Two entangled particles are separately sent into a Bell interferometer, and the observation of interference fringes is used to determine whether entanglement exists between the two particles (see Figure 3).

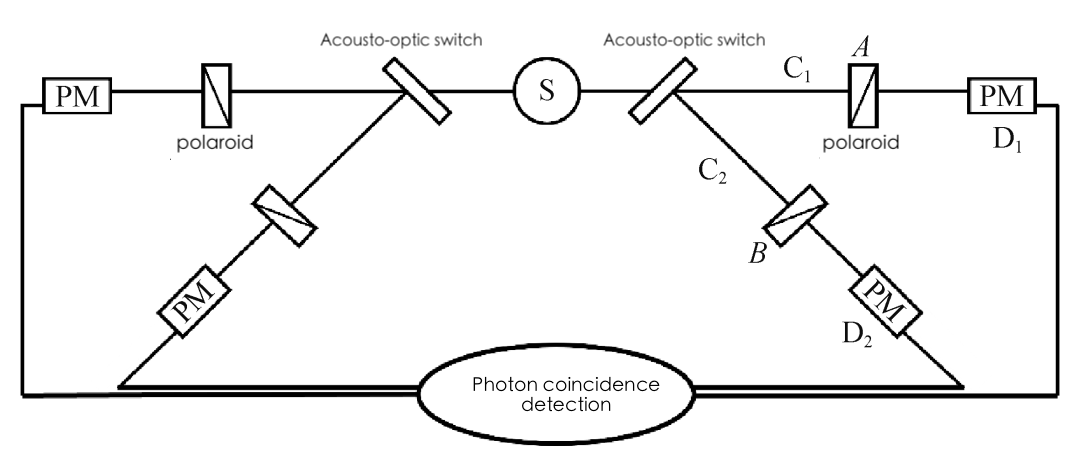
Figure 3. The experiment apparatus for Bell’s inequality[12]

Quantum entanglement between two particles is generated using methods such as Parametric Down Conversion (PDC). Different transmission channels are designed for the two particles to produce coherent superposition, and interference occurs between the two particles when they meet. If interference fringes are detected, it indicates the existence of quantum coherence between the particles. By changing the phase or path length of one of the channels, the change in interference effect in the other channel is observed. If changing one side affects the interference effect on the other side, it indicates the existence of non-local correlation between the particles. After excluding any possible classical information interaction, this non-local correlation can only originate from quantum entanglement. The experiment is repeated with different parameters to test the universality of this quantum correlation effect. The observed violation of Bell’s inequality between the two particles demonstrates their quantum entanglement characteristics. Compared to other methods, quantum interference experiments can more intuitively demonstrate the non-local effects of quantum correlation. Quantum interference experiments have become an important means for detecting frontier research on multi-particle quantum entanglement, allowing for the intuitive and effective examination of the existence of quantum entanglement states and revealing the non-local reality of the quantum world (see Figure 4).

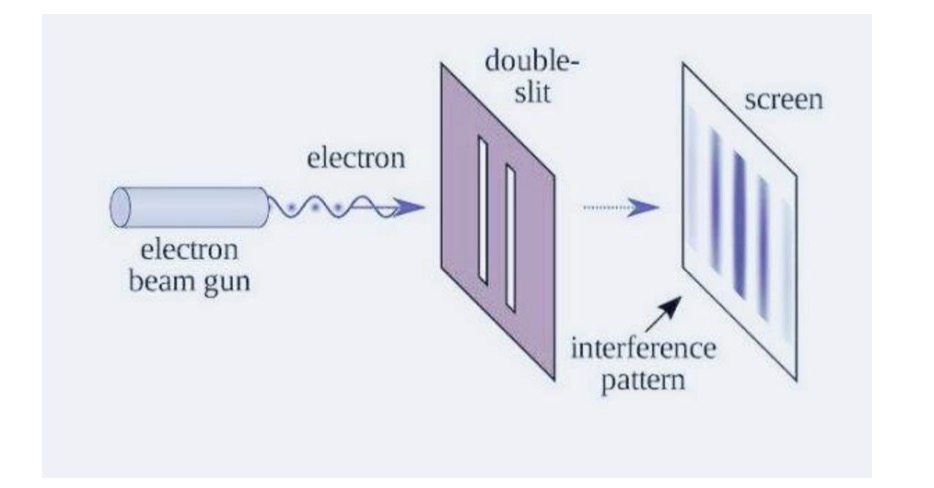
Figure 4. The experimental apparatus for interference experiments

Quantum state swapping experiments involve the interaction of two qubits after entanglement is generated. One of the qubits interacts with a third-party qubit, and then it interacts with the other qubit. At this point, it is observed that the transfer between the first two qubits is instantaneously completed without any time delay, demonstrating the existence of quantum entanglement between the two qubits. Quantum state swapping experiments are important means to demonstrate the existence of quantum entanglement. In this experiment, two pre-entangled qubits A and B are prepared, which are entangled with two independent qubits C and D, respectively. Then, a quantum state swapping operation is applied between A and B. If there is no entanglement between A and B, after the swapping, A should only be entangled with D, and B should only be entangled with C. However, the experimental measurement results show that there is still entanglement between A and C, as well as between B and D after the swapping. This proves that there must be quantum entanglement between A and B before the swapping, otherwise, the quantum state after the swapping cannot be explained. The experiment rules out any classical explanations and demonstrates the essential existence of quantum entanglement between the qubit pairs undergoing the swapping. Quantum state swapping experiments can also be extended to the case of multi-particle systems, becoming an important experimental method for detecting complex multi-particle quantum entanglement. This experiment intuitively and clearly demonstrates the existence of quantum entanglement, revealing the non-classical nature of the quantum world. Quantum state swapping experiments provide direct and reliable evidence for the existence of quantum entanglement and are one of the important experimental methods in quantum information science. This experiment reveals the non-local reality of the quantum world and has significant implications for understanding and applying quantum entanglement.

The entanglement density matrix experiment utilizes the concept of quantum-mechanical mixed states in quantum chemistry to achieve entanglement of single particles. By mixing the entangled states of two single particles, the entangled state of two particles can be obtained. In quantum information science, the non-locality of the entanglement density matrix serves as a powerful tool to prove the existence of quantum entanglement. For a quantum entangled state, its density matrix contains complete quantum correlation information. When a quantum state is completely separable and not entangled, its density matrix satisfies separability, which means it can be decomposed into the tensor product of subsystem density matrices. However, for a truly entangled quantum state, its density matrix no longer satisfies separability but exhibits non-local holistic properties. This represents the quantum-mechanical non-classical correlation between subsystems. This inseparable density matrix is the evidence of quantum entanglement. By designing different quantum states and testing the separability of their density matrices, quantum entangled states can be distinguished from classically correlated states. For example, the Bell basis test utilizes this approach. The non-separability of the entanglement density matrix provides a theoretical foundation for the existence of quantum entanglement. This density matrix-based method becomes a general approach to prove multi-particle quantum entanglement effects. In conclusion, the non-separability of the density matrix reveals the non-local nature of the quantum world and serves as strong evidence for the existence of quantum entanglement.

4. Applications of Quantum Entanglement in Quantum Information

This section provides a detailed overview of the applications of quantum entanglement in achieving deterministic quantum communication, secure key distribution, and constructing large-scale quantum networks, elucidating the core role of quantum entanglement in realizing revolutionary quantum communication.

4.1. Quantum Teleportation

Quantum teleportation utilizes the principles of quantum entanglement and indistinguishable local subsystem states. Information is encoded on one of the entangled photons and transmitted to the other photon. At the receiving end, Bell state measurements are performed without obtaining any information until the measurement basis is disclosed by the sender for decoding. This achieves secrecy in information transmission. Quantum teleportation is a key technology for realizing long-distance and large-scale quantum communication networks. Currently, low error-rate short-distance quantum teleportation has been achieved. In the future, long-distance and low-loss quantum communication can be realized. The current research focus is on achieving long-distance and high-efficiency quantum teleportation and network integration with existing communication networks. Quantum teleportation will play an important role in future quantum internet (see Figure 5).

Quantum teleportation, also known as quantum remote state preparation, quantum teleportation, quantum remote transmission, or quantum remote transfer, is a technique that transfers quantum states to arbitrary distant locations using entangled quantum particles and the transformation of physical information. It is a new form of communication. Quantum teleportation does not involve the transfer of any matter or energy. This technology is highly helpful in quantum information and quantum computing. However, it cannot transmit conventional information and cannot be used for superluminal communication. Quantum teleportation is not related to the concept of “teleporting” objects - it cannot transfer the system itself or be used to arrange molecules to form objects at the other end.

Figure 5. Comparisons of Quantum Teleportation and Conventional Teleportation

4.2. Quantum Key Distribution

Quantum key distribution (QKD) is a method that utilizes the principles of quantum mechanics to ensure communication security. It enables two parties to generate and share a random and secure key for encrypting and decrypting messages. One of the most important and unique properties of QKD is that if a third party attempts to eavesdrop on the key, the communicating parties will be alerted. This property is based on the fundamental principles of quantum mechanics, where any measurement on a quantum system will cause disturbances [13]. To eavesdrop on the key, the third party must measure it in some way, and these measurements will introduce detectable anomalies. By transmitting information using quantum superposition or entanglement, the communication system can detect the presence of eavesdropping. When the eavesdropping is below a certain threshold, a secure key can be generated. The security of QKD is based on the fundamental principles of quantum mechanics, while traditional cryptography relies on the computational complexity of certain mathematical algorithms. Traditional cryptography cannot detect eavesdropping and therefore cannot guarantee the security of the key.

In quantum communication, messages are encoded as quantum states, or quantum bits (qubits), whereas in classical communication, messages are encoded as bits. Typically, photons are used to prepare quantum states. Quantum cryptography utilizes the properties of quantum states to ensure security. There are different implementations of QKD, which can be categorized based on the specific properties of the utilized quantum states [14].

Unlike classical physics, measurement is an inseparable part of quantum mechanics. Generally, measuring an unknown quantum state will change the state of the quantum system in some form. This is known as the uncertainty of quantum measurement, and it has some fundamental implications such as Werner Heisenberg’s uncertainty principle, the theory of information disturbance, and the no-cloning principle. These properties can be exploited to detect any eavesdropping during the communication process (as eavesdropping inevitably requires measurement). Furthermore, it is possible to calculate the number of intercepted messages.

Two or more quantum states can be entangled, creating a connection such that they are considered as a whole quantum state rather than independent entities, regardless of their distance. This is known as quantum entanglement, where, for example, measuring one of the entangled quantum states will affect the other states [15]. If the entangled quantum pairs are held by the communicating parties, any interception of the message will alter the entire system, leading to the detection of the presence of a third party (as well as the quantity of intercepted messages).

4.3. Quantum Secure Communication

Cryptography can be divided into two major categories: symmetric cryptography and asymmetric cryptography. Symmetric cryptography refers to techniques where the same key is used for encryption and decryption, such as DES and AES. Asymmetric cryptography, on the other hand, uses a pair of different keys (public and private keys) for encryption and decryption, such as RSA and ECC. The advantage of symmetric cryptography is its speed and efficiency, but it requires pre-sharing a key between the communicating parties, which can be vulnerable to eavesdropping or interference. The advantage of asymmetric cryptography is that it does not require pre-sharing a key, but it is slower, less efficient, and its security relies on the intractability of mathematical problems. If someone discovers a faster or more efficient algorithm or possesses a more powerful computer (such as a quantum computer), asymmetric cryptography may be compromised. Quantum encryption is the use of quantum physics principles to perform encryption tasks. The most prominent and mature application of quantum encryption is quantum key distribution (QKD).

QKD is a technique that utilizes photons (the smallest unit of light) as carriers of information to transmit a random binary sequence (a string composed of 0s and 1s) between two communicating parties as a shared key for subsequent symmetric encryption communication (such as AES). QKD has two important characteristics: firstly, the binary sequence generated and transmitted by QKD is completely random, and neither party knows its specific content. Only after communicating through a public channel (such as a telephone or email) can they determine which bits can be used as the shared key. This avoids the risks associated with pre-shared keys.

Secondly, QKD exploits the quantum properties of photons, such as uncertainty and unclonability. If a third party attempts to eavesdrop or interfere with the transmission of photons, the photon states will change, and these changes will be detected and rejected by the communicating parties. This ensures that there is no eavesdropping or tampering during the transmission.

Therefore, QKD can achieve unconditionally secure key distribution, meaning it does not rely on any mathematical assumptions or computational complexity, but solely relies on the laws of physics. Even in the future, with the advent of more powerful computers or algorithms, QKD cannot be cracked.

4.4. Long-Distance Quantum Communication

Long-distance quantum communication refers to the technology of transmitting quantum information over long distances. Compared to traditional communication methods, quantum communication offers higher security and stronger resistance to interference because it utilizes quantum states as carriers of information instead of classical bits. In long-distance quantum communication, quantum key distribution (QKD) is one of the important technologies. QKD allows two communicating parties to generate and share a random key for encrypting and decrypting the communication content. Due to the unclonability of quantum states, any attempt by a third party to eavesdrop on quantum information during the communication process will be immediately detected by the communicating parties. Currently, significant progress has been made in China in the field of long-distance quantum communication. In 2016, China successfully launched the world’s first quantum science experimental satellite “Micius,” achieving quantum communication between the satellite and the ground. In addition, Chinese scientists have also achieved long-distance quantum communication based on optical fibers and free space, with the furthest transmission distance of optical fiber quantum communication reaching 615 kilometers [16]. Although breakthroughs have been made in long-distance quantum communication technology, many challenges need to be overcome before commercial applications can be realized, such as improving the speed of quantum communication, reducing costs, and enhancing system stability. With the continuous development of science and technology, long-distance quantum communication is expected to provide a more secure and reliable means of communication for humanity in the future.

Ground-based fiber-optic quantum communication networks refer to communication networks that utilize optical fibers on the ground for quantum information transmission. Fiber-optic quantum communication has advantages such as high transmission speed and long-distance transmission. However, in practical applications, factors such as fiber loss and dispersion require the use of technologies like quantum amplifiers and quantum repeaters to improve communication quality and transmission distance. Satellite-based and airborne free-space quantum communication refers to quantum communication conducted in free space using satellites and aircraft as carriers. Free-space quantum communication can overcome the limitations of ground-based fiber communication and achieve global-scale quantum communication. However, due to factors such as atmospheric effects and the curvature of the Earth, free-space quantum communication suffers from significant transmission losses, requiring the use of high-sensitivity quantum receivers and quantum entanglement technologies to improve communication quality and transmission distance. Quantum repeaters and memories are key technologies in long-distance quantum communication. Quantum repeaters can be used to extend the transmission distance of quantum communication by repeating quantum signals multiple times to reduce signal [17].

5. Challenges and Prospects

5.1. Challenges in Quantum Entanglement Technology

Quantum entanglement technology currently faces several challenges in the following areas: precise preparation and control of quantum states are key to quantum entanglement technology. However, due to the high fragility of quantum states, achieving stable and controllable entangled states remains challenging. In quantum communication, there is significant loss in the transmission of entangled states, especially over long distances. Improving the transmission efficiency and stability of quantum entanglement is a pressing issue. Quantum entanglement detection is an important aspect of quantum entanglement technology. Current detection methods, such as interferometers, may be affected by various noise and interference, leading to a decrease in accuracy. Most current experiments on quantum entanglement are based on specific quantum systems, such as photons and ion traps, making the implementation of multi-particle entanglement and operations still challenging. Despite significant progress in theoretical research, quantum entanglement technology still faces many practical issues, such as system stability and operational complexity. The practical application of quantum entanglement technology remains an important challenge. Although quantum entanglement technology can be used for secure communication methods like quantum key distribution, the security of quantum entanglement itself requires further research and verification. In summary, quantum entanglement technology still faces numerous challenges in practical applications. These challenges need to be gradually overcome through scientific research and technological innovation to achieve the widespread application of quantum entanglement technology.

5.2. Prospects and Trends in Quantum Entanglement

The deep nature of quantum entanglement is a highly complex problem, and the physics community has different perspectives on it. The following viewpoints exist: (1) Quantum entanglement is a fundamental characteristic of quantum mechanics, reflecting the holistic and non-local nature of quantum systems. It reveals the essential difference between the microscopic and macroscopic worlds. (2) Quantum entanglement reflects a deeper reality and embodies more profound physical laws. Some believe it is related to virtual particles and vacuum fluctuations. (3) Quantum entanglement can be seen as a new type of interaction or information connection that transcends spatial distance limitations. (4) Quantum entanglement is related to the consciousness of observers, supporting the viewpoint of consciousness creating reality. (5) Quantum entanglement reveals a deeper nature of space, time, and causal relationships, supporting the existence of more fundamental hidden variable theories. (6) Quantum entanglement is merely a concept within the mathematical framework of quantum mechanics and should not be overly materialized. In conclusion, quantum entanglement reveals a quantum world that is distinct from classical physics, and its profound implications still require further theoretical and experimental research for clarification. The exploration of the essence of quantum entanglement is prompting us to examine the foundations of physics and even epistemology.

In the future, quantum entanglement technology will have several development trends:

Quantum communication, including quantum key distribution, entanglement state transmission, and quantum networks, will experience greater development.

Quantum computing, as an important branch of quantum information technology, will make significant breakthroughs in quantum bits, quantum algorithms, and entangled states.

Quantum key distribution, as an important application in quantum communication, will achieve further development in areas such as entangled states, quantum stealth transmission, and quantum cryptography.

The preparation and control of entangled states, which are key to quantum entanglement technology, will witness the emergence of more efficient, stable, and controllable techniques.

Quantum entanglement technology will not only have application value in quantum communication, quantum computing, and quantum key distribution but also find applications in other domains such as quantum sensing, quantum simulation, and quantum control.

In summary, quantum entanglement technology will play an increasingly important role in future development and have a profound impact on human society.

6. Conclusion

This paper has focused on the development of quantum entanglement and the challenges it faces, from its origin to its scientific applications and subsequent issues. We have provided a definition of quantum entanglement and discussed the factors to consider, the aspects that need to be proven, and the aspects that require proof in the application of quantum entanglement. Quantum entanglement is still not fully understood and has ample room for further development. From the birth of the EPR paradox to the proposition of Bell inequalities, and to the subsequent proofs of the existence of inequalities in the 21st century, humanity is gradually exploring the field of quantum entanglement and other quantum domains. We believe that in the near future, there will be significant breakthroughs in the related fields of quantum entanglement.