

Volume 4 Issue 3
Published on November 2025A mathematical framework is presented to quantify the relationship between quaternary-structure symmetry, free energy, and catalytic efficiency during the transition from aD2-symmetric tetramer to aC2-symmetric dimer, exemplified with LDHA. The approach constructs explicitD2representations on subunit and interface feature spaces, derives projection operators to decompose operators and data into irreducible-representation components, and computes symmetry-resolved free-energy differences via Gaussian/statistical and harmonic/Hessian methods. Connections to kinetics are made through transition state theory with channel degeneracy. Reproducible algorithms and a workflow for mapping FoldX outputs into irrep-resolved diagnostics and efficiency predictions are provided.

 View pdf
View pdf


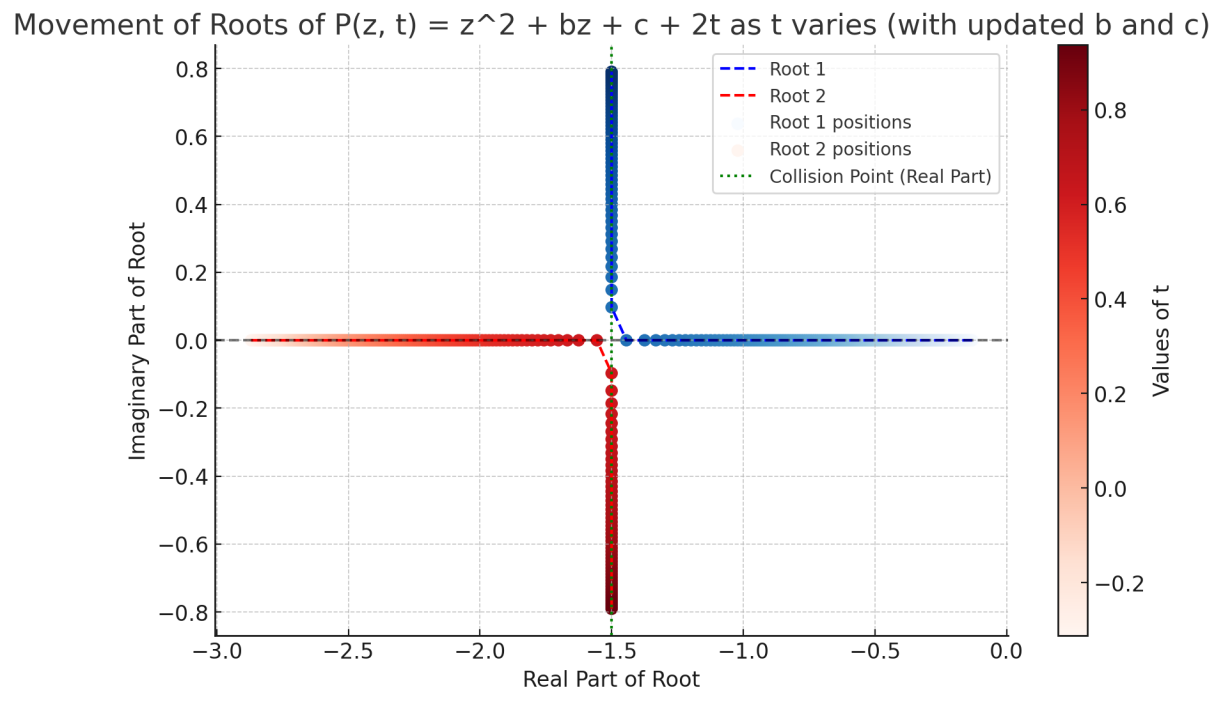
Deformation of polynomials is a kind of operation where we add a new variable to the original polynomial. In our case, suppose P is a monic polynomial of degree n with complex coefficients. We evolve P with respect to time by heat flow, creating a function P(t,z) of two variables with given initial dataP(0,z)=P(z)for which∂tP(t,z)=∂zzP(t,z). In this paper, we focus on the deformed polynomial P(t,z). First, we proved the Taylor series representation of deformed polynomial. Then we apply the results to the classical Hermite polynomials and extend to the case of matrix-valued polynomials. From the inspiration of deformed polynomials’ roots movement, we proved the behavior of Hermite polynomials after heat flow deformation and got an explicit formula. For further work, similar to what we have done in this paper, we want to have an explicit formula for deformed matrix Hermite polynomials and give a proof.

 View pdf
View pdf



Renewal theory originated from research on component failure and replacement. It has since developed into a key framework for analysing systems of repeated events within applied probability. This paper reviews the key concepts and principal findings in this field, while demonstrating several of its applications. The paper first introduces the Poisson process, highlighting the inter-arrival intervals of the exponential distribution and its 'memorylessness’, thereby introducing the general renewal process. The renewal function, elementary renewal theorem, renewal equation, and key renewal theorem are discussed, with attention to their assumptions, interpretations, and asymptotic conclusions, showing how they can be applied. The paper also presents several practical extensions of the renewal processes, including the delayed renewal process, renewal reward process, alternating renewal process, and age-dependent branching processes. Finally, concise examples illustrate the computation of long-run replacement and success rates, as well as the use of demographic renewal equations. Applications in reliability, service operations, and demography show that renewal models provide transparent asymptotic rates and availability with modest modelling complexity.

 View pdf
View pdf




