1. Introduction

The internet today is a vast repository of information, merchandise, and opportunities. On one hand, users are confronted with more choices than ever before. From selecting a restaurant for an anniversary date to searching for trip accommodations for the summer vacation, users are burdened with information overload. On the other hand, service providers need to predict potential users' feedback or ratings on certain items from a wealth of information to plan business arrangements and resource allocations. Recommender systems serve to provide customized recommendations to both sides of this picture.

Despite the abundance of data, traditional recommender systems [1] are detached from social embedding. As a result, business providers still suffer from issues such as cold-start and data sparsity, which adversely affect prediction accuracy. Additionally, users struggle to understand if the recommended merchandise matches their true interests. In this context, some have proposed social network-based recommender systems to tackle the lack of structure and correlation in sparse user and item data sets.

It is natural to imitate the decision-making process during which people seek advice from close friends or trusted sources, as tastes and preferences tend to be highly overlapped. Furthermore, social network embedding means more than seeking advice from close friends, as close friends may share similar tastes but may not have overlapping experiences, causing inconsistency issues in the user-item dataset. The social network gathers information from higher-order social links, which is generally beneficial to embed these social influence factors into the recommender's decision-making process, thereby alleviating the problems of traditional approaches.

It has been established that integrating social networks into the recommender system will alleviate the disadvantages of traditional methods in both user-level and item-level [2]. Recent state-of-art approaches on social network enhanced recommendation tasks with novel deep learning approaches such as [3-6] show considerable improvements in prediction accuracy compared to traditional approaches, such as SVD++ [7]. One of the inspiring contributions they [4,5] made, is simulating user's decision-making process with a deep social influence propagation model, with a layer-wise recursive diffusion structure. In spite of the better performance compared to previous approaches, it has been observed that the performance decreases with higher diffusion depth K > 2, which limited the versatility and data efficiency of the model.

In this work, we propose to improve the performance of the state-of-art social recommendation system, Diffnet [4] and Diffnet++ [5], by implementing novel structures associating with the homophily effect in the heterogeneous graph of Diffusion Layer, and adding weighted embedding method in the Prediction Layer. Our research investigates how to enhance social network-based recommender systems using probabilistic graphical models, with data from Yelp and Flickr. We compared our model to the state-of-the-art social recommendation systems Diffnet and Diffnet++. Our improved Diffnet++ model integrates higher-order social structure and interest network information through a weighted diffusion layer, as proposed by Wu et al. [5]. Empirical results, measured by Normalized Discounted Cumulative Gain (NDGG) and Hit Ratio (HR) metrics, demonstrate the effectiveness of our weighted strategy. Additionally, we introduced the homophily effect in the diffusion layer, leveraging similarity networks based on latent user embeddings to incorporate information from both social and similarity networks for better recommendations. Our approach outperforms competitive baselines.

2. Literature Review

Our paper is related to two streams of research, namely, recommender system and differentiation between homophily effect and social influence effect.

2.1. Recommender System

There has been a significant amount of research employing probabilistic graphical models (PGM) to optimize recommender systems. For example, Anaya, Luque, and García-Saiz [8]. developed an Influence Diagram (ID), an extension of the Bayesian Network (BN), within the context of student collaborative learning. Integrating decision variables, student preferences, and hidden variables impacting student behavior, the authors utilized an attribute selector and decision tree to access and interpret the ID. Ultimately, they provided the optimal policy and corresponding explanations for such recommendations. Additionally, Rho and Cho [9] also proposed a recommender system utilizing PGM. They built a modularized BN that is aware of the mobile phone context and can provide an optimal recommendation of mobile APPs. Their model accuracy and F1-score have been proved high when applied to empirical data. Apart from directly using PGM as the recommender system framework, He and Chu [10] have incorporated PGM to account for user relations in the traditional matrix-based recommender system, so that the problem of sparse user/item rating matrix can be solved. Specifically, they built a graphical model to represent a delicate social network that can’t be easily summarized by similarity matrix and then used it to infer user preference influenced by immediate and distant friends. Improvement in prediction accuracy is proved by experiments.

In recent years, the significant advancements in deep learning and the substantial growth of data have led to increased interest in neural network-based approaches for recommendation tasks. Among these, graph neural networks (GNN) have demonstrated superior performance due to their ability to learn structural information and their compatibility with multi-source data in recommender systems. Consequently, novel GNN-based systems have been developed, incorporating external data such as social networks and knowledge graphs. Compared to traditional approaches, GNNs enhance the representation of users and items by capturing higher-order latent information embedded in the graph. Numerous GNN-based approaches have been proposed in recent years. For instance, GraphRec [3] utilizes user-item interactions and social networks for user modeling. DiffNet [4] employs social networks to improve user representation through layer-wise influence propagation structures. An improved version, DiffNet++ [5], was later introduced to further model user-item interests within the user representation. Additionally, DANSER [6] applies the attention mechanism on graphs to model the dual effects of user/item homophily and influence.

2.2. Differentiation between Homophily Effect and Social Influence Effect

A significant body of research has explored the challenge of differentiating between social influence and homophily. Social influence refers to the process where an actor in the network affects its neighbors' decisions, while homophily denotes the phenomenon where similarities between nodes lead to similar or correlated outcomes among neighbors. Various methods have been employed to address this issue, with some studies using data-driven randomization tests [11] and others focusing on model specification [12]. Our interest lies more in the latter approach. Aral, Muchnik, and Sundararajan [13] have proposed a matched sampling method to overcome the selection biases of regression analysis by comparing nodes that have the same likelihood to have (but actually have not) been connected to the same number of friends, conditional on their demographic features. However, these are all based on observed characteristics which cannot address unobserved heterogeneity among consumers. Thus, Ma, Krishnan, and Montgomery [14] differentiate the effect of unobserved homophily from social influence using a Bayesian framework. In this framework, the static homophily effect is distinguished from the dynamic social influence effect through a hierarchical parameter specification. They set evidence of homophily as the variance of the multivariate normal distribution of the social influence parameter. Some scholars use the fixed number of in-degree as an exogenous constraint [15] and focus on the endogenous dynamics of link formation, based on a dynamic social network structure where out-degree follows a Poisson distribution [16]. Zhang, Pavlou, and Krishnan [17] use a hierarchical Bayesian autoregressive mixture model called mNAP [18] to differentiate the effect of cohesion (similar to social influence) from positional equivalence (positional homophily) on binary outcomes, where the parameters of two network influence terms enter the latent preference of individuals to further influence adoption decisions.

3. Dataset

We propose to use the Yelp academic dataset, which was collected from eight metropolitan areas such as Montreal, Toronto, and Pittsburgh over 1.2 million businesses and over two million users. To help explore the hidden structure behind everyday business activities and interactions between users and service providers, Yelp provides several types of data: business, review, user, check-in, tip, and photos. We are particularly interested in its user data because it includes not only attributes related to the user's profile and a summary of their interactions with local businesses, but also friend mapping that shows the relationships between users.

Flickr is an image/videos based social sharing website, featuring a social network in which each user shares preferences to images/videos to her social followers, and can express preferences through the upvote behavior. The reason to adopt Flickr as dataset is that compared to Yelp, it shows higher social connections as shown in “Link Density'” in Table 1. This might provide some insights into how different social network attributes affect the overall performance of the algorithms.

Table 1: Summary Statistics of the Yelp and Flickr Dataset.

4. Baseline Model

Through literature search and preliminary data analysis, we found that the performances of a lot of recommendation systems are unsatisfactory and largely limited by the sparseness of user-item interaction data. In addition, it has been proven to be effective to improve recommender performance with social-network embedding. However, most of the related works only took advantage of the first-order local neighbors in the users' social network. These approaches often find obstacles in further improvement in the accuracy of prediction of user's future preference, as those static models usually find it hard to leverage matrices representing social connections that are typically even sparser than the user behavior data. Some argue that users in a social network can be affected by not only her trusted users but also the influences propagated from her trusted users' social connections in a dynamical way. Therefore, we have found it particularly beneficial to adopt a social influence propagation process featuring some recursive dynamics of interest diffusion inside the social network, proposed in DiffNet [4] and DiffNet++ [5].

4.1. Objective

When discussing a social recommender system, we usually start with two entities: m users in a set U and n items in a set V. To avoid confusion, in all the formulas and figures, users are denoted as u_a, u_b, u_c and items denoted as v_i, v_j, v_k. Besides, each user is also associated with a vector of d_u real-valued user attributes x_a, which is a columns of matrix X ∈ ℝ^{du × m}.

Similarly, each item is associated with a vector of d_v real-valued item attributes y_i which is a column of matrix Y ∈ ℝ^{dv × n}. The interactions can be categorized into two types: user behavior matrix R ∈ ℝ^{m × n} relates users and their individual preference on each specific item, and social network matrix S ∈ ℝ^{m × m} showing users' social connections. Then, a preference matrix is predicted as follows:

\( \hat{R}=f(X, Y, R, S) \) ,(1)

which can be parsed into some ranking list R_a of N (a hyper-parameter) items for each user in a typical online recommendation scenario.

4.2. Diffnet

Diffnet proposed a deep influence propagation model to simulate the recursive diffusion process in which users find common grounds with their social connections, seek for advices and make decisions. There are three steps in this approach:

Embedding. For a user u_a, an initial embedding links the relevant features with a free latent vector p_a that encapsulates the latent behavior preferences. Furthermore, a fusion layer takes the user's original attributes vector x_a and latent vector p_a into a new user fusion embedding:

\( h_{a}^{0}=g({W^{0}}×[{x_{a}},{p_{a}}]) \) ,(2)

Each item will also have its corresponding latent vector, but it does not participate in the diffusion process.

Diffusion. As the key component of this model, a layer-wise influence propagation structure of diffusion-depth K depicting the evolution of user's latent embedding as the social diffusion process continues.

Prediction. After the diffusion process, a final latent representation u_a is composed from the embeddings collected from the diffusion layers' output as h_a^k and the preferences from her historical behaviors as \( \) . Then the prediction can be simply measured by the inner product between the computed final user's latent representation and the item's latent vector.

4.3. Diffnet++

On the basis of Diffnet which only models the influence diffusion process in the social network, Diffnet++ is an improved algorithm that unifies the influence aggregation of social networks with interest aggregation of item neighbors from the user-item network in a heterogeneous graph.

In this model, each user's fusion latent vector u_a propagates through the diffusion layers with updates from combination of both influence diffusion aggregation \( \widetilde{p}_{a}^{k} \) and interest diffusion aggregation \( \widetilde{q}_{a}^{k} \) . It let the user play the central role in this process, while also combining two networks that mutually enhance each other in the higher-order structure. By reformulating the social recommendation as a heterogeneous graph, the model recursively learns about the user's latent embedding information from convolutions on both social influences and interest influences, which further resolves the sparsity issues in the data.

4.4. Limitation of Baseline Models

The baseline model had given better performance compared to the earlier related works [5] with its fine-tuned social/interest influence diffusion process. Nevertheless, we still found this model limited by some obstacles with a closer look at its architecture, which leaves room for further improvements in its algorithms.

First, the diffusion depth K in Wu et al. [5] shows fast increases in performance with its value turned on from 0 to 1, and it achieves optimal performance when K = 2. However, further expansion of these influence layer structures by tuning K ≤ 3 will result in decreasing performances. The authors argued from an empirical perspective that adding more layers might introduce unreliable neighbors into the latent embedding. To address this limitation, we argue that the information captured by different levels of the diffusion layer may contribute differently to the prediction, then we propose to apply adaptive weights to the embedding learned from each diffusion layer as shown in the next section.

Additionally, social network data complements ratings and preferences information, as placing excessive emphasis on either type may result in only marginal improvements in overall performance.

The authors attempted to alleviate this issue by designing a multi-level attention mechanism to fuse the social network and interest network but achieved little in further exploiting the data. Third, although the authors have got a rich dataset on user information and social networks, they only utility limited amount of information contained within the social network data, but actually further information can be included if we also take preferences of similar users into consideration.

5. Methods

Given the limitations of the baseline model, we proposed some extensions in the Diffusion Layer and Prediction Layer to further improve model performances on the two metrics of interest, including HR and NDCG.

5.1. Homophily Effect in the Diffusion Layer

We made an extension by simultaneously taking the homophily effect and social influence effect into consideration in the Diffusion Layer when updating the user's embedding u_a^k+1. We first calculated user similarity in the Embedding Layer based on the free latent embedding matrices of users and then constructed a sparse adjacency matrix by adding an assumed link among the top x% most similar users. In our experiments, x is treated as a hyperparameter and is fine-tuned accordingly. Then, we added the homophily effect in the Diffusion Layer to incorporate not only the social influence effect but also the homophily effect when predicting user decisions, and thus make better recommendations (Figure 1).

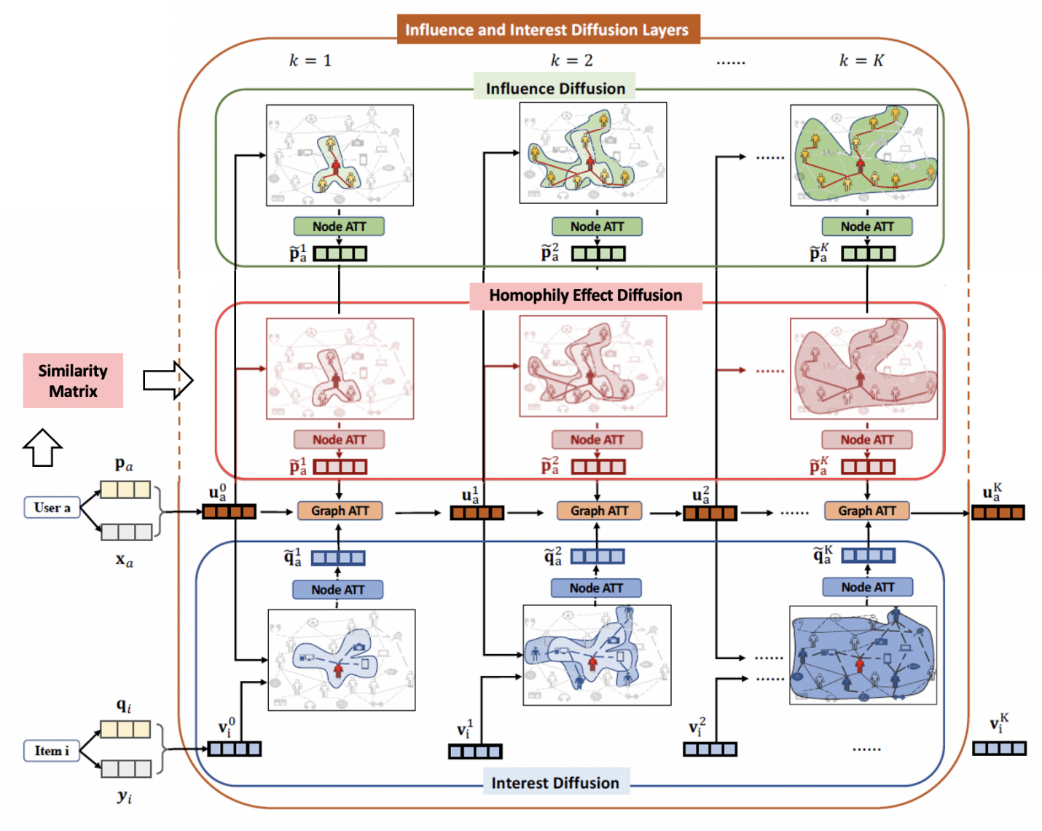
Figure 1: Diffnet++ Architecture and Possible Improvement by Adding Homophily Effect

\( u_{a}^{k+1}=u_{a}^{k}+[γ_{a1}^{k+1}(\widetilde{p}_{a}^{k+1}+\widetilde{p} \prime _{a}^{k+1})+γ_{a2}^{k+1}\widetilde{q}_{a}^{k+1}] \) ,(3)

\( \widetilde{p}_{a}^{k+1}= \) ,(4)

\( \widetilde{p} \prime _{a}^{k+1}= \) ,(5)

\( \widetilde{q}_{a}^{k+1}= \) ,(6)

where \( \widetilde{p}_{a}^{k+1} \) is the aggregated embedding of social influence effect diffusion, \( \widetilde{p} \prime _{a}^{k+1} \) is the aggregated embedding of homophily effect diffusion, and \( \widetilde{q}_{a}^{k+1} \) is the embedding of aggregated interest diffusion from the interested item neighbors at the (k + 1)-th layer. Specifically, \( α_{ab}^{k+1} \) denotes the social influence effetc of user b to a at the (k + 1)-th layer in the social network, and \( α \prime _{ab}^{k+1} \) denotes the homophily effect of user b to a at the (k + 1)-th layer in the user similarity network. Besides, \( β_{ab}^{k+1} \) denotes the attraction of item i to user a at the (k + 1)-th layer in the interest network.

5.2. Weighted Embedding in the Prediction Layer

The essential part of the recommendation system is to accurately learn the user embedding and item embedding. In Diffnet++, a diffusion layer was adopted to capture the information from the social graph and item interaction graph hierarchically. For each user a, the user embedding can be written as u_a = [u_a⁰, u_a¹, …, u_a^K] by concatenating the individual embedding vector from each diffusion layer. Similarly, the embedding for item b can be written as v_i = [v_i⁰, v_i¹, …, v_i^K]. In Wu et al. [5], they empirically set K = 2, where K refers to the depth of diffusion here. Also, they report that as K increases from 2 to 3, the performance of the model decreases, since the higher-order diffusion may capture some relatively irrelevant information in the user and item embedding. As shown in Figure 2 Diffnet++ part, the original Diffnet++ concatenates the learned user and item embedding, u_a and v_i, then perform the inner product to get the final prediction, r_ai = u_a^Tv_i.

Inspired by Mahalanobis distance in metric learning and observing the decrease in the performance of the model when setting K to a larger number [5], we consider the embedding from different levels of diffusion layers may contribute differently to the user and item information. Therefore, we proposed to adopt a weighted embedding strategy. That is, instead of directly concatenating those embedding, the model learns another two sets of weights for the user and item embedding, the weighted embedding can be written as u_a^* = k_a ⊙ u_a and v_i^* = l_i ⊙ v_i. The predicted rating then becomes r_ai = u_a^*Tv_i^*. Note that this is equivalent to using only one set of weight, z_ai, inside the inner product as

\( {r_{ai}}=\sum _{j=1}^{K}z_{ai}^{j}u_{a}^{j}v_{i}^{j} \) .(7)

However, we believe that designing separate weights for users and items will enhance interpretability.

5.3. Metrics

For the top-N evaluation, we use the same metrics as in Wu et al. [5], HR and NDCG. HR refers to the percentage of hits in the top-N list

\( HR =\frac{\ \ \ hits}{N} \) . (8)

Besides, NDCG measures the quality of the top-ranking items:

\( DCG=\sum _{i}^{N}\frac{{rel_{i}}}{log(i+1)} \) ,(9)

\( NDCG=\frac{DCG}{IDCG} \) , (10)

where IDCG (abbreviation for Ideal Discounted Cumulative Gain) refers to the maximum possible DCG (abbreviation for Discounted Cumulative Gain) value, rel_i refers to the relevance of the i-th item ranking. Following Wu et al. [5], for one user, 1000 unrated items are randomly chosen as pseudo-negative samples. Next, the pseudo-negative samples and the user's positive-rated samples are mixed as a pool for the recommender to select top-rated candidates.

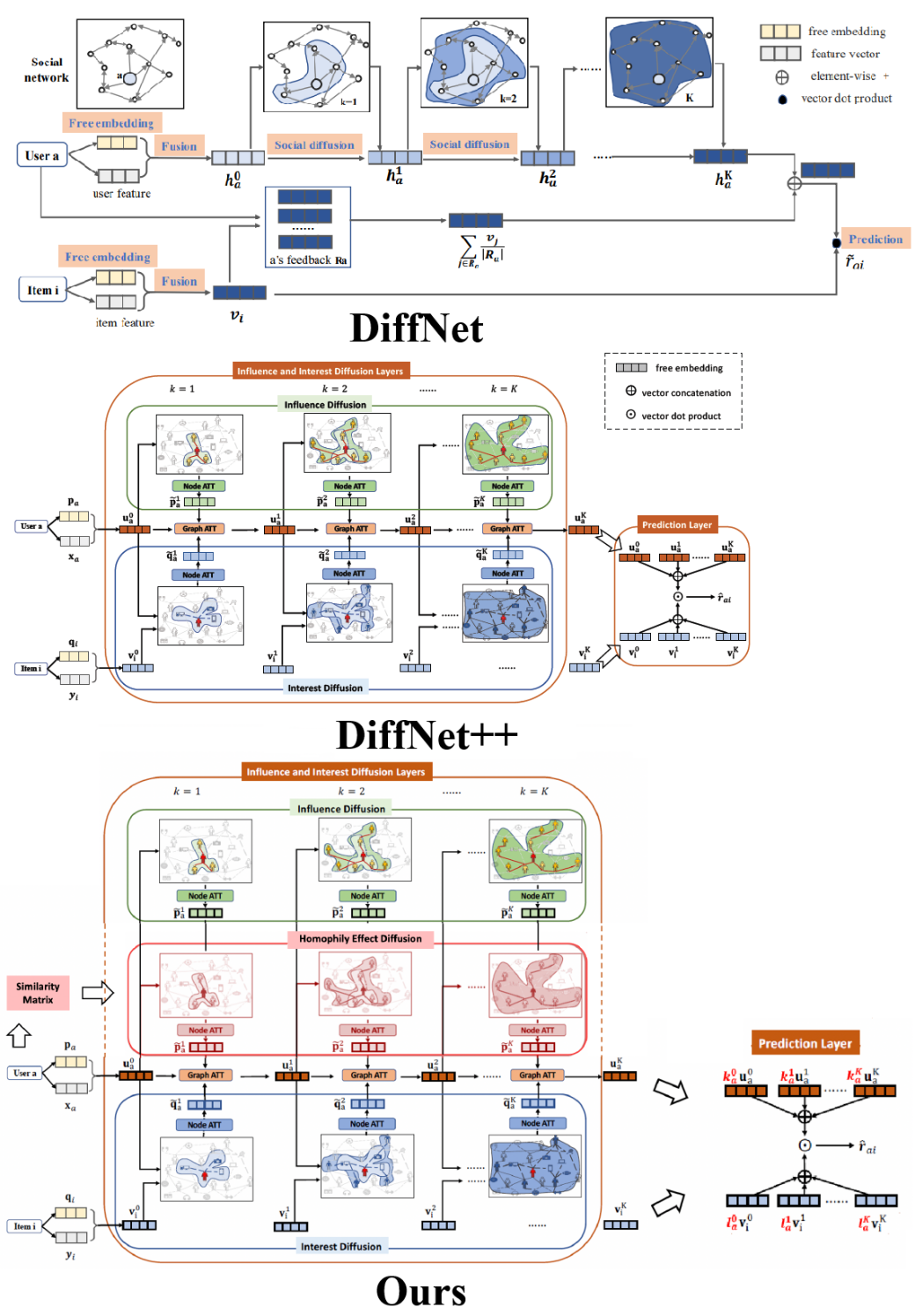
Figure 2: Diffnet++ Architecture and Possible Improvement

6. Experiment

6.1. Model Performance Comparison

The comparisons of the proposed approach with other baseline approaches are shown in Table 2 and Table 3 for Yelp and Flickr data sets. Note that the results of our proposed method are from our implementation, and the results of other approaches are re-used from Wu et al. [5]. In our implementation, the models are trained for 70 epochs with a learning rate of 0.0005, and the model with the lowest loss on the validation set is selected.

Table 2: Overall Comparison with Different Top-N Values (D = 64) on Yelp Dataset.

Table 3: Overall Comparison with Different Top-N Values (D = 64) on Flickr Dataset.

6.2. Visualization of Weighted Embedding

To verify the how the weighted embedding help in the prediction, we also plot the values of the weights from the trained models on those two data sets, as shown in Figure 3. We might see that some of the weight values deviate from 1 or -1 (unweighted state), which means that the weighted embedding indeed improves the models. Also, the distribution of weight values of two models are similar but with some small differences. The values of item-weights are mostly between -1 and 1, and the user-weights are larger than 1 or smaller than -1. However, the weight values form Flickr model have more item-weights larger than 1 which differs from the Yelp model. The future work might try to interpreter the differences by addressing the input social networks and the item-wise networks.

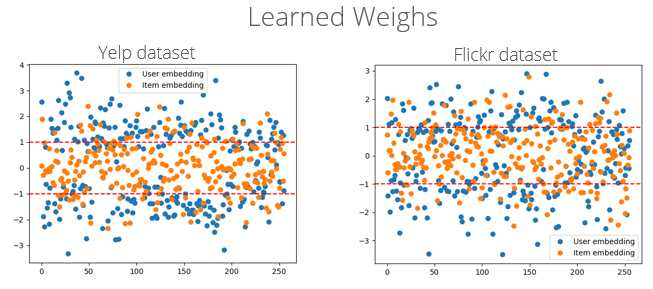
Figure 3: Weights from the Trained Models

7. Conclusion

Our research question is how to build a better social network-based recommender system using the probabilistic graphical model. We used data from Yelp and Flickr, and the baseline model we explore is the state-of-art social recommendation system (Diffnet and Diffnet++). When comparing model performance, the metrics we are interested in are NDGG and HR.

7.1. Discussion of Methods and Results

In this work, we show an improved Diffnet++ model by weighted integrating higher-order social structure and higher-order interest network information captured by the diffusion layer proposed by Wu et al. [5]. The empirical results show that the effectiveness of our proposed weighted strategy by both looking at the HR or NDCG values or learned weight values.

Besides, we contribute to the base model by further adding the homophily effect in the diffusion layer based on the similarity network calculated using the free latent embedding matrices of users, and thus more useful information of not only friends in the social network but also similar users in the similarity network can be wielded to make better recommendations.

Combining the above two improvements, our proposed approach outperforms other competitive baseline approaches as shown in Table 2 and Table 3.

7.2. Managerial Implications

In the current digital era, characterized by an overwhelming abundance of information and choices, businesses must leverage advanced recommender systems to maintain a competitive edge. Traditional recommendation systems, while data-rich, often fail to incorporate the nuanced social context essential for accurate predictions, leading to issues such as cold-start problems and data sparsity. This results in suboptimal user experiences and inefficiencies in resource allocation for service providers.

By incorporating enhancements such as the homophily effect in the diffusion layer and weighted embedding methods in the prediction layer, we have developed an improved model that leverages both social and similarity networks. This approach not only alleviates the limitations of traditional recommender systems but also ensures more precise and personalized recommendations.

For managers, this implies that investing in advanced, socially-embedded recommendation technologies can lead to better user satisfaction and higher engagement rates. Implementing such systems can improve the accuracy of predicting user preferences, optimize business operations, and ultimately drive revenue growth. As demonstrated by our empirical results, these enhancements offer a competitive advantage in the crowded digital marketplace by effectively addressing the intricate dynamics of user interactions and preferences.

7.3. Future Work

We observed that model size is crucial to the success of recommendation systems. An efficient model such as SVD++ can learn incredibly fast but tends to struggle with complex user-item and user-user dynamics. In contrast, deep neural networks can handle more complicated decision-making processes but often suffer from overfitting when applied to sparse datasets with too many layers, leading to poor predictions of users' future preferences. One potential improvement is to incorporate probabilistic estimation into the process.

To take a further step, we might also seek to develop an ensemble approach to extend the current approach to work with multi-source data. The diffusion layers in Diffnet++ can be treated as a base model. We might also learn models (like SVD++) to produce the different user and item embedding and concatenate them together with some learnable weights. Our premise is that different base model learns some distinct aspects of the user and item information, and it is compatible with the heterogeneous data source.

Acknowledgements

I acknowledge that Miss Sargent is responsible for all contents in the report, under the guidance of Miss Sargent, I am capable of managing my school study and the study of this paper, her trust and support are indispensable for me to finish this paper.

I also would like to convey my heartfelt gratitude towards Miss Fung, for helping me in the academic aspect of my research, the enlightening discussion and thought-provoking advice.

In addition, appreciate Mr Lofthouse, the house parent in my boarding, for taking care of me and providing countless encouragements with endless patience.

Finally, many thanks to my family for their unfailing love and unwavering support.