1. Introduction
With the rise of big data and artificial intelligence, there is an urgent need for an algorithm that can filter and sift a large amount of data into useful information and knowledge. In this case, data mining plays an important role [1], and frequent itemsets mining is an important branch of data mining projects and an important part of data mining [2]. In 2017, Fournier-Viger, Philippe, et al. made a corresponding investigation on frequent itemset mining [3]. Therefore, frequent itemset mining has been used in many applications, including cross-shopping [4], and traffic accident analysis [6].
However, traditional frequent itemset mining (FIM) only focuses on the case of exact matching mining, that is, the case of absolute matching. When some data in the transaction database is missing, which lead some interesting frequent itemsets will be ignored [7].
This paper mainly does the following work:
A linear list fault-tolerant frequent itemset mining algorithm based on bit combination is proposed.
Proposed deduplication algorithm and introduce the repeat structure to remove the support for repeated calculations.
2. Relate work
In 2005, Jia-Ling Kon et al. proposed a FT_Pattern mining method based on bit vector representation and described the VB-FT-Mine algorithm [8]. In 2008, Bashir, Halim, and Baig proposed an algorithm for mining fault-tolerant frequent itemsets based on a pattern-growing approach [9]. In 2014, Shengxin Liu and ChungKeung Poon proposed an effective approximate transformation of heuristic algorithms to solve problems [5] and evaluated the effectiveness of the algorithm in experiments, they proposed an acceleration technique to further improve the efficiency of the algorithm with acceptable errors [10]. In 2017, A Ashraf and T Nafis, et al. proposed an algorithm to find fault-tolerant frequent pattern mining in massive datasets containing both deterministic and uncertain records [11]. Similarly, Zhiyang Li, Fengjuan Chen, et al. proposed an algorithm for mining weighted probability frequent itemset in uncertain databases [12]. Guanling Lee and Sheng-Lung Peng et al. proposed the concept of proportional fault-tolerant frequent itemset [13].
3. Construct the bit combination data structure
Traditional FP-Tree mining algorithms need to obtain the support of candidate fault-tolerant patterns through pointers linking parent and child nodes and previous pointers in the header table. At the same time, according to the information of the header table and the previous pointer in the node, the algorithm puts the nodes starting with the same highest bit item into a horizontal chain, and the result is shown in Figure 1.

Figure 1. The result of data migration.
After data migration, the algorithm will perform fault-tolerant frequent pattern mining. Compared with the traditional algorithm, this method recursion of FP-Tree. In the following mining, the algorithm obtains the support of the candidate FT_Pattern by bitwise and operation with the nodes in the current horizontal chain according to the relevant conditions. This method reduces the execution time of the algorithm.
4. Fault-tolerant frequent itemset mining
4.1. Strategies for generating candidate FT_Pattern
The process of mining FT_Patterns is to concatenate a bit on the binary number of existing FT_Pattern, aim to obtain new FT_Candidate, and then obtain new FT_Pattern according to SUP and SUPI defined by the user.
The algorithm generates new FT_Candidate by using the formula: ans_bit [k] [hight] | 2j. Ans_bit is an integer array that holds the binary numbers of the generated FT_Pattern, k is the current FT_Pattern to be processed, hight is the highest group of binary data, j is the binary bit in which the data item concatenates 1 with the highest bit. Through the above method, the algorithm generates new FT_Patterns based on the determined FT_Pattern, reducing the number of generating FT_Candidate.
4.2. Fault-tolerant frequent itemset mining strategy
In the following, this paper will take Figure1 as an example to illustrate the fault-tolerant frequent pattern mining process. When scanning the horizontal chain of item d, the binary data of the node on the horizontal chain is operated by AND with the binary data of FT_Candidate. That is, the binary number 00011 of the first node of the horizontal chain where item d is located is compared with the binary number 00011 of FT_Candidate da, and the final result is 00011.
The algorithm increase the global support of the candidate itemset {d, a}, that is, sup(d, a) = 3, and increases the support of the item that matches successfully, that is, item_sup(da, d) = 3, item_sup(da, a) = 3.
Notice that since the binary number corresponding to entry a at this node is 1, the ancestor of this node is the element in the horizontal chain in item a. Since the algorithm will continue to mine the nodes in the horizontal chain of item d after mining the nodes in the horizontal chain of item a, the algorithm takes the following approach to prevent repeated mining: If the FT_Candidate m = {x, w, z} is in the horizontal chain of the highest item x and its ancestor is in the horizontal chain of the second highest item w, the frequency matched with the binary number of this part of nodes will be saved in repeat.
The procedure for calculating the da support of a FT_Candidate is shown in Table 1.
Table 1. The algorithm calculates the da support of fault-tolerant frequent patterns
Sup(y) | Item_sup(y, i) | Repeat(y) |
Sup(da) = 3 | Item_sup(da, d) = 3 | Repeat_sup(da) = 3 |
Item_sup(da, a) = 3 | Repeat_item(da) = 3 | |
Item_sup(da, d) = 3 > SUPI = 2 | ||
Sup(da) = 8 | Item_sup(da, a) = 8 | |
Sup(da) = sup(da) – repeat_sup(da) = 8 – 3 = 5 Sup(da) = 5 ≥ SUP = 4 | ||
Item_sup(da, a) - repeat_sup(da) = 8 – 3 = 5≥ SUPI = 2 Item_sup(da, a) = 5 ≥ SUPI = 2 | ||
da is FT-pattern, add da to FT-pattern List | ||
5. Results and Discussion
This section tests the time performance of the FT_HTlist algorithm in different types of datasets. Figure 2 and Figure 3 show the mining time and the number of frequent items in the sparse data set by setting SUP = 1% unchanged and changing the size of SUPI/SUP from 0.5 to 1 with a step size of 0.1.
It can be found that the running time of the algorithm is inversely proportional to the magnitude of the ratio. With the increase of SUPI, some items have lower support than SUPI, and the number of frequent items and the number of FT_Candidate are reduced. Thus reducing the mining time.
The following is the study of the running state of the algorithm in the dense dataset. Figure 4 and Figure 5 respectively show the running time in the dense dataset.

Figure 2. Processing time with SUP=1% and SUPI/SUP = 0.5 to 1 in sparse database
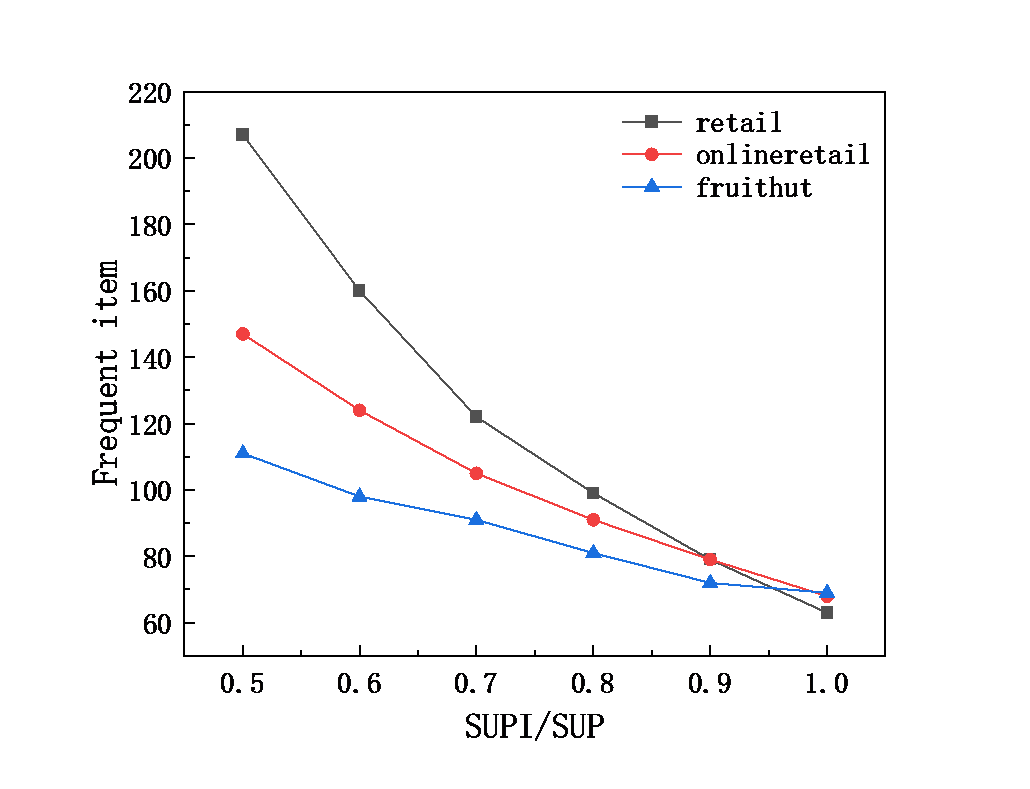
Figure 3. Frequent item with SUP=1% and SUPI/SUP = 0.5 to 1 in sparse database.
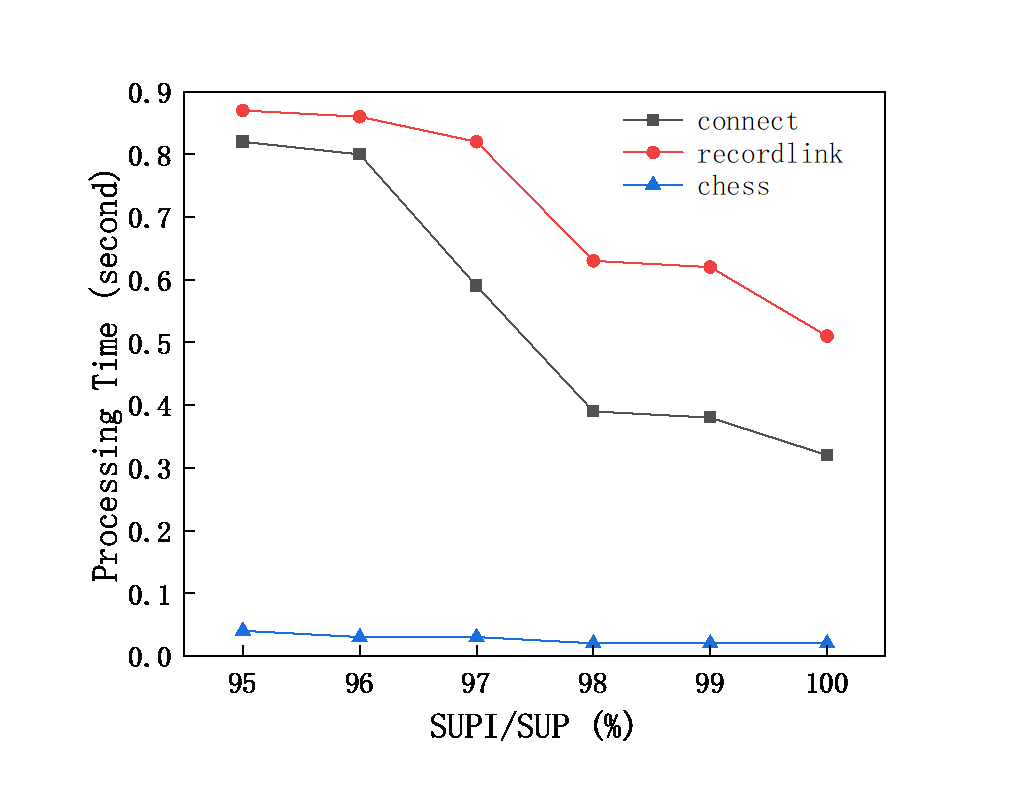
Figure 4. Processing time with SUP= 99% and SUPI/SUP=0.95 to 1 in dense database.
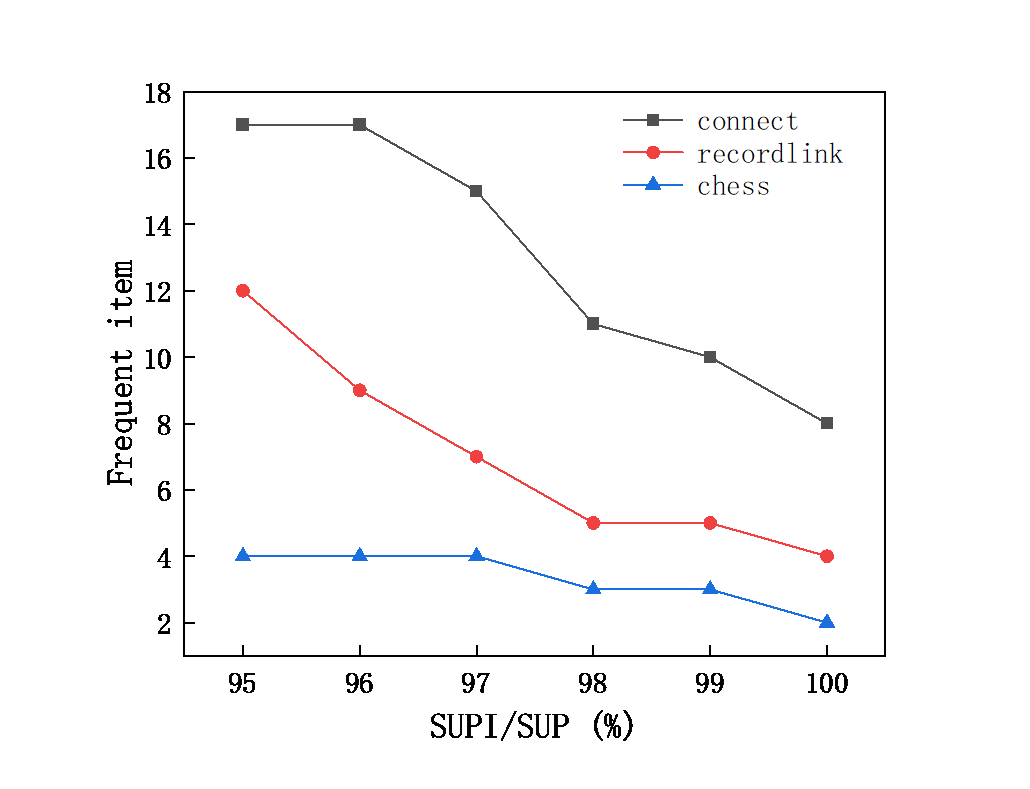
Figure 5. Frequent item with SUP=99% and SUPI/SUP = 0.95 to 1 in dense database.
As can be seen from Figure 4 and Figure 5, the number of frequent items and mining time decrease with the increase of support threshold gradually.
6. Conclusion
In this paper, based on the precise frequent item set mining algorithm, the algorithm gets the FT_Candidate by concatenating 1 in the binary with the generated FT_Pattern. It selects the corresponding horizontal chain according to the highest bit and the second highest bit of the binary number of the FT_Candidate and then carries out mining.
References
[1]. W. Ertel, Machine Learning and Data Mining, Income Introduction to Artificial Intelligence, W. Ertel, editor, Income Undergraduate Topics in Computer Science. , , London: Springer, 2011, pp. 161-220. London: Springer, 2011, pp. 161-220. doi: 10.1007/978-0-85729-299-5_8.
[2]. M. Cafaro and M. Pulimeno, Frequent Itemset Mining, Income Business and Consumer Analytics: New Ideas, P. Moscato and N. J. de Vries, editors, Cham: Springer International Publishing, 2019, pp. 269-304. doi: 10.1007/978-3-030-06222-4_6.
[3]. P. Fournier-Viger, J. C.-W. Lin, B. Vo, T. T. Chi, J. Zhang and H. B. Le, “A survey of itemset mining”, WIREs Data Mining and Knowledge Discovery, vol. 7, issue 4, July 2017 , doi: 10.1002/widm.1207.
[4]. F. M. Nafie Ali and A. A. Mohamed Hamed, “Usage Apriori and clustering algorithms in WEKA tools to mining dataset of traffic accidents”, Journal of Information and Telecommunication, Volume 2, Issue 3, Pages 231-245, July 2018, doi: 10.1080/24751839.2018.1448205.
[5]. S. Liu and C. K. Poon, “On Mining Proportional Fault-Tolerant Frequent Itemsets”, in Database Systems for Advanced Applications, vol. 8421, S. S. Bhowmick, C. E. Dyreson, C. S. Jensen, M. L. Lee, A. Muliantara, and B. Thalheim, editors, Income Lecture Notes in Computer Science, vol. 8421. , Cham: Springer International Publishing, 2014, pp. 342-356. doi: 10.1007/978-3-319-05810-8_23.
[6]. B. C. Hidayanto, R. F. Muhammad, R. P. Kusumawardani and A. Syafaat, “Network Intrusion Detection Systems Analysis using Frequent Item Set Mining Algorithm FP-Max and Apriori”, Procedia Computer Science, vol. 124, pp. 751-758, January 2017, doi: 10.1016/j.procs.2017.12.214.
[7]. X. Yu, H. Wang, X. Zheng and S. Liu, “A Model of Mining Noise-Tolerant Frequent Itemset in Transactional Databases”, in Proceedings 2015 International Conference on Intelligent Networking and Collaborative Systems, Taipei: IEEE, September 2015, pp. 21-24. doi: 10.1109/INCoS.2015.87.
[8]. J.-L. Koh and P.-W. Yo, “An Efficient Approach for Mining Fault-Tolerant Frequent Patterns Based on Bit Vector Representations”, in Database Systems for Advanced Applications, vol. 3453, L. Zhou, B. C. Ooi and X. Meng, editors, in Lecture Notes in Computer Science, vol. 3453, Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 568-575. doi: 10.1007/11408079_51.
[9]. S. Bashir, Z. Halim and A. Rauf Baig, “Mining fault tolerant frequent patterns using pattern growth approach”, In Proceedings 2008 IEEE/ACS International Conference on Computer Systems and Applications, March 2008, pp. 172-179. doi: 10.1109/AICCSA.2008.4493532.
[10]. S. Liu and C. K. Poon, “On mining approximate and exact fault-tolerant frequent itemsets”, Knowl Inf Syst, vol. 55, no. 2, pp. 361-391, May 2018, doi:. 10.1007/s10115-017-1079-4.
[11]. S. M. A. Ashraf and T. Nafis, “Fault Tolerant Frequent patterns mining in large datasets having certain and uncertain records”, p. 14.
[12]. Z. Li, F. Chen, J. Wu, Z. Liu and W. Liu, “Efficient weighted probabilistic frequent itemset mining in uncertain databases”, Expert Systems, vol. 38, no. 5, pp. e12551, 2021, doi: 10.1111/exsy.12551.
[13]. G. Lee, S.-L. Peng and Y.-T. Lin, “Proportional fault-tolerant data mining with applications to bioinformatics”, Inf Syst Front, vol. 11, no. 4, pp. 461-469, September 2009, doi: 10.1007/s10796-009-9158-z. -469, September 2009, doi: 10.1007/s10796-009-9158-z.
Cite this article
Li,X.;Lu,J. (2024). FT_HTlist: A fault-tolerant frequent itemset mining algorithm based on the linear table. Theoretical and Natural Science,34,72-76.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Computing Innovation and Applied Physics
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. W. Ertel, Machine Learning and Data Mining, Income Introduction to Artificial Intelligence, W. Ertel, editor, Income Undergraduate Topics in Computer Science. , , London: Springer, 2011, pp. 161-220. London: Springer, 2011, pp. 161-220. doi: 10.1007/978-0-85729-299-5_8.
[2]. M. Cafaro and M. Pulimeno, Frequent Itemset Mining, Income Business and Consumer Analytics: New Ideas, P. Moscato and N. J. de Vries, editors, Cham: Springer International Publishing, 2019, pp. 269-304. doi: 10.1007/978-3-030-06222-4_6.
[3]. P. Fournier-Viger, J. C.-W. Lin, B. Vo, T. T. Chi, J. Zhang and H. B. Le, “A survey of itemset mining”, WIREs Data Mining and Knowledge Discovery, vol. 7, issue 4, July 2017 , doi: 10.1002/widm.1207.
[4]. F. M. Nafie Ali and A. A. Mohamed Hamed, “Usage Apriori and clustering algorithms in WEKA tools to mining dataset of traffic accidents”, Journal of Information and Telecommunication, Volume 2, Issue 3, Pages 231-245, July 2018, doi: 10.1080/24751839.2018.1448205.
[5]. S. Liu and C. K. Poon, “On Mining Proportional Fault-Tolerant Frequent Itemsets”, in Database Systems for Advanced Applications, vol. 8421, S. S. Bhowmick, C. E. Dyreson, C. S. Jensen, M. L. Lee, A. Muliantara, and B. Thalheim, editors, Income Lecture Notes in Computer Science, vol. 8421. , Cham: Springer International Publishing, 2014, pp. 342-356. doi: 10.1007/978-3-319-05810-8_23.
[6]. B. C. Hidayanto, R. F. Muhammad, R. P. Kusumawardani and A. Syafaat, “Network Intrusion Detection Systems Analysis using Frequent Item Set Mining Algorithm FP-Max and Apriori”, Procedia Computer Science, vol. 124, pp. 751-758, January 2017, doi: 10.1016/j.procs.2017.12.214.
[7]. X. Yu, H. Wang, X. Zheng and S. Liu, “A Model of Mining Noise-Tolerant Frequent Itemset in Transactional Databases”, in Proceedings 2015 International Conference on Intelligent Networking and Collaborative Systems, Taipei: IEEE, September 2015, pp. 21-24. doi: 10.1109/INCoS.2015.87.
[8]. J.-L. Koh and P.-W. Yo, “An Efficient Approach for Mining Fault-Tolerant Frequent Patterns Based on Bit Vector Representations”, in Database Systems for Advanced Applications, vol. 3453, L. Zhou, B. C. Ooi and X. Meng, editors, in Lecture Notes in Computer Science, vol. 3453, Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 568-575. doi: 10.1007/11408079_51.
[9]. S. Bashir, Z. Halim and A. Rauf Baig, “Mining fault tolerant frequent patterns using pattern growth approach”, In Proceedings 2008 IEEE/ACS International Conference on Computer Systems and Applications, March 2008, pp. 172-179. doi: 10.1109/AICCSA.2008.4493532.
[10]. S. Liu and C. K. Poon, “On mining approximate and exact fault-tolerant frequent itemsets”, Knowl Inf Syst, vol. 55, no. 2, pp. 361-391, May 2018, doi:. 10.1007/s10115-017-1079-4.
[11]. S. M. A. Ashraf and T. Nafis, “Fault Tolerant Frequent patterns mining in large datasets having certain and uncertain records”, p. 14.
[12]. Z. Li, F. Chen, J. Wu, Z. Liu and W. Liu, “Efficient weighted probabilistic frequent itemset mining in uncertain databases”, Expert Systems, vol. 38, no. 5, pp. e12551, 2021, doi: 10.1111/exsy.12551.
[13]. G. Lee, S.-L. Peng and Y.-T. Lin, “Proportional fault-tolerant data mining with applications to bioinformatics”, Inf Syst Front, vol. 11, no. 4, pp. 461-469, September 2009, doi: 10.1007/s10796-009-9158-z. -469, September 2009, doi: 10.1007/s10796-009-9158-z.









