1. Introduction

Fourier Analysis, named after the French mathematician Jean-Baptiste Joseph Fourier, is a mathematical technique that transforms a function of time, space, or any other variable into a function of frequency. It decomposes complex waveforms into simpler components, specifically into sines and cosines, which are easier to analyze and understand. This transformation is pivotal in numerous fields, including engineering, physics, and, notably, music analysis [1-3].

The relevance of Fourier Analysis to music stems from its ability to dissect musical tones into their constituent frequencies, offering a deep dive into the acoustic properties that define the unique sound, or timbre, of musical instruments [4]. In music theory and acoustics, the application of Fourier Analysis transcends basic tone analysis. It plays a crucial role in digital signal processing, enabling technologies such as MP3 compression, noise reduction, and the synthesis of musical sounds [5]. For musicians and sound engineers, Fourier Analysis provides a scientific basis for crafting sounds and understanding their interaction in compositions and recordings. It bridges the gap between the physics of sound production and the perception of music, offering insights into the construction of musical instruments and the development of electronic sound synthesis and audio processing tools. Chen studied the interaction between music and vision based on Fourier transform, providing a visualization method that can be used in musicology related research and interactive media creation methods [6]. By performing Fourier transform on the audio of different instruments and analyzing the distribution of harmony between instruments, the characteristics of each style were presented by Yuan [7]. Xu used discrete Fourier transform to study the composition principle of musical notes on the original signal, and used inverse discrete Fourier transform to generate music [8].

This paper will analyze musical tones, specifically focusing on recordings from a trumpet, piano, and flute. The primary objective is to utilize Fourier Analysis, via MATLAB, to dissect and compare the unique frequency signatures of these instruments. The methodology spans data collection, preprocessing, application of Fourier Transform, and subsequent analysis.

2. Applications of Fourier Transformation

The applications of Fourier Transformation to the audio samples of the trumpet, piano, flute, piano and triangle reveals intricate details about the acoustic properties that differentiate these instruments. Utilizing MATLAB for the analysis, this section discusses the findings from the frequency domain perspective, providing insights into the unique sonic signatures of each instrument.

2.1. Musical Instruments: Fundamental Frequencies and Harmonics

The Fourier Transform of each instrument’s audio recordings illuminated the presence of fundamental frequencies corresponding to the played notes, alongside multiple harmonics that contribute to the timbre or color of the sound.

The trumpet recordings showcased a strong fundamental frequency with a series of harmonics that decayed less rapidly than those of the piano and flute in Figure 1. This characteristic brass “brightness” is due to the trumpet’s ability to produce strong higher-order harmonics.

Figure 1. Time domain signal and frequency domain signal for the trumpet

Piano samples displayed a complex harmonic structure with a rich set of overtones in Figure 2. The decay of these harmonics was more pronounced, contributing to the piano’s distinct reverberation and tonal complexity.

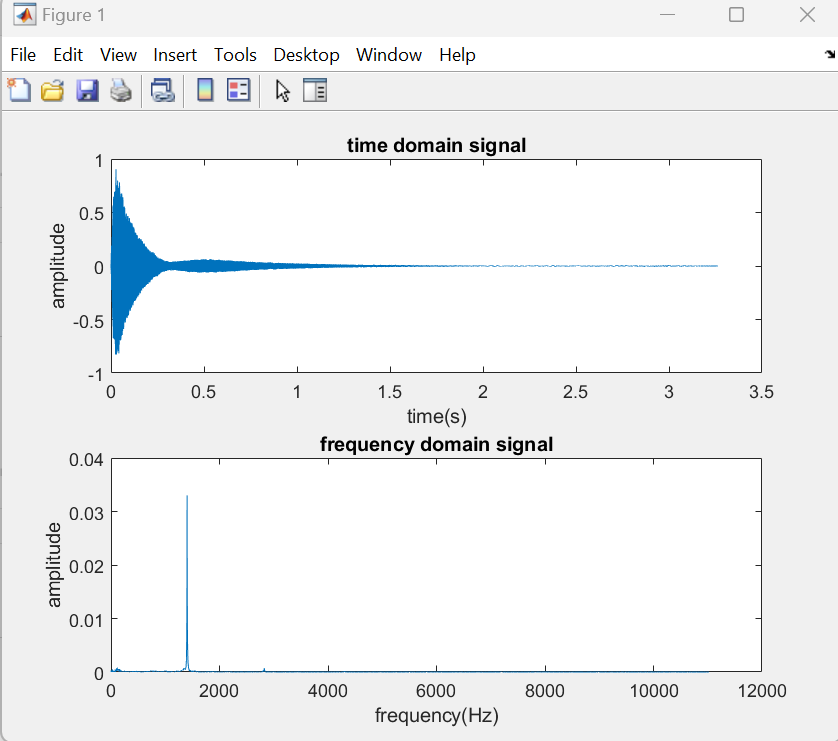
Figure 2. Time domain signal and frequency domain signal for the Piano

The flute’s frequency spectrum was simpler, with a clear fundamental frequency and fewer harmonics in Figure 3. The flute’s sound is purer and more sine-wave-like, owing to the instrument’s acoustical properties, which favor the fundamental frequency over the harmonics.

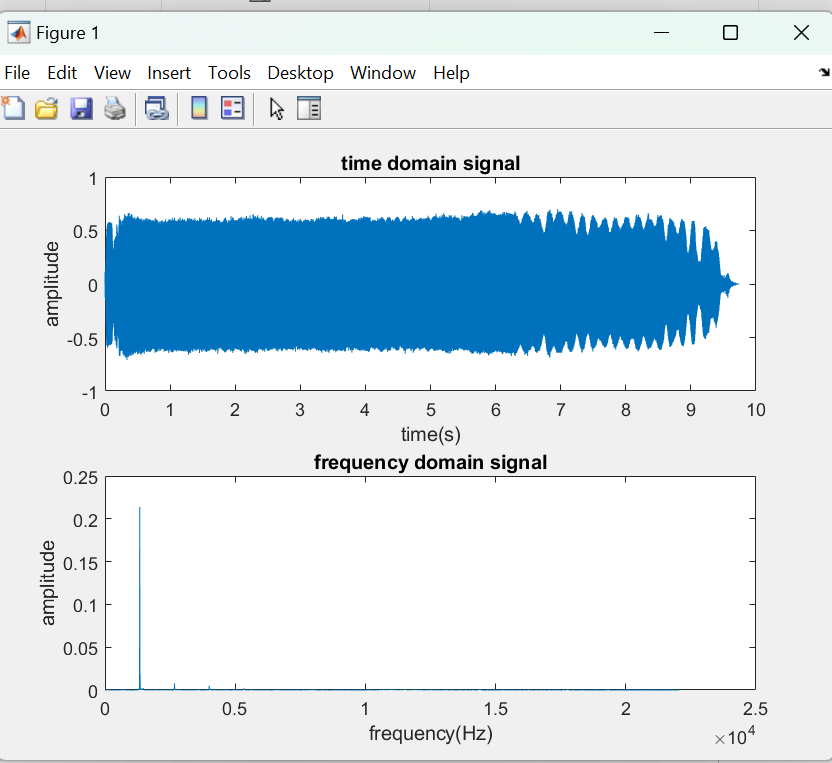
Figure 3. Time domain signal and frequency domain signal for the flute

The visualizations produced in MATLAB effectively highlighted the differences in harmonic content among the instruments. Plots of magnitude against frequency for each instrument at various notes provided a visual representation of the acoustic fingerprints. These plots were instrumental in identifying the unique patterns of harmonics that define the sound of each instrument.

2.2. Noise Instruments

This Other instruments like drums and triangles that don’t have a clear fundamental frequency are noise instruments.

For drums, which produce rich and complex sounds with a broad spectrum of frequencies due to their diverse modes of vibration, the Fourier Transform can decompose these sounds into their constituent frequencies in Figure 4. This decomposition helps in understanding the timbral qualities of the drum, revealing how different materials, shapes, and sizes affect the sound’s frequency content. By analyzing the spectral content, sound engineers and instrument makers can modify and optimize drum designs to achieve desired sound qualities, from the deep, resonant bass of a kick drum to the sharp, concise attack of a snare.

Similarly, the triangle, despite its seemingly simple structure, produces a sound rich in overtones. The Fourier Transform can uncover this intricate harmonic structure, showing a spectrum dense with harmonics that contribute to its bright, penetrating quality. This analysis not only aids in the crafting of triangles with specific tonal characteristics but also in digital synthesis and sampling, where understanding the spectral content is crucial for recreating realistic triangle sounds in in Figure 5.

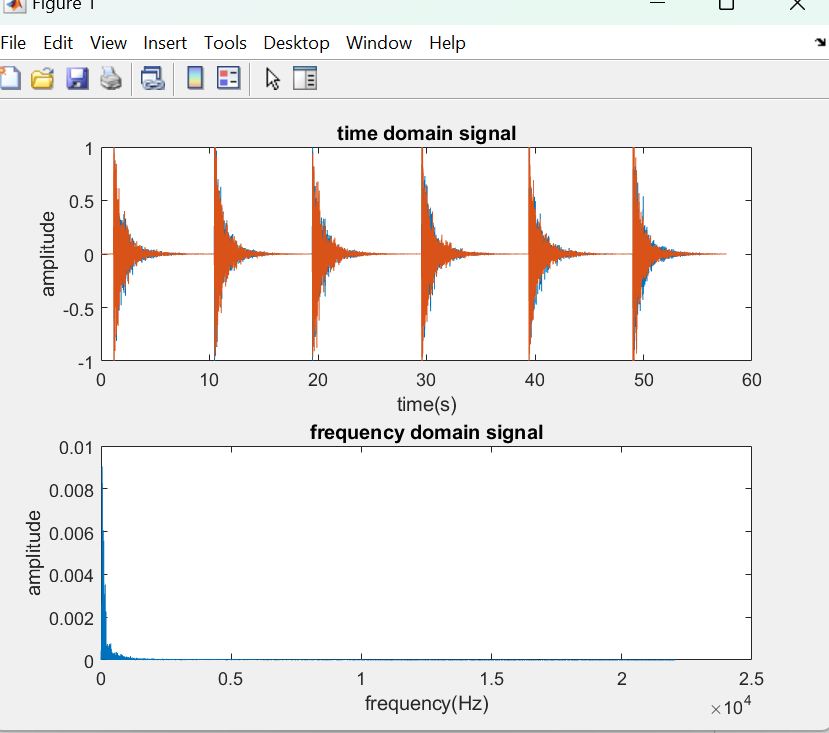
Figure 4. Time domain signal and frequency domain signal for the drum

2.3. Implications

The implications of this research extend far beyond academic inquiry, touching upon several practical and theoretical aspects of music and sound engineering.

Understanding the frequency makeup of instruments can enhance teaching methods, providing students with a more nuanced appreciation of music composition and instrument design. Insights into the harmonic content and how it contributes to timbre can inform the design of new instruments or the refinement of existing ones, aiming to achieve desired sound qualities. The principles uncovered through Fourier Analysis are directly applicable in the development of audio processing software, including effects, synthesis, and noise reduction algorithms. Producers and sound engineers can leverage this knowledge to manipulate recordings more effectively, ensuring that the desired emotional and aesthetic impacts of music are achieved.

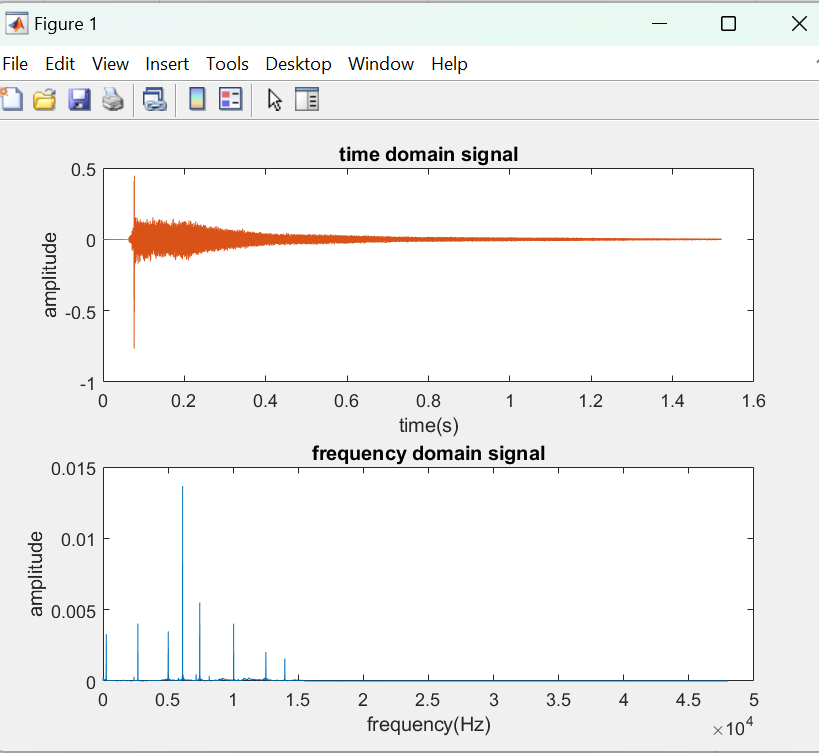
Figure 5. Time domain signal and frequency domain signal for the triangle

3. Conclusion

The exploration of musical tones through Fourier Transformation has yielded significant insights into the unique acoustic characteristics of the trumpet, piano, and flute. This analytical journey, underpinned by mathematical rigor and facilitated by MATLAB, has illuminated the complex interplay between fundamental frequencies, harmonics, and the resultant timbre of musical instruments. By dissecting sound into its constituent frequencies, Fourier Analysis has provided a quantifiable understanding of what gives each instrument its distinctive sound.

This study represents a step towards demystifying the complex relationship between the physics of sound production and the perceived qualities of musical tones. The application of Fourier Transformation offers a powerful lens through which to view the intricacies of music, providing a foundation for future research and innovation in music theory, acoustics, and digital audio technology. With the development of technology, the potential for new discoveries and applications in the realm of music and sound engineering will be vast.