1. Introduction

The Department of Finance and risk management has made great progress as the framework of theory and the promotion of technological innovation. It is intended to identify, analyze and mitigate the negative impact of market uncertainty in financial portfolios. This paper examines the basic aspects of methodological underlying probability and statistical analysis to quantify potential losses and assess the effectiveness of risk mitigation strategies. This paper discusses the role of probability distribution in loss modeling and the application of statistical models to predict future market trends. As the explanation progresses, we will explore the complex process of model calibration, optimization and verification. These steps are important to ensure the accuracy and reliability of risk management models that must correspond to dynamic market conditions. In the discussion, the importance of data collection and preprocessing is emphasized, and it is pointed out that the data structure should be organized, structured and constructed for analysis purposes. In addition, the document examines various risk mitigation measures, including the multilevel of assets, compliance and capital adequacy. These strategies are important to prevent financial system stability and potential crises. In addition to the conventional risk management techniques, we examine the critical impact of advanced technologies such as machine learning and block chains [1]. These innovations provide new ways to improve the accuracy and efficiency of risk management practices, provide real-time information, and automate the compliance process. This paper summarizes these arguments and claims the adoption of a comprehensive financial risk management technique that combines traditional theoretical models and advanced technical solutions. This approach is important to overcome the complexity of modern financial environments and ensure the flexibility and stability of financial institutions.

2. Theoretical Framework

2.1. Foundations of Probability in Risk Management

Probability theory is a pillar of financial risk management and provides a structured approach to quantifying the potential adverse effects of uncertainty and financial portfolios. Such quantization involves various probability distributions (e.g., normal distribution, lognormal distribution, Poisson distribution) to model potential losses in various financial institutions and markets. For example, the normal distribution assumes that the future price of the asset follows the logarithmic distribution, and is widely used in the black shovel option price model which reflects the asymmetry of the asset price and its higher price, as shown in Figure 1. Applying these distributions can calculate the expected loss and evaluate extreme risk [2]. This is important to determine the capital reserves needed to cover potential losses. In addition, the probability model enables the evaluation of the effectiveness of risk mitigation strategies by simulating the impact of diversification, hedging and insurance on portfolio loss allocation. Advanced technologies such as copula models are used to understand the dependent structure between different financial institutions to more accurately model common extreme risks. These models are components that make up a comprehensive risk management framework corresponding to the complexity of financial markets.

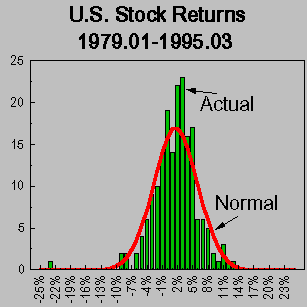
Figure 1. Comparison of Actual U.S. Stock Returns to Normal Distribution (1979-1995) (Source: people.duke.edu)

2.2. Statistical risk analysis

Statistical analysis plays a central role in measuring and managing financial risks to predict future market trends and variability using past data. For example, it is used to identify factors that have a major impact on the performance of financial assets and to estimate the return of assets from those factors. A time series prediction model, such as autoregressive integrated moving average (ARIMA) and wide range generalized autoregressive conditional heteroskedasticity (GARCH), is used to predict future volatility from past patterns of variability and to know potential changes in the market. In contrast, Monte Carlo simulation provides a robust way to evaluate the impact of different scenarios on portfolio performance by generating a large amount of potential for future market conditions based on statistical attributes derived from past data. This approach is particularly useful in calculating the expected maximum loss risk (VaR) and conditional risk value (CVaR) in a particular period of time at a particular level of confidence:

\( {VaR_{α}}=-(μ+{z_{α}}×{σ_{t}}) \) (1)

Where μ is the expected return (which could be forecasted using an ARIMA model). \( {z_{α}} \) is the α-quantile of the standard normal distribution (for a 95% confidence level, z_0.05 is typically 1.645). \( {σ_{t}} \) is the standard deviation of returns (volatility) at time t forecasted using a GARCH model [3].

By incorporating empirical data into a risk model, statistical analysis identifies important risk factors and enhances the accuracy of the model in anticipating future events and realizes a more effective risk mitigation strategy.

2.3. Mathematical evaluation of risk assessment

The combination of probability and statistical analysis led to the construction of a precise mathematical model for assessing financial risk. Var (risk value) and CVaR (conditional risk value) are two important models in this field. Var measures the maximum loss that the portfolio can receive during a given period of time in the normal market conditions at the given confidence level. On the other hand, CVaR provides an expected loss estimation over the threshold of VaR and provides a more comprehensive view of extreme risk. These models integrate the distribution of earnings and allow the measurement of the openness of the risk quantitatively considering the asymmetry and flatness of the characteristics of financial data. For example, the VAR model can be implemented using a distributed covariance approach that simplifies the historical simulation technique that uses past benefits directly to estimate future potential losses and the calculation of VaR, but assumes that the revenue that may underestimate the extreme loss risk is a normal distribution [4]. The calculation of CVaR is often followed by Monte Carlo simulation, and the amount of calculation is enormous, but by considering the nonlinearity and asymmetry of the financial equipment, the situation of the risk can be reflected more accurately. These models are not without criticism. Especially, it is about the hypothesis of the market condition, the correlation between the past data and the future risk. But they are still the basic tools in the financial risk management Arsenal and lead the work of strategic decision and compliance supervision. By using these models, the agency can better assess the range of various financial risks and promote the practice of wisely and strategic risk mitigation.

3. Model Implementation and Validation

3.1. Data collection and preprocessing

The creation of an effective financial risk management model begins with data collection and detailed preprocessing. This is an important step to lay foundations for all subsequent modeling tasks. In the collection phase, aggregates information from various data sources such as financial statements, market trends, credit reports, transaction logs. Preprocessing these data is very important to ensure that it is suitable for statistical analysis and requires complex procedures. First, data cleanup is done to identify and correct all errors and disagreements, such as missing or abnormal values that may affect the integrity of the analysis. Next, we use the standardized technology to scale digital data so that different variables can contribute to analysis equally. The structuring process is a process of converting unstructured data and semi structured data into a form suitable for statistical analysis, including converting metric text data into quantifiable metrics. Finally, we use feature engineering to create new variables that can predict the risk model better [5]. This requires deep understanding of that field to find relevant predictors. Maintaining the integrity of data at all stages will comply with strict legal and ethical standards to ensure privacy and security of data.

3.2. Model calibration and optimization.

Calibration and optimization of risk models are important steps to ensure their effectiveness and reliability. Calibration focuses on improving model performance by identifying model parameters to model model output to match past data, and optimizing the optimal parameter set to minimize prediction errors. This requires applying various techniques, such as grid search for integrated parameter search, random search for more efficient parameter samples, gradient drop for iterated parameter adjustment aiming at minimizing predefined loss functions. In parallel with these optimization techniques, there are cross validation techniques. Cross validation technology evaluates model performance on unseen data and avoids overfitting [6]. This stage is important to greatly affect the accuracy of the prediction and the reliability of the model, to select the appropriate algorithm and to adjust the hyperparameters. Table 1 summarizes various techniques used in the calibration and optimization of risk models.

Table 1. Overview of Model Calibration and Optimization Techniques in Financial Risk Management

3.3. Model Testing and Validation

The final stage of implementation, testing and verification of risk models is important to ensure the robustness and reliability of financial risk models. This complete flow starts with a back test and the model evaluates the accuracy of the prediction based on the time data. The model then undergoes stress tests tested in extreme but reliable scenarios to assess resiliency and identify potential weaknesses in difficult market conditions. We evaluate the performance of the model using accuracy, accuracy, recall rate, F1 score and the bottom product of the ROC curve of the classification model, the square mean error of the regression model, the square mean error, the R square error, and so on. At this stage, cross validation is performed to ensure that the model is valid for invisible data, reducing the risk of overfitting. This stage is important for repetitive tuning of the model, and incorporates feedback and verification feedback in other optimization periods to ensure that the model works not only in optimal ways but also for the regulatory and ethical considerations in financial risk management.

4. Risk mitigation measures

4.1. Asset diversification and insurance coverage

Multipurpose is to diversify investment into a wide class of assets and to minimize the impact of a single asset’s performance on the entire portfolio. Although the basic theory of diversification is rooted in the correlation of the return ratio of assets, it shows that there is zero correlation coefficient in the case of a fully diversified portfolio and there is no correlation between the performance of the two assets. This strategy is supported by MPT (investor portfolio theory) that allows investors to optimize their portfolio by balancing risk and return. Hedging uses options such as futures contracts and swaps to compensate for potential investment losses. One of the common hedging strategies is to use the option to avoid falling stock prices. This includes buying the right to sell certain securities at a given price to set the floor price for investors to receive additional losses. The cost of this insurance corresponds to premium to pay for options, and the premium may be rational by reducing the risk [7].

In practice, diversity and hedging implementation require strict quantitative analysis. Portfolio optimization models such as average variance optimization can be used to find portfolios that minimize risk at given expected revenue levels. Meanwhile, the black scool model provides an optional price mathematical framework for determining fair hedging costs. These mathematical models are essential to build a robust risk management framework that systematically mitigates the effects of market disadvantage.

4.2. Compliance regulation and sufficient capital

Careful supervision and capital adequacy are crucial to ensure the stability of financial systems. The Basel treaties demanded the lack of disclosure in the 2008 global financial crisis for the wealth and risk management of banks’ capital against them, and stricter. The primary capital and the concept of secondary capital are introduced, and primary capital includes major capital such as common stock and undistributed profit, and secondary capital includes supplementary capital such as undisclosed reserves and secondary long-term debt. The important aspect of Basel III is leverage and liquidity coverage (LCR). Leverage is a simple measure of bank capital and its magnitude and is intended to limit the level of debt that banks can borrow. On the other hand, LCR is calling for banks to hold enough high-quality current assets to pay cash outflows for 30 days. To protect these regulations, banks are accurately evaluating capital demand using different quantitative models [8]. The calculation of risk weighted assets (RWA) is very important in determining the minimum capital requirements. This is to assign the weight of the risk to the risk of each asset class, and the high-risk assets require more capital. An IRB based advanced approach allows banks to use the risk estimates of their own credit risk (carefully verified) and provide a more sensitive capital requirement assessment. Figure 2 represents a bank’s capital structure and the distribution of Risk Weighted Assets (RWA) by asset class.

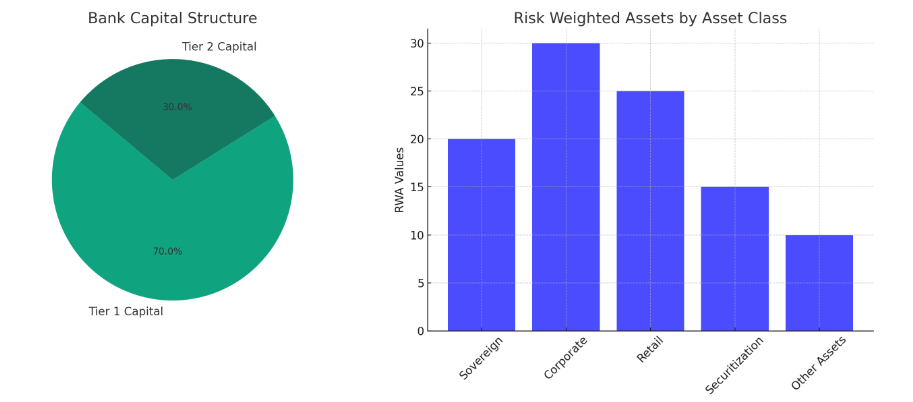
Figure 2. Bank Capital Composition and Risk-Weighted Asset Distribution under Basel III Standards

4.3. Advanced risk management technology

Integration of machine learning and block chain technology in financial risk management is a new innovation. Machine learning models such as neural networks and decision trees are increasingly adopted because they have an ability to analyze large data sets and identify complex nonlinear patterns of market behavior. These models take advantage of past data and respond to new information so that they can significantly improve credit default, market volatility and operational risk. Block chain technology provides a breakthrough solution to the transparency and wrongful problem of financial transactions using a distributed untamed ledger. Smart contracts can be used to automate compliance and risk management because contracts are automatically executed and the terms in the contract are written directly to the code. The smart contract can be dealt only when certain conditions are met, so the default chances are very low, reducing counter party risk. In addition, by applying a block chain to the creation of a trading logbook, the need for intermediation is reduced, and the transaction cost is lowered and the efficiency of financial markets is improved. The potential to increase the accuracy and effectiveness of risk data through real-time reporting and verification processes may fundamentally alter the practice of risk management.

In this way, the diversification of specific strategies, compliance with regulatory frameworks such as Basel III, the adoption of advanced technologies such as machine learning and block chains are changing the way of managing financial risk. These methods not only reduce the risk but also help the overall stability and toughness of the financial system.

5. Conclusion

The structure of financial risk management has witnessed the paradigm shift and its driving force is in the progress of theory and the integration of innovative technologies. This paper explores the principles behind financial risk management, including the application of probability and statistical analysis, development and verification of risk models, and implementation of effective risk mitigation strategies. This comprehensive review emphasizes the importance of maintaining the integrity of the data, optimizing the performance of the model, and adhering to the supervision criteria to ensure the robustness and reliability of financial risk management practices. In addition, the advent of machine learning and block chain technology has prevailed in the new era of financial risk management and has unprecedented opportunities for improving the accuracy and efficiency of risk assessment and relaxation processes. By adopting these technologies, the financial desk will not only be able to control the financial market more effectively, but also increase the stability and toughness of the entire financial system.

Thus, an integrated approach combining traditional risk management techniques and innovations shows an example of the future of financial risk management. This balanced approach is crucial for wisely strategic decisions, supervisory management, and the promotion of careful and strategic risk mitigation throughout the financial sector.