1 Introduction

Yang-Mills theory stands as a central pillar in our understanding of fundamental interactions, providing a unifying language for the electromagnetic, weak, and strong forces within the framework of quantum field theory. The seminal work of Chen-Ning Yang and Robert Mills extended the concept of local gauge invariance from the abelian group associated with electromagnetism to non-abelian gauge groups, laying the foundation for the development of quantum chromodynamics and the electroweak theory. This generalization has since played a pivotal role in the formulation of the Standard Model of particle physics.

The mathematical richness of Yang-Mills theory is encapsulated by its deep connection with differential geometry, particularly through the study of connections on principal bundles and the associated curvature forms. This paper aims to present a comprehensive examination of the interplay between Yang-Mills theory and differential geometry, with a focus on the self-duality of solutions to the Yang-Mills equations and their geometric significance.

We begin by revisiting the fundamental aspects of the study of self-duality, showcasing its role as a special solution to the Yang-Mills equations and its implications for the geometry of four-dimensional manifolds.

A key component of our discussion is the introduction of twistor theory, originally developed by Roger Penrose as a novel approach to encoding geometric and algebraic properties of spacetime. By bringing complex algebraic geometry into play, twistor theory offers an elegant method for addressing non-linear differential equations related to self-duality, enriching both mathematical and physical perspectives on space-time.

Building on the foundational work of Atiyah, Hitchin, and Singer [1], we explore the relationship between self-dual Yang-Mills fields and holomorphic complex structures. Their insights into the application of twistor theory to self-dual Yang-Mills fields have unveiled a remarkable correspondence with holomorphic structures, a correspondence that remains a vibrant area of research.

The final part of the paper is dedicated to the study of cohesive modules over four-dimensional manifolds. By leveraging the profound connections established by Atiyah between self-dual Yang-Mills fields and holomorphic fields, we extend the classical framework to the realm of cohesive modules. This extension not only provides new insights into the correspondence between self-dual Yang-Mills fields and holomorphic vector bundles but also opens up the possibility of exploring further relationships between their categories.

2 Self-duality in Four Dimensional manifolds

The concept of self-duality holds significant sway in both the realms of mathematics and physics, representing a symmetry that often leads to deep insights and results. In the context of this research, we confine our discussion to self-duality within the framework of four-dimensional spaces, where the Hodge star operator \( * \) satisfies the condition \( *^{2}=1 \) . This specific dimensional setting is particularly notable in fields such as the study of four-manifolds, and it plays a crucial role in the formulation of theories such as topological quantum field theory and the gauge theory of the Yang-Mills equations.

2.1 Self-duality and Anti Self-duality

Hodge star \( * \) is the conceptual principle in self-duality we are going to talk about. It was used in electron-magneticism where it arises in the coordinate-free formulation of Maxwell’s equations in flat space time. It is an operator that provides duality between \( k \) -forms and \( (n-k) \) -forms in \( R^{n} \) .

Definition 2.1 (Hodge Star). [5] Let \( w=dx_{i_{1}}∧...∧dx_{i_{k}} \) be a basic \( k \) -form in \( R^{n} \) . Then the Hodge star dual of \( w \) , which is denoted by \( *w \) , is the unique basic \( (n-k) \) -form with the property:

\( w∧*w=dx_{1}∧...∧dx_{n} \)

For general \( k \) -forms on \( U∈R^{n} \) , we extend the Hodge star by linearity: If

\( η=\sum_{1}^{k} f_{i_{1}}..._{i_{k}}dx_{i}∧...∧dx_{i_{k}} \)

is a k-form on set \( U \) , then its Hodge star dual \( *η \) is the \( (n-k) \) -form given by

\( *η=\sum_{1}^{k} f_{i_{1}}..._{i_{k}}*dx_{i}∧...∧dx_{i_{k}} \)

Definition 2.2 (Self-duality). Let \( F \) be a 2-form, we say it is self-dual (resp. anti self-dual) if \( *F=F \) (resp. \( *F=-F \) ). This is when \( *^{2}=I \) and that when it is \( Λ^{+} \) , then \( *F=F \) and when \( Λ^{-} \) , then \( *F=-F \) .

Now, with the knowledge of self-duality, let’s revisit the concept of Einstein manifold.

Proposition 2.3 ([1]). A 4-manifold \( M^{4} \) is Einstein if and only if the Levi-Civita connection on \( Λ^{+} \) is self-dual.

Proof. The curvature of \( Λ^{+} \) is given by the first row of block decomposition of the curvature tensor. Therefore, the anti-self-dual part \( B^{*} \) doesn’t appear iff \( M \) is an Einstein manifold.

2.2 Yang-Mills Theory

Yang-Mills theory represents a quantum field theoretical extension of classical Maxwell’s electromagnetism, providing a sophisticated framework for understanding electromagnetic fields and forces with remarkable precision. As a non-abelian gauge theory, it is instrumental in modeling the weak and strong nuclear interactions, which, in their unadulterated theoretical form, feature massless gauge bosons—a characteristic that poses challenges for reconciling the theory with observable phenomena in the physical world. This conundrum remains one of the outstanding problems in theoretical physics.

The foundations of Yang-Mills theory are deeply rooted in group theory, drawing specifically from the rich structure of Lie groups. In our exploration, we approach Yang-Mills theory through the lens of differential geometry, which offers a geometric perspective on the fields and interactions described by the theory.

To proceed, we must first introduce the concept of a Yang-Mills field, also commonly referred to as a gauge field. This entity encapsulates the dynamics of the gauge bosons and is a pivotal element in the geometric formulation of the interactions that govern the fundamental forces.

Definition 2.4 (Yang-Mills Field). Let \( π:P→M \) be a principal \( G \) -bundle over a Riemannian manifold \( M \) , and let \( E=P×_{G}E→M \) be the vector bundle associated with \( π \) and a \( G \) -module \( E \) . Connection on \( E \) is a differential operator

\( ∇^{E}:Γ(E)→Γ(T^{*}M)⨂Γ(E) \)

which acts on the space \( Γ(E) \) of sections of E(M). The operator \( d^{*} \) , on \( p \) -forms, conjugates to

\( d^{*}=(-1)^{d(p+1)+1}*d*. \)

The connection \( ∇ \) in a principal \( G \) -bundle is called a Yang-Mills field if the curvature \( ∇F \) satisfies \( dF=0 \) and \( d^{*}F=0 \) .

Lemma 2.5. We define

\( D^{*}:Ω^{p}(AdE)→Ω^{p-1}(AdE) \)

as the operator dual to

\( D:Ω^{p-1}(AdE)→Ω^{p}(AdE) \)

where \( Ad \) is the adjoint bundle, or the vector bundle corresponding to the principal. Then

\( D^{*}=(-1)^{d(p+1)+1}*(d+A)* \)

Proof. Since

\( **=(-1)^{p(d-p)} \)

where \( *:Ω^{p}(AdE)→Ω^{d-p}(AdE) \) operates on the differential form part and \( A_{i} \) and \( * \) commute as \( *A_{i}*=A_{i} \) . Thus, because \( A_{i} \) is skew symmetric and

\( D=d+A,A=Ω^{1}(AdE) \)

\( D^{*}=(-1)^{d(p+1)+1}*(d+A)*=(-1)^{d(p+1)+1}*D* \)

Lemma 2.6. (Anti) self-dual metric connection is a special solution to Yang-Mills equation.

Proof. The Yang-Mills equation is

\( D^{*}F=0. \)

By the previous lemma we proved, this implies

\( D*F=0. \)

Let F be (anti)self-dual, which is

\( F=±*F. \)

Then the Yang-Mills equation becomes

\( D**F=0 \)

Since \( **=Id \) ,

\( DF=0 \)

which is true because it is the Bianchi identity

\( ∇_{ρ}R_{μ}=\frac{1}{2}∇_{μ}R \)

where \( R_{m}u \) is the Ricci tensor, \( R \) is the scalar curvature, and \( ∇_{ρ} \) indicates covariant differentiation. Thus, we proved that every (anti) self-dual connection gives automatically a Yang-Mills connection.

3 Complex Structure and Twistor Space

Having delineated the definition of self-dual Yang-Mills equations and explored salient examples, we are now equipped to turn our attention to another central object of interest in this research—the almost complex structure. This geometric construct, pivotal to our discourse, enriches our understanding of the manifold’s structure by endowing it with a generalized notion of complex geometry, even in contexts where a true complex structure may not exist. We will examine the properties of almost complex structures and their interactions with the self-dual solutions of the Yang-Mills equations, thereby revealing the intricate interplay between geometry and physics that underpins the theoretical landscape of differential geometry.

3.1 Complex Structure

Definition 3.1 (Almost-complex Structure). Almost-complex structure on manifold \( X^{2n} \) is defined as

\( J:T_{x}M→T_{x}M,J^{2}=-Id. \)

With this, we can define almost-complex manifolds and complex manifolds.

Definition 3.2 (Complex Manifold). If \( U⊂C^{n} \) is open, and \( f:U→C \) , then \( f \) is holomorphic if it satisfies the Cauchy-Riemann equation \( \frac{∂Imf}{∂x_{i}}+\frac{∂Ref}{∂y_{i}}=0 \) . A complex manifold of (complex) dimension \( n \) , is a manifold of real dim \( 2n \) , with local coordinates \( z_{1},...,z_{a}:u→C \) .

3.2 Twistor Space

Twistor spaces are distinguished complex three-dimensional manifolds that establish a profound correspondence with specialized Riemannian geometries on four-dimensional manifolds. This remarkable relationship between complex three-dimensional manifolds and their real four-dimensional counterparts is encapsulated by the Penrose twistor correspondence, a foundational concept that bridges the gap between complex and Riemannian geometry.

Prior to delving into the construction of a twistor space over \( S^{3} \) , it is instructive to consider the well-known example of a sphere bundle, denoted \( S(M) \) , with the Torus serving as an illustrative case. This example will provide a concrete setting to appreciate the nature of sphere bundles and their relevance in the broader context of differential geometry, paving the way for a deeper exploration of twistor spaces and their applications.

Example 3.3. The Torus has the base manifold to be a circle, and the fibres are also circles, therefore, it is a sphere bundle expressed by \( S^{1}×S^{1} \) .

Example 3.4 (Mini-twistor Space). Let’s start from \( R^{2} \) , since we know the complex plane can be represented as \( z=x+iy \) and can thereby identify \( R^{2} \) with \( C \) . We discover a function \( f:R^{2}→R \) is harmonic if and only if we can write it as

\( f=ψ+\overline{ψ} \)

where \( ψ:C→C \) is a holomorphic function. In the above process, we have related real valued functions to holomorphic functions of one-variable.

However, we can’t apply this method to \( R^{3} \) because it has an odd dimension. We can still form another space that is closely associated to the geometry of \( R^{3} \) , and this space \( Z \) of all oriented lines of \( R^{3} \) is known as mini-twistor space. Since any oriented line \( l \) is uniquely determined by the unit vector \( u \) parallel to the line and the shortest vector \( u \) from the origin of and is orthogonal to the line, therefore we have

\( l=v+tu|t∈R. \)

Then we get

\( Z=(u,v)|u,v∈R^{3},∥u∥=1, \lt u,v \gt =0⊂S^{2}×R^{3}. \)

In conclusion, the mini-twistor space \( Z \) is readily seen to be \( TS^{2} \) which is the tangent bundle of two-sphere. In other words, the sum of all tangent planes of the two-sphere.

Now, we can create an analogue of mini-twistor space and define Twistor space in 4-dimensions.

Definition 3.5. Twistor Space Twistor space \( Z \) is the fibre bundle with manifold \( M \) as a base manifold, and all the almost complex structures on \( T_{x}M \) as fibres. As \( Z=S(λ^{-}) \) , \( J:T_{(x,y)}Z→T_{(x,y)}Z \) (where \( J=J_{1}⨁J_{2} \) , \( J_{1}:T_{x}M→T_{x}M \) and \( J_{2}:S_{x}^{2}→S_{x}^{2} \) .

The above definition is only one way to define the twistor space. It is also commonly defined using its identity with the open set of the 3-dimensional complex projective space \( CP^{3} \) : the space of all complex lines through the origin in \( C^{4} \) .

4 Cohesive Modules over Self-dual manifolds

Introduced by Block[3], cohesive modules have emerged as an influential concept for probing the dynamics of vector bundles and sheaves when subjected to deformations. These modules transcend the confines of the traditional holomorphic framework, opening avenues to investigate a wider spectrum of geometric contexts. Central to their utility is the insight they afford into the deformation theory of vector bundles and sheaves, shedding light on the nuanced aspects of their stability and responsiveness to perturbations.

Furthermore, cohesive modules provide an apt language for the formulation and exploration of moduli spaces. These spaces serve as a cataloging tool, systematically parameterizing families of geometric entities such as vector bundles or sheaves, distinguishing them up to isomorphism, and thus offering a means to classify and comprehend the vast terrain of geometric structures.

Situated within the expansive domain of higher categories and derived geometry, cohesive modules enhance our grasp of geometric intricacies, extending well beyond the realms traditionally captured by classical geometry.

In the ensuing section, we aim to broaden the scope of classical self-dual Yang-Mills fields through the incorporation of cohesive modules, thereby enriching the theoretical landscape of differential geometry with the nuanced perspectives afforded by this advanced conceptual framework.

4.1 Self-dual Yang-Mills fields on self-dual manifolds

Among the seminal contributions in the study of differential geometry, the work presented in [1] stands out by elucidating a profound connection between self-dual Yang-Mills fields on a four-manifold and holomorphic vector bundles over the associated twistor space. This relationship, bridging the gap between real and complex geometries, has paved the way for significant advancements in understanding gauge theories and complex differential geometry.

The Atiyah-Hitchin-Singer (AHS) theorem provides a concrete manifestation of this connection, which can be summarized as follows:theorem

Theorem I (Atiyah-Hitchin-Singer,[1] ). Given an oriented four-manifold \( M \) , the imposition of a conformal structure on \( M \) induces an almost complex structure on the projectivized negative spinor bundle \( P(V_{-}) \) associated with \( M \) . This almost complex structure is integrable if and only if the anti-self-dual part of the Weyl tensor, denoted by \( W_{-} \) , vanishes. In particular, integrability is guaranteed if \( M \) exhibits a self-dual conformal structure.

This result provides a geometric interpretation of self-duality in terms of complex structures, offering insights into the conditions under which a four-manifold can be described in the language of twistor theory.

Building on this foundation, the AHS theorem further elaborates on the behavior of vector bundles in this geometric framework:

Theorem II (Atiyah-Hitchin-Singer, [1]). Let \( E \) be a complex vector bundle equipped with a compatible connection and endowed with a self-dual connection over a self-dual four-manifold \( M \) . Denote the projection map by \( p:P(V_{-})→M \) and consider the pullback bundle \( F=p^{*}E \) over \( P(V_{-}) \) . Then, the following statements hold true:

1 The bundle \( F \) admits a holomorphic structure on \( P(V_{-}) \) ;

2 The bundle \( F \) is holomorphically trivial along each fiber of the twistor projection.

The significance of these theorems cannot be overstated as they provide a bridge between the physical interpretation of self-dual Yang-Mills fields and the geometric language of holomorphicity on twistor spaces. This duality not only enriches our theoretical understanding but also offers new tools and perspectives for tackling complex problems in both pure mathematics and theoretical physics.

In light of these results, our paper aims to further investigate the ramifications of the AHS theorems, exploring their implications for modern theories and highlighting potential avenues for research that emanate from this profound interplay between different geometric structures.

4.2 The dg-category of Cohesive Modules \( P_{A} \)

Assume \( A=(A^{•},d) \) is a differential graded algebra with non-negative degrees such that \( A^{k} \) is flat over \( A=A^{0} \) . Our category \( P_{A} \) comprises unique types of \( A \) -modules. We begin with a \( Z \) -graded right module \( E^{•} \) over \( A \) .

Definition 4.1 ( \( Z \) -connection). A \( Z \) -connection (or \( Z \) -graded superconnection) \( E \) is a \( k \) -linear map

\( E:E^{•}⊗_{A^{0}}A^{•}→E^{•}⊗_{A^{0}}A^{•} \)

of total degree one, satisfying the standard Leibniz condition

\( E(eω)=(E(e⊗1))ω+(-1)^{|e|}edω, \)

This connection is defined by its value on \( E^{•} \) . Let \( E_{k} \) be the component of \( E \) such that \( E_{k}:E^{•}→E^{•-k+1}⊗_{A}A^{k} \) , thus \( E=E_{0}+E_{1}+E_{2}+⋯ \) . It is clear that \( E_{1} \) is a connection on each component \( E^{n} \) in the standard sense (or the inverse of a connection if \( n \) is odd), and \( E_{k} \) is \( A \) -linear for \( k≠1 \) . Note that \( E_{0} \) is nothing but the differential of the complex \( d \) . We can see the detail of each component from the following diagram

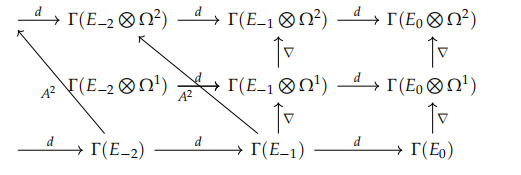
Definition 4.2 (Cohesive Modules). For a dga \( A=(A^{•},d) \) , we define the dg-category \( P_{A} \) :

1 An object \( E=(E^{•},E) \) in \( P_{A} \) , referred to as a cohesive module, is a \( Z \) -graded (but bounded in both directions) right module \( E^{•} \) over \( A \) which is finitely generated and projective, together with a \( Z \) -connection

\( E:E^{•}⊗_{A}A^{•}→E:E^{•}⊗_{A}A^{•}, \)

that satisfies the integrability condition that the curvature vanishes

\( F_{E}(e)=E∘E(e)+e⋅c=0, \)

for all \( e∈E^{•} \) .

2 The morphisms of degree \( k \) , \( P_{A}^{k}(E_{1},E_{2}) \) between two cohesive modules \( E_{1}=(E_{1}^{•},E_{1}) \) and \( E_{2}=(E_{2}^{•},E_{2}) \) are

\( ϕ:E_{1}^{•}⊗_{A}A^{•}→E_{2}^{•}⊗_{A}A^{•},|,of degreekandϕ(ea)=ϕ(e)a,∀a∈A^{•}, \)

with differential defined in the standard way

\( d(ϕ)(e)=E_{2}(ϕ(e))-(-1)^{|ϕ|}ϕ(E_{1}(e)). \)

Such a \( ϕ \) is determined by its restriction to \( E_{1}^{•} \)

We define the degree \( k \) morphisms between two cohesive modules \( E_{1}=(E_{1}^{•},E_{1}) \) and \( E_{2}=(E_{2}^{•},E_{2}) \) to be

\( \overline{Hom}^{k}(E_{1},E_{2})=\overline{Hom}_{A^{•}}^{k}(E_{1}^{•}⊗_{A^{0}}A^{•},E_{2}^{•}⊗_{A^{0}}A^{•}) \) ,

i.e. the set of degree \( k \) \( A^{•} \) -linear map from \( E_{1}^{•}⊗_{A^{0}}A^{•} \) to \( E_{2}^{•}⊗_{A^{0}}A^{•} \) . By a similar argument as above, we have

\( \overline{Hom}_{A^{•}}^{k}(E_{1}^{•}⊗_{A^{0}}A^{•},E_{2}^{•}⊗_{A^{0}}A^{•})=Hom_{A^{0}}^{k}(E_{1}^{•},E_{2}^{•}⊗_{A^{0}}A^{•}) \)

We define a differential on the morphisms \( d_{\overline{Hom}}:\overline{Hom}^{•}(E_{1},E_{2})→\overline{Hom}^{•+1}(E_{1},E_{2})→ \) by

\( d_{\overline{Hom}}(e)=E_{2}(ϕ(e))-(-1)^{|ϕ|}ϕ(E_{1}(e)). \)

It is easy to verify that \( d_{\overline{Hom}}^{2}=0 \) , and hence \( P_{A} \) is a dg-category.

Given a dg-category \( C \) , we have a subcategory \( Z^{0}(C) \) which has the same objects as \( C \) and morphisms

\( Z^{0}(C)(x,y)=Z^{0}(C(x,y)) \)

i.e. degree 0 closed morphisms in \( C(x,y) \) . On the other hand, we can form the homotopy category \( Ho(C) \) which has the same objects as \( C \) and morphisms,

\( Ho(C)(x,y)=H^{0}(C(x,y)) \)

which is the 0th cohomology of the morphism complex.

Next, we will briefly discuss the triangulated structure of cohesive modules and explore homotopy equivalences between cohesive modules.

First, we define a shift functor. For \( (E,E)∈P_{A} \) , we set \( E[1]=(E[1]=(E^{•+1},-E) \) . Next, for \( (E_{1},E_{1}),(E_{2},E_{2})∈P_{A} \) and \( ϕ∈Z^{0}P_{A}(E_{1},E_{2}) \) , we define the cone of \( ϕ \) , \( C_{ϕ}=(C_{ϕ}^{•},E_{ϕ}) \) by

\( C_{ϕ}^{•}=(\begin{matrix}E_{2}^{•} \\ ⊕ \\ E_{1}[1]^{•} \\ \end{matrix}) \)

and

\( C_{ϕ}^{•}=(\begin{matrix}E_{2} & ϕ \\ 0 & -E_{1}^{•} \\ \end{matrix}) \)

Now we have a triangle of degree 0 closed morphisms

(4.1) \( EF→C_{ϕ}→E[1] \)

Under this construction, \( P_{A} \) is pre-triangulated, and \( Ho(P_{A}) \) is triangulated with the collection of distinguished triangles being isomorphic to form 4.1.

A degree 0 closed morphism \( ϕ∈P_{A}(E_{1},E_{2}) \) is a homotopy equivalence if it induces an isomorphism in \( Ho(P_{A}) \) . We will give a simple criterion to determine whether a map is a homotopy equivalence. Consider the following decreasing filtration

\( F^{k}P_{A}(E_{1},E_{2})={ϕ∈P_{A}(E_{1},E_{2})|ϕ^{i}=0fori \lt k} \)

Lemma 4.3. There exists a spectral sequence

\( E_{0}^{pq}⇒H^{p+q}(P_{A}(E_{1},E_{2})) \)

Where

\( E_{0}^{pq}=gr(P_{A}(E_{1},E_{2}))={ϕ^{p}∈(P_{A})^{p+q}(E_{1},E_{2}):E_{1}^{•}→E_{2}^{•+q}⊗_{A_{0}}A^{p}} \)

with differential \( d_{0}(ϕ^{p})=E_{2}∘ϕ^{p}-(-1)^{p+q}ϕ^{p}∘E_{1} \) .

Proposition 4.4. A closed morphism \( ϕ∈(P_{A})^{0}(E_{1},E_{2}) \) is a homotopy equivalence if and only if \( ϕ^{0}:(E_{1}^{bt},E_{1})→(E_{2}^{bt},E_{2}) \) is a quasi-isomorphism of complexes of \( A^{0} \) -modules.

Proof. Follows from .[5]

4.3 Cohesive Self-dual Yang-Mills Modules

Next, let’s introduce cohesive modules over self-dual manifolds.

Let \( X \) be a compact self-dual four manifold, then by construction in the self-dual Yang-Mills fields is encoded in the following dga

\( \begin{matrix}Ω^{0}(X,g_{P})Ω^{1}(X,g_{P})Ω_{-}^{2}(X,g_{P}) \\ \\ ⨁ ⨁ \\ \\ Ω_{-}^{2}(X,g_{P})Ω^{3}(X,g_{P})Ω^{4}(X,g_{P}) \\ \\ deg=1 0 -1 -2 \\ \end{matrix} \)

denote this by \( A_{SD} \) (see also [6]). We call \( A_{SD} \) self-dual Yang Mills dga.

Proposition 4.5.. Fintely generated projective modules over dga \( A_{SD} \) is 1-1 corresponded to self-dual Yang-Mills fields.

Proof. By Serre-Swan theorem, vector bundles, i.e. fintely generated locally free sheave over \( O_{X}=C^{∞}(X) \) is 1-1 corresponded to fintely generated projective modules over \( Γ(O_{X}) \) , i.e. the algebra of global sections of \( O_{X} \) . Hence it suffices to verify self dual connections over \( M \) corresponds to integrability of \( A \) .

( \( → \) ) Given a vector bundle \( (E,∇) \) with self-dual connection. Regard \( E=g_{P} \) as an adjoint bundle with structured group \( G \) . Then \( F_{∇_{0}}=0∈Ω_{-}^{2}(X,g_{P})=0 \) by constrcution. Hence the top row of \( A \) is a chain complex, and the remaining part clearly gives a dga as a part of de Rham dga. The bottom part is the corresponding local BV-complex (with local antibracket taking values in the densities on \( X \) ).

( \( ← \) ) This part is trivial. Given a fintely generated projective modules over dga \( A_{SD} \) , we can construct the connection \( ∇ \) locally to be the product of the differential \( d \) coming from \( ASD \) . Clearly \( F_{∇_{0}}=0∈Ω_{-}^{2}(X,g_{P})=0 \) .

As a generalization of vector bundles, cohesive modules provides an dg enhancement to category of bundles and sheaves encoutered in differential and algebraic geometry. The first import theorem using this idea is on study the holomorphic structure of coherent sheaves over compact complex manifolds.

Theorem 4.6. ([3]). Let \( X \) be a compact complex manifold, and \( A=Ω^{0,•}X \) be the Dolbeault dga. The homotopy category of the dg-category \( P_{A} \) is equivalent to the bounded derived category of chain complexes of sheaves of \( O_{X} \) -modules with coherent cohomology on \( X \) .

Enlighted by this theorem, we define a counterpart in self-dual Yang-Mills fields:

Definition 4.7. We define cohesive self-dual Yang-Mills modules to be cohesive modules \( (E^{•},E) \) over the self-dual Yang-Mills dga \( A_{SD} \) .

Hence we have the following diagram, where the right vertical arrow is the twistor correspondence (Penrose construction) in Theorem 2. Hence it is natural to guess whether the left vertical arrow also induces a correspondence.

\( \begin{matrix}Cohesice Self-dual Yang-Mills modules & & Self-dual Yang-Mills Fields \\ ↓correspondence? & & ↓twistor correspondence \\ Holomorphic cohesive modules & & Holomorphic vector bundles \\ \end{matrix} \)

In fact, we can extend the twistor correspondence to the level of cohesive modules.

Proposition 4.8. The twistor correspondence (or Atiyah-Ward correpondence) induces a dg-quasi-equivalence between dg category \( P_{A_{SD}} \) and the dg category of holomorphic cohesive modules \( P_{A_{Hol}} \) on the twistor spaces.

Proof. Let \( X \) be a compact self dual 4-manifold and \( Z \) to be its twistor space. Suppose \( (V,∇) \) is a self-dual Yang-Mills fields on \( X \) . Then following the theorem 3.2.7 in [Block]

Theorem 4.9 (Block[3]). Suppose \( (A^{•},d,c) \) is a curved dga. Let \( X=(X,∇) \) be a quasi-cohesive module over \( A^{•} \) , then there is an object \( E=(E^{•},∇ \prime ) \) in \( P_{A^{•}} \) such that \( \widetilde{h}_{X} \) is quasi-isomorphic to \( h_{E} \) , under either of the two following conditions:

1 X is a quasi-finite quasi-cohesive module.

2 \( A^{•} \) is flat over \( A^{0} \) and there exists a bounded complex \( (E,∇ \prime ^{0}) \) of finitely generated projective right \( A^{0} \) -modules and an \( A^{0} \) -linear quasi-isomorphisms \( e^{0}:(E,∇ \prime ^{0})→(X,∇^{0}) \) .

and the proof of lemma 4.1.5, we can construct a cohesive self-dual Yang-Mills module \( (E^{•},E) \) which is quasi-isomorphic to \( (V,∇) \) . On the other hand, by Theorem 2 from [1], \( (V,∇) \) is 1-1 corresponding to a holomorphic vector bundle \( (W,∇_{∂}) \) on the twistor space, which is in turn quasi-isomorphic to a holomorphic cohesive module \( (F^{•},F) \) .

Now let’s construct a \( A_{SD}-A_{Hol} \) -cohesive-bimodule by letting

\( X^{•}=Γ(X,Hom(E^{•},F^{•})) \)

where the morphism between \( E^{•},F^{•} \) is naturally defined as a map from bundles over \( X \) to its twistor space. Then by definition 3.1.1 in , this bimodule induces a quasi-equivalence between dg category of cohesive self-dual Yang Mills modules \( P_{A_{SD}} \) and the dg category of holomorphic cohesive modules \( P_{A_{Hol}} \) on the twistor spaces since 1) by our construction it induces quasi-equivalence in hom set and equivalence on the homotopy categories (II).

5 Conclusion

The exploration of self-duality in the context of Yang-Mills theory, complex structures, and twistor spaces has revealed profound connections between the geometry of four-dimensional manifolds and the physics of gauge theories. Through the differential geometric lens, we have gained insights into the rich interplay between topological, algebraic, and analytic structures that underlie these theories.

The use of self-dual Yang-Mills fields and their relationship with holomorphic complex structures on twistor spaces has provided a powerful framework for understanding the geometry of gauge fields. The ability to reinterpret gauge field configurations in terms of holomorphic data on the twistor space has not only deepened our mathematical understanding but also offered new tools for tackling physical problems.

Moreover, the introduction of cohesive modules over self-dual manifolds has extended our perspective beyond traditional approaches. By incorporating the language of differential graded algebra and categories, we have established a more nuanced understanding of deformations, stability, and classification of geometric objects, such as vector bundles and sheaves.

This paper has laid the groundwork for further research into the correspondence between self-dual Yang-Mills fields and holomorphic vector bundles. The cohesive module framework opens up new avenues for exploring the moduli spaces of solutions to the Yang-Mills equations, as well as their implications for quantum field theory and string theory.

The results presented in this paper also invite further investigation into the connections between the geometry of four-dimensional manifolds and other physical theories, such as general relativity and supersymmetry. The interplay between mathematics and physics continues to be a fertile ground for discovery, and the tools developed here will undoubtedly contribute to this ongoing dialogue.

Acknowledgments

The author would like to extend their heartfelt gratitude to Dr. Zeng, who discussed the research paper with the author over and over. He served as an invaluable mentor, providing insightful feedback on the edition of the paper.