1 Introduction

Quantum information processing has been a key task in applying quantum mechanics in recent decades. Ref. [1] introduced quantum communication using measurements on entangled Bell states. In Ref [2], the authors studied Teleporting an Unknown Quantum State through Dual Classical and Einstein-Podolsky-Rosen Channels. In Ref [3], what kinds of Fundamental limits will repeaterless quantum communications have been introduced by authors? The authors talked about a photonic integrated quantum secure communication system In Ref [4]. In Ref [5], the author discussed the method of quantum teleportation, about Ground-to-satellite. In Ref [6], light-to-motion Quantum teleportation was studied by the author. In Ref [7], N. Fiaschi and his team introduced Optomechanical quantum teleportation. In Ref [8], T. M. Graham’s team used hyperentangled photons for Superdense teleportation. In Ref [9], the way of Probabilistic implementation operation by using a nonminimally entangled state introduced by L. Chen and Y.-X. Chen. In Ref [10], A. S. Cacciapuoti and his team studied quantum teleportation for the quantum internet, as entanglement meets classical communications. In Ref [11], a study of security during quantum dense coding in high-dimensions was introduced by Y.-X. Zhang’s team. In Ref [12], A. Fonseca studied when noisy environments, and the condition of high-dimensional quantum teleportation. In Ref [13], a team of F. Shi introduced information masking in k-uniform quantum. In Ref [14], Y.-H. Luo’s team studied in high dimensions, what quantum teleportation will be like. In Ref [15], a team of A. Barenco introduced quantum computation’s Elementary gates.

2 Preliminaries

Here are some useful explanations for the mathematics that will be used. In this section, we introduce some useful explanations of the mathematics and notations that will be used in this paper. In Sec. 2.1, we review matrix basics and Kronecker products. Then we introduce the basic knowledge from quantum mechanics such as quantum states, Ket-bra notations, and entanglement. In Sec. 2.3, we introduce the fundamental idea of standard dense coding protocol for two systems.

2.1 Matrix basics

For matrix A n x p, and matrix B m x q,

A ⊗ B = \( [\begin{matrix}a_{1,1}B & ⋯ & a_{1,p}B \\ ⋮ & ⋱ & ⋮ \\ a_{n,1}B & ⋯ & a_{n,p}B \\ \end{matrix}] \) . (1)

Generally,

A ⊗ B \( ≠ \) B ⊗A, (2)

Except when a is a scalar:

a ⊗ A = A⊗a = aA, (3)

Or if a and b are vectors.

\( a^{T} \) ⊗ b = b \( a^{T} \) = b ⊗ \( a^{T} \) . (4)

Furthermore, these formulas can be proved:

A ⊗ (B ⊗ C) = (A⊗ B) ⊗ C. (5)

A⊗(B+C)=(A⊗B)+(A⊗C). (6)

(A+B)⊗C =(A⊗C)+(B⊗C). (7)

For a matrix U, it has

\( U^{†}U \) = \( UU^{†} \) = \( I​_{n} \) (8)

2.2 quantum mechanics basics

When writing |0>, which is called ket zero, it has: = \( [\begin{matrix}1 \\ 0 \\ \end{matrix}] \) .

|0> = \( [\begin{matrix}1 \\ 0 \\ \end{matrix}] \) . (9)

Similarly, for |1>:

|1> = \( [\begin{matrix}0 \\ 1 \\ \end{matrix}] \) .(10)

If want to calculate |0> ⊗ |0>, which is always be written as |00>, according to (11):

|00>= |0> ⊗ |0> = \( [\begin{matrix}1 \\ \begin{matrix}0 \\ \begin{matrix}0 \\ 0 \\ \end{matrix} \\ \end{matrix} \\ \end{matrix}] \) . (11)

To calculate |1>⊗ |1>, similarly, written as |11>, = |1>⊗ |1>= \( [\begin{matrix}0 \\ \begin{matrix}0 \\ \begin{matrix}0 \\ 1 \\ \end{matrix} \\ \end{matrix} \\ \end{matrix}] \)

|11>= |1>⊗ |1>= \( [\begin{matrix}0 \\ \begin{matrix}0 \\ \begin{matrix}0 \\ 1 \\ \end{matrix} \\ \end{matrix} \\ \end{matrix}] \) . (12)

For information \( \frac{|00 \gt +|11 \gt }{\sqrt[]{2}} \) , when it be polluted as cos \( θ \) |00> + sin \( θ \) |11>, \( θ∈[0,\frac{π}{2}] \) , the expectation of getting the correct message from the polluted message is

E ( \( φ(θ) \) )= \( -( cosθ)^{2}log_{2} \) \( ( cosθ)^{2} \) - \( ( sinθ)^{2}log_{2} \) \( ( sinθ)^{2} \) . (13)

Assume that there exists a space with length x, breadth y, and height z, within time t, and a particle is moving inside of it, the cumulation of probability will be 1.

2.3 dense coding of two parties

In this subsection, we introduce the knowledge and terminology used in this paper. We also review the standard protocol of dense coding. Source S generates an EPR pair shared by Alice and Bob, who can have any distance, for example, which is defined as:

\( |ф^{+} \gt = \frac{1}{\sqrt[]{2}}(|00 \gt +|11 \gt ). \) (14)

To get this,

\( CNOT(H⊗I)|00 \gt = |ф^{+} \gt \) . (15)

It can be shown as:

\( [\begin{matrix}\begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} \\ \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} & \begin{matrix}0 & 1 \\ 1 & 0 \\ \end{matrix} \\ \end{matrix}]\frac{1}{\sqrt[]{2}}[\begin{matrix}\begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} \\ \begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}-1 & 0 \\ 0 & -1 \\ \end{matrix} \\ \end{matrix}] [\begin{matrix}1 \\ \begin{matrix}0 \\ 0 \\ 0 \\ \end{matrix} \\ \end{matrix}]= \frac{1}{\sqrt[]{2}} [\begin{matrix}1 \\ \begin{matrix}0 \\ 0 \\ -1 \\ \end{matrix} \\ \end{matrix}] \) . (16)

The graph of the Quantum Circuit is like this:

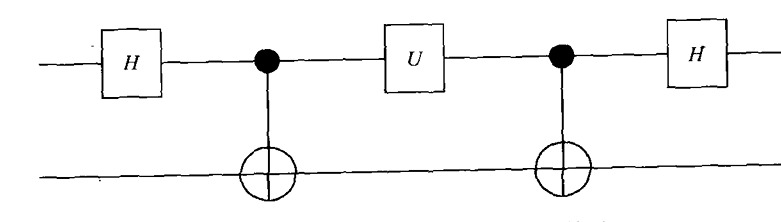
Figure 1. graph of the Quantum Circuit

Alice wants to send two bits to Bob, which could have 4 possible forms: 00, 11, 01 10. To do this, she needs to separately do the following Unitary operations:

U = I, \( iσ_{y} \) , \( σ_{x} \) , \( σ_{z} \) (17)

For example, if she wants to pass 01, the operation is:

\( σ_{x}⊗I |ф^{+} \gt =|Ψ^{+} \gt \) . (18)

In the matrix, it can be shown as:

\( [\begin{matrix}\begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} & \begin{matrix}0 & 1 \\ 1 & 0 \\ \end{matrix} \\ \begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} \\ \end{matrix}]\frac{1}{\sqrt[]{2}} [\begin{matrix}1 \\ \begin{matrix}0 \\ 0 \\ 1 \\ \end{matrix} \\ \end{matrix}]= \frac{1}{\sqrt[]{2}} [\begin{matrix}0 \\ \begin{matrix}1 \\ 1 \\ 0 \\ \end{matrix} \\ \end{matrix}] \) . (19)

To learn about what Alice passed, Alice needs to pass her EPR pair to Bob at first, but if Robert, for example, gets only Bob’s pair, without Alice’s, when he tries to learn about the whole system, suppose \( e_{0}=(\begin{matrix}0 \\ 1 \\ \end{matrix}), e_{1}=(\begin{matrix}1 \\ 0 \\ \end{matrix}) \) , | \( a \gt \) = \( |ф^{±} \gt ,|Ψ^{±} \gt ; \) and | \( a \) > = \( ( \lt a|)^{†} \) , where | \( a \gt \) is the entangled state shared by both the pairs. Robert will always obtain

\( Tr_{A} \) | \( a \gt \lt a|_{AB} \) = \( \sum_{i=0}^{1} (I_{2}⊗ e_{i}^{T}) \) | \( a \gt \lt a| \) \( (I_{2}⊗ e_{i}) \) = \( ρ_{B} \) = \( \frac{1}{2}I_{2} \) . (20)

By the way, if Alice’s EPR pair was obtained by Robbert, for example, When he tries to decode it, he always obtains \( ρ_{A} \) equal to \( \frac{1}{2}I_{2} \) in terms of (7).

So the formal operation is: Bob transforms the Bell state into the computational basis states, could be written as:

\( CNOT(H⊗I)^{-1}= (H⊗I)CNOT \) . (21)

In matrix:

B = \( \frac{1}{\sqrt[]{2}}[\begin{matrix}\begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}0 & 1 \\ 1 & 0 \\ \end{matrix} \\ \begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}0 & -1 \\ -1 & 0 \\ \end{matrix} \\ \end{matrix}] \) . (22)

So it is easy to find that:

B \( |Ψ^{+} \gt =|01 \gt , B |Ψ^{-} \gt =|11 \gt \) , (23)

B \( |ф^{+} \gt =|00 \gt , B|ф^{-} \gt =|10 \gt \) .

In general physics, this dense coding is impossible because no matter how it is measured, the coded object will stay the same. Also, in this condition, when the divided message is put together, the complete information will be obtained, like puzzles. However, in quantum physics, the way the object is measured will affect the code, and the information won’t work like puzzles.

3 Multiqubit Dense Coding

In this section, we introduce a generalized protocol of dense coding in which Alice sends messages to both Bob and Charlie.

Considering a situation if S generates a three EPR pair shared to Alice, Bob, and Charlie, who can have any distance, for example, which is defined as:

\( |Ψ^{+} \gt = \frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ) \) .

Depending on which kind of information Alice wants to pass, she can make following operations:

\( I_{2}⊗I_{4} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ) \) ,

\( σ_{x}⊗I_{4} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt \) ),

\( σ_{z}⊗I_{4} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) ,

\( iσ_{y}⊗I_{4} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|011 \gt -|100 \gt \) ),

After Alice making the similar operation like before, when Robert get Bob and Charlie’s EPR pair, without Alice’s. And when he tries to get the whole system, similar as formula 20, Robert will always get:

\( Tr_{A} \) | \( a \gt \lt a|_{ABC} \) = \( \sum_{i=0}^{1} (e_{i}^{T}⊗I_{4}⊗I_{4} ) \) | \( a \gt \lt a| \) \( (e_{i}⊗I_{4}⊗I_{4}) \) = \( ρ_{BC} \) .

The expression of \( ρ_{BC} \) depends on that of \( |a \gt \) . If Robert takes | \( a \gt \) as | \( a \gt \) = \( \frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt ) \) , then \( ρ_{BC}= \frac{1}{2}[\begin{matrix}\begin{matrix}1 & 0 \\ 0 & 0 \\ \end{matrix} & \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} \\ \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} & \begin{matrix}0 & 0 \\ 0 & 1 \\ \end{matrix} \\ \end{matrix}] \) . If he takes | \( a \gt \) as | \( a \gt \) = \( \frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ), \( then ρ_{BC}= \frac{1}{2}[\begin{matrix}\begin{matrix}0 & 0 \\ 0 & 1 \\ \end{matrix} & \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} \\ \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} & \begin{matrix}1 & 0 \\ 0 & 0 \\ \end{matrix} \\ \end{matrix}] \) . So he can’t find out which one is the actually value of |a> according to the \( ρ_{BC} \) he get.

Forget about Robert. When Bob gets Alice’s pair after Alice finishes her operation, which keeps the pair as \( |Ψ^{+} \gt , \) for example, he doesn’t need to get Charlie’s pair, he just needs to communicate with Charlie to learn about the condition.

Bob can use the machine in the lab to measure the two pairs he gets. He may get \( P_{1}=|00 \gt \lt 00|+|11 \gt \lt 11| \) , or \( P_{2}=|01 \gt \lt 01|+|10 \gt \lt 10| \) , no matter what \( P_{1} \) and \( P_{2} \) is,

\( P_{1} \) + \( P_{2} \) = \( I_{4} \) .

We have two cases (i) and (ii), namely Bob obtains the measurement results P1 and P2, respectively.

Assume that Bob gets \( P_{1} \) , and as he has no idea if the pair is equal to what, he will do the following operation, for example, he takes the pair equal to \( \frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ):

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ) = 0.

As the result is equal to 0, the pair will not be equal to \( \frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ). But if he tries \( \frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) , he will get:

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|00 \gt +|11 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt ) \) ,

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|00 \gt +|11 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt -|1 \gt ) \) .

So, it can be one of \( \frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) . To learn about which one is the real value, Bob once again sent his pairs to the machine, then he will get one value from \( Q_{1} \) , \( Q_{2}, Q_{3} \) . Similarly, no matter how,

\( Q_{1} \) \( + Q_{2}+Q_{3} \) = \( I_{4} \) .

Assume that

\( Q_{1}= \frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{ \lt 00|+ \lt 11|}{\sqrt[]{2}} \) ,

\( Q_{2}= \frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{ \lt 00|- \lt 11|}{\sqrt[]{2}} \) ,

\( Q_{3} \) = |01><01| + |10><10|.

One can verify that Bob cannot obtain \( Q_{3} due to zero probablity. So we focus on two cases, Q1 and Q2. \)

If Bob gets \( Q_{1} \) , then he obtains

\( (Q_{1}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

\( (Q_{1}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

After that he communicates with Charlie to learn about what the state is.

If Bob gets \( Q_{2} \) , then he obtains

\( (Q_{2}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

\( (Q_{2}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

After that he communicates with Charlie to learn about what the state is.

Assume that bob get \( P_{2}=|01 \gt \lt 01|+|10 \gt \lt 10| \) , and as he has no idea of the pair is equal to what, he will do the following operation, for example, he takes the pair equal to \( \frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ):

\( (P_{2}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ) = 0.

As the result is equal to 0, the pair will not be equal to \( \frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ). But if he tries \( \frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) , he will get

\( (P_{2}⊗I_{4})\frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|10 \gt +|01 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt ) \) ,

\( (P_{2}⊗I_{4}) \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|10 \gt +|01 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt -|1 \gt ) \) .

So, it can be one of \( \frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) . To learn about which one is the real value, Bob once again sent his pairs to the machine, then he will get one value from \( R_{1} \) , \( R_{2}, R_{3} \) . Similarly, no matter how,

\( R_{1} \) \( + R_{2}+R_{3} \) = \( I_{4} \) .

Assume that

\( R_{1}= \frac{|01 \gt +|10 \gt }{\sqrt[]{2}}\frac{ \lt 01|+ \lt 10|}{\sqrt[]{2}} \) ,

\( R_{2}= \frac{|01 \gt -|10 \gt }{\sqrt[]{2}}\frac{ \lt 01|- \lt 10|}{\sqrt[]{2}} \) ,

\( R_{3} \) = |00><00| + |11><11|.

One can verify that Bob cannot obtain

\( R_{3} \) due to the zero probability, so we focus on \( R_{1}, R_{2} \) :

If Bob gets \( R_{1} \) , then he obtains

\( (R_{1}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

\( (R_{2}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

After that he communicates with Charlie to learn about what the state is.

If Bob gets \( Q_{2} \) , then he obtains

\( (R_{1}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

\( (R_{2}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

After that he communicates with Charlie to learn about what the state is.

We stress that, if Alice does not trust Bob, then Alice may ask Charlie to stop the communication with Bob so that Bob has no way to figure out the code from Alice. In this sense, the security of three-party dense coding is again guaranteed by the basic rules of quantum mechanics.

In the following, we extend the above scheme to a multiqubit case. For this purpose, we introduce the multipartite GHZ state as follows.

Considering a situation if S generates a multiple EPR pair shared to Alice, Bob, Charlie and etc.., who can have any distance, for example, which is defined as:

\( |Ψ^{+} \gt = \frac{1}{\sqrt[]{2}}(|0……0 \gt +|1……1 \gt ) \) .

Depending on which kind of information Alice wants to pass, she can make following operations:

\( I_{2}⊗I_{2^{n}} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|00……0 \gt +|11……1 \gt ) \) ,

\( σ_{x}⊗I_{2^{n}} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|100……0 \gt +|011……1 \gt \) ),

\( σ_{z}⊗I_{2^{n}} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|00……0 \gt -|11……1 \gt ) \) ,

\( iσ_{y}⊗I_{2^{n}} |GHZ \gt =\frac{1}{\sqrt[]{2}}(|011…1 \gt -|100……0 \gt \) ),

After Alice making the similar operation like before, when Robert get Bob and Charlie’s EPR pair, without Alice’s. And when he tries to get the whole system,

After Alice making the similar operation like before, when Robert get everyone’s EPR pair, but without Alice’s. And when he tries to get the whole system, similar as formula 20, Robert can’t find out which one is the actually value of |a> according to the \( ρ_{BC…} \) he gets.

Forget about Robert. Set Bob’s pair as \( B_{1} \) , others as but not including Alice, as \( B_{n}. \) When Bob gets Alice’s pair after Alice finishes her operation, which keeps the pair as \( |Ψ^{+} \gt , \) for example, he doesn’t need to get others pair, he just needs to communicate with them to learn about the condition.

Bob can use the machine in the lab to measure the two pairs he gets. He may get \( P_{1}=|000 \gt \lt 0…0|+|11 \gt \lt 11| \) , or \( P_{2}=|01 \gt \lt 01|+|10 \gt \lt 10| \) , no matter what \( P_{1} \) and \( P_{2} \) is,

\( P_{1} \) + \( P_{2} \) = \( I_{4} \) .

We have two cases (i) and (ii), namely Bob obtains the measurement results P1 and P2, respectively.

Assume that Bob gets \( P_{1} \) , and as he has no idea if the pair is equal to what, he will do the following operation, for example, he takes the pair equal to \( \frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ):

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ) = 0.

As the result is equal to 0, the pair will not be equal to \( \frac{1}{\sqrt[]{2}}(|100 \gt ±|011 \gt \) ). But if he tries \( \frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) , he will get:

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|00 \gt +|11 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt ) \) ,

\( (P_{1}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|00 \gt +|11 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt -|1 \gt ) \) .

So, it can be one of \( \frac{1}{\sqrt[]{2}}(|000 \gt +|111 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|000 \gt -|111 \gt ) \) . To learn about which one is the real value, Bob once again sent his pairs to the machine, then he will get one value from \( Q_{1} \) , \( Q_{2}, Q_{3} \) . Similarly, no matter how,

\( Q_{1} \) \( + Q_{2}+Q_{3} \) = \( I_{4} \) .

Assume that

\( Q_{1}= \frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{ \lt 00|+ \lt 11|}{\sqrt[]{2}} \) ,

\( Q_{2}= \frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{ \lt 00|- \lt 11|}{\sqrt[]{2}} \) ,

\( Q_{3} \) = |01><01| + |10><10|.

One can verify that Bob cannot obtain \( Q_{3 } \) due to zero probablity. So we focus on two cases, \( Q_{1} \) and \( Q_{2} \) .

If Bob gets \( Q_{1} \) , then he obtains

\( (Q_{1}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

\( (Q_{1}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

After that he communicates with others to learn about what the state is.

If Bob gets \( Q_{2} \) , then he obtains

\( (Q_{2}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

\( (Q_{2}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|00 \gt -|11 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|00 \gt +|11 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

After that he communicates with others to learn about what the state is.

Assume that bob get \( P_{2}=|01 \gt \lt 01|+|10 \gt \lt 10| \) , and as he has no idea of the pair is equal to what, he will do the following operation, for example, he takes the pair equal to \( \frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ):

\( (P_{2}⊗I_{4})\frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ) = 0.

As the result is equal to 0, the pair will not be equal to \( \frac{1}{\sqrt[]{2}}(|000 \gt ±|111 \gt \) ). But if he tries \( \frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) , he will get

\( (P_{2}⊗I_{4})\frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|10 \gt +|01 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt ) \) ,

\( (P_{2}⊗I_{4}) \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) = \( \frac{1}{\sqrt[]{2}}(|10 \gt +|01 \gt ) \) \( ⊗\frac{1}{\sqrt[]{2}}(|0 \gt -|1 \gt ) \) .

So, it can be one of \( \frac{1}{\sqrt[]{2}}(|100 \gt +|011 \gt ), \) or \( \frac{1}{\sqrt[]{2}}(|100 \gt -|011 \gt ) \) . To learn about which one is the real value, Bob once again sent his pairs to the machine, then he will get one value from \( R_{1} \) , \( R_{2}, R_{3} \) . Similarly, no matter how,

\( R_{1} \) \( + R_{2}+R_{3} \) = \( I_{4} \) .

Assume that

\( R_{1}= \frac{|01 \gt +|10 \gt }{\sqrt[]{2}}\frac{ \lt 01|+ \lt 10|}{\sqrt[]{2}} \) ,

\( R_{2}= \frac{|01 \gt -|10 \gt }{\sqrt[]{2}}\frac{ \lt 01|- \lt 10|}{\sqrt[]{2}} \) ,

\( R_{3} \) = |00><00| + |11><11|.

One can verify that Bob cannot obtain

\( R_{3} \) due to the zero probability, so we focus on \( R_{1}, R_{2} \) :

If Bob gets \( R_{1} \) , then he obtains

\( (R_{1}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

\( (R_{1}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|10 \gt +|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

After that he communicates with others to learn about what the state is.

If Bob gets \( Q_{2} \) , then he obtains

\( (R_{2}⊗I_{2})_{AB⊗C} |a_{2} \gt =\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt -|1 \gt )=\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ -1 \\ \end{matrix}) \) ,

\( (R_{2}⊗I_{2})_{AB⊗C} |a_{1} \gt =\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(|0 \gt +|1 \gt )=\frac{|10 \gt -|01 \gt }{\sqrt[]{2}}\frac{1}{2}(\begin{matrix}1 \\ 1 \\ \end{matrix}) \) ,

After that he communicates with others to learn about what the state is.

We stress that, if Alice does not trust Bob, then Alice may ask Charlie to stop the communication with Bob so that Bob has no way to figure out the code from Alice. In this sense, the security of three-party dense coding is again guaranteed by the basic rules of quantum mechanics.

4 Conclusion

We have presented a new protocol of multiqubit super dense coding, by using the multiqubit Greenberger-Horne-Zeilinger states. We have given details for the three-qubit case, and we extended it to the multiqubit case in a more succinct way. The next step in this paper is to study whether one can similarly construct more quantum-information processing tasks by using a similar idea, such as multipartite quantum secret sharing and masking.