1. Introduction

Reinvigorating computation, quantum computing has captured the imagination of interdisciplinary researchers and trailblazers. This revolutionary paradigm promises to transcend the boundaries of classical computing through the exclusive capabilities of quantum mechanics. Envisioned as a game-changer, it strives to tackle complex challenges with a velocity and precision unprecedented in traditional computing. Delving into its historical roots, quantum computing finds its genesis in the early 20th century, a time when intellectual giants such as Max Planck, Niels Bohr, and Werner Heisenberg laid the theoretical cornerstone for elucidating the dynamical interactions of material particles and energy phenomena on the atomic and subatomic scales. Their contributions formed the intellectual scaffolding upon which quantum computing's aspirations are built.

The impetus to leverage quantum systems for computational endeavors notably accelerated during the 1980s. Richard Feynman's seminal 1982 work, titled "Simulating Physics with Computers," underscored the inherent inefficiency of simulating quantum phenomena on classical machines, stemming from the exponential bloat of computational demands with system expansion [1]. This revelation reignited interest in exploiting the unique features of quantum mechanics for computational pursuits. Following Feynman's seminal contributions, quantum computing has undergone swift advancements, propelled by breakthroughs in quantum physics, computer science, and engineering domains. Initial endeavors concentrated on showcasing core quantum computing principles, encompassing phenomena like quantum teleportation and entanglement-mediated communication frameworks. Nonetheless, notable strides in constructing scalable quantum computing platforms, capable of tackling intricate algorithms, were not attained until the dawn of the new millennium. This achievement was fueled by substantial investments from multiple sectors, including governments, academia, and industry, acknowledging quantum computing's potential to address the humanity's most critical challenges.

In recent years, quantum computing has experienced notable advancements, with a multitude of milestones accomplished across different aspects. A particularly significant accomplishment is the development of quantum processors that possess an escalating number of qubits. Initially, quantum processors were restricted to just a few qubits, significantly constraining their computational capabilities. Nevertheless, current advanced systems now feature hundreds or even thousands of qubits, facilitating more intricate computations and expanding the horizons of quantum computing's potential. These advancements have materialized due to breakthroughs in materials science, fabrication techniques, and control electronics. Researchers have introduced innovative qubit implementations, including superconducting qubits, optical quantum, they are all presenting their own set of advantages and challenges. Furthermore, progress in microwave engineering and cryogenics has facilitated precise control and manipulation of quantum states, which is vital for executing intricate quantum algorithms.

A pivotal achievement in the evolution of quantum computing lies in the demonstration of what is known as 'quantum supremacy,' a term coined by John Preskill. This concept highlights the quantum computer's capacity to execute a designated task at a pace unparalleled by any classical computer, even when the latter employs immense parallel processing capabilities [2]. Notably, in 2019, Google asserted that it had achieved this quantum supremacy milestone with its 53-qubit 'Sycamore' processor. This accomplishment entailed solving a random circuit sampling problem in merely 200 seconds, a feat that would have ostensibly consumed millennia for even the world's swiftest supercomputer [3]. Amidst ongoing discussions regarding the significance and repercussions of this breakthrough, it stands as a pivotal step in showcasing the immense potential harbored by quantum computing.

The motivation behind this paper stems from the growing recognition of the importance of quantum computing in addressing challenges that currently exceed the capabilities of classical computing. With computational problems continually increasing in complexity, there is a pressing need for innovative computational paradigms that can handle the exponential growth in computational demands. Quantum computing emerges as a promising solution, leveraging the unique properties of quantum mechanics to achieve substantial speedups for certain classes of problems. The organization of this paper is structured as following. Sec. 2 delves into the intricacies of quantum entanglement, the unconventional correlation underpinning the prowess of quantum computing. Sec. 3 outlines the fundamental principles of quantum computation, encompassing qubits and quantum gates, supported by mathematical formulations and visual aids. Sec. 4 explores the cutting-edge applications of quantum computing, showcasing recent triumphs and outcomes stemming from these groundbreaking technologies. Sec. 5 contrasts quantum algorithms with their classical counterparts, elucidating their advantages and potential benefits. Sec. 6 appraises the existing constraints within quantum computing and provides insights into prospective research avenues and the future landscape of this burgeoning field. Lastly, Sec. 7 concludes the paper by recapitulating the core discoveries and their broader implications.

2. Descriptions of quantum entanglement

Quantum entanglement, a singular feature of quantum mechanics, signifies an intricate interconnectedness among two or more quantum particles. This strong correlation renders the state of any one particle inseparable from the rest, transcending even spatial separation. This nonlocal aspect is among quantum mechanics' most intriguing and counter-intuitive qualities, underpinning the core tenets of quantum information processing and computation. Quantum entanglement is mathematically formulated in the realm of quantum mechanics, leveraging the constructs of linear algebra and complex Hilbert spaces. A composite quantum system's pure state, comprising two or more subsystems, can be mathematically represented as a vector residing in the tensor product of the individual subsystems' Hilbert spaces. When the state cannot be decomposed into a simple product of the individual subsystem states, it is classified as entangled, highlighting the inseparability of the system components.

Consider a two-qubit scenario where each qubit can inhabit either the |0⟩ or |1⟩ state. In this context, separable states are straightforwardly represented by |00⟩, |01⟩, |10⟩, or |11⟩. However, the Bell state \( |Φ+⟩ = (|00⟩ + |11⟩)/\sqrt[]{2} \) exemplifies entanglement, a state that resists decomposition into individual qubit states. This entanglement creates a profound connection, where the measurement of one qubit instantaneously influences the state of its entangled counterpart, defying spatial barriers. This nonlocal correlation serves as the foundation for a myriad of quantum communication and computational protocols. In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen introduced the EPR paradox [4], which questioned the completeness of quantum mechanics by asserting that entanglement contradicted local realism. Nevertheless, subsequent scientific investigations have repeatedly validated the predictions of quantum mechanics, upholding the authenticity of entanglement and its nonlocal characteristics. Quantum computing leverages entanglement to offer a fundamentally novel approach to parallel information processing compared to classical methods. By exploiting entanglement, quantum computers embark on multiple computational trajectories concurrently, harnessing the superposition principle to perform intricate computations with heightened efficiency vis-à-vis classical counterparts.

3. Principle of quantum computation

Quantum computation uniquely exploits the salient features of quantum mechanics to perform calculations in a completely distinct manner from classical computation. At its core, quantum computing relies on the qubit, a fundamental unit of information that differs markedly from the classical bit in various crucial respects. A classical bit is binary, constrained to the states 0 or 1. Conversely, a qubit boasts a super positional ability, concurrently inhabiting a blend of these two states. Mathematically, this blend is framed as a linear integration of |0⟩ and |1⟩ states, designated as ∣ψ⟩ = α∣0⟩ + β∣1⟩, where α and β are complex coefficients under the normalization rule ∣α∣² + ∣β∣² = 1. This superposition grants the qubit superior information-carrying potential over its classical counterpart, permitting it to signify a continuous spectrum of states, transcending the limitations of mere binary representation.

Quantum circuit elements, namely quantum gates, serve as the fundamental components for manipulating qubits to execute computational procedures. Distinct from classical logic gates that function sequentially on individual bits, quantum gates exhibit the capability to simultaneously interact with one or multiple qubits, leveraging the superposition and entanglement features inherent in quantum states. Several prototypical quantum gates are:

• The Hadamard Gate (H), which transforms a basis state into a superposition state. For instance, the gate transforms the state |0⟩ into an equal superposition of |0⟩ and |1⟩.

• The Controlled-NOT (CNOT) Gate, which implements a conditional NOT operation between two qubits. If the control qubit is in the |1⟩ state, the target qubit's state flips; otherwise, it remains unchanged.

• The Toffoli Gate, a universal quantum gate capable of simulating any classical logic circuit. It toggles the target qubit's state solely when both control qubits are simultaneously in the |1⟩ configuration.

• These gates underscore the quantum computing paradigm's parallel processing capabilities, enabling computations that far surpass those achievable by conventional means.

Quantum algorithms capitalize on the innate parallelism and entanglement properties of quantum computers, resulting in substantial speed enhancements compared to classical algorithms. Grover's search algorithm, for instance, achieves a quadratic speedup in identifying a target element within an unordered N-element list, requiring just O( \( \sqrt[]{N} \) ) steps, vastly superior to the O(N) steps of its classical counterparts [5]. Similarly, Shor's factorization algorithm performs the task of large integer factorization in polynomial time, whereas the most advanced classical factoring methods operate in sub exponential time, underscoring the remarkable efficiency gains offered by quantum algorithms [6]. The mathematical framework of quantum algorithms typically entails representing quantum states as vectors in a complex Hilbert space and utilizing linear algebra to depict the evolution of these states when quantum gates are applied. Illustrated in Figure 1 is a quantum circuit diagram, exemplifying the utilization of quantum gates in the manipulation of qubits.

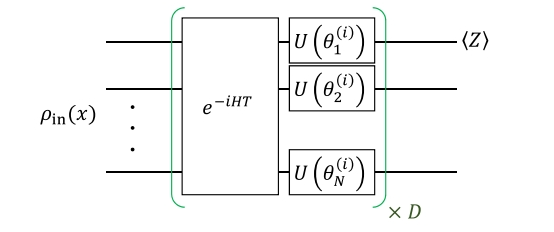
Figure 1. Quantum circuit used in numerical simulations (Photo/Picture credit: Original).

In addition to the basic algorithms, the specific implementation methods of quantum computers are also various. At present, there are several mature quantum computers. Ion trap quantum computers utilize charged ions suspended in electromagnetic fields as qubits. They offer long coherence times, high-fidelity gates, and scalability potential. Recent advances have shown stable confinement of hundreds of ions, but scaling to larger numbers remains a challenge. Advanced control techniques and cryogenic traps aim to minimize decoherence. Hybrid quantum-classical systems simplify complex algorithm implementation. Applications include quantum simulation, optimization, and cryptography. Overcoming scaling, error correction, and integration challenges is crucial for practical deployment. Despite these hurdles, ion trap quantum computers show promise for realizing fault-tolerant quantum computation [7]. Superconducting quantum computers harness the unique properties of superconducting materials at extremely low temperatures to realize efficient manipulation and stable storage of quantum bits (qubits). They leverage quantum superposition and entanglement to solve complex problems with unprecedented efficiency, far surpassing classical computers. Core to their operation are superconducting quantum chips, which serve as the foundation for qubit operations. With applications spanning drug discovery, material science, cryptography, and secure communications, superconducting quantum computers represent a promising direction in quantum computing research. Advancements such as China's indigenously developed "Origin Quantum Computing" demonstrate the practicality and sophistication of this technology [8]. Optical quantum computers constitute a cutting-edge technology that harnesses the distinct properties of light to execute computations. They employ photons as qubits, leveraging quantum superposition, interference, and entanglement to facilitate parallel processing and efficient information handling. This enables optical quantum computers to address complex problems with unprecedented speed and efficiency, surpassing the limitations of classical computers [9]. Silicon photonics computers, or silicon photonics-based computing systems, utilize silicon-based photonic integrated circuits to manipulate and process information using photons instead of electrons. This technology combines the advantages of silicon, a traditional material for integrated circuits, with the speed and bandwidth of optical communication [10]. Topological quantum computers represent a promising avenue in quantum computing research. Leveraging the topological properties of certain quantum systems, they aim to achieve fault-tolerant quantum computation. These computers encode quantum information in a manner that is intrinsically resilient to decoherence and errors, enhancing stability and reliability [11].

4. Applications for quantum computation

Quantum computation showcases immense potential across diverse application domains, ranging from optimization and machine learning to cryptography and materials science. This section delves deeper into these applications, emphasizing the recent achievements and implications stemming from advancements in quantum computing technologies. By leveraging the unique properties of quantum mechanics, quantum computing promises to revolutionize these fields and pave the way for groundbreaking solutions.

4.1. Optimization

Quantum computation presents formidable potential for tackling optimization challenges prevalent across industries like logistics, finance, and engineering. These problems necessitate pinpointing the optimal solution amidst numerous configurations, posing significant computational hurdles for classical computing frameworks. By exploiting the inherent advantages of quantum mechanics, quantum computing aims to revolutionize the resolution of such optimization tasks.

Quantum annealing, a heuristic optimization algorithm inspired by the metallurgical process of annealing, can be executed on quantum computers to discover approximate solutions for intricate optimization problems. This algorithm initializes a system of qubits in a superposition state and progressively cools it down to its ground state, where the lowest energy configuration signifies the optimal solution to the optimization problem.

4.2. Machine learning

Quantum computing presents a transformative opportunity for machine learning, promising streamlined neural network training and the emergence of innovative quantum-driven algorithms. Quantum neural networks (QNNs) capitalize on the exclusive attributes of quantum mechanics to embody and manipulate data, marking a fundamental divergence from traditional neural network architectures. This approach enables QNNs to process information in a fundamentally different manner, leveraging the inherent advantages of quantum computation for enhanced performance and efficiency. Parameterized variational quantum algorithms (pVQAs) have emerged as an encouraging approach for solving optimization challenges leveraging quantum computation. These algorithms deploy a circuit architecture parameterized by quantum gates, which encodes the solution space for a given optimization problem. The parameters of this quantum circuit are subsequently refined through a classical optimizer aimed at minimizing a predefined cost function.

This blend of quantum and classical computation has garnered attention for its application in diverse machine learning endeavors, including the development of quantum support vector machines and quantum autoencoders. By strategically combining the advantages of both paradigms, pVQAs enable the efficient tuning of sophisticated machine learning models, thereby addressing intricate optimization tasks with greater proficiency.

4.3. Cryptography

Quantum cryptography, alternatively known as quantum key distribution (QKD), promises an unparalleled level of security that transcends the limitations of classical cryptography. Drawing upon quantum mechanical principles, notably the no-cloning theorem and the uncertainty principle, QKD ensures that any interception attempt on a quantum communication channel is detectable, consequently safeguarding against unauthorized access to transmitted data [12].

In QKD, a sequence of quantum states (typically photons) is transmitted between two communicating parties. Any attempt to measure these quantum states to extract information will inevitably disturb them, revealing the presence of an eavesdropper. By monitoring the disturbance in the transmitted quantum states, the communicating parties can detect any eavesdropping attempts and abort the communication if necessary.

4.4. Material science

Quantum computing presents a transformative opportunity for material science by facilitating the simulation of intricate quantum systems that are computationally overwhelming for classical machines. Classical approaches to modeling quantum systems, encompassing molecules and solid-state materials, grapple with an exponential surge in computational intricacy as the system dimensions expand. Conversely, quantum computers excel at efficiently embodying and manipulating quantum states, rendering them ideally suited for simulating these systems with precision and efficacy.

Quantum phase estimation techniques can aid in elucidating the energy distribution of molecular Hamiltonians, a crucial aspect for deciphering the electronic configuration and chemical characteristics of molecules. This knowledge forms the cornerstone for crafting innovative materials tailored to specific attributes like heightened conductivity, sturdiness, or catalytic prowess. By mimicking the dynamics of quantum systems at an atomic level, quantum computers accelerate the quest for groundbreaking materials with transformative applications.

5. Comparison with traditional algorithms

Quantum computing algorithms exhibit notable advantages over traditional algorithms in terms of computational speed and efficiency, particularly for problems that are inherently challenging to solve using classical methods. In the realm of optimization problems, quantum annealing and QAOA can frequently discover high-quality solutions more rapidly than classical heuristics, harnessing the parallelism and entanglement properties inherent in quantum computation. Analogously, for machine learning tasks, QNNs and VQAs possess the potential to expedite training processes and enhance model accuracy by leveraging the distinct capabilities of quantum computers.

However, it is essential to recognize that quantum computing does not represent a panacea for all computational challenges. Despite the existence of problems that can be effectively tackled by conventional algorithms, the cost associated with developing and sustaining quantum computers poses a substantial obstacle for widespread adoption. Moreover, the pursuit of practical quantum algorithms that outperform their classical counterparts remains an active field of inquiry, confronted with numerous hurdles that have yet to be navigated.

6. Limitations and prospects

Quantum computing remains an emerging technology, and widespread implementation necessitates addressing numerous substantial obstacles. A pivotal challenge lies in the delicacy of qubits, which are susceptible to decoherence and noise. Decoherence arises when quantum coherence dissipates due to environmental interactions, transforming the quantum state into a classical blend. Additionally, noise may originate from various factors, including qubit realization flaws, control electronics imperfections, and ambient conditions, posing further difficulties. To address decoherence and noise issues, scientists are advancing sophisticated error mitigation techniques and constructing more resilient qubit architectures. Techniques like surface codes and topological quantum error correction are being employed, wherein logical qubits are encoded across numerous physical qubits. This approach enables the detection and correction of errors without perturbing the encoded quantum information. Nonetheless, these error correction strategies necessitate a substantial overhead, both in terms of the quantity of physical qubits required and the intricacy of the control circuitry. Another hindrance in the current landscape of quantum computing is the constraint in qubit interconnectivity within processors. Most processors sport a scattered qubit network, where direct links exist between only a select few qubits. This restricted connectivity poses obstacles for intricate quantum algorithm deployment, potentially necessitating auxiliary SWAP gates for data transfer between distant qubits. Scientists are actively investigating diverse architectural blueprints to enhance qubit connectivity, exploring options like 2D lattices, 3D arrays, and superconducting resonators, among others.

Despite these limitations, the prospects for quantum computing are bright. Advances in materials science, quantum hardware design, and algorithm development are driving rapid progress in the field. New qubit implementations, such as topological qubits and spin qubits, are being explored to improve qubit coherence times and reduce the impact of noise. Additionally, the development of hybrid quantum-classical systems that leverage the strengths of both technologies is likely to accelerate the adoption of quantum computing in the near term. Quantum computing, in the long haul, bears the capacity to transform diverse industries and enable solutions to problems that classical computers struggle with. For drug discovery, it can accelerate the identification of potential drug candidates by simulating molecular interactions at the atomic level. Analogously, in climate modeling, quantum computing can bolster simulation precision by efficiently tackling the intricate dynamics of atmospheric and oceanic systems.

7. Conclusion

In conclusion, quantum computing has emerged as a promising avenue with multifaceted applications, outperforming traditional computers in terms of computational swiftness and proficiency across domains from optimization and machine learning to cryptography and materials science. Despite formidable challenges, including qubit fragility and the necessity for practical error correction codes, the prospects for quantum computing appear bright. With relentless progress in hardware, software, and algorithmic advancements, quantum computing promises to transform into an indispensable instrument for tackling humanity's pressing challenges. Researchers and engineers are relentlessly striving to transcend the limitations of contemporary quantum technologies and extend the boundaries of quantum computing's potential. As this field continues to advance, quantum computing is poised to infuse a fresh and substantial impetus into the development of human science and technology.