1. Introduction

Quantum computation is a revolution in computer science and engineering, leveraging quantum principles and properties to exponentially improve computation speed and efficiency. Different from classical bit that can either be 0 or 1, a quantum bit can be both 0 and 1 simultaneously, along with quantum entanglement that chains multiple qubits up to let their state influence others in no time, there is a saying that “Comparing the computility of classical and quantum computer is a drop of water versus the Pacific Ocean.” This is the reason why qubit, the fundamental unit of quantum computation, is a hotspot of physics research, attracts researchers around the worlds to obsessively explore and develop.

There comes the purpose to present this article: to provide an introductory overview of qubits and quantum computation’s principle and application; to explain how quantum principles like superposition and entanglement significantly empower digital computation, in order to draw more people’s interest on quantum computation. The motivation to present this article is to attract more attention to the field, and even new talents to dedicate join the field and dedicate to its development. The achievements in quantum computation can not only empower cutting edge productive force in top scientific and military industry, but also be decentralized to civil commercial market and improve everybody’s daily life.

The banquet of quantum computation has just been started. Many different types of qubits, quantum gates, and algorithms has been under development. As well as quantum computation has already impacted various field, including cryptography, material science, and artificial intelligence, the wider the researches expand, the more challenges expose. Error correction that theoretical quantum physicsists don’t need to consider, makes a notable part of quantum computation, as an applicational science. This article reviews the basic properties of quantum computation, different types of qubits under development, methods to perform quantum computation(including logical gates and algorithms), and some example errors and correction methods. The earlier parts focus on single qubits, explicating from the basic math model to specific types qubits that have been produced, and the later parts , in a more integrated view, exemplify the designs and challenges of quantum computation. The article also includes many cutting edge achievements in vast areas made by labs and research groups around the world, including a design of laser manipulated logic gate, a method to entangle 18 qubits in lab environment, and a circuit to simulate time traveling for error correction.

2. The Properties and Different Types of Qubits

A classical bit based on a transistor can either output 0 or 1. With this limitation, for example, “14132” in binary is “11011100110100”, 14 digits, which requires 14 transistors to represent this single number in a classical computer. A qubit, in the other hand, although it technically have the same mathematical definition as a classical bit, it only takes 1 degree of freedom of a particle. Therefore, for example, a particle with 6 has the same definition as classical bit, but a particle that has more than 1 degree of freedom, can have However, since each degree of freedom can represent a qubit, it only takes 3 particles that have 6 degrees of freedom to represent the number “14132”.

2.1. Superposition and Entanglement

A classical bit is like flipping a coin; when it fall on the ground it is either front side or back side up. There are 2 possible states as the result of the event flipping coin. Nevertheless, in microscopic scale, a “coin”, which is the quantum states of a particle, is able to be both front and back side up simultaneously until it is disrupted and collapses to either side up like a real coin[1]. This combination of the basic states(eigenstates) is called “superposition”.

The probable states of a quantum system are called quantum states, which include eigenstates and the superposition. In macroscopic scale, a coin with a side facing up, assuming it is the back side, is a “fact” before and after someone check whether side facing up. However, in microscopic scale, observation or measurement is “big” enough to disrupt the system, causing it to collapse to one of its eigenstates. In the coin example mentioned above, in microscopic world, a “coin” always has both side facing up until someone makes a measurement, causing it collapse to the state that one side is facing up.

The reason is when a camera takes a picture, there must be photon entering the aperture, which fact can be ignored in macroscopic scale. However, in microscopic scale, measurement is significant enough to disrupt a particle, causing the system in its superposition to collapses. In the famous double-slits experiment, 1 single photon always go through both slits, except of it is observed, then it only go through either slit. This basic phenomenon is the essential reason that quantum teleportation is naturally spy-proof.

Quantum entanglement is another phenomenon that is against people’s common sense. In microscopic scale, when multiple particles interfere, they are integrated into a unitary system, which all the particles are correlated and every single one of them cannot be described independently, no matter how far away in distance they are separated. When 1 particle in this system is measured, all will collapse to the corresponding eigenstate at the moment, which behaves like the transformation of information is violating the limitation of light speed.

For example, there are 2 identical qubits that are both in their superposition described by equation 1, and entangled that they are always in the same state.

\( \frac{1}{\sqrt[]{2}}|0 \gt +\frac{1}{\sqrt[]{2}}|1 \gt \) (1)

Therefore, these 2 particles are either in \( |00 \gt \) or \( |11 \gt \) . If one of them is put on the Earth and the other one is put on Alpha Centauri, then someone measures and finds out the one on the Earth is in \( |0 \gt \) , the one more than 4 light years away is guaranteed to be \( |1 \gt \) instantly.

2.2. Superconducting Qubits

Superconducting qubit is a magnificent solution of quantum computation in recent years. It has advantages on scalability, gate operation speed, coupling, and more useful features.

DC Josephson effect happens when 2 superconductors only separated barely by an extremely thin insulator(NB: These conductors don’t need to be parallel), which electrons can penetrate the insulator in the form of cooper pair, creating a direct supercurrent flow through the insulator without any voltage drop. The supercurrent depends on the phase difference between the wave functions of the 2 electrons in the cooper pair is described by equation 2.

\( I = {I_{C}}sin(Δφ) \) (2)

2.3. Trapped Ion Qubits

Trapping an ion with potentials made by strong electromagnetic fields with devices such as Paul Trap or Penning Trap produces qubit highly isolated from the environment. This type of qubit has long coherence times, allow processing high fidelity quantum gate, and can be upscaled to higher computation capability by trapping multiple ions in the same trap.

Professor Rainer Blatt’s group in University of Innsbruck has made great progress on Ca⁺ and Be⁺ qubits. This group has made significant contributions on developing quantum algorithms, error correction, and quantum computer miniaturization.

2.4. Laser Manipulation

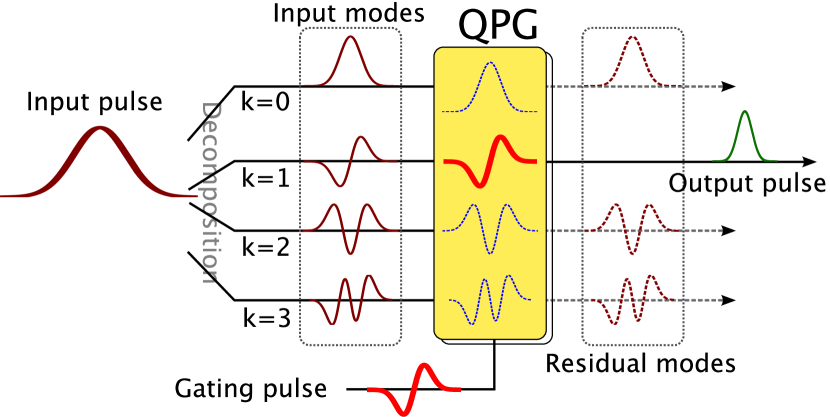
Using laser interference is a remarkable technique to render qubits. Laser can not only do the pre-lab preparation such as cooling and presetting the qubit to certain quantum state needed, but also operate specific quantum gates such as Pulse Shaping Gate and Cirac-Zoller Gate. It can also make measurement for the output.

Figure 1 describes a Pulse Shaping Gate built by a research group led by Dr. Eckstein. It picks the eigenstate corresponding to a gating pulse and fourier composite them into the output pulse.

2.5. Polarization of Photons

Linearly, photons oscillate in either the horizontal or the vertical plane. Angularly, photons electric fields either rotate in Right-Hand(clockwise) or Left-Hand(counterclockwise). These 2 degrees of freedom are not independent to each other, instead, the 4 quantum states are entangled[3], follow the relationships described by equation 3. This equation group reveals the relationship among the 4 quantum states of a photon. “H” stands for “horizontal”, “V” for “vertical”, “R” for “right(clockwise)”, and “L” for “Counter-Clockwise”.

\( |H \gt =\frac{1}{\sqrt[]{2}}(|R \gt +|L \gt ) \)

\( |V \gt =\frac{1}{\sqrt[]{2}}(|R \gt -|L \gt ) \)

\( |R \gt =\frac{1}{\sqrt[]{2}}(|H \gt +i|V \gt ) \)

\( |L \gt =\frac{1}{\sqrt[]{2}}(|H \gt -i|L \gt ) \) (3)

2.6. Photonic Qubits

Qubits made of photons exploit photons’ physical advantages. Photonic qubits experience low loss when transmitted in optical fibers, benefiting long distance communication. A photon has 3 degrees of freedoms, Photonic qubits can be easily manipulated and measured by optical components such as beam splitters, phase shifters, and wave plates. Photon, as the fastest particle, is the fastest in computation such as processing logic gates. It is also not as sensitive to temperature as superconducting qubit mentioned above. Photonic qubits in fiber-optic communication infrastructure, according to total reflection effect, don’t interfere with each other, which makes a system easily scalable and miniaturized.

Except of the 2 degrees of freedom a photon has mentioned in section 3.4, there is the 3rd degrees of freedom, which is path, the possible trajectories the photon takes. Photons can move in any direction. Therefore, a photon’s 3 degrees of freedom, polarization, orbital angular momentum, and path, make up 3 qubits.

A research group in University of Science and Technology of China, led by professor Jianwei Pan, only uses 3 photons to achieved 18 qubits’ entanglement[4]. This is the current world record of most qubit entangled artificially. The team shot a laser beam into a 3-prism-series, which ejects 2 photons to the opposite sides each, thus 6 qubits are created. Each pairs of these qubits have their polarization(horizontal, vertical, or diagnal) already entangled. After that, they feed photonic qubit 1, 3, and 5 in polarizing beam splitter(PBS), an instrument that directing photons with the same polarization to one direction and those with different to the other, in the way described by the picture, creates more photonic qubits, which are already entangled. While the qubits on one side is utilized to achieve path entanglement, qubit 2, 4, and 6 on the other side are fed into another setup of instruments that create photonic qubits that have their OAM entantled. Next, By carefully preparing and controlling the photons in these three degrees of freedom, the team was able to encode multiple qubits in each photon. Specifically, each photon could carry multiple bits of quantum information across its polarization, OAM, and path states. At the end, to verify the entanglement of 18 qubits, the team performed quantum state tomography and other measurements to analyze the correlations between the qubits. These measurements confirmed the presence of entanglement across the 18 qubits, demonstrating the successful manipulation and control of the complex quantum states.

2.7. Topological Qubits and Anyons

The purpose this technique is developed is similar to modern communication encoding that resists error and noise that corrupt partial information. Topological cubits use anyons, a 2 dimensional particle. Anyons can be braided, and braided anyons’ quantum states only depend on the braiding paterns instead of any other types of information, following the basic properties of topological braiding[5].

These properties can filter local noices and decoherence. Since topological qubits are strongly error proved, the system can be easily upscaled.

3. Quantum Gates and Algorithms

The properties of superposition and entanglement empower qubits to transform in complex logic, which is the capability classical bits lack of. Comparing the simple logical statements that classical gates are able to receive and output, quantum gates, as mathematical operators, can handle matrices in Hilbert space.

Single qubit gates, exactly like what it is called, process 1 single qubit once a time. Pauli Gate that rotates a qubit’s X, Y, and Z axes on Bloch Sphere model is an example of this type of gates[6].

As mentioned above, Bodies in microscopic scale lose their uniqueness and behave as a whole, an integrated system, after interaction, which phenomenon is called quantum entanglement. Multi-qubit gates’ function is to enable entanglement among qubits to perform complex quantum computation.

3.1. CNOT Gate

A CNOT Gate operates on a 2-qubit-system. The 1^st qubit is the control qubit, and the 2^nd qubit is the target qubit. When the 1^st qubit’s input is | 0 > , the 2^nd qubit’s output does not change; while when the 1^st qubit’s input is | 1 >, the 2^nd qubit will be flipped, thus the output will be the opposite of the input. When the 1^st input is 1, the CNOT Gate flips the 2^nd [7]. Equation 4 below is the mathematical expression of input and output through CNOT Gates.

\( CNOT(|00 \gt )=|00 \gt \)

\( CNOT(|01 \gt )=|01 \gt \)

\( CNOT(|10 \gt )=|11 \gt \)

\( CNOT(|11 \gt )=|10 \gt \) (4)

Quantum gates can be expressed as operators. CNOT Gate as an operator matrix in Hilbert Space can be written as the matrix below:

\( CNOT = [\begin{matrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{matrix}] \) (5)

3.2. Toffoli Gate

A Toffoli Gate is like a more complex version’s CNOT Gate, except of it operates on a 3-qubit-system: the 1^st and the 2^nd qubits are the control qubits, and the 3^rd qubit is the target qubit. Comparing to a CNOT Gates, a Toffoli Gate only flips the target qubit when both input qubits are both | 1 > [8]. Table 1 is a truth table of how a Toffoli Gate process qubits.

Table 1. A truth table for Toffoli Gate. A toffoli gate works with 3 qubits that 2 of them are utilized as control qubits.

3.3. Quantum Algorithms

Quantum algorithms are designed for quantum computers, performing computations with quantum mechanics principles, significantly more efficient than classical computers. For example, integer factorization in large number is not only a great challenge in classical computation, but also a keystone of cryptography.

In classical computation, algorithms that factoring large integers, such as Pollard’s Rho Algorithm and Fermat’s Factorization Method relies on random guessing or loops[9], which require large amount of times to process numbers one by one. Nevertheless, quantum mechanics principles such as superposition provides tremendously faster methods to find the period of the factoring function, eventually significantly outperform any classical algorithm.

Many properties of classical computation vastly used will no longer be usable. For example, the difficulty large integer factorization is utilized on cryptography, including information security and cryptocurrency. However, when a well supported enough quantum algorithm comes out , it can easily crack these codes and destroy the exist security and banking system relying on classical computer’s limitation.

4. Errors and Solutions

While promising unprecedented theoretical computational power, quantum computation faces even more complex potential errors comparing to its classical counterpart. Understanding and addressing these errors is crucial for the development of reliable and scalable quantum computers. The main sources of quantum computation errors includes decoherence, quantum noise, and bugs caused by false operations.

4.1. Quantum Decoherence

Quantum decoherence occurs when a quantum system loses its quantum coherence, meaning the system's quantum state becomes entangled with its environment, causing the loss of superposition. This process results in the system behaving more classically and less quantum mechanically, which undermines the advantages of quantum computation[10].

For example, a qubit is prepared to be in the superposition described by \( |ψ \gt =α|0 \gt +β \) |1> might lose its coherence over time due to the interaction with the complex surrounding environment, losing their relationship and even entangling with some non-related particles. When this happen, the \( |0 \gt \) and the \( |1 \gt \) can no longer interfere with each other.

4.2. Quantum noises

Amplitude damping, also called relaxation, is the phenomenon that an excited state decays to a lower energy state, often resulting in energy loss. Even when a qubit’s energy state does not change, the loss of relative phase information between its phases is also a significant type of quantum noise[11]. For example, the qubit, expressed by equation 6, is in a superposition state, while it later loses the relative phase information between its 2 eigenstates and become equation 7.

\( \frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt ) \) (6)

\( \frac{1}{\sqrt[]{2}}(|0 \gt \lt 0|+|1 \gt \lt 1|) \) (7)

Noises can cause, for example, a qubit on | 0 > flipping to | 1 > or vice versa. This is called “bit flip”. Even if the state of the qubit is not changed, the relative phase between its states can be altered like equation 8. This is called “phase flip”.

\( \frac{1}{\sqrt[]{2}}(|0 \gt +|1 \gt →\frac{1}{\sqrt[]{2}}(|0 \gt -|1 \gt ) \) (8)

4.3. Some Error Correction Methods Under Development

As well as classical computation, when errors appear, mitigation and debugging is needed. Different from classical computation, one of the biggest challenges in microscopic scale is that the qubits in superposition will collapse to their eigenstates when measurement is made. Therefore, making direct measurement is a process that should be avoided as much as possible in purpose of error correction.

Instead of periodically taking measurement in the quantum system to diagnosis and correction methods the possible error(which is the traditional method), a new solution being developed is integrating the error diagnosis and correction into the system’s dynamic[12]. This method is called Autonomous Quantum Error Correction.

Three scientists, David Arvidsson-Shukur, Aiden McConnel, and Nicole Halpern, constructed a method that to amend the input state with a quantum teleportation circuit to simulate a worldline traveling backward to a certain point of time. This method allows the qubits to be measured instead of “affecting the measurement statistics”, which is the output[13].

Encoding the target classical bits into a more complex function set to prevent information loss or curruption is a method vastly used in many fields even include radio communication. Shor Code is one of the first quantum error prevention method developed. It encodes the target qubit into a block of 9 qubits[14].

5. Outlook of the Future Development

The future of qubits and quantum computation focuses on the enhancement of coherence, stability, scalability, and integration. When improvements in these areas are made, quantum algorithms made from communication, cryptography, and other fields will be practical. The next steps will be massive production and commercialization.

One of the primary goals in future development is to enhance the coherence times and stability of qubits. Current qubits are highly susceptible to decoherence and quantum noise, which limit their practical application. Advances in materials science and quantum control techniques are expected to produce qubits with longer coherence times and greater resistance to environmental disturbances. This will allow for more complex and extended quantum computations. Scalability remains a critical challenge in quantum computing. Future developments will focus on creating scalable quantum systems that can integrate a large number of qubits. Innovations in qubit interconnects, error correction protocols, and quantum network architectures will be crucial for building large-scale quantum computers.

Nevertheless, improving quantum error correction methods will be pivotal in the future of qubit development. Techniques such as surface codes, which offer high fault tolerance, are under active research. Autonomous quantum error correction, which integrates error diagnosis and correction into the system's dynamics without requiring direct measurement, is another promising approach. As error correction protocols become more efficient, the reliability of quantum computations will increase significantly.

6. Conclusion

Leveraging the unique principles of quantum mechanics such as superposition and entanglement, instead of like a new smart phone or other electronic products that are actually advances in small steps, the application of qubits is a great leap into the next generation, although people cannot see them in their laptops yet. Beyond the limitation of classical bits, qubits can exist in multiple states simultaneously, function as continuous variables comparing to classical binary systems. This paper aims to provide an integrated overview of the properties and applications of qubits. These researches of qubits underscores the transformative potential of quantum computation.

Throughout this article, the how single qubits coordinate and enable complex quantum computation is explained, and abstract math tools like Bloch Sphere are introduced. We explored various types of qubits. The development of qubits’ types satisfying different demands leads to the design of quantum gates and algorithms, illustrating the strong potential to solve problems intractable for classical computers. This article also discusses various error sources and correction methods, including decoherence, quantum noise, and autonomous quantum error correction. Decoherence, caused by a quantum system's interaction with its environment, results in the loss of quantum coherence and the system behaving more classically. Quantum noise, such as amplitude damping and phase flip, further complicates the reliable operation of quantum computers. Autonomous Quantum Error Correction, for example, aims to integrate error diagnosis and correction into the system's dynamics without the need for direct measurement, which can disrupt the quantum state.

All in all, while quantum computation holds immense potential, realizing its full capabilities requires overcoming significant technical challenges, particularly in error correction. Continued research and development in this field are essential for advancing quantum computation and unlocking its tremendous potential across various fields. The journey is just beginning, and the progress made so far is a testament to the collaborative efforts of researchers worldwide, paving the way for a future where quantum computation becomes a central pillar of technological advancement.