1 Introduction

As the Internet and computers are rapidly developing, the requirements for the security of computer networks have been increasing. The Rivest-Shamir-Adleman (RSA) algorithm is based on large prime factorization and the Digital Signature Algorithm (DSA) algorithm is based on discrete logarithm problems widely used in various security protocols and systems. However, these algorithms are no longer sufficient to meet the security requirements of computer networks. Therefore, it is particularly important to study elliptic curve cryptography with higher security under the same security level. In addition, high efficiency is also a major advantage of elliptic curve cryptography. In today's massive need for encryption or signature, various cryptographic encryption algorithms are widely used, and the problem of key storage comes with it. Elliptic curve cryptography uses a shorter key and studies show that the 160-bit elliptic curve cryptography algorithm is as secure as the 1024-bit RSA [1].

In 1985, Neal Koblitz and Victor S. Miller made their first attempt at elliptic curve cryptography; In 1998, ISO/IEC established elliptic curve cipher as a digital signature standard. In 2000, elliptic curve cryptography was adopted as an IEEE standard [2].

Today, elliptic curve cryptography has become one of the most widely used and secure cryptography. It is quite significant in cryptography, cyberspace security, information security, and system security. Elliptic curve cryptography is used in digital signature technologies, such as the Elliptic Curve Digital Signature Algorithm (ECDSA), which is now widely used in a variety of situations that require digital signatures [3]. Elliptic curve cryptography has also been applied to key exchange protocols like Elliptic Curve Diffie-Hellman (ECDH), which enables users to distribute keys more securely [4]. Nowadays, with the development of blockchain, the role of elliptic curve cryptography is more obvious, for example, Bitcoin uses the ESDCA digital signature algorithm to ensure security. With the development of technology and the optimization of hardware and software, the implementation of Elliptic Curve Cryptography (ECC) has become more and more efficient.

However, elliptic curve cryptography still faces some problems. For example, despite the optimization, it is still unavoidably computationally huge. In addition to this, there is also the risk of quantum computing attacks, and according to Shor's algorithm, quantum computers can solve discrete logarithm problems on elliptic curves [5].

This paper will introduce elliptic curve cryptography from three aspects: theoretical basis, security analysis, and practical application cases so that readers can understand the basic principles of elliptic curve cryptography. In addition, this paper will make readers intuitively understand the importance of elliptic curve cryptography through security analysis and practical cases, lay a foundation for readers to study elliptic curve cryptography, and trigger some thinking.

2 Theoretical basis

In the field of computer science and cryptography, elliptic curves on finite fields are generally studied, and some basic concepts are first analyzed. Before introducing finite fields and elliptic curves, this article will first introduce the concept of groups. In abstract algebra, a group is a basic algebraic structure. A group is a set and a binary operation on that set satisfies the following four conditions. The first condition is closure: For any two elements in the set that define the group, the result of using the binary operation that defines the group is still one element in the set. The second condition is that the binding is satisfied: for any three elements \( a, b, c \) in the set:

\( (a*b)*c=a*(b*c)\ \ \ (1) \)

Where \( * \) is a binary operation that defines the group. The third condition is the existence of a unit element: there is an element \( e \) in the set that defines the group, such that for any element \( a \) in the set:

\( e*a=a*e=a\ \ \ (2) \)

This element \( e \) is called a unit element or unitary element. The fourth condition is the inverse: for each element \( a \) in the group, there is an element \( b \) , such that:

\( a*b=b*a=e\ \ \ (3) \)

This element \( b \) is called the inverse of \( a \) , which is usually denoted as \( a^{-1} \) . Based on the group, the definition of the abelian group can be given: the abelian group refers to the commutative law that satisfies the operation based on the constituent group, that is, for any two elements \( a \) and \( b \) in the abelian group.

\( a*b=b*a\ \ \ (4) \)

The following describes the definition of a domain, which is a set of two binary operations, often referred to as addition and multiplication. For a set \( F \) and two binary operations \( + \) and \( * \) , \( ( F,+,*) \) is a domain if the following conditions are met: the elements in the domain and the \( + \) operation can form an abelian group, which is called an addition group. The elements in the set after removing the zero element ( \( 0 \) ) need to be able to form an abelian group, which is called a multiplicative group. In addition to this, the distributive property needs to be satisfied between the addition and multiplication groups: for any three elements \( a \) , \( b \) , and \( c \) in the domain.

\( a*(b+c)=(a*b)+(a*c)\ \ \ (5) \)

Based on a domain, if the number of elements in the domain is limited, the domain is called a finite domain. In addition, the feature is also an important concept of the domain, and the feature \( p \) of the finite field is a prime number, which represents the cyclic property of the elements in the domain under the addition operation, that is, for any element \( a \) in the finite field.

\( p*a=o\ \ \ (6) \)

Another concept in a finite field is order, and the order \( q \) of a finite field is the number of elements in that domain. For finite fields, the order \( q \) is a power of a prime number \( p \) .

\( q=p^{n}\ \ \ (7) \)

Where \( n \) is a positive integer.

The domain can be used as a carrier for elliptic curves, and the definition of elliptic curves is given below: Elliptic curves on the domain, the field of real numbers, the field of complex numbers, and the finite field are described by a non-singular algebraic equation, the standard form of which is the Weierstrass form:

\( y^{2}=x^{3}+ax+b\ \ \ (8) \)

Where \( a \) and \( b \) are constants in the domain need to meet the following non-singular conditions

\( 4a^{3}+27b^{2}≠0\ \ \ (9) \)

This condition ensures that the curve is free from self-intersections or singularities. The image of an elliptic curve over a real field forms a smooth curve, where point \( P \) on the elliptic curve represents all ordered pairs \( (x,y) \) satisfying the elliptic curve equation. Additionally, there is a special point known as the infinity point \( O \) , sometimes referred to as the zero point, which lies on the elliptic curve in the projective plane. Its significance becomes evident in the addition rule. he addition rules for elliptic curves over the field of real numbers are defined as follows: Let \( P \) be a elliptic curve point, \( Q \) another elliptic curve point, and \( l \) be the straight line passing through \( P \) and \( Q \) , intersecting the curve at another point \( G \) , since the elliptic curve is symmetrical to the \( x-axis \) , the symmetry point \( R \) in relation to the \( x-axis \) of \( G \) is also on the curve, and \( R \) is defined as the result of \( P+Q \) , in particular, when \( P \) and \( Q \) are the same point, it can be found that l and tangent are defined as the same, That is, \( G \) is the tangent of the elliptic curve at the point \( P(Q) \) and the other intersection point of the elliptic curve. The addition of finite fields follows the graphical idea of real number fields, and the specific calculation rules are defined as follows::

\( If P≠Q,λ=\frac{Y_{q}-Y_{p}}{X_{q}-X_{P}} mod p\ \ \ (10) \)

\( If P=Q,λ=\frac{3X_{p}^{2}+a}{2Y_{p}} mod p\ \ \ (11) \)

\( X_{r}=λ^{2}-X_{p}-X_{q} mod p\ \ \ (12) \)

\( Y_{r}=λ(X_{p}-X_{r})-Y_{p} mod p\ \ \ (13) \)

\( O+O=O\ \ \ (14) \)

\( P+O=P\ \ \ (15) \)

\( P+(-P)=O\ \ \ (16) \)

Where \( λ \) is the slope of the line connected by \( PQ \) , in particular, when \( P=Q \) , \( λ \) represents the slope of the tangent at that point. \( X \) and \( Y \) denote the x-coordinate and y-coordinate, while the subscript represents the point, and the fraction represents the inverse operation. After getting the formula for calculating the addition, the multiplier rule can be derived, for example:

\( 2P=P+P\ \ \ (17) \)

3 Security analysis

The strength of ECC relies on the complexity of the elliptic curve discrete logarithm problem (ECDLP), i Currently, no known polynomial-time algorithm can efficiently solve ECDLP. The complexity of known algorithms such as Pollard's rho in solving ECDLP is about \( O(n^{\frac{1}{2}}) \) ,where n is the size of a finite field [6]. This means that it will not be feasible to calculate the time it takes to unravel ECDLP for properly selected elliptic curves and domain parameters. In addition, as with other cryptosystems, key length is an important consideration for ECC security. Due to the difficulty of ECDLP, ECC can provide security comparable to traditional public key algorithms, including RSA and DSA, at short key lengths. For instance, a 256-bit ECC key offers approximately equivalent security to a 3072-bit RSA key. [7]. This results in significant performance benefits, including faster computing and fewer storage requirements.

There are a few things to keep in mind to further enhance security. The first is the selection of elliptic curves, not all elliptic curves are equally safe. It is necessary to select a standard curve that has been rigorously analyzed and validated, such as the curves P-256 and P-384 recommended by the National Institute of Standards and Technology (NIST) or the curve secp256k1 used by Bitcoin [8]. There may be known attack methods or weaknesses for some specific curves. In addition, to prevent side-channel attacks, the ECC implementation needs to use a constant-time algorithm to avoid leaking critical time information. A side-channel attack may infer key information by analyzing physical characteristics such as the timing of the encryption operation, electromagnetic leakage, power consumption, etc.

The security of ECC also relies on some existing algorithms, for example, ECC relies on a high-quality random number generator RNG to generate private and ephemeral keys. A fragile random number generator can lead to key compromise. For example, the Sony PS3 hack in 2010 was due to the use of an insecure random number generator [9]. In addition, the security management of keys is essential for any cryptosystem. ECC keys need to be properly generated, stored, and used to prevent unauthorized parties from obtaining them.

In addition to known threats and vulnerabilities, potential threats are also worth considering. While there is currently no known effective attack capable of breaching the security of ECC, cryptography research is constantly advancing. The emergence of new attack methods can affect the long-term security of ECC. Especially concerning the possible impact of quantum computing, such as Shor's algorithm, which can efficiently solve problems like integer factorization and discrete logarithms. If a practical quantum computer emerges, existing ECCs will not be able to defend against such attacks. Therefore, researchers are developing quantum-resistant cryptography systems to replace existing public-key cryptography schemes. ECC is widely used in scenarios such as TLS/SSL, digital signatures (such as ECDSA), and key exchange (such as ECDH). Its safety has been proven in real-world applications, but it also needs to be constantly reviewed and improved. It is also important to follow the latest security standards and best practices when developing and deploying ECC.

4 Practical example

SM2 is a public-key cryptography algorithm standard based on elliptic curves, developed by the State Cryptography Administration of China (SCA), relying on the discrete logarithm problem of elliptic curves. The core part of the SM2 encryption algorithm is the encryption and decryption process, which is shown below, and two flowcharts are drawn in this paper, Figure 1 and Figure 2 make it more intuitive: Encryption process (Figure 1):

\( A1 \) :Generate random number \( k∈[1,n-1] \) ;

\( A2 \) :Calculate \( C1=[k]G=(x1,y1) \) ;

\( A3 \) :Calculate \( S=[h]PB \) ;

\( A4 \) :Calculate \( [k]PB=(x2,y2) \) ;

\( A5 \) :Calculate \( t=KDF(x2 || y2, klen) \) ;

\( A6 \) :Calculate \( C2 = M ⊕ t \) ;

\( A7 \) :Calculate \( C3 = Hash(x2 || M || y2) \) ;

\( A8 \) :Output ciphertext \( C = C1 || C2 || C3 \) .

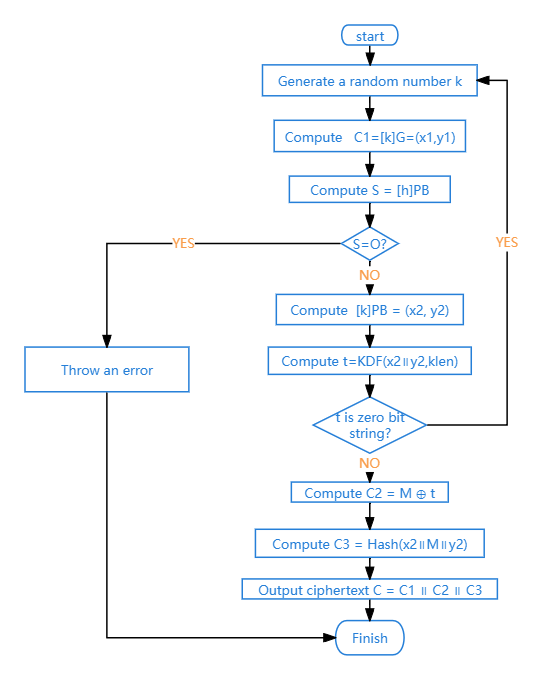
Figure 1. Flowchart of encryption (Original)

Decryption process (Figure 2):

\( B1 \) :Extract \( C1 \) from \( C \) ;

\( B2 \) :Calculate \( S=[h]C1 \) ;

\( B3 \) :Calculate \( [dB]C1=(x2,y2) \) ;

\( B4 \) :Calculate \( t=KDF(x2 || y2, klen) \) ;

\( B5 \) :Extract \( C2 \) from \( C \) and calculate \( M \prime = C2 ⊕ t \) ;

B6:Calculate \( u = Hash(x2 || M \prime || y2) \) , extract \( C3 \) from \( C \) ;

B7:Output plaintext \( M \prime \) [10].

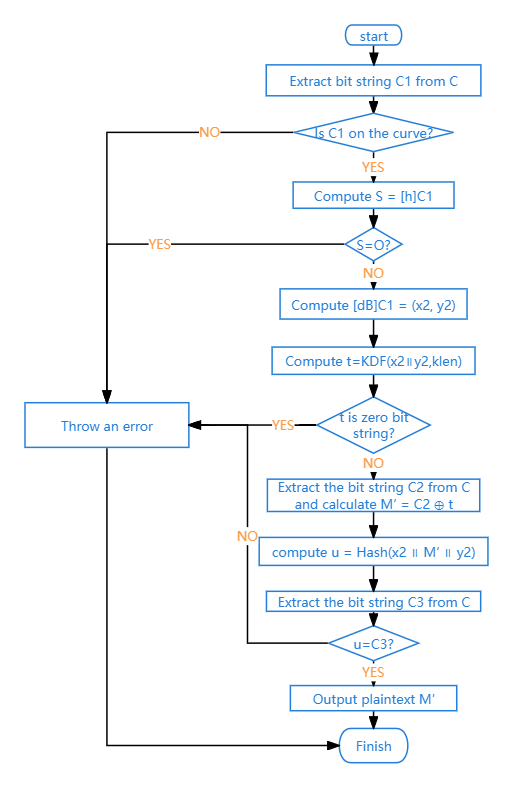
Figure 2. Flowchart of decryption (Original)

5 Conclusion

This paper deeply discusses the theoretical basis, security analysis, and practical application cases of Elliptic Curve Cryptography (ECC), and draws several important conclusions. First of all, ECC has become an important branch of cryptography due to its short key length and high security, especially in modern computer network environments that require high efficiency and security. Second, despite the potential threats such as quantum computing attacks, ECC has shown strong security and efficiency in real-world applications. In addition, ECC implementation has become more and more efficient, thanks to continuous optimization of hardware and software.

ECC is used in various applications, including digital signature technology, key exchange protocols, and blockchain technology, such as Bitcoin, which relies on ECC for security. These applications demonstrate the important role of ECC in securing online transactions and communications.

As technology advances and new threats arise, research in ECC will continue to develop and adapt. Especially in the context of the upcoming era of quantum computing, the research on the security of ECC and the development of quantum-resistant cryptography will be of great significance to ensure that the digital world can withstand potential security threats in the future.