1. Introduction
Robotic arms are widely employed in the military, manufacturing, medical, and other industries that involve high levels of risk. Research on trajectory-tracking technology for robotic arms has been significant. Accomplishing complex tasks in a robotic system relies heavily on accurately following predetermined joint trajectories. However, the robotic arm encounters difficulties in precisely and rapidly following the intended path because of uncertainties in the dynamics model, coupling effects, and unknown external disturbances. Therefore, it is crucial to examine a control method that is exceptionally effective.[1][2]The paper introduces a new control strategy for uncertain robotic manipulators with input saturation called "Reinforcement Learning-Based Fixed-Time Trajectory Tracking Control". This control law combines the principles of reinforcement learning and neural networks. The paper improves the attainment of fixed-time convergence of the system state by incorporating conventional robust control techniques. This results in notable advancements in the management of robotic systems, taking into account practical constraints.[3][4][5][6]The article focuses on developing a control design that accurately follows a pre-defined path for a robotic arm. The dynamics of the arm are unpredictable, and it is also prone to input saturation. The technique employs a recently created reinforcement learning algorithm that relies on radial basis function neural networks. It specifically employs advanced non-singular fast terminal sliding mode control to achieve the convergence of errors within a predetermined time period. Furthermore, it includes a nonlinear anti-jitter compensator that effectively handles actuator saturation.[7][8]The article centers around the difficulty of maneuvering through unknown surroundings in the field of robotics. Robotic arms are essential in a wide range of applications, especially in dangerous environments where precise control is required despite uncertainties in the system and external disturbances.[9]This study examines the interrelated issues of tracking and saturation, which are important for improving the performance and reliability of robots in real-world environments. This ensures that the convergence time is not influenced by the initial state of the system; in technical terms, it introduces the advantage of fast convergence times.[10]The control strategy outlined in the article improves the efficiency and feasibility of robotic systems in real-life situations by tackling the difficulties associated with trajectory tracking accuracy and actuator saturation resistance. This would mainly be applicable to robotics applications, and a flexible framework that integrates machine learning could have broader applicability. While the main focus is on robotic arms, these methodologies and discoveries have the potential to be applied to other dynamic systems facing similar challenges, thereby broadening the impact of the research. For example, it is essential to incorporate pursuit and dimensional stability control in complex environments that are defined by second-order arithmetic control equations.
2. Formatting the title, authors and affiliations
To gain an intuitive understanding of the control law concept, we initially isolate the neural network (NN) to examine the overarching control law.
2.1. Control law without neural networks
\( τ=-\frac{1}{{v_{1}}}({K_{tiled}}+K)\cdot sig({e_{2}},2-{v_{1}})+ddxd-{d_{max}}\cdot sig(s) \) (1)
The control law, which does not incorporate neural networks (NNs), solely depends on traditional control techniques, such as PD control (proportional-differential control). The values of the gains \( K \) and \( {K_{tiled}} \) are determined by an error-based adaptive gain matrix. The effectiveness of the control law is highly dependent on the designer's ability to determine and fine-tune these gains, as well as potentially other parameters, in order to achieve desirable control performance. Neural networks may not be well-suited for unknown or changing dynamic environments due to their limited self-learning and adaptation capabilities.
2.2. Implementation of control laws for neural networks
\( τ=-\frac{1}{{v_{1}}}({K_{tiled}}+K)\cdot sig({e_{2}},2-{v_{1}})-\frac{1}{{v_{1}}}\cdot {|e2|^{(1-v1)}}\cdot \) \( (sig(({σ_{1}}\cdot sig(s,v2)+{σ_{2}}\cdot sig(s,v3)),v4)+ζ+{K_{s}}\cdot s) \) \( +ddxd-fnn-{d_{max}}\cdot sig(s) \) (2)
The incorporation of NN neural networks introduces a self-learning aspect ( \( fnn \) stands for Feedforward Neural Network, which is used to anticipate future events. \( zeta \) refers to the integration component of a system, which is responsible for correcting persistent deviations) to the control law. The control behavior relies on the prognostication of the actuator neural network, while the integral component aids in rectifying persistent deviations. This adaptive mechanism enables the control system to acquire knowledge and adapt to disturbances, while maximizing performance in a perpetually evolving dynamic environment. The neural network has the ability to dynamically adjust its weights in real-time while performing control tasks, thereby improving the accuracy of trajectory tracking and the overall stability of the system.
2.3. Consequences and Distinctions
Within the control law, the gain matrices \( K \) and \( {K_{tiled}} \) can be either fixed or adaptively adjusted using heuristic rules, without the inclusion of neural networks. However, these adjustments are typically pre-designed and do not rely on real-time feedback of system performance. The control law implemented in the neural network calculates the gain in real-time. The effect of weights, specifically in the context of the output of the Actor's neural network, is to either replace or enhance a portion of the conventional control law, thereby serving as a control action that is dynamically adjusted. In the absence of neural networks (NN), this specific aspect of the control action may require prior calculation or be determined by alternative control logic. While optimizing the control actions using a learning process can enhance their adaptability to the specific behavior and dynamics of the system, the presence or implementation of the integral part or state variable may not be necessary in control laws that do not involve neural networks, or it can be achieved through alternative mechanisms. For instance, the integral component of PID control is commonly employed to eliminate steady-state errors. \( zeta \) updating is employed in control laws that incorporate neural networks to improve the adaptability and robustness of the controller, particularly when addressing persistent systematic deviations. The implementation of neural networks has an impact on the function of the gain matrix in traditional control laws. Neural networks offer an adjustable gain mechanism that can be customized to match the real-time performance of the system. They can respond more dynamically to changes in the system state compared to gains that are static or change slowly. By adopting this approach, the control strategy of the system gains enhanced flexibility and the ability to independently acquire the knowledge necessary to efficiently guide the system towards a desired trajectory.
|
| |
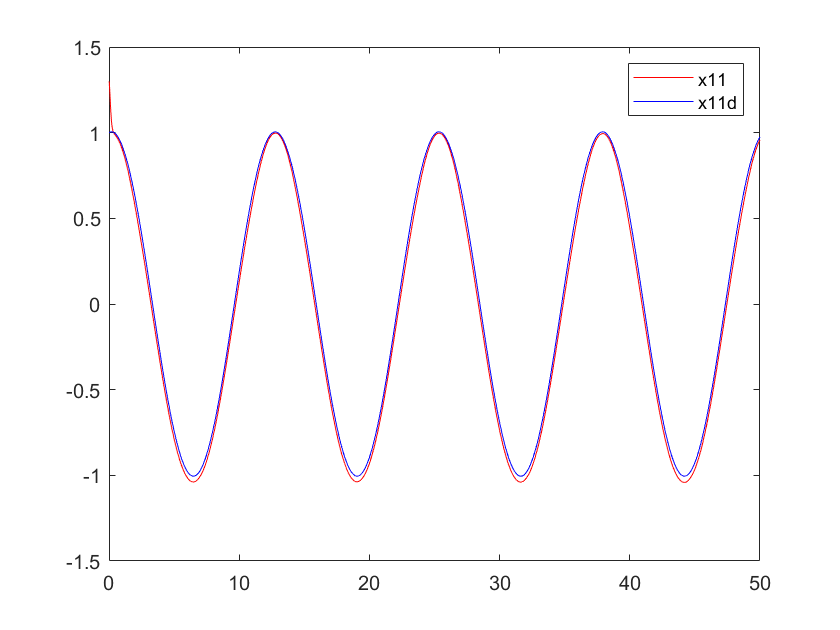
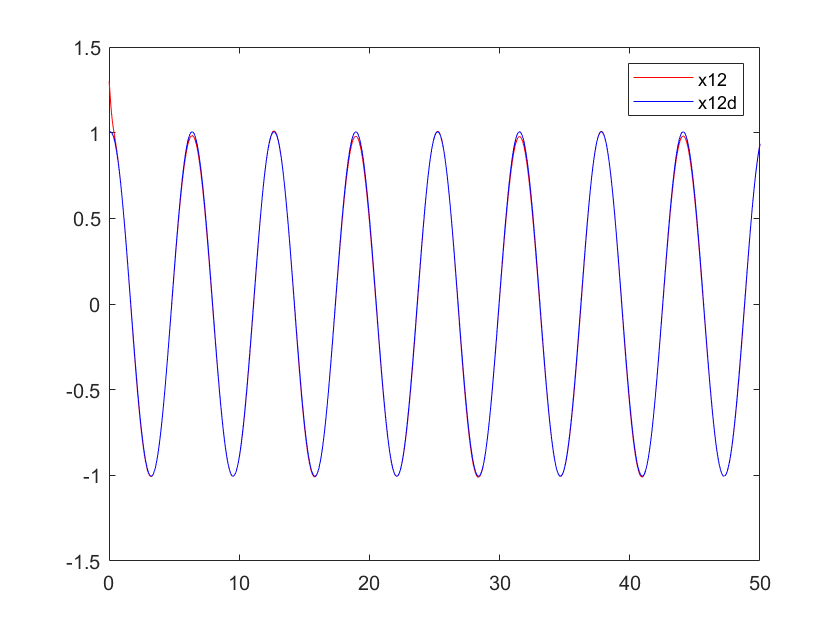
Figure 1. The position curve of arm 1 | Figure 2. The position curve of arm 2 | |
|
| |
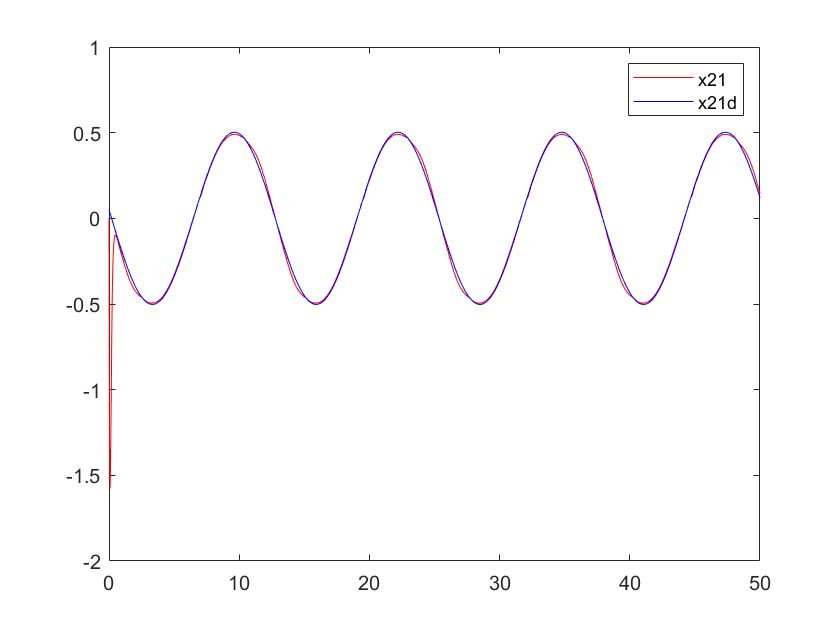
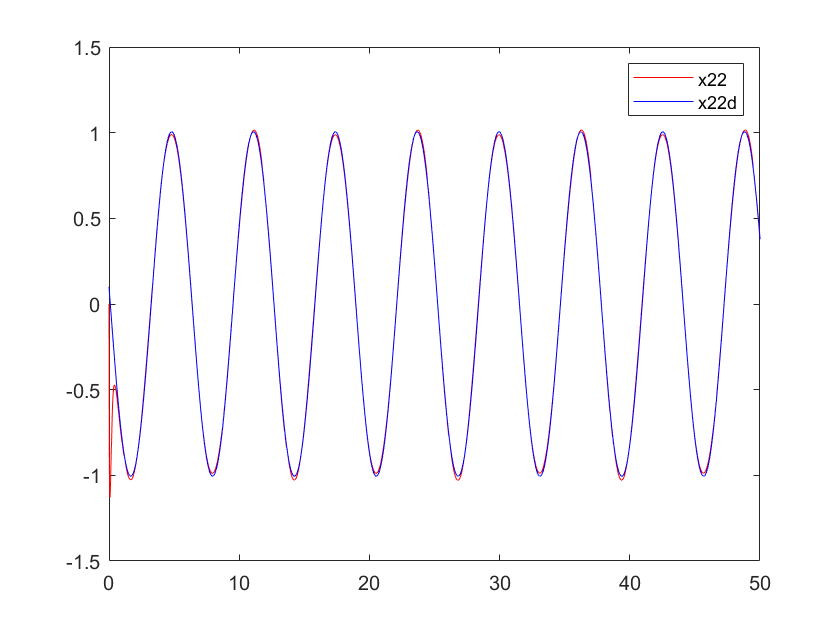
Figure 3. Velocity profile of arm 1 | Figure 4. Velocity profile of arm 1 | |
|
| |
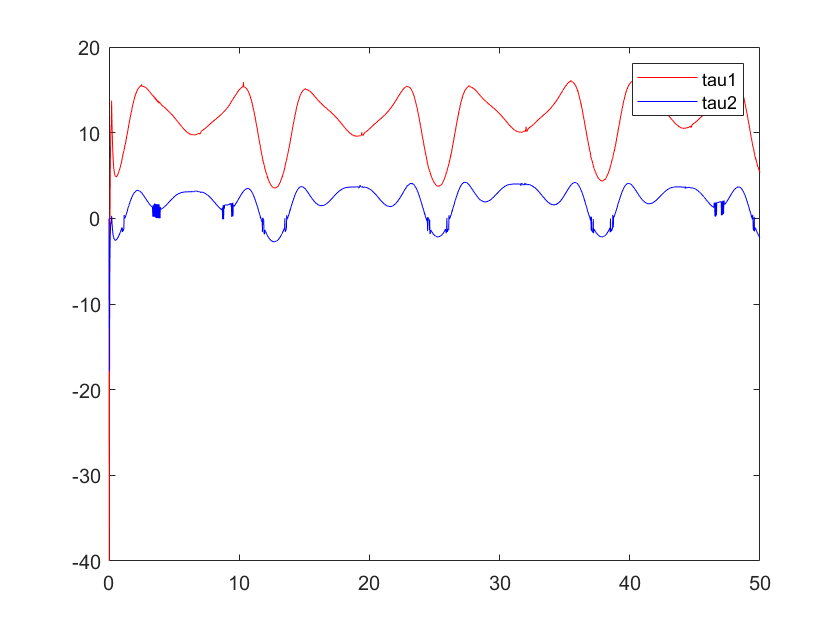
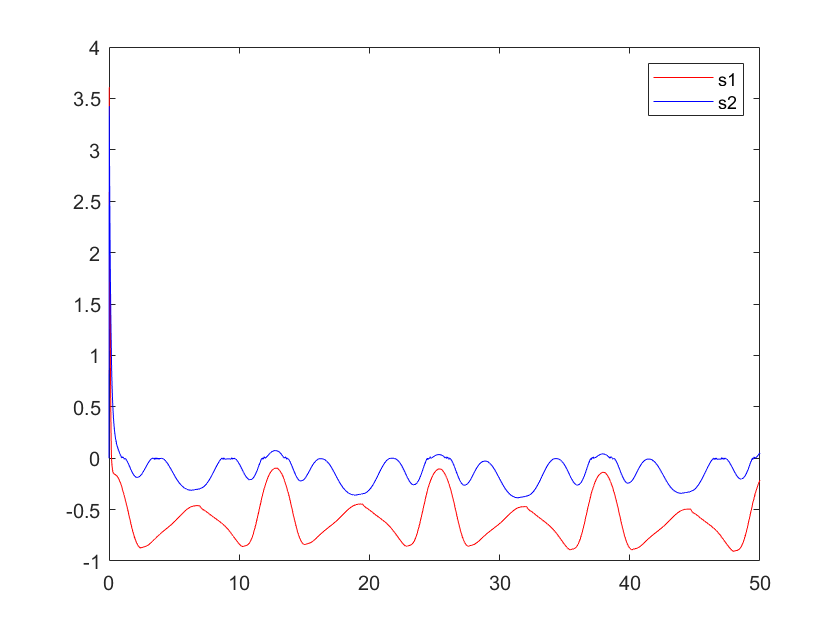
Figure 5. Input torque of control | Figure 6. State error vector (combination of position error and velocity error) |
3. Advancement
Given the advancing automation and robotics, the demand for precise and dependable robotic systems is growing significantly across different industries. Ensuring accurate trajectory control is crucial in various fields, such as advanced manufacturing and delicate surgical procedures, even in the presence of system uncertainties and external disturbances. The innovative study on "RL.etc" has achieved a significant advancement in trajectory tracking by integrating sophisticated reinforcement learning algorithms with robust control techniques. This breakthrough is crucial for applications that demand precise and efficient performance, serving a wide range of application scenarios.
There are still opportunities for enhancing this control algorithm, and while the current control strategy already incorporates reinforcement learning, it primarily depends on pre-learned strategies for decision-making. While it excels in numerous applications, there is still room for improvement in its capacity to learn and adapt to new situations in real-time. In order to accomplish this, incorporating online learning mechanisms or incremental learning strategies into the control framework would allow the system to consistently acquire new knowledge and adjust its behavioral strategies in real-time to adapt to ongoing environmental changes.
Another possible avenue for improvement is to augment the interpretability and transparency of the algorithms. Reinforcement learning algorithms, particularly those based on neural networks, are commonly perceived as "black boxes," which restricts their usage in specialized fields (such as healthcare or aviation) that demand stringent safety standards. Enhancing users' trust and understanding of the system's behavior can be achieved by developing algorithms that are more transparent or by visualizing the decision-making process.
Nevertheless, the primary focus is on enhancing the precision of the source data or transitioning from force-displacement fields to alternative fields in order to enhance accuracy and practicality, which is highly intriguing.
3.1. System Flexibility
Due to the intricate and dynamic nature of robot operating systems, it is often necessary for a single force-displacement field to encompass all relevant information about the environment. Incorporating data from additional physical domains, such as temperature and vibration, can enhance the overall understanding of the environmental operating conditions and enable the system to adapt more effectively. When operating in extreme temperature environments, temperature data can be used to regulate the robot's power output and prevent performance degradation caused by overheating or overcooling. However, irregular mechanical vibrations can be harnessed and regulated through electrical signals that are converted using the piezoelectric effect.
3.2. Enhanced Precision of Control Strategies
Modifying data resources can enhance the modeling and prediction of robot behavior, resulting in more precise control. The integration of multi-dimensional data enables the robot to effectively handle uncertainty, particularly in situations involving input saturation or other extreme operating conditions.
3.3. Enhancement of system robustness is achieved in section
Utilizing data from multiple sources enhances the system's resilience against individual sensor failure or data distortion. In the event of a force sensor malfunction, the system can rely on alternative sensor data, such as position, temperature, or vibration, to ensure operational stability and safety.
3.4. Broadening the Scope of Robot Applications
By incorporating diverse physical data, robotic operators can be employed in conventional industrial settings and extended to novel domains that demand sophisticated environmental perception, such as disaster response, deep-sea exploration, or operations in extreme weather conditions.
3.5. Encouraging the Collaboration of Different Academic Disciplines in Research
The integration of machine learning and control theory with research in physics, materials science, and other disciplines not only fosters the advancement of robotics, but also enables breakthroughs in these fields, drives the development of novel sensing technologies and materials, and further improves the performance and versatility of robots.
4. Conclusion
This study focuses on the implementation and optimization of a reinforcement learning-based fixed-time trajectory tracking control algorithm for robot arms with uncertain dynamics. Our methodology integrates commenter and actor neural networks to minimize tracking errors and achieve a resilient level of performance.
At first, we established a constant learning rate for updating the weights of the neural network. Nevertheless, the system exhibited subpar performance, characterized by notable variations in the control input tau and unpredictable error convergence. These problems indicate that the learning rate should be meticulously adjusted in order to achieve a balance between the speed of convergence and the stability of the system.
Through multiple iterations, we refined our control during the optimization process by making incremental adjustments to the learning rate. In the initial attempt, a high learning rate is established, resulting in noticeable oscillations and instability in the system. Consequently, we systematically decreased the learning rate with the expectation of attaining smoother and more stable control outcomes. After multiple iterations of fine-tuning, we ultimately selected a reduced learning rate, resulting in a notable enhancement in the system's ability to accurately follow trajectories. The control input tau exhibits enhanced smoothness, resulting in accelerated and more stable convergence of errors.
The findings highlight the crucial importance of accurately adjusting the learning rate in a reinforcement learning control system. By conducting multiple experiments and implementing optimization techniques, we have effectively enhanced the overall control performance of the system. As a result, we have achieved precise trajectory tracking even in uncertain and nonlinear environments.
Ultimately, through meticulous adjustment of the learning rate, we achieved substantial enhancements in both the stability and accuracy of trajectory tracking for robotic systems with uncertain characteristics. Subsequent studies could investigate more sophisticated optimization methods, such as incorporating the Adam optimizer, to further improve the system's performance.
References
[1]. Zuo, Z., Defoort, M., Tian, B., & Ding, Z. (2020). Distributed consensus observer for multiagent systems with high-order integrator dynamics.IEEE Transactions on Automatic Control, 65(4), 1771–1778. https://doi.org/10.1109/TAC.2019.2936555
[2]. Hirai, K., Hirose, M., Haikawa, Y., & Takenaka, T. (1998). The development of Honda humanoid robot.In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), 1321–1326, Leuven, Belgium: IEEE. https://doi.org/10.1109/ROBOT.1998.677288
[3]. Yang, C., Li, Z., Cui, R., & Xu, B. (2014). Neural network-based motion control of an underactuated wheeled inverted pendulum model.IEEE Transactions on Neural Networks and Learning Systems, 25(11), 2004–2016. https://doi.org/10.1109/TNNLS.2014.2302475
[4]. Zhang, P., Wu, Z., Dong, H., Tan, M., & Yu, J. (2020). Reaction-wheel-based roll stabilization for a robotic fish using neural network sliding mode control.IEEE/ASME Transactions on Mechatronics, 25(4), 1904–1911. https://doi.org/10.1109/TMECH.2020.2992038
[5]. He, W., Ge, S. S., Li, Y., Chew, E., & Ng, Y. S. (2015). Neural network control of a rehabilitation robot by state and output feedback.Journal of Intelligent & Robotic Systems, 80(1), 15–31. https://doi.org/10.1007/s10846-014-0150-6
[6]. Yang, C., Jiang, Y., Li, Z., He, W., & Su, C.-Y. (2017). Neural control of bimanual robots with guaranteed global stability and motion precision.IEEE Transactions on Industrial Informatics, 13(3), 1162–1171. https://doi.org/10.1109/TII.2016.2612646
[7]. Sun, L., & Liu, Y. (2020). Extended state observer augmented finite-time trajectory tracking control of uncertain mechanical systems.Mechanical Systems and Signal Processing, 139, 106374. https://doi.org/10.1016/j.ymssp.2019.106374
[8]. Zhao, L., Zhang, B., Yang, H., & Wang, Y. (2017). Finite-time tracking control for pneumatic servo system via extended state observer.IET Control Theory & Applications, 11(16), 2808–2816. https://doi.org/10.1049/iet-cta.2017.0327
[9]. Cao, S., Sun, L., Jiang, J., & Zuo, Z. (2023). Reinforcement learning-based fixed-time trajectory tracking control for uncertain robotic manipulators with input saturation.IEEE Transactions on Neural Networks and Learning Systems, 34(8), 4584–4595. https://doi.org/10.1109/TNNLS.2021.3116713
[10]. Bhat, S. P., & Bernstein, D. S. (2000). Finite-time stability of continuous autonomous systems.SIAM Journal on Control and Optimization, 38(3), 751–766. https://doi.org/10.1137/S0363012997321358
Cite this article
Zhang,Z. (2024). Reproduction and generalization of robot trajectory tracking control method using reinforcement learning and neural network techniques. Theoretical and Natural Science,56,19-24.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 2nd International Conference on Applied Physics and Mathematical Modeling
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Zuo, Z., Defoort, M., Tian, B., & Ding, Z. (2020). Distributed consensus observer for multiagent systems with high-order integrator dynamics.IEEE Transactions on Automatic Control, 65(4), 1771–1778. https://doi.org/10.1109/TAC.2019.2936555
[2]. Hirai, K., Hirose, M., Haikawa, Y., & Takenaka, T. (1998). The development of Honda humanoid robot.In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), 1321–1326, Leuven, Belgium: IEEE. https://doi.org/10.1109/ROBOT.1998.677288
[3]. Yang, C., Li, Z., Cui, R., & Xu, B. (2014). Neural network-based motion control of an underactuated wheeled inverted pendulum model.IEEE Transactions on Neural Networks and Learning Systems, 25(11), 2004–2016. https://doi.org/10.1109/TNNLS.2014.2302475
[4]. Zhang, P., Wu, Z., Dong, H., Tan, M., & Yu, J. (2020). Reaction-wheel-based roll stabilization for a robotic fish using neural network sliding mode control.IEEE/ASME Transactions on Mechatronics, 25(4), 1904–1911. https://doi.org/10.1109/TMECH.2020.2992038
[5]. He, W., Ge, S. S., Li, Y., Chew, E., & Ng, Y. S. (2015). Neural network control of a rehabilitation robot by state and output feedback.Journal of Intelligent & Robotic Systems, 80(1), 15–31. https://doi.org/10.1007/s10846-014-0150-6
[6]. Yang, C., Jiang, Y., Li, Z., He, W., & Su, C.-Y. (2017). Neural control of bimanual robots with guaranteed global stability and motion precision.IEEE Transactions on Industrial Informatics, 13(3), 1162–1171. https://doi.org/10.1109/TII.2016.2612646
[7]. Sun, L., & Liu, Y. (2020). Extended state observer augmented finite-time trajectory tracking control of uncertain mechanical systems.Mechanical Systems and Signal Processing, 139, 106374. https://doi.org/10.1016/j.ymssp.2019.106374
[8]. Zhao, L., Zhang, B., Yang, H., & Wang, Y. (2017). Finite-time tracking control for pneumatic servo system via extended state observer.IET Control Theory & Applications, 11(16), 2808–2816. https://doi.org/10.1049/iet-cta.2017.0327
[9]. Cao, S., Sun, L., Jiang, J., & Zuo, Z. (2023). Reinforcement learning-based fixed-time trajectory tracking control for uncertain robotic manipulators with input saturation.IEEE Transactions on Neural Networks and Learning Systems, 34(8), 4584–4595. https://doi.org/10.1109/TNNLS.2021.3116713
[10]. Bhat, S. P., & Bernstein, D. S. (2000). Finite-time stability of continuous autonomous systems.SIAM Journal on Control and Optimization, 38(3), 751–766. https://doi.org/10.1137/S0363012997321358